概率统计解答题经典例题突破
2018-03-08河南省新蔡县第一高级中学
■河南省新蔡县第一高级中学 陈 宏
概率统计是历年高考的热点内容之一,考查方式多样,选择题、填空题、解答题中都可能出现,而解答题常以考查离散型随机变量的分布列、均值为主。现将概率统计解答题中常考题型归纳如下,希望对同学们备战高考有所帮助。
一、以超几何分布与二项分布为背景的离散型随机变量的分布列、均值
例1 继微信支付对提现收费后,支付宝也开始对提现收费,随着这两大目前用户使用黏度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取2 0 0人,把这2 0 0人分为3类:认为使用支付宝方便,仍使用支付宝提现的用户称为“A类用户”;根据提现的多少确定是否使用支付宝的用户称为“B类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“C类用户”。A类用户1 2 0人,B类用户6 0人,C类用户2 0人。
(1)从这2 0 0人中按A类用户、B类用户、C类用户进行分层抽样,从中抽取1 0人,再从这1 0人中随机抽取4人,求在这4人中A类用户、B类用户、C类用户均存在的概率。
(2)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用X表示所选3人中A类用户的人数,求X的分布列与数学期望。
解题突破:(1)先利用分层抽样的特点分别求出A,B,C三类用户中应抽取的人数,然后运用排列组合求概率。(2)理解超几何分布与二项分布的区别和联系,二项分布是有放回抽取,超几何分布是无放回抽取。总体个数比起抽取次数来说非常大的时候,就可以近似按照二项分布的独立重复试验来计算。
解:(1)从这2 0 0人中按A类用户、B类用户、C类用户进行分层抽样,从中抽取1 0人,则A类用户6人、B类用户3人、C类用户1人。
设A类用户、B类用户、C类用户均存在的事件为事件D,则P(D)=
所以在这4人中A类用户、B类用户、C类用户均存在的概率为。
(2)把频率作为概率,从支付宝所有用户(人数很多)中抽取3人,可近似看作3次独立重复试验,所以X的所有可能取值为0,1,2,3,且

所以X的分布列为表1。

表1
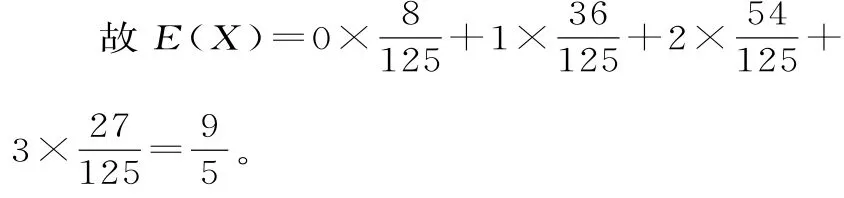
二、以茎叶图为背景的离散型随机变量的分布列、均值
例2 某市旅游节于2 0 1 7年5月1日举行,为了搞好接待工作,组委会在A大学和B大学中分别招募了8名和1 2名志愿者,将这2 0名志愿者的身高(单位:c m)绘制成如图1所示的茎叶图。若身高在1 7 5c m以上(包括1 7 5c m)定义为“高个子”,身高在1 7 5c m以下(不包括1 7 5c m)定义为“非高个子”,且只有B大学的“高个子”才能担任“兼职导游”。
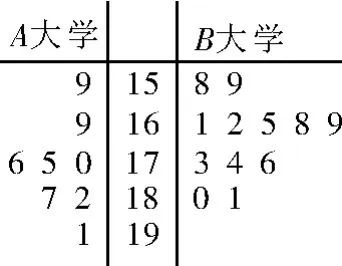
图1
(1)根据茎叶图指出B大学志愿者身高的中位数。
(2)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,那么至少有1人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用ξ表示所选志愿者中能担任“兼职导游”的人数,求随机变量ξ的分布列及数学期望。
解题突破:(1)利用茎叶图的知识求中位数;(2)利用超几何分布列出分布列。
(2)由茎叶图可知,“高个子”有8人,“非高个子”有1 2人,所以按照分层抽样抽取的5人中,“高个子”的人数为,“非高个子”的人数为,则至少有1人是“高个子”的概率为
(3)由茎叶图可知,A大学的“高个子”有5人,B大学的“高个子”有3人,则ξ的所有可能取值为0,1,2,3。

所以ξ的分布列为表2。

表2
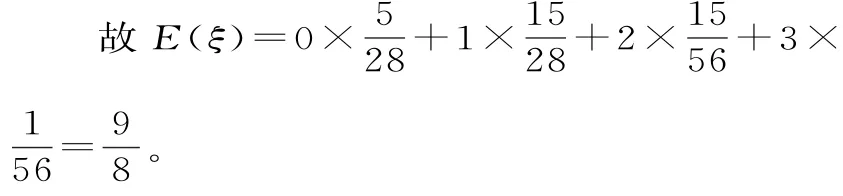
三、以频率分布直方图为背景的离散型随机变量的分布列、均值
例3 某校举行运动会,其中三级跳远的成绩在8.0m(四舍五入,精确到0.1m)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分,如图2所示。已知从左到右前5个小组的频率分别为0.0 4,0.1 0,0.1 4,0.2 8,0.3 0,第6小组的频数是7。
(1)求进入决赛的人数;
(2)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;

图2
(3)经过多次测试后发现,甲的成绩均匀分布在8~1 0m之间,乙的成绩均匀分布在9.5~1 0.5m之间,现甲、乙各跳一次,求甲比乙远的概率。
解题突破:(1)借助题设中的频率分布直方图以及频数和频率之间的关系求解;(2)运用二项分布公式求解;(3)运用几何概型公式求解。
解:(1)第6小组的频率为1-(0.0 4+0.1 0+0.1 4+0.2 8+0.3 0)=0.1 4,所以总人数为
所以第4,5,6组成绩均进入决赛,人数为(0.2 8+0.3 0+0.1 4)×5 0=3 6(人)。
所以进入决赛的人数为3 6。
(2)由题意知X的可能取值为0,1,2,进入决赛的概率为
所以X的分布列为表3。

表3
(3)设甲、乙各跳一次的成绩分别为x、y米。
记事件A为“甲比乙远的概率”,则基本事件满足的区域为x>y,如图3所示。
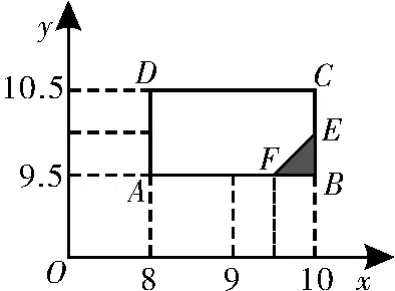
图3
四、以变量间的相关关系为背景的离散型随机变量的分布列、均值
例4 某厂有4台大型机器,在一个月中,1台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为。
(1)问该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障都能及时进行维修的概率不少于9 0%。
(2)已知1名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资。每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润。若该厂现有2名工人,求该厂每月获利的均值。
解题突破:(1)本题先识别为独立重复试验,其随机变量服从二项分布。(2)关键确定随机变量的取值:若至多2台机器出现故障,则获利4×5-2=1 8,若3台机器出现故障,则获利3×5-2=1 3,若4台机器出现故障,则获利2×5-2=8。
解:(1)1台机器运行是否出现故障可看作一次实验,在一次试验中,机器出现故障设为事件A,则事件A的概率为。该厂有4台机器就相当于4次独立重复试验,可设出现故障的机器台数为X,则

所以X的分布列为表4。

表4
设该厂有n名工人,则“每台机器在任何时刻同时出现故障都能及时进行维修”为X≤n,即X=0,X=1,X=2,…,X=n,这n+1个互斥事件的和事件,所以X的分布列为表5。

表5
(2)设该厂获利为Y万元,则Y的所有可能取值为1 8,1 3,8。
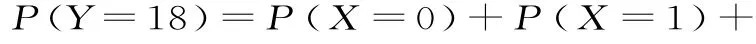

所以Y的分布列为表6。

表6
五、以独立性检验为背景的离散型随机变量的分布列、均值
例5 2 0 1 7年1月1日,作为贵阳市打造“千园之城”2 7个示范性公园之一的泉湖公园正式开园。元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放。现从到公园游览的市民中随机抽取了6 0名男生和4 0名女生共1 0 0人进行调查,统计出1 0 0名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图4所示。
(1)根据条件完成如表7所示的列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关。

图4

表7
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为,记甲通过的关数为X,求X的分布列和数学期望。
附:参考公式与数据(表8)。
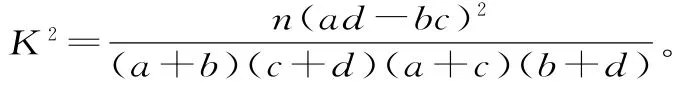

表8
解题突破:(1)利用公式计算K2,然后对照数据判断结论不成立。(2)先确定随机变量X的可能取值为0,1,2,然后求分布列。

表9
(2)记男生甲第i次通过第一关为Ai(i=1,2),第i次通过第二关为Bi(i=1,2),X的可能取值为0,1,2。
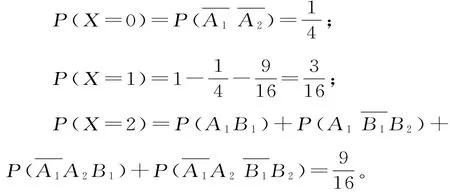
所以X的分布列为表1 0。
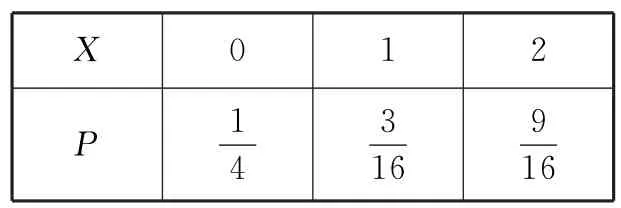
表10
