基于支持向量机的“拍照赚钱”任务打包与定价研究

戴靖宇+王姮冰+李乐吟

摘要：文章旨在对当前热门行业“拍照赚钱”的任务发布方案与定价方案进行研究。通过K-均值聚类模型和支持向量机，综合运用了MATLAB和SPSS等软件建立了相关模型，解决了在已有数据中挖掘定价规律，并以此为基础设计定价方案、任务打包发布方案。在对任务打包发布后，为了压缩成本，故通过一种合理且有效的方法，即折扣系数，修改定价方案。最终通过模拟我们发现新的打包发布方案和定价方案下的最终完成率大幅提升至92.22%，且总成本下降了3400元。

关键词：支持向量机；K-均值聚类多目标规划

一、研究背景

在劳动力价值不断高升的时代，如何利用社会的剩余劳动力，结合互联网思维，将原本需要专人完成的任务，通过互联网发布给大众共同完成，成为一个热点问题。

本文在现有任务单个发布定价方案和完成情况的数据中通过支持向量机挖掘任务定价与完成情况的规律，模拟不同定价下的完成情况，最后得到了一种在成本和完成率都较优的打包发布和定价方案。

二、模型的建立与求解

（一）通过K-均值聚类得到任务打包方案

由于任务点较为集中，故運用K-均值聚类算法对任务点进行打包。打包后我们发现部分包内任务量非常大，故又进行了二次拆包，由此获得了一个相对合理的任务打包方案。通过对任务进行打包最终设定200多个任务包。

具体过程如下：

1. 初始化

给定分类的个数，将835组任务点分为200组。同时置j=0，从样本向量中任意选定m个向量k，k，…，k作为聚类中心。

2. 样本归类

将每个样本向量x1=[xi1，xi2，…，x1n]T，即200个任务包，按照欧式距离计算公式归入中心为k的类别，欧氏距离公式为：

3. 中心调整

调整打包聚类中心，新的聚类中心K由以下式子计算得到，Ni表示聚类K

中的向量数，即：

k=（2）

4. 条件判断

构建迭代目标函数J，J=|xk-ki|，将中的数据代换入该式，判断J不再明显改变，即任务打包方案已经完善，此时迭代终止，否则j=j+1，重新进行。

最终成功打包835个任务为200多个任务包。部分结果如表1所示。

（二）多目标规划求解最优定折扣系数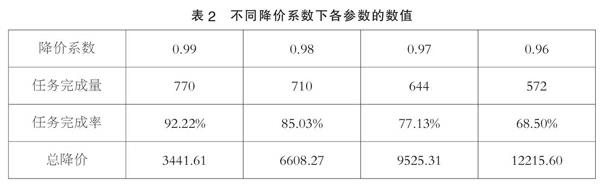

因为打包数量不同，其定价也不同，故设置了一个折扣系数，以期望降低总定价，即降低市场投入成本。随着打包数量n的不同，任务点定价为y·kn-1，其中y为原始定价。

不同的折扣系数k，对应的打包后的定价不同，相应的任务完成率也不同。对于公司而言，折扣系数越低对公司越有利。任务完成率越高，定价方案越好。此外会员能够接收预订任务限额不同。故以折扣系数最小、任务完成率最高为目标函数，会员的预定任务限额为约束条件，建立多目标规划模型：

目标函数：折扣系数最小、任务完成率最高为目标

其中，k为折扣系数，p为任务完成率。

约束条件：

由于打包后的任务个数不一样，且会员能够接收预订任务限额不同，故需要考虑打包后的任务会员能否领取任务。即约束条件为：

式中，Q表示在打包后距任务点3km内会员的个数，n表示打包后任务的个数。

综上所述，得到多目标规划模型如下：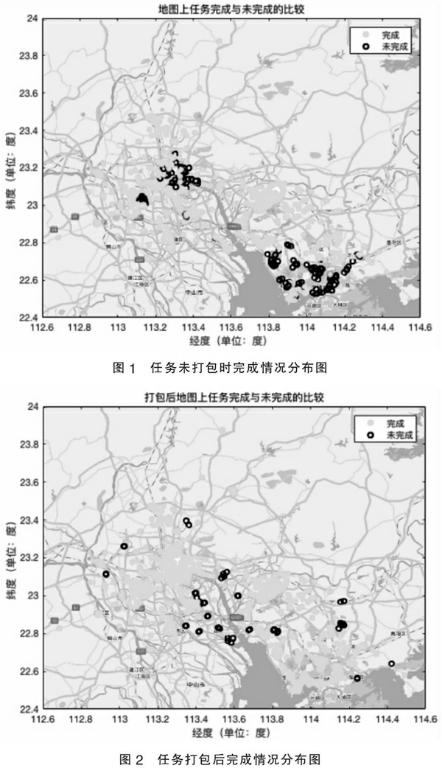

遍历不同折扣系数k的数值，利用支持向量机学习原始定价与完成情况的数据，模拟新定价下的完成情况。最终求得其对应的任务完成率。表2为求解得到的不同折扣系数下任务完成率的情况。

在降价系数为0.99，任务完成率为92.22%，总降价为3441.61，考虑公司的资金以及任务点完成率，选取降价系数为0.99作为新的定价方案。

（三）打包方案下的优化情况

在任务没有进行打包前，任务完成率为80%，将打包后完成率提升为92.22%。证明任务打包增加了任务完成率。利用MATLAB软件分别作图展示任务未打包和任务打包其任务点的完成分布情况，如图1、2所示。

三、结果分析

对比任务单独发布，任务打包有助于任务完成率的提高，效果最优可达到92%左右；.任务打包发布的最佳方案是200个包左右，其平均每包任务量为4到5；最优的折扣系数为0.99，可以节省成本超过3000元。

参考文献：

[1]司守奎，孙玺.数学建模算法与分析[J].国防工业出版社，2011（08）.

[2]宋天舒.空间众包环境下的3类对象在线任务分配[J].软件学报，2017（03）.

（作者单位：南京邮电大学）endprint