气象雷达风电场杂波抑制的匹配追踪算法

吴仁彪 丁 红 何炜琨 王晓亮 张 鑫

(中国民航大学天津市智能信号与图像处理重点实验室，天津 300300)

1 引言

随着化石能源不断耗尽，风能作为一种清洁环保、可再生的新能源呈现出最迅猛的发展势头，据全球风能理事会(Global Wind Energy Council， GWEC)报告显示，近十多年以来，全球风力发电累计装机容量呈现飞速增长趋势，2017年全球新增装机容量超过50 GW[1]。根据近五年数据预测，到2021年全球新增装机容量每年将达到75 GW左右的水平，到2021年底累计装机容量将达到800 GW[2]。我国风力资源极为丰富，风力发电很可能在今后能源产业中起到领军作用。然而，随着风电场规模在不断扩建，其产生的杂波影响了气象目标参数估计的准确性和稳健性，造成对雷雨风暴、湍流、风切变等恶劣天气的误识别和误判，对气象雷达系统性能带来愈发严重的影响。

关于气象雷达风电场杂波抑制问题，国外相关学者已关注多年。Kong Fanxing等人根据气象目标与风轮机的频谱特性差异利用自适应谱处理方法抑制风电场杂波[3]，该方法基于估计临近非污染区域的气象目标参数自适应地生成带通滤波器，滤除污染区域的风电场杂波，同时保留有用的气象信息。Nai Feng等人提出的距离多普勒自回归算法[4]则是首先检测出风电场杂波，用未受污染的数据来估计污染区数据，该方法是将抑制问题看成一个估计问题，而不是直接抑制污染区的风轮机杂波，这类方法的有效性依赖于未受污染的数据及其与污染区的欧式距离。Beauchamp R M等人利用雷达回波的时域相关性，将风轮机杂波近似为周期循环平稳过程，地杂波和气象目标近似为广义平稳过程，利用自适应滑动平均滤波器滤除风电场杂波[5]，该方法适用于凝式模式的气象雷达风轮机杂波抑制。2016年, faruk U.等人根据气象目标和风轮机在不同域中具有不同的稀疏性，采用信号分离理论从受污染的雷达回波数据中分离出风电场杂波实现杂波抑制[6]，实验中某些参数根据经验选取，算法较为复杂且在信噪比较低时抑制性能有限。国内关于风轮机杂波抑制，主要还是在航管监视雷达和沿海超高频雷达等方面研究，针对气象雷达风轮机杂波抑制我国目前研究相对较少，更多集中在风电场杂波检测及其对气象雷达的影响评估等方面研究[7- 8]。因此，在我国风能飞速发展的情况下，研究扫描模式的气象雷达风电场杂波抑制技术将有利于解决其对气象雷达的影响，降低拟建的气象观测设备及风电场的选址要求。

本文研究了气象雷达风电场杂波抑制的匹配追踪(Matching Pursuit， MP)算法。该方法首先需要构造超完备字典，往往规模较大的字典可以显著提高算法性能，但同时也会极大地增加存储量和计算量。为了解决这个问题，本文提出改进的匹配追踪算法，首先根据大地主题反解方法获得风轮机与雷达的相对距离和方位先验信息，提取出每个风轮机对应位置的雷达回波数据，从而可以降低待处理数据量及字典规模。实验结果表明，改进的匹配追踪算法在保证算法性能的前提下可以有效地降低计算量，提高运算效率。

2 数据模型

气象目标是由大量散射粒子组成，气象粒子在一定范围内作无规则运动，因而在某一频谱范围内会产生多普勒频移。理论研究和实验观测表明气象目标的功率谱可以近似为高斯分布[9-11]，相位谱服从[0，2π]上的均匀分布，结合功率谱和相位谱信息，并对其进行离散傅里叶逆变换，其对应的时域信号可以写为[9]

(1)

其中I、Q分别是雷达回波的同向通道和正交通道时域序列，Sk为功率谱，θk为相位谱，N为频域序列的长度。

风轮机信号模型主要是依据散射点叠加原理，远场条件下，可以将风轮机看作是一系列散射点叠加而成的几何体[12-13]。首先以风轮机的轮机舱为坐标中心，风轮机的旋转面为yoz平面，则x轴垂直于旋转面，如图1建立风轮机与气象雷达几何关系图。

图1 风轮机和气象雷达的几何关系图

图1中，φ为雷达视线(Line of Sight， LOS)与风轮机叶片夹角，β为雷达视线与z轴夹角的俯仰角，α为雷达视线在xoy平面上的投影与x轴的夹角，即雷达视线相对于垂直旋转面的方位角。P为风轮机叶片上任意散射点，lk表示轮机舱中心到风轮机叶片散射点P的距离，R和RP分别表示轮机舱中心和风轮机叶片散射点P到气象雷达的距离，由于(lk/R)2→0，所以RP近似为R-lkcosφ(t)，再去掉载波后，那么由散射点叠加理论可知风轮机三张叶片总的回波信号表达式为[13]

(2)

其中λ为雷达波长，设叶片长度为L，每个叶片有K个散射点，桅杆和轮机舱为静止目标，设有M个散射点，桅杆高度为H， hm为桅杆上散射点到雷达的距离，同样利用散射点叠加理论可得回波表达式[13]

(3)

最后整个风轮机的回波即为二者之和

sWT(t)=sblade(t)+smast(t)

(4)

对于气象雷达系统，接收到的气象雷达回波可以表示为

s=sWT+sweather+n

(5)

其中，sWT表示风轮机回波信号， sweather表示气象目标回波信号，n表示高斯白噪声。

3 传统匹配追踪算法

基于传统匹配追踪算法抑制气象雷达风电场杂波，就是从一组超完备字典中，找到若干个向量(也称为原子)尽可能的表示回波中的风轮机杂波。把气象雷达回波中最匹配原子所对应的成分从中减去，获得残余信号，然后对残余信号继续匹配，重复迭代，直到杂波残差值可以忽略为止。对应的流程图如图2所示。

依据传统匹配追踪算法，字典规模越大，原子越多，越有可能匹配到最合适原子，算法性能也就越好。然而每次匹配都需要做一次内积计算，字典规模越大，计算量和存储量自然就越大。当风轮机三个参数叶片转速frot、初始夹角θ0、方位角α步长设置较小时，构造字典总的原子数可达到上百万个，字典的建立及匹配过程运算量较大，在仅有四台风轮机的情况下就需要几个小时完成，随着风电场中风轮机个数的增加，运算量将呈现指数增长。为了解决这个问题，本文利用风轮机与雷达位置相关先验信息，基于大地主题坐标反解算法提取被风电场污染的回波数据，再利用传统匹配追踪方法抑制风轮机杂波，进而能够在保证该方法的良好抑制效果的前提下，能有效降低匹配原子的冗余度，提高运算效率和减少存储空间。

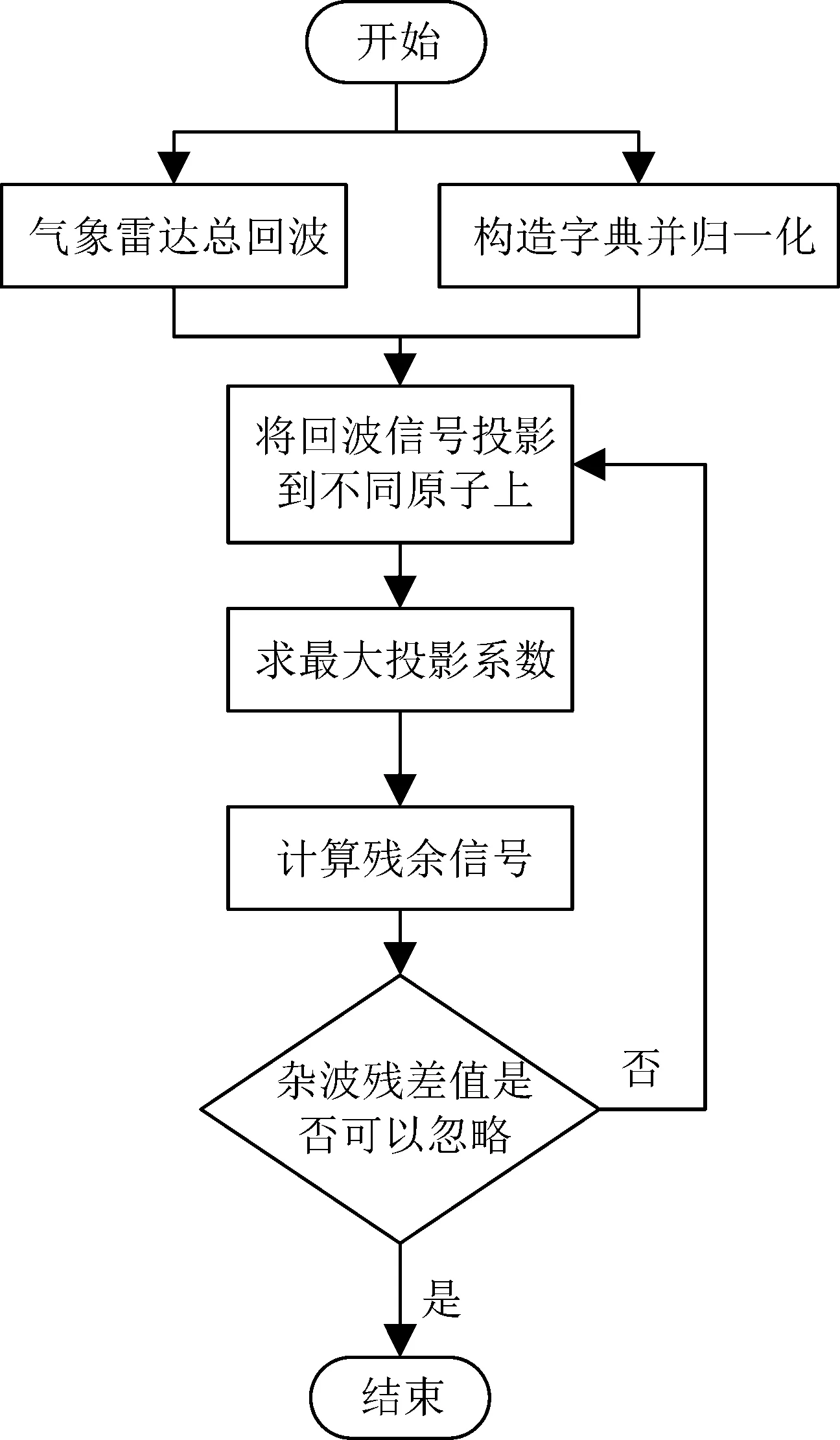
图2 传统匹配追踪算法流程图

4 改进的匹配追踪算法

为了降低传统匹配追踪算法计算量，利用风轮机距离和方位先验信息提取气象雷达回波中被污染的距离单元数据。本文首先通过谷歌地球读取雷达和风轮机所在位置的经纬度，利用白塞尔大地主题反解方法[15]获取到每个风轮机的精确距离和方位信息，白塞尔方法是解算方法中计算精度较高的一种，能够满足对距离和方位信息精度的要求。设气象雷达所在位置的经纬度分别为λ1、φ1，风轮机所在位置经纬度分别为λ2、φ2，λ为两点的经差。两点间的方位角可表示为[15]

(6)

两点的距离可表示为[15]

tanr=

(7)

由此可知，通过谷歌地球获取气象雷达和每个风轮机具体的经纬度，便可利用白塞尔大地主题反解方法求得其两者的距离和方位。

利用白塞尔大地主题反解算法获取气象雷达与风轮机之间精确的位置信息，从而可以提取受风电场污染的气象雷达回波数据，即利用距离信息确定风轮机所在距离单元，利用方位信息确定气象雷达扫描到风轮机时的相干脉冲回波数据。提取字典中有效数据，根据匹配追踪方法，将接收数据与字典原子进行匹配，即投影到不同原子上寻找最大投影值，确定最匹配原子并从回波数据中减去其所对应分量，计算残余信号，对残余信号继续匹配，同样进行反复迭代，直到风轮机杂波残差值可以忽略为止。算法流程图如图3所示。

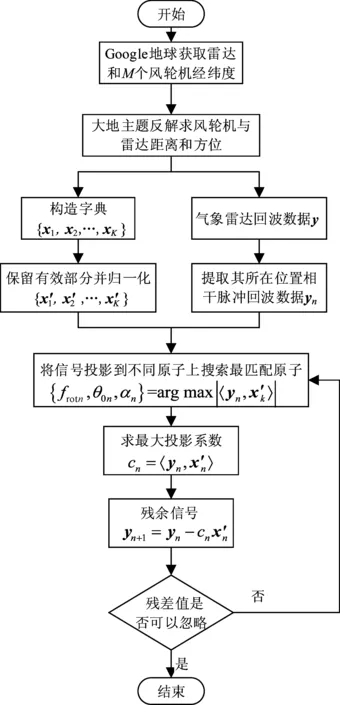
图3 改进后的风电场杂波抑制流程图

具体过程如下：

(1)在谷歌地球上，定位每台风轮机以及雷达所在位置，获取其经纬度信息。

(2)根据白塞尔大地主题坐标反解算法，计算每台风轮机相对雷达的距离和方位信息。

(3)根据距离和方位先验信息提取雷达回波中污染区数据。

(5)利用匹配追踪算法抑制风电场杂波，设迭代次数为n，依据先验信息，提取雷达回波中风轮机所在距离单元的相干脉冲回波yn，将该距离单元回波投影到字典中的不同原子上，每个原子对应的参数值不同，即

(8)

(9)

(7)求残余信号，从回波中减去该原子对应的分量即为残余信号

(10)

(8)用残余信号yn+1代替yn，从(5)重复该过程进行迭代，直到残余信号中风轮机杂波剩余量值足够小为止。依次处理M台风轮机所在距离单元的相干脉冲回波，直到所有风轮机杂波被抑制。

5 实验结果及性能分析

仿真实验中，气象目标参数、气象雷达参数及风轮机参数如表1～表3所示。

表1 气象目标参数

表2 气象雷达参数

表3 风轮机仿真参数

实际风电场具有几十甚至上百台风轮机，本实验考虑四台风轮机情况，相关参数如表4所示。

表4 四个风轮机参数

5.1 实验结果

为了模拟真实天气回波的功率谱，信噪比(SNR)一定的情况下，在气象目标中加入平均功率为1的加性高斯白噪声。如图4所示，只含有噪声的气象目标回波功率谱图和时频图可以看出，气象目标的频谱分布在一定的频谱范围内，具有一定的频谱扩展，其中心频率和谱宽由气象目标相对于气象雷达的平均径向速度以及速度谱宽所决定。

整个风电场的气象雷达回波如图5所示，图5(a)是气象雷达扫描范围的距离方位图，四台风轮机分布在相对气象雷达的不同距离和方位上，图中四个较亮的点就是四台风轮机所对应的位置，由图可以看出主要分布在方位30°～60°和距离20～30km之间。

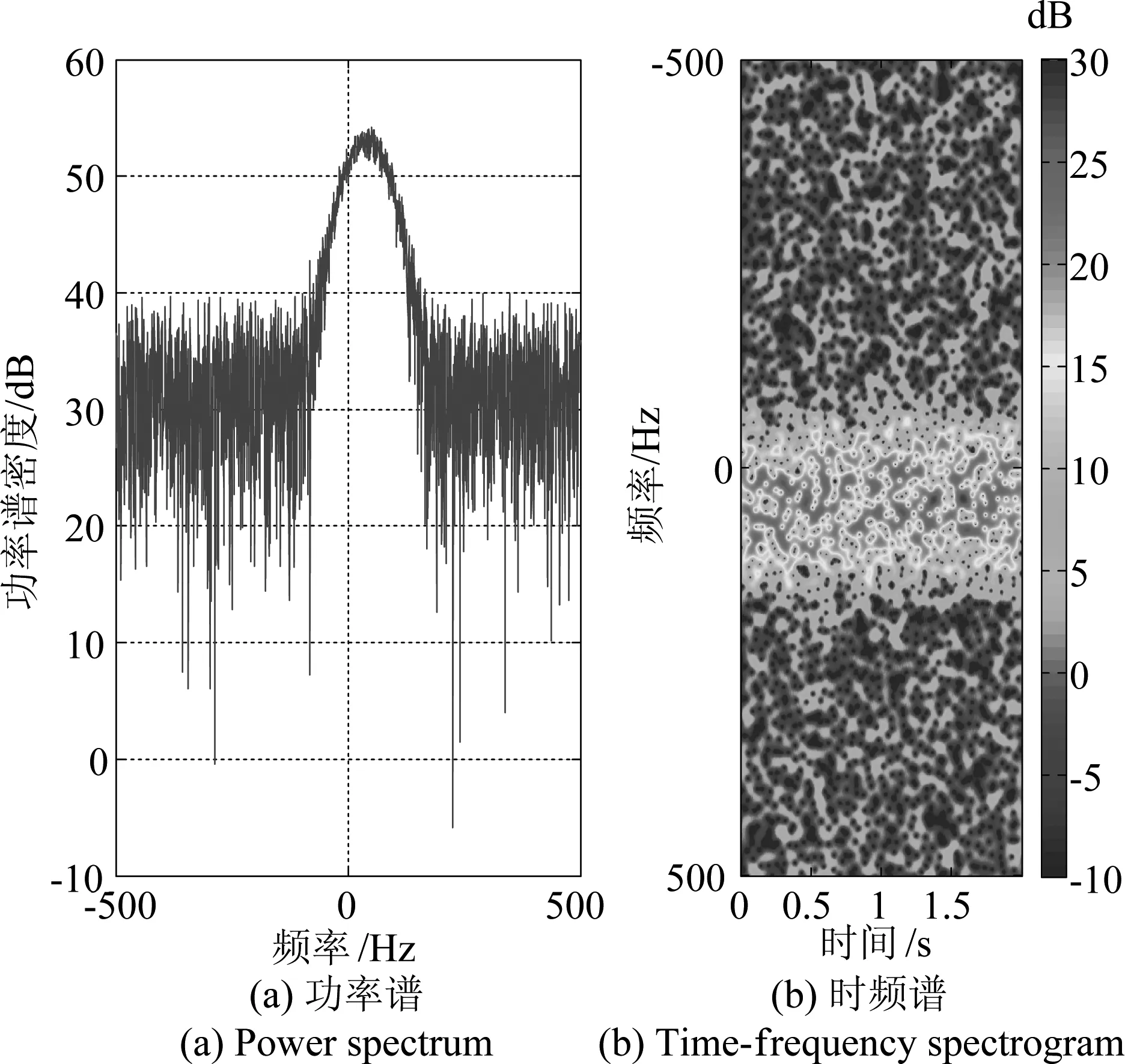
图4 含有噪声的气象目标回波

图5 气象雷达回波的距离方位和距离多普勒谱

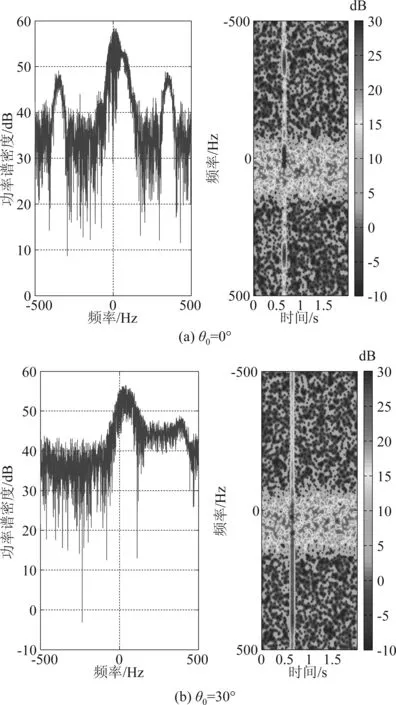
图6 不同初始夹角的气象雷达回波功率谱和时频谱

图5(b)是气象雷达扫描范围的距离多普勒，可以看出气象目标频谱具有随距离连续分布特性，另外四条明显的频谱是风轮机所对应的频谱。提取风电场中第四台风轮机所在距离单元的回波，其功率谱和时频谱如图6所示。叶片的初始夹角θ0不同，风轮机的频谱分布情况就不同。图6(a)当初始夹角为0°时，可以看出在零频处和正负频率处风轮机能量较强，零频处是参考叶片的回波能量，而另外两个叶片关于参考叶片对称，所以其频率也是对称分布。图6(b)初始夹角为30°时，由于雷达视线与参考叶片垂直，叶片上所有的点到气象雷达距离相同，回波较强，另外两个叶片回波能量相对较弱，所以能量较强的部分主要在零频到最大多普勒频率分布。在功率谱和时频谱中可以看出两种信号的不同特征，本文根据风轮机杂波不同于气象目标特征，采用匹配追踪算法抑制风轮机杂波并保留真实的气象目标。

在谷歌地球上获得四台风轮机的经纬度如表5所示。利用该先验信息获得每台风轮机相对于雷达的距离和方位，然后提取有效相干脉冲对应的回波数据，基于匹配追踪方法抑制风电场杂波。

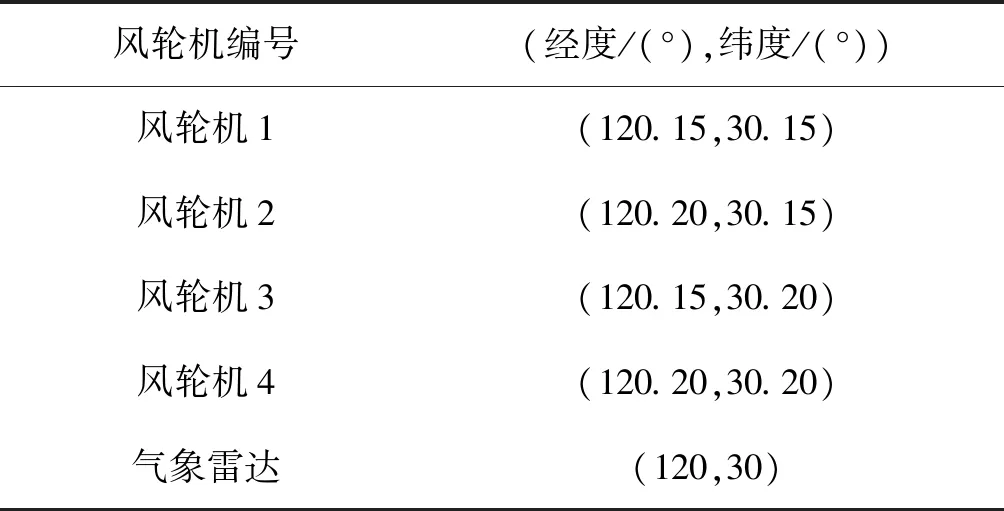
表5 四个风轮机和雷达的经纬度

采用改进的匹配追踪方法实现风电场杂波抑制的结果如图7所示，图7与图5对比分析可以看出，图5(a)中四台风轮机所在距离方位单元的回波已经剔除，同时图5(b)中四台风轮机对应的四条展宽的频谱也基本剔除。图8是第四台风轮机所在距离单元的杂波抑制后的功率谱及时频谱，与真实的气象目标结果(如图4所示)一致，由图8和图4对比可以看出，风电场杂波得到了有效的抑制。

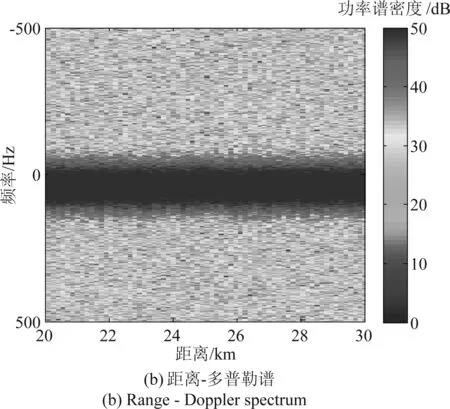
图7 风电场杂波抑制结果

图8 风轮机杂波抑制结果

5.2 性能分析

(1)算法改进前后性能分析

在参数设置、回波数据以及字典原子的数量相同的条件下，改进前后的算法运算时间对比如表6所示(该实验是在一个中央处理器为英特E5-2640的服务器上完成)。由表6数据对比可以看出，改进前抑制处理时间约三个小时，改进后五分半钟左右。可见与传统方法相比，改进算法在保证抑制性能不变的前提下，明显提高了运算效率。

表6 改进前后抑制时间对比

(2)抑制前后风轮机杂波平均功率

为了分析改进后的匹配追踪算法性能，本文在不同杂噪比(CNR)的条件下，进行了500次的蒙特卡罗实验，对比抑制前后风轮机杂波平均功率变化。抑制前后的风轮机杂波平均功率随着杂噪比(CNR)的变化性能曲线如图9所示。

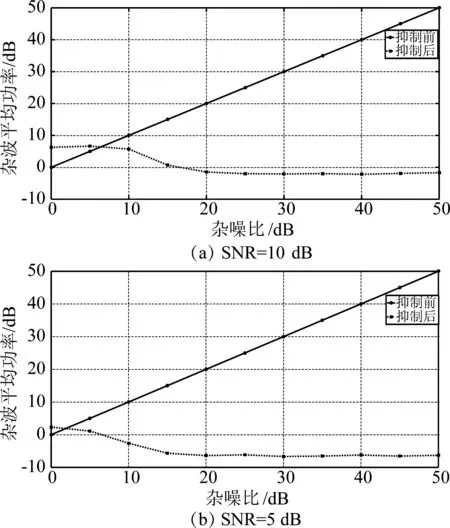
图9 抑制前后风轮机杂波平均功率随杂噪比的变化

图9(a)和图9(b)中的两条曲线分别是抑制前后风轮机杂波平均功率的变化情况，随杂噪比的增大，抑制前的杂波平均功率逐渐变大，抑制后杂波功率逐渐变小并趋于0dB以下的一个稳定值。除此之外，图9(a)和图9(b)对比可以看出，在不同信噪比的条件下该方法都能保持良好的抑制效果，信噪比的变化并不影响该方法的性能。需要说明的是，当杂噪比小于信噪比(如图9(a)中CNR小于SNR=10dB)时，抑制效果不理想，这是因为此时杂波平均功率也就等于甚至低于气象目标平均功率，依据匹配追踪算法原理找最大投影值，可能会出现匹配错误的原子，导致抑制效果不理想。也就是在信杂比(SCR)较高时，该方法抑制效果不明显。事实上，这种情况并不需要抑制杂波，因为在信杂比(SCR)较高时，也就是气象目标回波较强，此时风轮机对气象目标影响较小，无需进行杂波抑制。例如，当信噪比是10dB时，杂噪比(CNR)分别为10dB和0dB两种情况下的风轮机杂波抑制前后结果如图10所示。图10(a)和图10(c)分别是杂噪比为10dB和0dB时抑制前的雷达回波，由于杂噪比较低甚至低于信噪比，气象目标特性占主导，不能明显地看出风轮机的频谱分布。图10(b)和图10(d)是其相对应的抑制结果，杂波功率较小，抑制前后结果变化不明显。

(3)抑制前后气象目标参数估计结果

基于脉冲对法对风电场杂波抑制前后数据分别进行气象目标参数(平均功率，平均径向速以及平均谱宽)估计结果如表7所示。

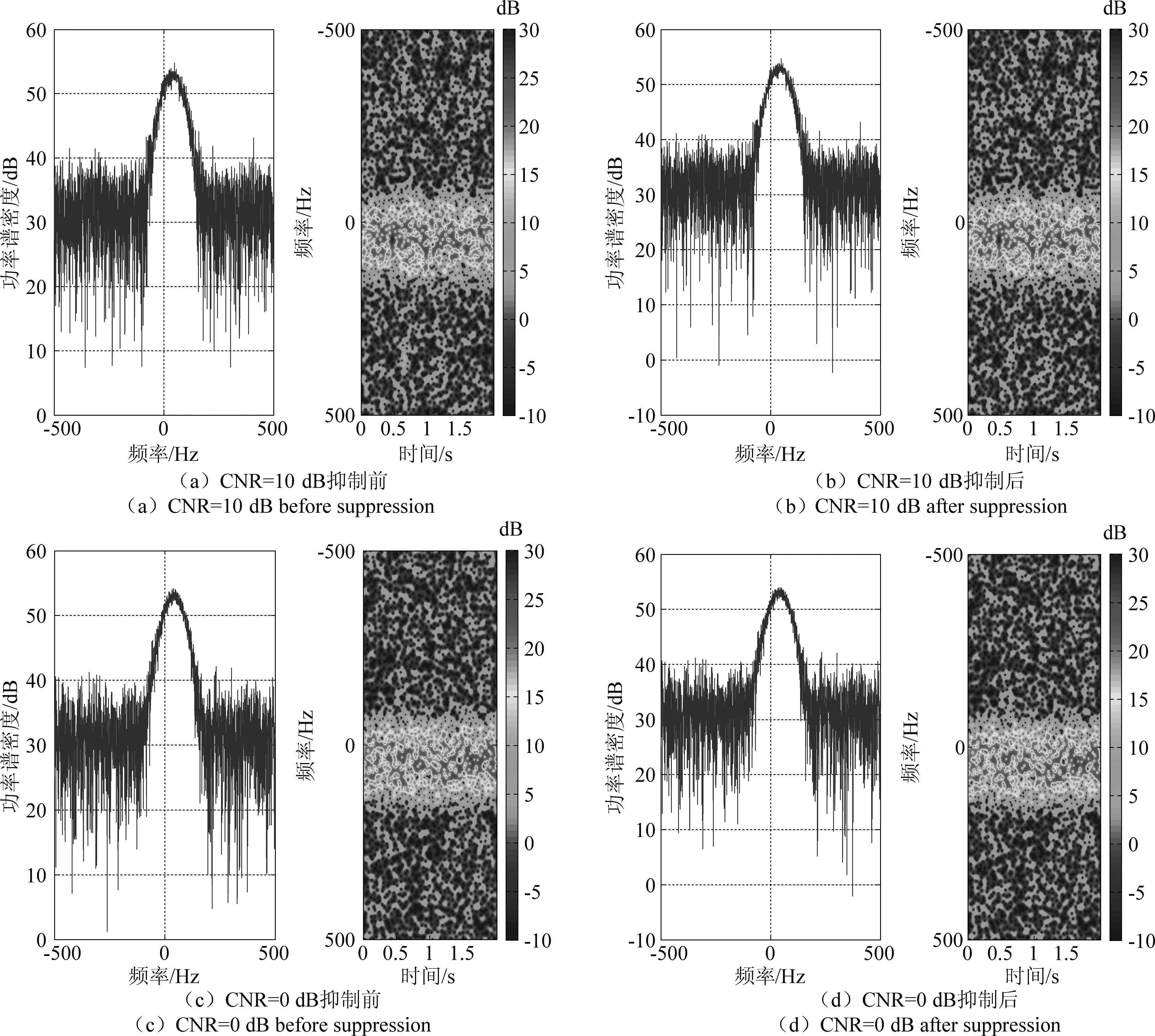
图10 抑制前后的雷达回波的功率谱和时频谱对比

目标状态平均功率/dB平均径向速度/(m/s)平均谱宽/(m/s)真实气象目标10.0002.02.0抑制前气象雷达回波29.925911.08148.6550抑制后气象雷达回波10.0011.98671.9913

由表7可以看出，抑制前的气象雷达回波参数估计值出现较大的偏差，由此可知风电场杂波对气象目标参数估计的影响较大。对气象雷达回波抑制后，参数估计值更接近于真值，杂波抑制算法效果较为显著。

6 结论

本文利用白塞尔大地主题反解算法获得雷达和风轮机的距离、方位信息，提取出雷达回波中被风电场污染的相干脉冲数据，再对该数据作杂波抑制处理。实验结果显示，改进方法在较好的保留了原有的气象目标信息的前提下抑制了大部分的风电场杂波，同时有效地降低了计算量和数据存储量，提高了运算效率。除此之外，从杂波功率去除率及气象信息保留完好性两个方面对算法的性能进行了定量的分析验证算法的有效性。本文算法中，只考虑了风轮机直达路径回波情况，没有考虑风电场中风轮机间的多径散射对抑制效果的影响，这也是后续需要进一步研究的工作。