喷丸表面粗糙度对疲劳寿命影响研究*

王 帅，王建明，吕鹤婷

(山东大学 机械工程学院CAD/CAM研究所，济南 250061)

0 引言

喷丸处理是国内外普遍认可的提高结构件抗疲劳性能的表面强化技术[1-3]，受喷工件表面及次表层中存在残余压应力，该残余压应力可部分抵消交变外载荷所产生的拉应力，并对微裂纹形成闭合效应以阻止其扩展，即喷丸残余压应力被公认为是提高工件表面抗疲劳性能的主要强化因素[4-5]。但喷丸处理不仅得到有利的表面残余压应力层，也会在工件表面留下大量致密的弹坑，使工件表面高低不平，引起表面粗糙度发生变化，在凹凸不平的工件表面谷底处容易引起应力集中和出现微裂纹[6-7]，从而对工件抗疲劳性能产生不利的影响，可被视为喷丸对工件抗疲劳性能的弱化因素，故为全面客观评价喷丸强化效果时，上述弱化因素不容忽视。前人对喷丸处理的研究大多集中在上述强化机理方面[8-10]，而对上述弱化方面的研究相对较少，且多是集中于研究喷丸对工件表面粗糙度的影响方面，而研究喷丸表面粗糙度对疲劳寿命影响的相关文献较少[11-13]。

张建荣利用ABAQUS软件根据单个弹坑的有限元结果提出表面粗糙度特征值Ra的理论预测模型[14]。章刚对平板表面形貌进行简化并建立半椭圆形微缺口有限元模型分析不同表面粗糙度下的应力场，并采用回归分析方法建立缺口间距和表面粗糙度与应力集中系数之间的经验公式[15]。Mylonas等人建立三维多丸粒喷丸强化有限元模型计算特定表面粗糙度参数，并将数值结果代入半解析方程计算应力集中系数，但并未深入探索应力集中系数与疲劳寿命之间的关系[16]。

上述针对喷丸表面粗糙度的分析均采用改变单一参数研究其影响规律的方法，未进行不同喷丸参数对表面粗糙度及形貌的影响强弱程度排序，大多未涉及表面粗糙度对疲劳寿命的影响或仅停留在定性分析阶段，未深入定量分析表面粗糙度及形貌对应力集中及疲劳寿命的影响规律。本文拟建立经实验验证的喷丸有限元模型，采用多因素正交试验法研究不同影响因素对喷丸表面粗糙度的影响程度；在此基础上，建立粗糙度与应力集中因子的相关关系，进而通过应力集中因子与疲劳裂纹萌生寿命的定量关系预测工件的疲劳寿命。

1 喷丸有限元模型建立及验证

1.1 有限元模型建立

喷丸强化属于一种高速碰撞瞬态冲击动力学接触问题。实际喷丸过程中是成千上万个弹丸反复撞击工件，而考虑到计算机性能及数值计算成本等问题，真实的模拟该物理过程是不可能的。基于ABAQUS/Explicit软件采用显式动力学算法建立如图1所示三维多丸粒喷丸强化有限元模型进行求解以最终得到稳定的应力应变响应。为节约运算成本，工件模型尺寸选择为12R×12R×10R，其中R为弹丸半径。工件底部进行完全固定，约束所有方向的自由度。弹丸选取1/2模型，对其进行刚体建模。弹丸与工件表面的接触类型为面-面接触，为限制两接触面在切向方向的相互运动在ABAQUS/Explicit中设置罚函数接触，摩擦因数设为0.2。

为提高喷丸覆盖率，本次采用搭接率为0.5的偏置法建模，使后续弹丸的冲击位置尽可能的避开前一弹丸冲击所形成的弹坑。由于工件与弹丸的接触仅发生在工件中间表面部分，仅对工件中间接触区域及其厚度方向进行局部网格细化，其它远离弹丸冲击区域网格适当放大。工件采用C3D8R三维实体缩减积分单元，弹丸采用C3D8三维实体单元。考虑到该缩减积分单元在大变形下易发生沙漏现象，故设置其沙漏刚度系数为2。

图1 多丸粒有限元模型

1.2 材料属性及本构模型

工件材料采用航空常用铝合金材料2024-T351，弹丸采用玻璃丸，两种材料的物理性能参数如表1所示。

表1 材料的物理性能参数

喷丸强化过程中，弹丸连续不断的高速冲击工件，使得工件表层材料以高应变速率发生塑性变形。Johnson-Cook本构模型综合考虑了材料应变速率及温度等因素的变化对材料力学性能的作用，故采用该本构方程来模拟工件材料变形的应力应变关系。其本构模型关系式为：

(1)

工件材料2024-T351铝合金本构模型参数的相应数值如表2所示。

表2 2024-T351铝合金的Johnson-Cook本构模型参数

1.3 模型结果验证

采用上述建模方法依照文献[10]中的实验条件建立相应有限元模型，通过实验和仿真结果的对比分析验证该仿真模型的有效性。该实验中控制喷丸强化效果的参数包括喷射气压、喷丸流量、弹丸尺寸和喷嘴至工件表面的距离等。实验研究表明，其中喷嘴距离对工件表面粗糙度的影响甚微，可忽略不计。而喷丸数值仿真模型中，通常是将弹丸直径和喷射速度作为基本仿真参数，为将仿真模型参数与实验参数相对应，利用文献[18]的公式将喷射气压和喷丸流量折合为喷丸速度：

(2)

式中，ρ—材料密度g/cm3；Q—喷丸流量，kg/min；p—喷丸气压，bar(1bar=105Pa)。

根据式(2)和文献[10]的实验参数计算得到相应的喷丸速度为v=59.29m/s。故在该验证模型中设置弹丸直径d=0.58mm，喷丸速度v=60m/s。图2是喷丸后试样YOZ截面残余应力云图，残余应力提取路线是弹丸中心与工件表面接触点沿深度方向竖直向下取大约0.6mm的采样距离，为保证提取结果的准确性，在弹丸中心与试样接触位置均布3×3条采样路径，其中一条如图2中竖线所示。实验利用X射线应力衍射仪，并结合电化学剥层的方法测量喷丸强化后铝合金试样表面残余应力场沿深度方向的分布。图3为提取的9条路径上的喷丸残余应力取平均值后的数值仿真结果与实验测量结果对比。

图2 YOZ截面残余应力云图

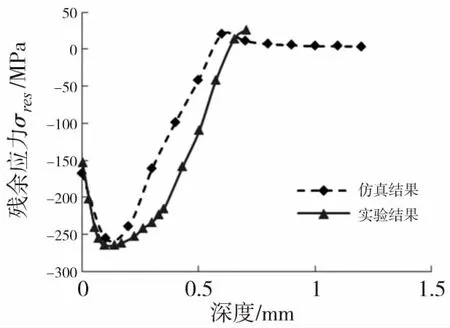
图3 喷丸残余应力分布结果对比

由图3可以看出，仿真和实验得到的残余应力变化趋势基本一致，表层为残余压应力区，该区域残余压应力首先随深度增加而不断增大，达到最大残余压应力后逐渐减小直至减为零，随后进入残余拉应力区。在工件表层至最大残余压应力区间内，两者的结果基本一致。在最大残余压应力层到残余压应力为零的区间内，两者变化趋势相同，但数值存在差异。究其原因为数值仿真模型中弹丸数目有限，而实际喷丸实验中弹丸数量众多，大量弹丸的撞击作用扩大了次表层塑性变形区域范围，因此实验曲线较仿真曲线向右侧有一定的偏移。表3给出了该喷丸残余应力曲线上的4个特征参数的实验值、仿真值及两者的误差值。由上述仿真和实验的对比分析可以看出，两者的喷丸残余应力变化趋势基本一致，且数值基本吻合，最大误差为9.42%，从而验证了该数值模型的正确性和有效性，为以下基于该模型开展仿真研究奠定了基础。

表3 喷丸残余应力仿真值与实验值对比分析

2 表面粗糙度模拟

2.1 表面粗糙度概述

喷丸强化过程中，大量弹丸连续不断的随机高速撞击工件，表层材料发生塑性变形，使工件表面形成致密的小压痕或凹坑，引起表面形貌发生变化。表面形貌可由表面粗糙度描述。本文采用表面粗糙度参数Rz表述喷丸后工件表面粗糙度的量值。

喷丸数值仿真中，通常采用喷丸工件受喷区域表面节点沿厚度方向位移的最大值和最小值之差作为表面轮廓最大高度Rz。图4所示为单弹坑位移示意图，即喷丸工件表面粗糙度Rz为：

Rz=Umax-Umin

(3)

图4 工件表面弹坑位移图

2.2 多因素正交试验

正交试验设计是目前常用的试验优化分析办法，利用标准化正交表安排实验方案，将实验中的各影响因素及其水平进行合理搭配，使之均匀分散，可使试验次数大大减少，以降低实验成本。

为寻求对表面粗糙度影响最小的喷丸工艺参数最佳组合，将表面粗糙度参数Rz作为试验指标，选择弹丸直径、弹丸数量、冲击速度和冲击角度四个影响因素设计正交试验，如表4所示。

基于上述四因素三水平L9(34)正交试验表，利用1.1节所述数值模型开展喷丸表面粗糙度正交试验研究，得到表5所示正交试验数据。

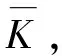
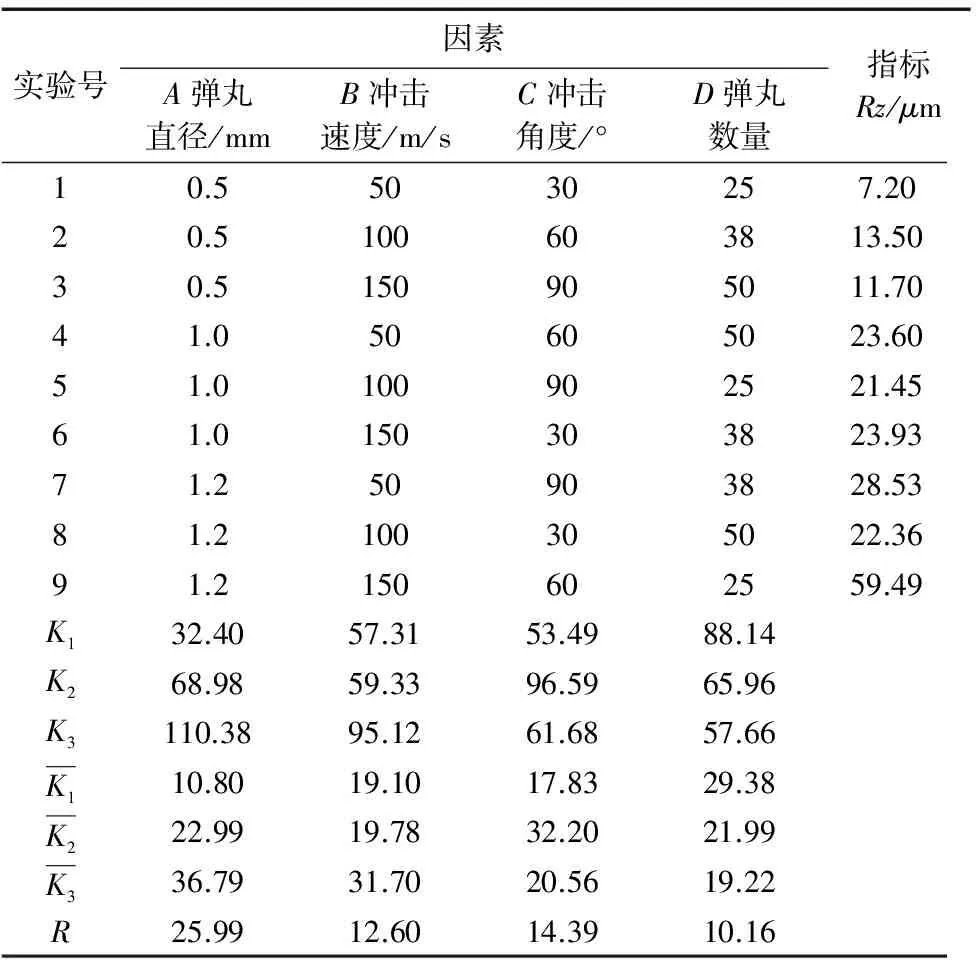
表5 正交试验表L9(34)及结果数据

图5 因素水平与指标关系图

3 裂纹萌生寿命预测

喷丸后工件表面会形成一系列凹坑，可将这些凹坑视为无数微观缺口，粗糙不平的缺口对疲劳寿命的影响可用应力集中系数Kt表示[19]，即：

(4)

式中，λ为缺口之间的距离与其深度的比值；ρ为缺口底部曲率半径。由式(4)可见，应力集中系数并非由表面粗糙度单一参数决定，还受弹坑底部曲率半径的影响，即表面粗糙度值越大，弹坑底部曲率半径越小，其表面应力集中现象越严重。针对表5对应的9种正交试验工况，计及表面粗糙度和缺口底部曲率半径，由式(4)分别得到相应的应力集中系数如表6所示。

应力集中系数将直接影响疲劳微裂纹的萌生寿命，文献[20]通过对2024-T3铝合金疲劳损伤和裂纹萌生进行大量实验研究总结出疲劳裂纹萌生寿命计算公式(5)。

(5)

n—应变硬化指数，n=0.078。

图6为表5正交试验9种方案的裂纹萌生寿命预测结果。综合分析表5、表6和图6的试验结果，方案9的表面粗糙度最大，应力集中系数最大，疲劳裂纹萌生寿命最小。表面粗糙度数值大小依次为：9>7>6>4>8>5>2>3>1，应力集中系数的大小依次为：9>2>6>7>4>3>5>8>1，疲劳裂纹萌生寿命与应力集中系数排列相反。显然，在确定加载条件下，疲劳裂纹的萌生寿命受应力集中系数Kt直接影响，Kt越大，疲劳裂纹越易萌生。而表面粗糙度仅是影响应力集中系数和疲劳寿命的因素之一，并非表面粗糙度越大，疲劳寿命越低。

表6 9种工况应力集中系数

图6 疲劳裂纹萌生寿命预测值

4 结论

本文首先将ABAQUS/Explicit建立的多丸粒喷丸强化数值模型所得到的残余应力结果与参考文献实验结果进行对比，验证了该数值模型的有效性。然后选用弹坑轮廓最大高度Rz作为表面粗糙度参数，设计了四因素三水平正交试验，研究弹丸尺寸、冲击角度、冲击速度和弹丸数量对工件表面粗糙度的影响程度，进而分析喷丸表面形貌参数与应力集中系数和疲劳裂纹萌生寿命之间的定量关系。

结果表明：①各因素对Rz的影响程度依次为：弹丸直径>冲击角度>冲击速度>弹丸数量；②在喷丸工艺设计中，应合理选择喷丸工艺参数，弹丸直径不可过大，冲击角度和冲击速度应适中，丸粒尽量达到全覆盖，以使工件表面平整，降低表面粗糙度，减小应力集中；③疲劳裂纹萌生寿命与应力集中系数呈反比关系，即Kt越大，疲劳裂纹萌生寿命越小。而喷丸表面粗糙度和弹坑底部曲率半径共同影响应力集中系数和疲劳裂纹萌生寿命，即表面粗糙度和疲劳寿命之间并非一一对应关系。

[1] Solis-Romero J, Oseguera-Pena J, Verduzco-Martinez J, et al. Surface Stress Concentration Analysis of Shot Peened Aluminium Alloys[M]. Key Engineering Materials, Balankin A, Trinidad J M, Huerta O S, 2010,449:70-76.

[2] Zhou J, Fan Y, Huang S, et al. Research and Prospect on Micro-Scale Laser Shot Peening[J]. Chinese Journal of Lasers,2011,38(6):601003-601011.

[3] 栾伟玲,涂善东. 喷丸表面改性技术的研究进展[J].中国机械工程,2005,16(15):1405-1409.

[4] Sheng X, Xia Q, Cheng X, et al. Residual stress field induced by shot peening based on random-shots for 7075 aluminum alloy[J]. TRANSACTIONS OF NONFERROUS METALS SOCIETY OF CHINA,2012,222, S261-S267.

[5] 高玉魁. 喷丸对Ti-10V-2Fe-3Al钛合金拉-拉疲劳性能的影响[J].中国有色金属学报,2004,14(1): 60-63.

[6] Laue S, Bomas H, Hoffmann F. Influence of surface condition on the fatigue behavior of specimens made of a SAE 5115 case-hardened steel[J]. Fatigue & Fracture of Engineering Materials & Structures, 2006, 29(3): 229-241.

[7] Solis-Romero J, Oseguera-Pena J, Verduzco-Martinez J, et al. Surface Stress Concentration Analysis of Shot Peened Aluminium Alloys[M]. Key Engineering Materials, Balankin A, Trinidad J M, Huerta O S, 2010,449:70-76.

[8] 王欣, 蔡建明, 王强,等. 喷丸表面覆盖率对Ti60高温钛合金疲劳性能的影响[J]. 中国表面工程, 2011, 24(5): 58-63.

[9] Bhuiyan M S, Mutoh Y, McEvily A J. The influence of mechanical surface treatments on fatigue behavior of extruded AZ61 magnesium alloy[J]. Materials Science and Engineering: A, 2012, 549: 69-75.

[10] 王明涛, 曾元松, 黄遐. 大尺寸弹丸喷丸成形2024-T351铝合金表面质量研究[J]. 航空制造技术, 2012(5): 92-94.

[11] Dai K, Villegas J, Stone Z, et al. Finite element modeling of the surface roughness of 5052 Al alloy subjected to a surface severe plastic deformation process[J]. Acta Materialia, 2004, 52(20): 5771-5782.

[12] Klemenz M, Hochrainer T, Delonnoy L, et al. Similarity rules for the shot peening process based on finite element simulations[C]. International Conference of Shot Peening ICSP-9, Paris.,2005, 94-99.

[13] Miao H Y, Larose S, Perron C, et al. On the potential applications of a 3D random finite element model for the simulation of shot peening[J]. Advances in Engineering Software, 2009, 40(10): 1023-1038.

[14] 张建荣, 程秀全, 盛湘飞,等. 喷丸工艺对7075铝合金表面粗糙度的影响[J]. 轻合金加工技术, 2014, 42(9): 54-59.

[15] 章刚, 刘军, 刘永寿, 等. 表面粗糙度对表面应力集中系数和疲劳寿命影响分析[J]. 机械强度, 2010, 32(1): 110-115.

[16] Mylonas G I, Labeas G. Numerical modelling of shot peening process and corresponding products: Residual stress, surface roughness and cold work prediction[J]. Surface & Coatings Technology, 2011,205(19): 4480-4494.

[17] Meguid S A, Shagal G , Stranart J C, et al. Three-dimension dynamic finite element analysis of shot peening induced residual stress[J]. Finite Elements in Analysis and Design, 1999, 31: 1792-191.

[18] Klemenz M, Schulze V, Vöhringer O, et al. Finite Element Simulation of the Residual Stress States after Shot Peening[J]. Materials Science Forum, 2006, 524-525: 349-354.

[19] Arola D, Williams C L. Estimating the fatigue stress concentration factor of machined surfaces[J]. INTERNATIONAL JOURNAL OF FATIGUE,2002,24(9):923-930.

[20] Zheng X. A further study on fatigue crack initiation life-mechanical model for fatigue crack initiation[J]. International Journal of Fatigue, 1986, 8(1): 17-21.