云制造环境下资源受限的同类机调度问题
2018-03-07,,
,,
(浙江理工大学理学院,杭州 310018)
0 引 言
云制造(Cloud manufacturing)是一种新型制造模式,能够把分散的资源整合在一起,然后经过虚拟化实时发布资源的利用状态,实现资源共享,提高资源的利用率。因此云制造对于我国的经济发展有着深远的意义。本文主要研究了在云制造背景下资源受限的同类平行机调度问题。机器的所有者通过云制造平台把机器的现有状态包括租用成本、加工速度、机器的使用情况进行虚拟化发布。生产方通过云制造平台获知机器的现有状态,根据自己的成本预算选择最适合自己的机器,并安排工件加工。
本文考虑以下问题:每台机器都有一个加工速度和租用的固定成本,其中固定成本不随加工时间变化而变化,生产方的成本预算(资源)是一个固定常数;目标是在给定的成本预算情形下,租用相应的机器并加工工件使得最大完工时间(Makespan)最小。

本文考虑文献[13]所提问题的两种更一般的情况。第一种情况假设工件的长度不完全相同,机器速度越大,其单位成本速度也越大;第二种情况中工件的长度相同但对机器没有要求。本文分别对上述两种情形给出了近似算法及其最坏情况界。
1 符号定义
本文引入以下符号。
m:云制造平台提供的的机器数;
n:云制造平台得到的需要加工的工件数,n≥m;
M={Mi|i=1,2,…,m}:云制造平台提供的机器集合;
J={Jj|j=1,2,…,n}:云制造得到的需要加工的工件集合;
pj:工件Jj的长度;
si:机器Mi的加工速度,即单位时间加工的工件长度;
Ki:机器Mi的加工成本;

U:机器加工工件需要的总成本;
Li:机器Mi的负载;
Cmax(A):算法A的目标函数值(makespan);
Cmax(opt):最优调度的makespan。
2 工件长度不同的同类机调度问题


算法A1:
1) 令U=0,h=0,M′=∅,i=1.
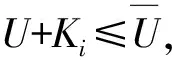
3)i++,若i≤m,返回第2步;否则进行到下一步。

5) 令a=M′,选择的机器集合M′={M1,M2,…,Mh-1}∪{Mj1,Mj2,…,Mjk},其中k+h-1=a且jk>jk-1>…j1>h。
6) 把工件按照其加工时间从大到小进行排序即p1≥p2≥…≥pn。
7) 令j=1;ti=0,Li=∅.

9) 若j≤n,则返回第上一步;否则,停止。


证明:(ⅰ) 令Γ表示前h台机器的集合,即Γ={M1,M2,…,Mh}。设M*表示最优排序中机器的集合,根据假设可以得到


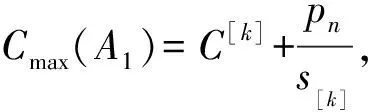
化简可得
Cmax(A1)s[i]≤C[i]s[i]+pn。
由此可得

因此
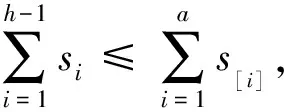

证明:由引理1可知
化简可得
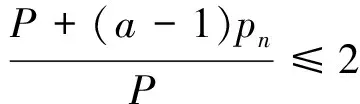
3 工件长度相同的同类机调度问题

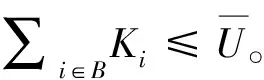
算法A2:
2) 令U=0,h=0,B=∅,i=1。

4)i=i+1,若i≤m,则返回第3步;否则进行到下一步。
6) 令b=B,选择的机器B={M1,M2,…,Mh-1}∪{Mj1,Mj2,…,Mjk},其中k+h-1=b且jk′>jk-1′>…>j1′>h。
7) 令j=1;ti=0,Li=∅。

9) 若j≤n,则返回第上一步;否则,停止。

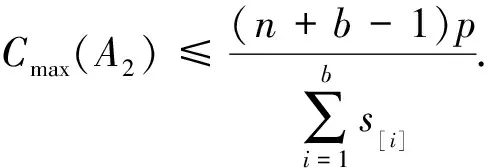
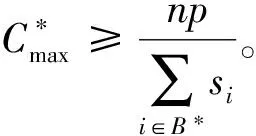
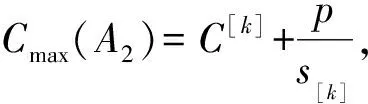
化简可得
Cmax(A2)s[i]≤C[i]s[i]+p。
由此可得

≤(n+b-1)p。
即
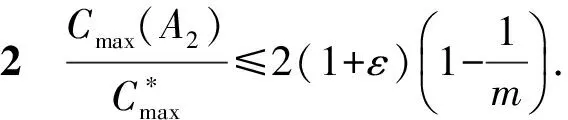
证明:由引理2可知
算法A2选择的机器数为b,且b≤m-1。结合n≥m可得

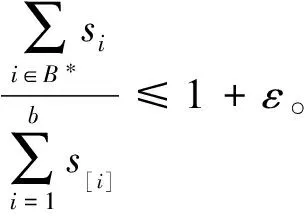
4 结 论
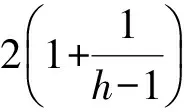
[1] 李伯虎,张霖,王时龙,等.云制造:面向服务的网络化制造新模式[J].计算机集成制造系统,2010,16(1):1-7.
[2] 李伯虎,张霖,任磊,等.再论云制造[J].计算机集成制造系统,2011,17(3):449-457.
[3] 李伯虎,张霖,任磊,等.云制造典型特征、关键技术与应用[J].计算机集成制造系统,2012,18(7):1345-1356.
[4] Noga J. Scheduling with machine cost[C]//International Workshop on Approximation Algorithms for Combinatorial Optimization Problems: Randomization, Approximation, and Combinatorial Algorithms and Techniques. Springer-Verlag,1999:168-176.
[5] Imreh C. Online scheduling with general machine cost functions[J]. Electronic Notes in Discrete Mathematics,2006,27(9):49-50.
[6] Jiang Y W, He Y. Preemptive online algorithms for scheduling with machine cost[J]. Acta Informatica,2005,41(6):315-340.
[7] Dosa G, Tan Z Y. New upper and lower bounds for on line scheduling with machine cost[J]. Discrete Optimization,2010,7(3):125-135.
[8] Rustogi K, Strusevich A V. Parallel machine scheduling: Impact of adding extra machines[J]. Operations Research,61(5):1243-1257.
[9] Jiang Y W, He Y. Semi-Online Algorithms for scheduling with machine cost[J]. Journal of Computer Science and Technology,2006,21(6):984-988.
[10] He C, Leung YT, Lee K, et al. Scheduling a single machine with parallel batching to minimize makespan and total rejection cost[J]. Discrete Applied Mathematics,2016,204(C):150-163.
[11] Lee K, Leung YT, Jia Z H, et al. Fast approximation algorithms for bi-criteria scheduling with machine assignment costs[J]. European Journal of Operational Research,2014,238(1):54-64.
[12] Li K, Zhang X, Leung YT, et al. Parallel machine scheduling problems in green manufacturing industry[J]. Journal of Manufacturing Systems,2016,38:98-106.
[13] Li K, Zhang H J, Cheng B Y, et al. Uniform parallel machine scheduling problems with fixed machine cost[J/OL]. Optimization Letters,2016[2017-09-08]. https://doi.org/10.1007/s11590-016-1096-3.
[14] Horowitz E, Sahni S, Sahni, S. Computing partitions with applications to the knapsack problem[J]. Journal of the Acm,1974,21(2):277-292.
