高滩陡坡地形下电力设施海堤的越浪量试验
2018-03-06金超杰张芝永王永举周建炯
金超杰,邵 杰,张芝永,王永举,周建炯
(1.国网浙江省电力公司杭州供电公司,浙江 杭州 310002;2.浙江省河口海岸重点实验室,浙江 杭州 310020; 3.浙江省水利河口研究院,浙江 杭州 310020)
随着沿海资源开发利用的持续增长,海岛地区的经济得以迅速发展,用电量不断增大,而海岛地区土地资源匮乏,不少电力设施只能临海而建。受自然条件及地理位置的制约,电力设施海堤常常直面开敞海域且海堤纵深非常有限,易遭遇强潮大浪的正面冲击,一旦大量水体越浪,后果不堪设想。为保证海岛地区电力设施等的安全,如何科学有效地降低海堤越浪量正受到了电力、水利、海洋、环保等多行业领域的空前重视。
多年来,海堤越浪问题一直是海岸工程领域最受关注的热点问题之一,国内外学者从20世纪初开始便开展研究,目前已取得了许多成果。国外Saville等[1-7]对海堤越浪量进行了专门的研究;国内的研究始于20世纪60年代,90年代章家昌等[8-9]通过模型试验提出了海堤平均越浪量计算公式,并被JTJ 213—98《海港水文规范》引用并延续至JTS 145—2015《港口与航道水文规范》;21世纪初陈国平等[10-12]也通过系统深入的研究提出了越浪量计算公式;2014年常江等[13]系统研究了斜坡堤堤顶宽度对越浪量的影响规律。然而规范公式及各家研究成果并不适用于海岛地区电力设施海堤所在高滩陡坡环境,外海大浪传至近岸后,因海堤前沿海床地形较陡,水深变浅后的破碎波高仍然很大,若盲目加高此类海堤的堤顶高程,势必对电力设施的地基承载条件带来一定的负面影响。本文以浙江舟山某海岛临海而建的电力工程为例,通过模型试验研究电力设施海堤在高滩陡坡地形下的越浪量变化规律,并据此提出合理的迎浪面结构设置方式。
1 物理模型设计
试验在波浪水槽(长70 m、宽1.2 m、高1.7 m)内进行,首端采用液压式推板造波机造波,末端设有消能缓坡以减少波浪反射。水槽纵向分为两部分,外侧0.5 m宽度内用于试验断面,内侧则用于消除波浪的二次反射。物理模型按正态重力相似准则设计,根据波要素、试验断面及设备性能等因素,确定模型比尺λ=20。
试验模拟对象的电力设施海堤处于高滩环境,堤前水深d=2.86 m,入射波的波周期T=15.1 s;入射波传至高滩陡坡地形时波列中波高H13%以上的大波均都已破碎,模型试验时只能采用规则波进行模拟。规则波的平均波高按波列的破碎波高值控制,破波参数查规范后取0.85,则堤脚处的破碎波高为2.43 m(以下统称波高H)。
在波浪传播方向沿程设置4根波高仪,以确保波态平稳、4个测点的波要素率定结果均满足JTJ/T 234—2001《波浪模型试验规程》的相关误差要求。
在浙江沿海,海岛电力设施海堤的上部防浪墙常采用直墙形式,其外侧往往采用带平台的复式结构以达到消减波浪、稳定堤基的作用。如何合理设置平台与陡墙的相对位置,灵活控制好消浪平台的宽度及高程,在不占用太多土地面积的同时尽可能地消减外海来波,是本文物理模型的设计原则。鉴于此,海堤护脚坡度m=3不变,采用不同的防浪墙高度P(防浪墙顶高出平台的高度),并组合不同的消浪平台超高Δh(平台高出静水面的高度)及平台宽度B作为海堤越浪量的影响因子,试验组次如下:①相对平台超高Δh/H=0.25、0.50、0.60、0.75、1.00;②相对平台宽度B/H=2、4、6、8;③防浪墙高度P=0.9 m、1.2 m、1.5 m。将上述变量进行组合,共开展5×4×3=60组越浪量试验,越浪量采用集水称重法量测,每组越浪量试验重复3次取其平均值以减小偶然因素的影响。

图1 试验断面及各物理参数示意图
2 海堤越浪量的影响因子分析
当波浪与海堤相遇后,波形在护脚斜坡的上方发生较大变形,波峰的推进速度加快、波谷减缓,使得波面的前坡变陡、后坡变坦。在遇到消浪平台时因局部水深减小,使得波峰面失去平衡而倾倒,波浪发生破碎,破碎的波流水体经平台沿防浪墙上爬,一部分水体漫过堤顶形成越浪,一部分水体被防浪墙挡回海侧,与下一个入射来波相遇,继续冲击海堤迎浪面(图2)。

图2 Δh/H=0.75、B/H=4、P=1.5 m组次的试验现象
2.1 平台宽度的影响
对于开敞海区,长波涌浪出现的频率较高,其波长往往有几十米甚至百米以上,海堤迎浪面的平台宽度一旦不够,长波携带的大量水体容易直接穿越平台,涌向防浪墙后形成整体越浪现象。平台宽度B作为影响越浪量q的一个主要因素,在此引入相对平台宽度B/H这一无因次量,图3为各组次下q随B/H的变化情况。由图3可见,在相同平台超高、相同防浪墙高度的前提下,各组次下q均随B/H的增大而减小,尤其是相对平台超高h/H越小的组次,平台宽度对越浪量的影响越发明显。

图3 各组次下q随B/H的变化
对于大越浪量组次,如q>0.05 m3/(m·s)时,随着平台宽度的增大,越浪量的减小趋势在较小越浪量组次更为明显;尤其是平台宽度B自6H增大至8H过程中,越浪量有较大幅度的减小,这是由于此时平台宽度的增大加剧了波浪的破碎程度,水体紊动损耗的动能显著增大,随着波流水体爬行距离的变长,越浪量得以显著减小。
对于越浪量不大的试验组次,如q<0.02 m3/(m·s)时,平台宽度B自2H增大至4H过程中,越浪量有一定幅度的减小,而当B自4H进一步增大至6H甚至8H时,越浪量的减小则迅速趋于平缓。这是由于此时受平台影响而破碎损耗的水体紊动能量趋于饱和,越浪量的小幅减小仅仅是水体在消浪平台上爬行距离增大导致的。
2.2 平台超高的影响
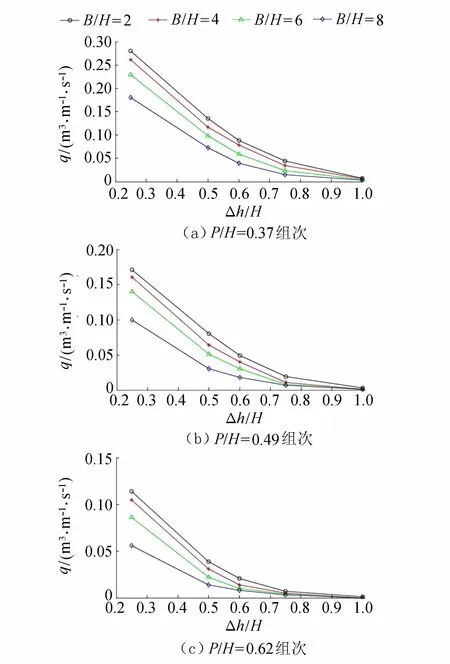
图4 各组次下q随Δh/H的变化
迎浪面的消浪平台是海堤防潮防浪的主要部位,平台高程的设置对越浪量有较明显的影响。根据以往关于复式海堤的越浪量试验成果,波浪的强作用区位于静水位上、下半倍波高范围内,设置消浪平台后将直接加剧波浪的破碎,波流水体因紊动损耗大量能量,从而直接减小了海堤堤顶的越浪量。在此引入相对防浪墙高度Δh/H这一无因次量,图4为各组次下q随Δh/H的变化情况。由图4可见,在相同平台宽度、相同防浪墙高度的前提下,随着消浪平台的增高,越浪量随之减小。当Δh自0.25H增大至0.5H过程中,越浪量的减小速率较快;而当Δh自0.6H增大至0.75H甚至1H时,越浪量的减小则趋于平缓。
2.3 防浪墙高度的影响
防浪墙作为海堤防潮防浪的主要结构部位,它将改变波流水体传至海堤上部结构处的运动状况,平台高程上防浪墙高度P的增大势必会有效消减一部分波浪能量,从而直接减小越浪量。防浪墙高度作为影响越浪量的一个主要因素,在此引入相对防浪墙高度P/H这一无因次量,图5为各组次下q随P/H的变化情况。由图5可见,在相同平台超高、相同平台宽度的前提下,各组次q均随着P/H的增大而减小,尤其是相对平台超高Δh/H越小的组次,防浪墙高度P对越浪量的影响越发明显。

图5 各组次下q随P/H的变化
2.4 影响因子的敏感性分析
依据上述试验结果,进一步分析平台宽度B、平台超高Δh、防浪墙高度P三大影响因子对电力设施海堤越浪量影响程度的敏感性,考虑到这3个因子不存在交互关系,可借助正交试验分析软件, 作三因素三水平的方差分析。选择P/H、Δh/H、B/H为三因素,三水平的取值为P/H=0.37、0.49、0.62,Δh/H=0.25、0.5、0.75,B/H=2、4、6。
方差分析的结果表明,P/H、Δh/H、B/H的偏差平方和分别为0.015、0.040和0.005,相应的F检验统计量值分别为0.750、2.000、0.250。由此可见,影响越浪量三大因素的主次顺序分别为Δh/H、P/H、B/H,即平台超高对越浪量的影响最为显著,防浪墙高度次之,平台宽度影响最小。
3 防浪结构形式
3.1 越浪量与防浪墙顶超高的关系
由于Δh/H及P/H对电力设施海堤的越浪量影响最大,将两因子相加,得到相对防浪墙顶超高Hc/H=Δh/H+P/H,其中防浪墙顶超高Hc指防浪墙顶高出静水面(设计高潮位)的高度。图6为q随Hc/H的变化情况。由图6可见,随着Hc/H的增大,q呈现明显的减小趋势,且趋势总体上逐渐变缓,各平台宽度组次下的规律性较为一致。

图6 各组次下q随Hc/H的变化

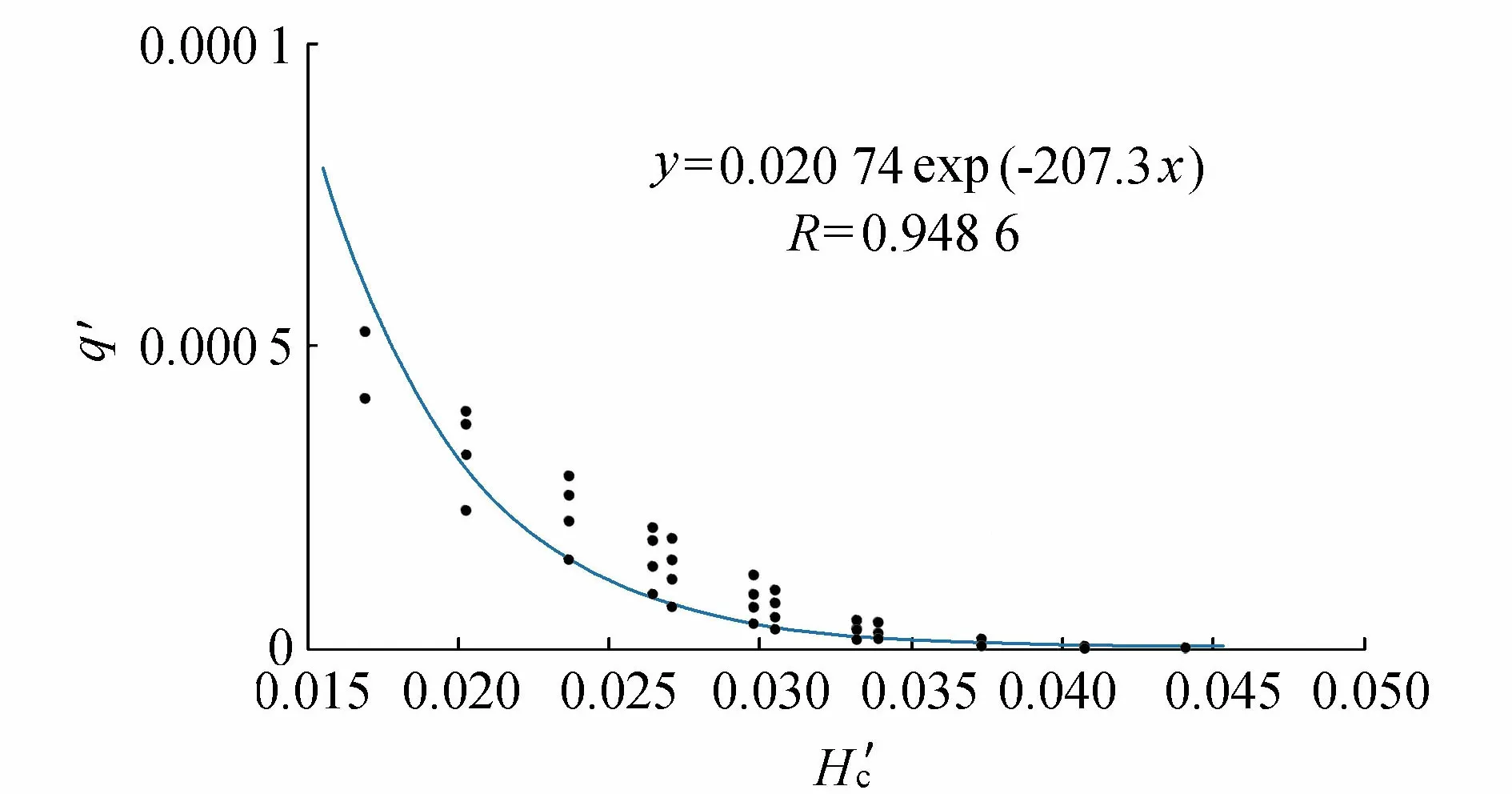
图7 各组次下q′随的变化
3.2 防浪结构的合理设置
考虑到地基条件、工程造价等因素,电力设施海堤的防浪墙顶高程不宜过高,但图6试验结果表明防浪墙顶高程至少高于设计高潮位1.2H~1.4H以上才能最大限度地限制电力设施海堤的越浪量。从单因子考虑,消浪平台的高程应高于设计高潮位,在平台超高不大于0.5H时能较好地发挥平台的消浪效果。防浪墙顶高程及消浪平台高程确定后,防浪墙高度也随之确定。在此基础上设置平台宽度,推荐平台宽度尽量不小于6H,以确保在长周期波条件下平台仍具备一定的消浪效果。在各影响因子敏感性分析基础上结合越浪量的变化规律,可以对海堤迎浪面各部位进行合理设置,从而确保电力设施海堤的防浪安全与工程经济性。
4 结 论
a. 平台超高对越浪量的影响最为显著,防浪墙高度次之,平台宽度影响最小。

c. 按防浪墙顶高程、平台高程、平台宽度的先后顺序,提出了电力设施海堤迎浪面结构的合理设置方式。
d. 考虑到波浪与海堤相互作用的影响因子众多、随机性大,加之作用过程中的波能耗散原理至今未被完全掌握,下一步可以考虑重点研究电力设施海堤越浪量与波浪要素、波浪形态的关系,以期在作用机制上有所突破,并可结合数学模型进行比较。
[1] SAVILLE T.Laboratory data on wave runup and overtopping[M] Washington,D.C.:U.S.Army,Crops of Engineers,Beach Erosion Board,1955.
[2] SAVILLE T.Large-scale model tests of wave run up and overtopping on shore Structures[M].Washington,D.C:U.S.Army,Corps of Engineers,Beach Erosion Board,1958.
[3] YUICHI I,AKIRA S,MASAO I.Effect of wave height and sea water level on wave overtopping and wave run-up[J].Coastal Engineering in Japan,1965,8:141-151.
[4] WEGGLE J R.Wave overtopping equation[C]//Proceedings of 15th Conference on Coastal Engineering.Honolulu:ASCE,1976.
[5] OWEN M W.Design of seawalls allowing for overtopping[R].Wallingford:HR Wallingford,1980.
[6] OWEN M W.Overtopping of sea defences[C]//Proceeding of International.Conference on Hydraulic Modelling of Civil Engineering.Coventry:BHRA Structures,1982.
[7 ]OWEN M W.Effectiveness of recurved wave return wall[R].Wallingford:HR Wallingford,1991.
[8] 章家昌,周家宝,王红.越浪量模型试验研究报告[R].南京:南京水利科学研究院,1992.
[9] 王红,周家宝,章家昌.越浪量模型试验研究报告(补充内容的条文和说明)[R].南京:南京水利科学研究院,1995.
[10] 陈国平.波浪爬高及越浪量研究[R].南京:河海大学,2008.
[11] 陈国平,周益人,琚烈红.海堤护面型式对波浪爬高和越浪的影响[J].水运工程,2005(10):28-30.(CHEN Guoping,ZHOU Yiren,JU Liehong.Influence of protective styles of seawall on wave runup and overtopping[J].Port & Waterway Engineering,2005(10): 28-30.(in Chinese))
[12] 陈国平,周益人,严士常.不规则波作用下海堤越浪量试验研究[J].水运工程,2010(3):1-6.(CHEN Guoping,ZHOU Yiren,YAN Shichang.Test study on wave overtopping under irregular wave action[J].Port & Waterway Engineering,2010(3): 1-6.(in Chinese))
[13] 常江,柳淑学,李金宣.斜坡堤堤顶宽度对越浪量影响的试验研究[J].水动力学研究与进展:A辑,2014(5):544-551.(CHANG Jiang,LIU Shuxue,LI Jingxuan.Experimental research on influence of the crest width on overtopping discharge over sloping breakwater[J].Chinese Journal of Hydrodynamics(Part A),2014(5): 544-551.(in Chinese))
