中长周期波作用下防浪墙前波浪力分析
2020-06-01林朝霞姜宁林王君辉
林朝霞,姜宁林,王君辉
(1.中国港湾工程有限责任公司,北京 100027;2.中交第二航务工程勘察设计院有限公司,湖北 武汉 430060)
1 研究背景
近些年来,随着港口工程的不断发展,工程所面临的外海自然条件也越来越复杂,尤其是面对周期长、波高大的恶劣建港条件时,防浪墙前波浪的作用情况也相对较为复杂,而防浪墙的稳定设计直接影响其后方掩护范围内人员及设备的安全。因此,结合工程实例探讨中长周期波浪作用下防浪墙前波浪力作用特征对于保证工程设施安全运营、港口工作人员的安全作业以及工程建成后的经济效益均具有重要的实际意义。
在水运工程领域,一般认为周期小于10 s 为短周期波,当周期大于10 s 小于30 s 时界定为中长周期波,而周期大于30 s 则为长周期波。我国沿海港口码头工程面临的一般为短周期波环境。但在越来越多的海外工程项目中,面临中长周期波环境的挑战。在引堤、防波堤等工程中,如何进行中长周期波作用下防浪墙前波浪力的计算不仅关系到结构的安全,同时也关系到工程总投资的控制。对于防浪墙前波浪力的计算,中英规范所推荐的计算公式均为根据典型条件下物模试验结果得到的经验公式,但在具体的公式组成上有较为明显的区别[1-5]。本文在依据规范进行分析计算的基础上,进一步根据物模试验实测结果对规范计算结果进行复核,最后给出中长周期波作用下引堤防浪墙稳定设计的建议。本文分析成果可为海外项目工程技术人员及国内规范修订提供一定的参考。
2 国标防浪墙前波浪力计算
JTS 145—2015《港口与航道水文规范》对于单位长度防浪墙上的总波浪力计算规定如下[2]:

式中(仅列出主要参数,其余详见规范相关条文):P 为单位长度防浪墙上的总波浪力,kN/m;为平均压力强度,kPa;d1为防浪墙前水深,m;Z 为防浪墙波浪压强分布图的顶部距静水面的高度,m;γ 为水的重度,kN/m3;H 为建筑物所在处行进波波高,m,采用H1%;Kp为与无因次参数ξ 及波坦L/H 有关的平均压强系数;KZ为与无因次参数ξ 及波坦L/H 有关的波压力作用高度系数;d为建筑物前水深,m;L 为波长,m。
防浪墙底面上的波浪浮托力计算规定如下:

式中:Pu为单位长度防浪墙底面上的波浪浮托力,kN/m;μ 为波浪浮托力的折减系数,取为0.7;B为防浪墙底宽,m。
需要说明的是:上述计算公式是针对墙前无掩护情况。 JTS 154—2018《防波堤与护岸设计规范》已有墙前全掩护条件下波浪折减规定。本项目墙前为部分掩护情况,基于保守考虑,计算中波浪力未考虑折减。建议在后续规范修订中补充墙前部分掩护情况下波浪力折减系数的说明。
3 英标防浪墙前波浪力计算
英标中推荐采用彼得森公式进行防浪墙前波浪力计算。彼得森公式为针对不规则波浪基于小尺度的物模试验得到计算公式,其具体计算规定如下[3-4]:

式中:Pi为单位长度防浪墙底面上的波浪压强,kN/m;Ru,0.1%为 0.1%波浪对应的爬高,m;Rca为静水面到引堤肩台的高度,m; y 为波浪作用楔形厚度,m;α 为引堤斜坡面的角度,(°);yeff为有效波压力作用高度,m; dca为引堤肩台顶距防浪墙顶的高度,m;Lom为与平均波周期对应的深水波长,m;Ba为防浪墙前肩台的宽度,m;dc,prot为防浪墙的埋入深度,取值如图1(a);FH,0.1%为防浪墙前波浪力,kN。
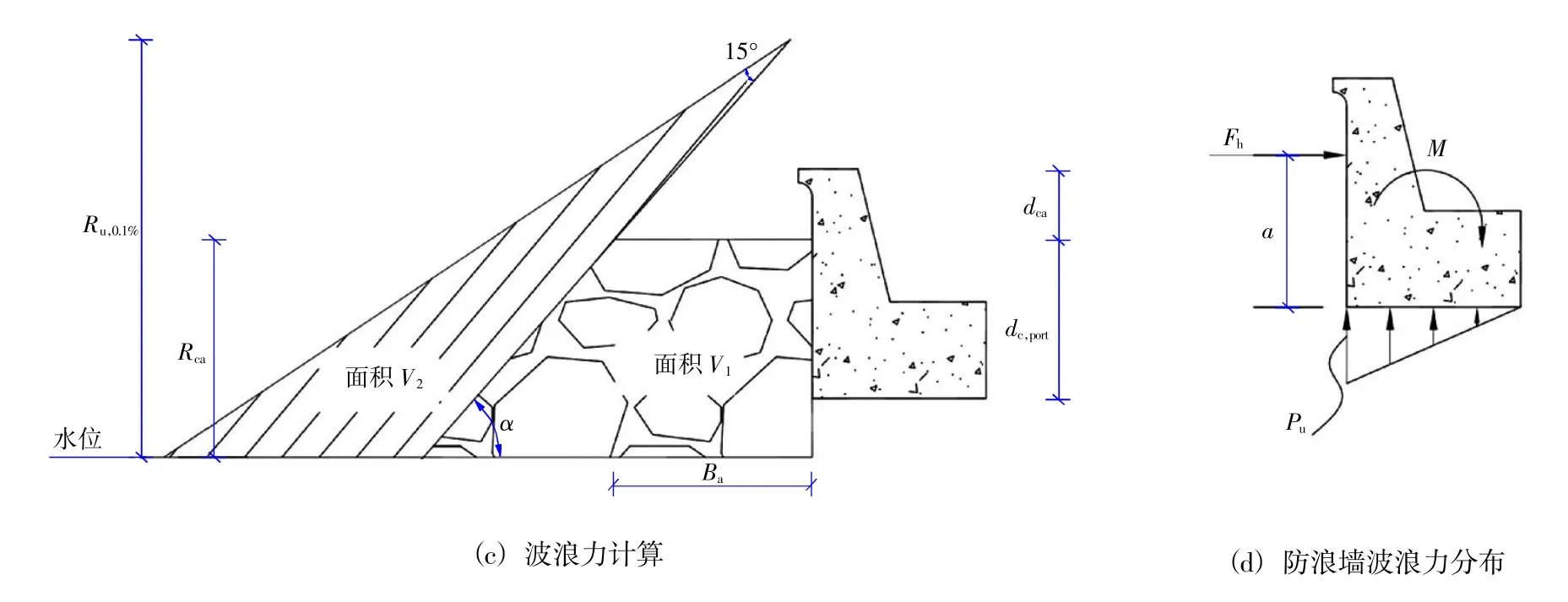
图1 彼得森公式波浪力计算示意图Fig.1 Wave force calculation diagram by Petersen formula
由波浪力产生的沿防浪墙后趾的弯矩及波浪浮托力计算规定如下:
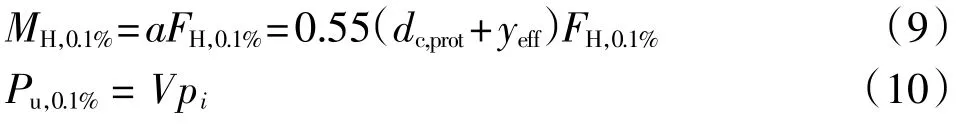
式中:MH,0.1%为波浪力产生的沿防浪墙后趾的弯矩,kN·m;a 为波浪力作用力臂,m;Pu,0.1%为波浪浮托力,kN。见图1(b)。
波浪爬高采用Van der Meer 和Stam 公式进行计算,具体规定如下:


式中:s0为波陡;H 为波高,m;Hmo表示有效波高,m;Ru,n%为对应于n%波浪的爬高,m;A、B、C、D 为常数,对于0.1%波浪,A=1.12,B=1.34,C=0.55,D=2.58;ξm为波浪破碎参数。
4 工程实例
某海外工程煤炭进口码头项目,码头平面布置采用离岸式的布置形式,码头与陆域通过引桥及引堤进行连接,其中引堤上设防浪墙的典型结构断面图如图2 所示。

图2 引堤上设防浪墙的典型结构断面图Fig.2 Cross section of typical causeway structure with wave wall
防浪墙采用顶部圆弧式结构,防浪墙顶标高12.5 m、底标高5.49 m、总高度7.01 m,防浪墙底板宽为4 m。防浪墙设计波浪参数如表1 所示,从表1 可知,不同重现期下波浪的平均波周期均超过10 s,属于典型的中长周期波。
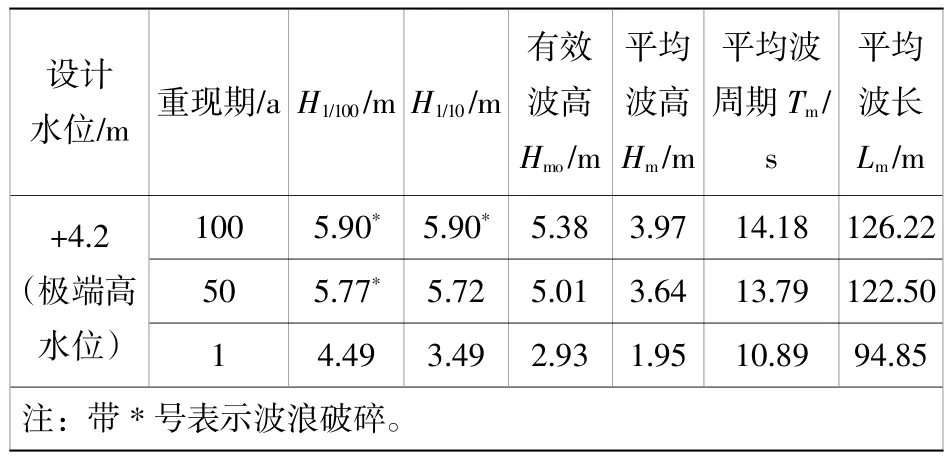
表1 防浪墙设计波浪参数Table 1 Design wave parameters of wave wall
4.1 国标防浪墙前波浪力计算结果
根据《港口与航道水文规范》[2]进行计算,防浪墙前波浪力计算结果如图3 所示。

图3 国标防浪墙前波浪力分布图Fig.3 Wave force distribution in front of wave wall by Chinese code
4.2 英标防浪墙前波浪力计算结果
根据英标推荐的彼得森公式进行计算[3-4],防浪墙前波浪力计算结果如图4 所示。
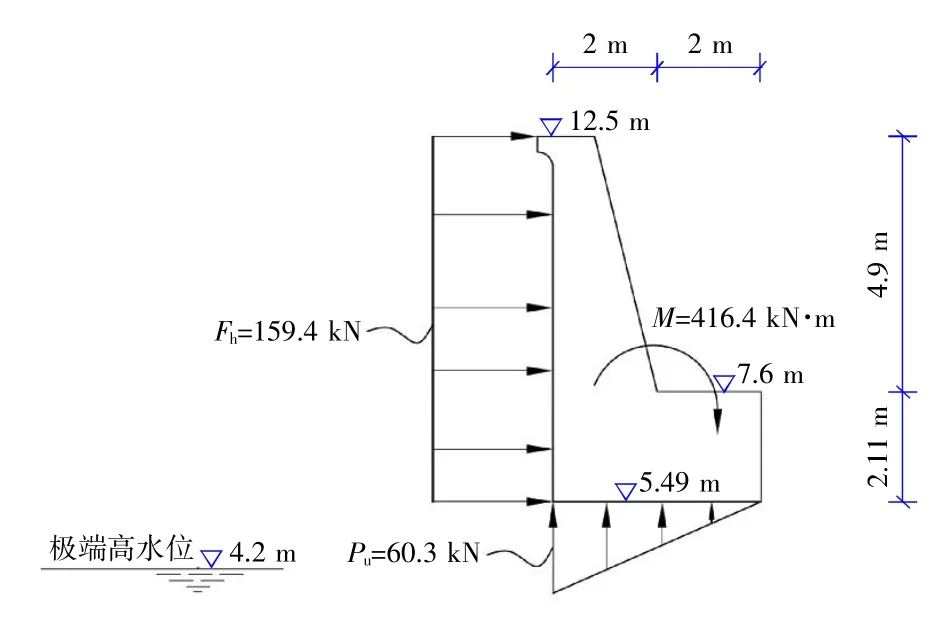
图4 英标防浪墙前波浪力分布图Fig.4 Wave force distribution in front of wave wall by BS code
需要特别说明的是,根据彼得森公式,本工程0.1%波浪对应的爬高为Ru,0.1%=13.88 m,按照该波浪爬高计算所得波浪水平力为231.2 kN。考虑到防浪墙顶高程仅为12.5 m,超出该高程的部分无受力实体结构,在实际设计中认为当波浪爬高超过防浪墙顶高程时,取防浪墙顶高程作为波浪力作用的最高点。
4.3 物模试验实测防浪墙前波浪力
物模试验中通过在防浪墙墙身迎浪面安装压力传感器测量防浪墙上波浪压强,物模试验中采用的是不规则波,波浪力结果为多组次实验的平均值,波高采用的是H1%。防浪墙上实测波浪力分布如图5 所示,从图中可以看出,有护面块体掩护位置处的波浪力明显小于无护面块体掩护位置处的波浪力,且波浪力最大点位于引堤肩台顶部附近。

图5 物模试验防浪墙前波浪力分布图Fig.5 Wave force distribution in front of wave wall by physical model test
4.4 不同方法防浪墙前波浪力结果对比
不同方法防浪墙前波浪力结果对比见表2。

表2 不同方法防浪墙前波浪力结果对比Table 2 Comparison of wave wall wave force results by different methods kN
从波浪力数值看:对于波浪水平力,国标计算结果相对于物模试验结果小约40%,英标计算结果较物模试验结果大约30%;对于波浪浮托力,国标与英标计算结果均明显大于物模试验结果。
从波浪力作用范围来看,国标计算所得波浪力作用范围明显小于英标计算及模型试验结果,结合实际的波浪爬高分析,国标计算所得波浪力的分布明显小于实际波浪力作用范围。另外,从国标波浪力计算公式组成可见,其在计算防浪墙波浪力时未直接考虑波浪周期的影响,这个是导致国标计算所得波浪力作用范围明显偏小的可能因素之一,建议在规范修订时考虑适当调整。
从波浪力大小分布情况来看,中外规范计算结果均按照波浪力在防浪墙上均布考虑,实际物模试验结果显示有护面块体掩护区域波浪力较小,无护面块体掩护区域波浪力较大,且波浪力最大点出现在肩台顶部附近,这种波浪力在防浪墙上的分布规律也得到了很多学者的试验验证[6-10]。由此可见,中外规范计算假定的波浪力沿墙身均匀分布与实际波浪作用情况存在一定偏差。
5 结语
港口航道水文规范在计算防浪墙前波浪力时,其波浪作用高度计算未直接考虑波浪周期的影响,即未对不同周期波作用下的波浪力作用高度进行区分,对于中长周期波而言,按照国标计算所得波浪力明显小于实际作用在防浪墙上的波浪力。由此,建议在按照国标进行中长周期波作用下防浪墙稳定设计时,需留有至少1 倍的安全富裕,且需通过物模试验进行断面稳定验证。此外,建议在规范更新时,对中长周期波浪下防浪墙波浪力的计算进行区别规定。
彼得森公式在计算防浪墙前波浪力时,较为充分地考虑了各个影响因素,其计算过程也相对较为复杂。但是对于中长周期波,按照彼得森公式计算所得波浪爬高往往高于防浪墙顶高程,由此导致在波浪力计算过程中荷载作用高度往往会超过防浪墙的顶标高,本文建议当波浪爬高超过防浪墙顶高程时,实际计算中取防浪墙顶高程作为波浪力作用的最高点。此外,从物模试验结果可以明显看出防浪墙前的护面块体对于防浪墙有一定的掩护作用,在根据彼得森公式进行防浪墙断层尺寸确定时,有护面块体掩护位置的波浪力可适当进行折减,避免造成设计浪费。
中外规范防浪墙波浪力计算公式基本都是通过对典型条件下的模型试验研究结果总结得到的经验公式,对于中长周期波浪作用下的防浪墙,此类计算公式计算所得结果与实际模型试验结果存在较为显著的偏差,因此,在项目施工图设计阶段,设计人员按照规范公式拟定防浪墙断面后,采用物模试验进行验证是十分必要的。
