城市输水泵站前池流态及整流措施
2018-03-06冯建刚钱向栋
冯建刚,钱向栋,张 睿
(河海大学水利水电学院,江苏 南京 210098)
城市输水泵站受城市土地限制和周围建筑物的影响,往往很难按水力条件良好的要求布置,前池易出现漩涡、回流等不良流态,水泵进水条件恶化,影响泵站的安全可靠运行[1],因此对此类泵站的前池流态进行研究十分必要。近年来随着计算流体力学和计算机技术的快速发展,数值模拟被越来越多的学者所认可,成为实际工程中研究水体流动特性的重要手段之一[2-6]。田艳等[7]采用RNGk-ε湍流模型对城市排水泵站进行全流场模拟,揭示了城市排水泵站前池内存在的复杂水流流态。对于这类布置较为局促的城市输水泵站,为改善前池流态,学者们对整流措施进行了探究。鲁俊[8]对泵站前池水力特性进行数值模拟,发现其结果与试验值相符,并提出了整流工程措施。冯建刚等[9]在上海市长江引水三期工程水源泵站的整体水力模型试验中,对底坎和八字形导流墩措施进行了比较分析。黄继宏等[10]通过分析不同导流墩参数对泵站前池水流流态的影响,明确了优化导流墩布置的相关参数。罗灿等[11]对泵站正向进水前池底坎的整流机理进行了数值模拟。然而,已有研究主要集中于单类整流措施尺寸参数对前池流态的影响,对组合式整流措施应用于城市输水泵站的研究尚不多见。本文结合某底部涵管进水形式的城市输水泵站,拟组合导流墩和底坎,探究出适用于此类泵站的整流措施。通过对泵站前池流态进行数值模拟研究,分析前池存在的不良流态及其成因,在对比分析的基础上提出改善前池流态的工程措施,并对数值模拟结果进行试验验证。
1 泵站模型的建立
1.1 泵站进水建筑物概况
泵站前池及进水池结构形式如图1所示。该泵站由进水涵管引水进入前池。前池呈平面扩散形,扩散角为20°,池底高程为-10.00 m。泵站设有3台立式斜流泵机组,编号分别为1号、2号、3号,单泵设计流量为6.21 m3/s。每台水泵均单独设进水池,以隔墩分隔,池底与前池等高。

图1 前池及进水池结构形式(单位:m)
1.2 数值模型建立
泵站前池流态处于复杂的紊流状态,雷诺数通常大于104,为不可压流动。采用RNGk-ε模型和SIMPLE算法求解流速场分布。应用雷诺时均方程,得到定常流动在笛卡儿坐标系下三维不可压缩流体的连续性方程和动量方程[12]:
(1)
(2)
式中:ui、uj(i、j=1,2,3)分别为x、y、z方向的速度分量;xi、xj(i、j=1,2,3)分别为空间坐标x、y、z;gi为沿i方向的质量力;ρ为流体密度;p为流体微元体上的压力;ν为水的运动黏性系数;νt为紊动黏性系数。
在笛卡儿坐标系下,采用Pro/E建立实体模型,利用ANSYS ICEM进行非结构化网格的划分,网格数400万左右。
进口边界设置为总压,出口边界采用质量流条件。由于前池内水面波动不大,故自由水面采用刚盖假定。壁面采用无滑移边界条件,当采用基于涡黏假设的湍流模型来封闭雷诺平均N-S(RANS)方程时,需要对近壁面流动采用特殊的处理方式。与传统的标准壁面函数相比,可伸缩壁面函数对Y+(第1层网格质心到壁面的无量纲距离)的要求并不十分严格,故计算过程中采用可伸缩壁面函数,将壁面处的物理量与湍流核心区相应物理量联系起来。
1.3 物理模型设计
物理模型按重力相似准则设计,综合考虑模型水流在阻力平方区的要求以及模型泵的选择,确定模型线性比尺λl=10。试验系统采用自循环开敞式,由取水管、前池、进水池、模型泵机组、出水管路、回水渠、控制及量测系统等组成。在前池、进水池典型断面位置布置量测水位的测压管,测压管连接测针桶,用水位测针读数,水面读数误差为±0.1 mm;在每台水泵出水管上安装超声波流量计量测水泵流量,流量计精度为0.5级,量测相对误差为±0.5%,同时每台泵分别设置量水堰槽对单泵流量进行比测,在回水渠设置量水堰量测泵站总流量;流速采用多普勒三维剖面点式流速仪(ADV)量测,ADV的精度为±1.0%,流速的相对误差为±1.0%,将进水池进口断面A作为一典型过流断面,进行流速分布的量测。流速分布量测点的布置见图2,其中水平方向上布置9条施测垂线,垂线方向上从池底到水面分5层布置。
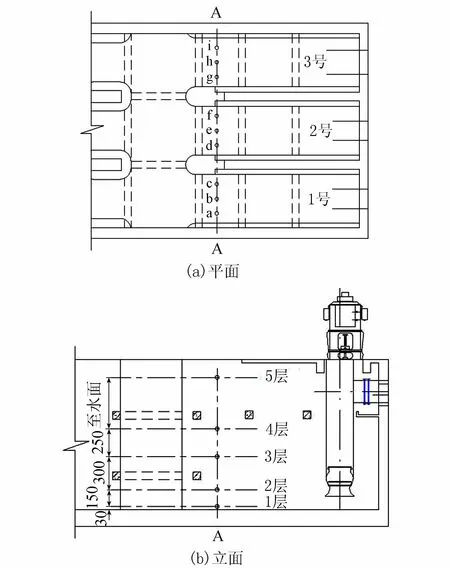
图2 流速测点布置示意图(单位:mm)
2 泵站前池流态数值模拟
2.1 前池典型截面的选取
平面上,选取泵喇叭口入口截面(对应高程-8.90 m)作为典型截面;立面上,选取3号泵管直径所在截面作为典型截面。典型截面示意图见图3。

图3 前池典型截面示意图
2.2 前池进水流态分析
结合输水泵站运行特点,将设计高水位的运行工况作为研究对象。该工况为3泵全开,前池水位为1.70 m。以典型截面的速度矢量图反映无整流措施时的前池流态,如图4所示。

图4 无整流措施时的前池流态
根据模拟结果,在平面上,主流居于中间,前池两侧产生脱壁回流且回流区的大小与扩散段长度几乎相等;进水池流量分配不均,两侧进水池进流较少。在立面上,前池表面有大尺度的回流现象,进水池底部流速很大,同时中上层有多个漩涡存在。造成前池不良流态的主要原因是有压涵管进水,主流集中且贴于前池底部,流速较大,虽然该泵站前池扩散角较小,扩散段较长,水流在前池仍得不到充分的调整。
3 泵站前池流态整流措施
3.1 八字形导流墩整流措施
3.1.1 布置形式
导流墩通过其导流作用,减小前池平面扩散角,均化水流,能够有效消除脱壁回流、偏流等不良流态。该泵站进水居中,前池两侧存在大尺度回流,进水池流量分配不均,故导流墩整流措施需在能有效调整流量分配的同时消除回流现象。这里参照冯建刚等[13]的研究成果,将八字形导流墩布置在涵管出口处,墩头与出口距离D=2 m,墩长L=8 m,两墩的夹角α=24°,后墩头正对第2排结构柱的中心,墩子高度与第2层横梁底部平齐,如图5所示。

图5 八字形导流墩整流措施布置形式(单位:m)
3.1.2 前池进水流态分析
从图6可知,采用八字形导流墩整流措施后,涵管出口密集居中的主流受导流墩作用,向两边分流,并在扩散段不断地向两侧扩散,前池两侧有了来流的补充,使得回流区近乎消失,回流现象得到明显抑制;经过较长的扩散段扩散后,流量分配得到了一定程度的调整,3个进水池流量大致相同,但各进水池流速分布均匀性较差,主要表现为各流道均存在偏流现象。在立面上,流态没有得到明显的改善,前池表层大尺度回流仍存在,进水池底部流速仍较大。
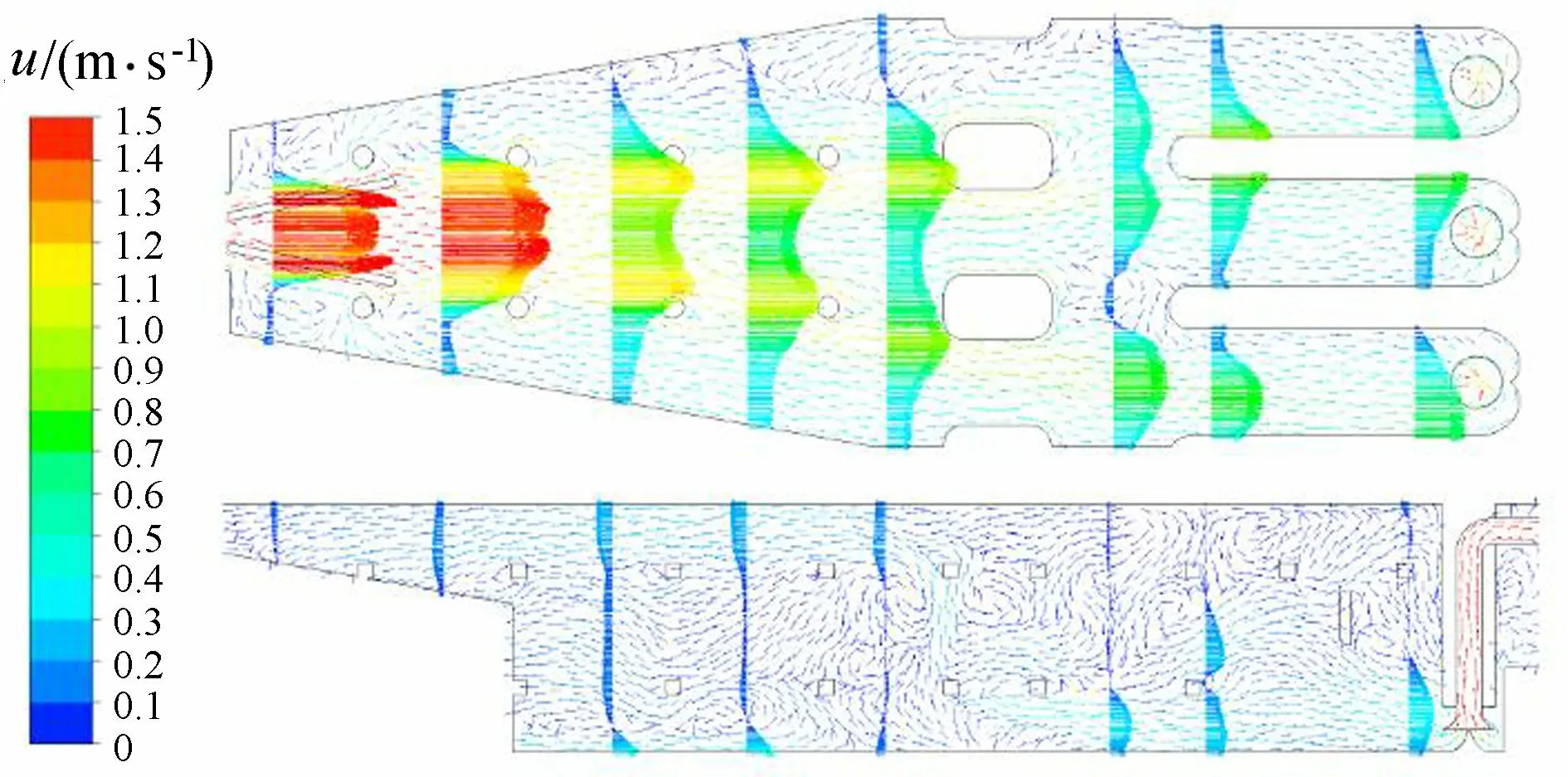
图6 采用八字形导流墩整流措施后的前池流态
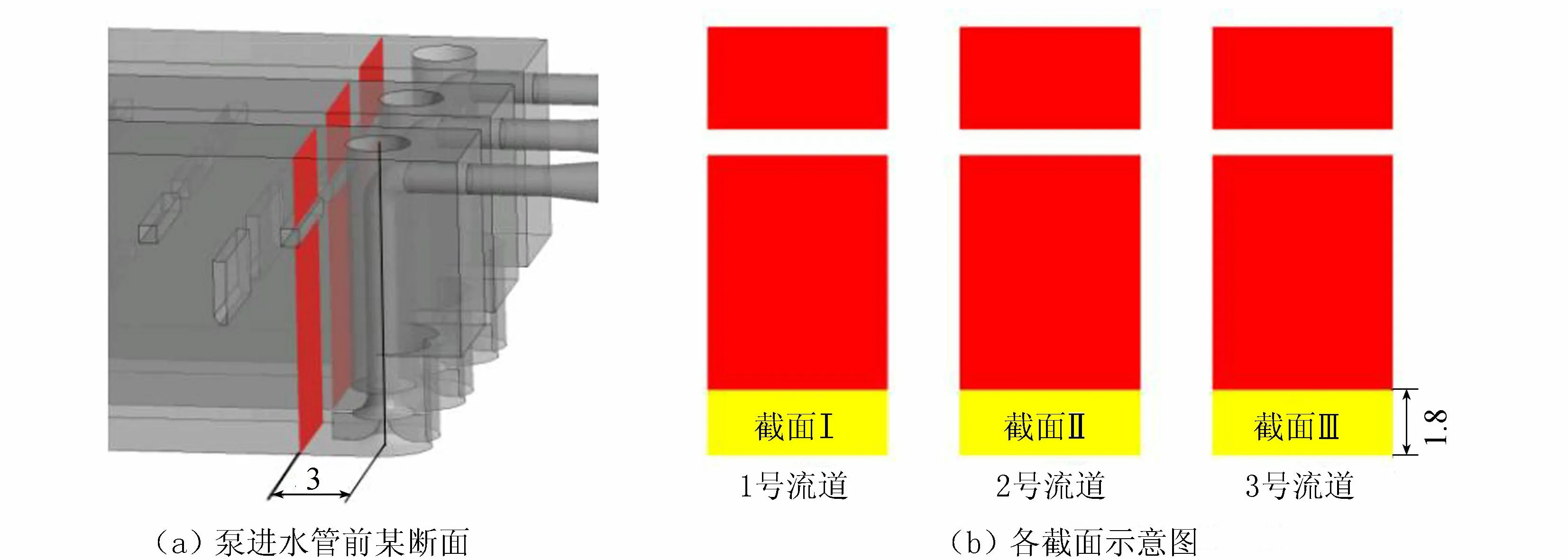
图7 所选断面和各截面示意图(单位:m)

图8 采用八字形导流墩整流措施整流前后各进水流道所选断面轴向速度云图
3.1.3 泵进水条件分析
在泵进水管前取一断面,如图7(a)所示,断面与泵管轴心在x方向的距离为3 m,分析该断面轴向速度云图,直观地比较泵进水状况的优劣;同时,在该断面上取3个等高同宽的截面Ⅰ、Ⅱ和Ⅲ,如图7(b)所示,截面的高度为1.8 m,所在区域正对泵喇叭口进水区域,分别计算各个截面的法向流速分布均匀度Vnu,计算公式[14]为

图8是前池水位为1.70 m时整流前后各进水流道所选断面轴向速度云图。整流前,由于主流居中偏下,泵进水的最大流速值出现在中间机组,相对而言,两边机组进水流速要小得多;采用八字形导流墩整流措施后,中间机组进水流速明显变小,3台泵进水平均流速大致相等。但各进水流道进水流速分布不均,偏于某一边。比较表1中整流前后各截面法向流速分布均匀度,发现采用八字形导流墩整流措施后,3个截面的法向流速分布均匀度均下降了20%左右,可见泵喇叭口进水流速分布均匀性较整流前变差。

表1 八字形导流墩方案整流前后各截面法向流速分布均匀度
3.2 组合式整流措施
3.2.1 布置形式
在有压涵管出口布置八字形导流墩,能有效地将密集的主流向前池两侧分流,消除回流区,且3个进水池流量分配大致相同,但每个进水流道均存在偏流现象,泵喇叭口进水流速分布均匀性变差。单一的八字形导流墩措施并不能有效解决城市输水泵站有压涵管进流存在的不良流态问题,需另加整流措施。底坎的整流机理是人为地制造坎后立面漩滚,破坏平面回流,使坎后流态得到重新调整,整流效果明显,同时底坎结构简单,施工简便[15-17]。
组合式整流措施是在涵管出口处布置八字形导流墩的基础上,在前池适当位置同时布置底坎。根据前池典型截面速度矢量分布和进水流道所选断面轴向速度分布制定出多个初步布置方案:将底坎布置在位置一、位置二或位置三(每个位置的间距S=2.5 m),底坎的坎高H设定为1 m、1.2 m或1.4 m,底坎宽度B设为0.7 m,如图9所示。经过数值计算结果的分析比较,发现将底坎布置在位置一时,由于其离八字形导流墩较近,导流墩的扩散作用被弱化,主流变得居中;布置在位置三时,坎后漩滚区域延伸至进水流道前,流态来不及得到充分调整。坎高H=1 m时,整流效果较H=1.2 m时差;坎高H=1.4 m时,挑流现象较为明显,造成表面流速较大。因此最终确定底坎的布置方案为底坎布置在位置二,宽度B=0.7 m,坎高H=1.2 m。
3.2.2 前池进水流态分析
采取组合式整流措施后,由于底坎的作用,使得主流在坎后发生立面漩滚,流速得到再分布。从图10可知,在平面上,坎后有一回流区,这是坎后立面漩滚造成的,过了漩滚区后,流速分布较均匀;进水池流量分配大致相同,且每个进水流道流速分布较均匀,不存在明显的偏流现象。在立面上,坎前主流收缩,水流偏向自由表面[18],原方案(导流墩方案)前池表面的大尺度回流被扰乱,回流现象得到一定程度的抑制;进水池底部流速明显减小,泵喇叭口前流速分布趋于均匀。
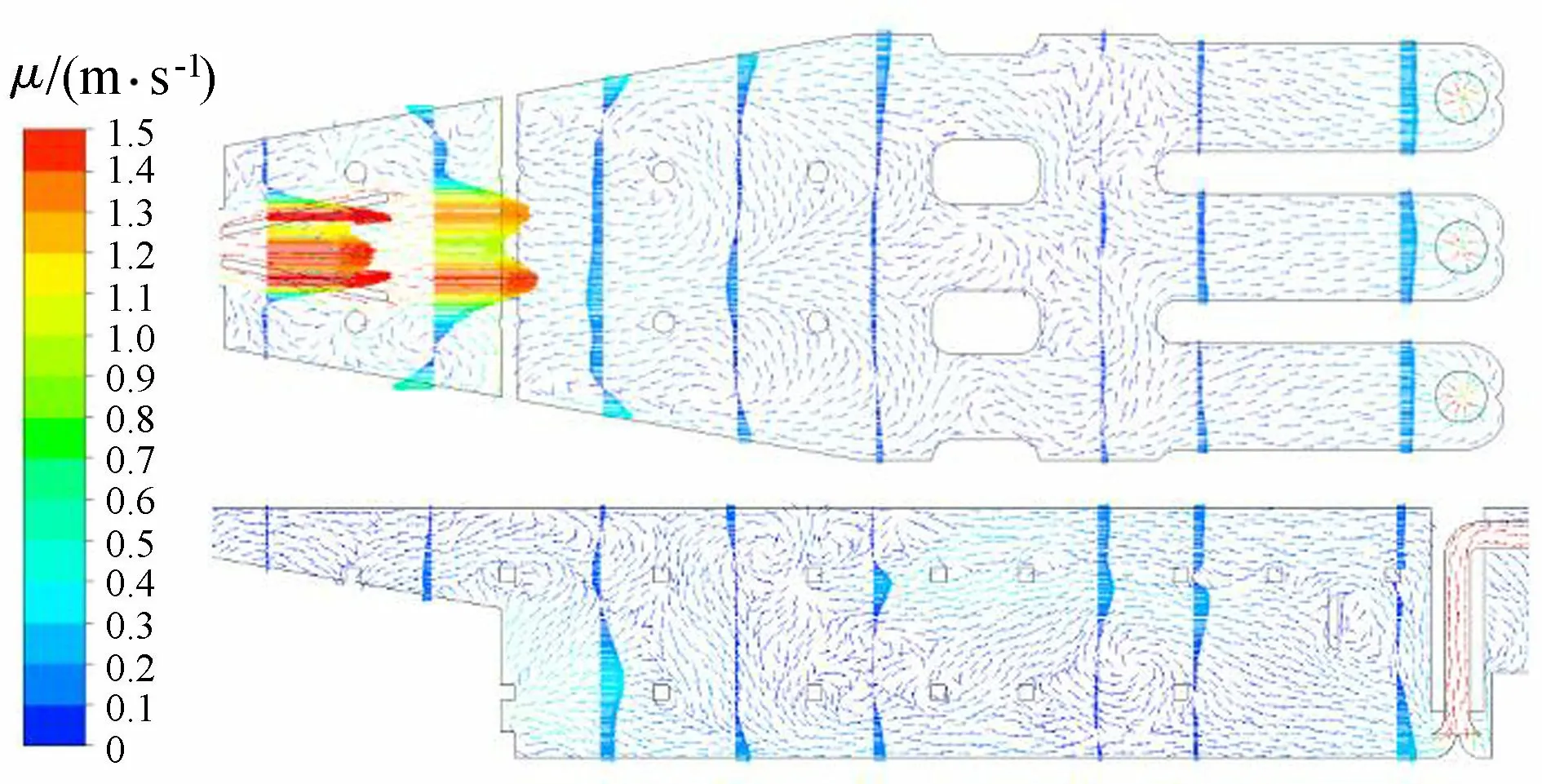
图10 采用组合式整流措施后前池流态
3.2.3 泵进水条件分析
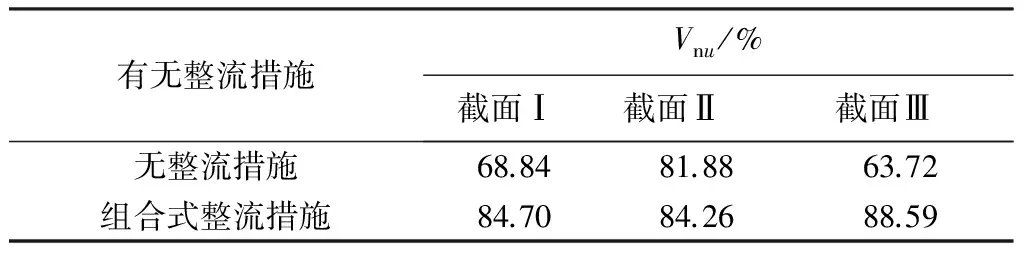
图11是无整流措施和采用组合式整流措施后各进水流道所选断面轴向速度云图。比较后发现,采用组合式整流措施后,3个进水流道流量分配大致相同,断面的流速最大值明显减小。从表2可知,采用组合式整流措施后,截面Ⅰ和截面Ⅲ的法向流速分布均匀度提高明显,截面Ⅱ的法向流速分布均匀度也有略微提高,总体上每台泵进水流速分布均匀性均较高,且2台边机组的进水条件有了较大改善。

图11 采用组合式整流措施整流前后各进水流道所选断面轴向速度云图
有无整流措施Vnu/%截面Ⅰ截面Ⅱ截面Ⅲ无整流措施68.8481.8863.72组合式整流措施84.7084.2688.59
4 试验验证

图12 物理模型前池流态

图13 进水流道典型断面流速计算值与测量值
模 型各层测点平均流速/(m·s-1)1层2层3层4层5层数值模型0.120.160.140.130.08物理模型0.160.190.120.100.07
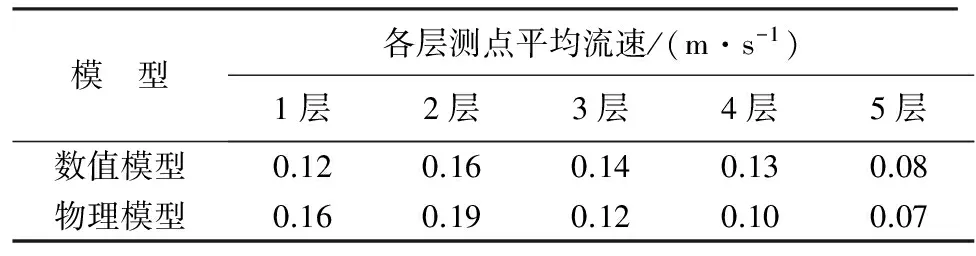
为验证数模计算结果的可靠性,进行了泵站物理模型试验。通过示踪粒子来观测前池流态,并对典型过流断面流速分布进行了测量。选取采用组合式整流措施后3泵全开的工况,前池流态如图12所示,进水池典型过流断面x方向(由管涵向进水池方向)流速计算值与测量值见图13。对比图13(a)(b)发现,计算值与测量值总体变化范围均在0.04~0.23 m/s之间,但计算值每一层不同立面间流速变化幅度稍大。将典型过流断面每一层的平均流速计算值和测量值统计入表3,发现平均流速的最大值均出现在第2层,分别为0.16 m/s和0.19 m/s;最小值均出现在第5层,分别为0.09 m/s和0.07 m/s。总体上,典型过流断面每一层的平均流速计算值和测量值大小较相近,变化趋势呈现一致性,由此可见,上述数值计算方法可行,整流措施优化研究结果可信。
5 结 论
a. 城市输水泵站布局较为局促,往往很难按水力条件良好的要求布置,进流在前池扩散段难以得到充分扩散和调整,前池两侧存在大尺度回流现象,进水池进流流量分配不均,水泵进水条件较为恶劣。
b. 前池内增设八字形导流墩和底坎的组合式整流措施,能显著改善前池流态,有效消除前池两侧回流,坎后流态重新调整,各进水池流量分配大致相同,流速分布均匀且平稳,水泵进水条件良好。
c. 流速的数值模拟计算值与物理模型测量值大小相近,变化趋势一致,表明采用数值计算方法研究泵站前池整流是可行的,数值计算结果可信。
[1] 徐辉,张林.侧向进水泵站前池整流技术研究综述[J].水利水电科技进展,2008,28(6):84-88.(XU Hui,ZHANG Lin.Review of flow pattern modifying technology for pump sump with side-inlet[J].Advances in Science and Technology of Water Resources,2008,28(6):84-88.(in Chinese))
[2] 罗灿,钱均,刘超,等.非对称式闸站结合式泵站前池导流墩整流模拟及试验验证[J].农业工程学报,2015,31(7):100-108.(LUO Can, QIAN Jun, LIU Chao, et al. Numerical simulation and test verification on diversion pier rectifying flow in forebay of pumping station for asymmetric combined sluice-pump station project[J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(7):100-108.(in Chinese))
[3] 成立,祁卫军,罗灿,等.Y形导流墩几何参数对泵站前池整流效果的影响[J].水利水电科技进展,2014,34(1):68-72.(CHENG Li,QI Weijun,LUO Can, et al. Effect of geometric parameters of Y-shaped diversion piers on flow pattern in forebay of pumping station[J].Advances in Science and Technology of Water Resources,2014,34(1):68-72.(in Chinese))
[4] 戎贵文,袁岳,肖柏青,等.局部断面收缩的溃坝水流三维数值模拟[J].水利水电科技进展,2015,35(6):20-25.(RONG Guiwen,YUAN Yue,XIAO Baiqing, et al.Three-dimensional numerical simulation of dam-break water flow with local cross-section reduction[J].Advances in Science and Technology of Water Resources,2015,35(6):20-25.(in Chinese))
[5] 周大庆,郭优,姜德政.基于桨叶调节的轴流转桨式水轮机模型飞逸数值模拟[J].水利水电科技进展,2016,36(4):13-19.(ZHOU Daqing,GUO You,JIANG Dezheng.Numerical simulation of runaway transients of kaplan turbine model based on blade regulation[J].Advances in Science and Technology of Water Resources,2016,36(4):13-19.(in Chinese))
[6] 向小华,吴晓玲,牛帅,等.基于显式有限体积法的一维河网模型[J].水利水电科技进展,2015,35(4):6-9.(XIANG Xiaohua,WU Xiaoling,NIU Shuai, et al.Construction of one-dimensional river network model based on explicit finite volume method[J].Advances in Science and Technology of Water Resources,2015,35(4):6-9.(in Chinese))
[7] 田艳,杨平,鲁俊.城市排水泵站前池流态的数值模拟研究[J].水泵技术,2008(4):24-26.(TIAN Yan, YANG Ping, LU Jun. Numerical simulation of flow patterns in forebays of the urban drainage pumping stations[J].Pump Technology,2008(4):24-26.(in Chinese))
[8] 鲁俊.城市排水泵站前池整流技术CFD研究[D].南京:河海大学,2006.
[9] 冯建刚,李杰.大型城市水源泵站前池流态及改善措施试验[J].水利水电科技进展,2010,30(2):70-74.(FENG Jiangang,LI Jie.Flow patterns in forebays of large urban water source pumping stations and countermeasures[J].Advances in Science and Technology of Water Resources,2010,30(2):70-74.(in Chinese))
[10] 黄继宏,王晓升,张晓毅.城市排水泵站前池导流墩整流措施的数值模拟[J].江苏农业科学,2013,41(5):360-362.(HUANG Ji Hong, WANG Xiao Shen, ZHANG Xiao Yi. Numerical simulation of rectification measures of diversion pier in the forebay of urban drainage pumping stations[J].Jiangsu Agricultural Sciences,2013,41(5):360-362.(in Chinese))
[11] 罗灿,成立,刘超.泵站正向进水前池底坎整流机理数值模拟[J].排灌机械工程学报,2014,32(5):393-398.(LUO Can, CHENG Li, LIU Chao. Numerical simulation of mechanism for sill rectifying flow in pumping station intake[J].Journal of Drainage and Irrigation Machinery Engineering,2014,32(5):393-398.(in Chinese))
[12] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2007:114-126.
[13] 冯建刚,王晓升,佟宏伟,等.大型城市供水泵站前池流态改善措施研究[J].给水排水,2010,36(11):51-54.(FENG Jiangang,WANG Xiaosheng,TONG Hongwei, et al. Improving of the flow patterns in forebays of the large urban water supply pumping stations[J].Water & Wastewater Engineering,2010,36(11):51-54.(in Chinese))
[14] 李坦,靳世平,黄素逸,等.流场速度分布均匀性评价指标比较与应用研究[J].热力发电,2013,42(11):60-63.(LI Tan,JIN Shiping,HUANG Suyi, et al. Evaluation indices of flow velocity distribution uniformity: comparison and application[J].Thermal Power Generation,2013,42(11):60-63.(in Chinese))
[15] 周大庆,刘跃飞.基于VOF模型的轴流泵机组起动过程数值模拟[J].排灌机械工程学报,2016,34(4):307-312.(ZHOU Daqing,LIU Yuefei.Numerical simulation of axial pump unit startup process using VOF model[J].Journal of Drainage and Irrigation Machinery Engineering,2016,34(4):307-312.(in Chinese))
[16] 张琳,施卫东,张德胜,等.基于大涡模拟的混流泵不稳定流动数值研究[J].排灌机械工程学报,2017,35(4):303-308.(ZHANG Lin,SHI Weidong,ZHANG Desheng,et al. Analysis of instability flow on mixed-flow pump based on LES[J].Journal of Drainage and Irrigation Machinery Engineering,2017,35(4):303-308.(in Chinese))
[17] 成立,刘超,周济人,等.泵站前池底坝整流数值模拟研究[J].河海大学学报(自然科学版),2001,29(3):42-45.(CHENG Li, LIU Chao, ZHOU Jiren, et al.Numerical simulation of sill flows in the forebay of pumping station[J].Journal of Hohai University(Natural Sciences),2001,29(3):42-45.(in Chinese))
[18] 冯旭松.泵站前池底坎整流及坎后流动分析[D].扬州:扬州大学,1996.
