小球重力瞬时功率取极值时相应位置的探讨
2018-03-06邹兆贵
邹兆贵
(湖南省长沙市长郡滨江中学,湖南 长沙 410013)
在高中物理当中,功与能是非常重要的概念.在对功的学习当中,经常会遇到求物体瞬时功率的问题.往往涉及物体受到的某个力的瞬时功率如何变化,在何位置取极值,以及极值是多少等问题,既考查了学生对瞬时功率公式本身的掌握与应用,也考查了学生的定性、定量分析物理过程的能力,同时也为后续动能定理的学习打下扎实的基础.以下就小球重力瞬时功率如何变化及取极值时相应位置进行探讨.
1 问题
如图1,图2所示,质量为m的小球从水平位置A静止释放,小球从水平位置A运动到最低点B点的过程中,重力的瞬时功率如何变化?在何处最大?(忽略空气阻力及小球的体积)

图1 “球绳模型” 图2 “球绳模型”过程分析图
2 问题分析与解答
2.1 定性分析
设绳长为L,当小球运动到C点时,速度为vC,距离A竖直高度差为h,绳子与水平方向的夹角为θ,运动到最低点B点时,速度为vB.
由题易知vA=0,则PA=0 W,又
而PC=mgvCcosθ>0 W,
故从A到B的过程中,重力的瞬时功率从0先增大,后减小到0.
2.2 定量分析
当小球运动到C点时,由几何关系知
h=Lsinθ.
(1)
由动能定理得
(2)
解得
(3)
把(3)代入PC=mgvCcosθ得
(4)

下面通过不同的方法来求PC的最大值及对应的位置.
2.2.1 均值不等式法[1-2]
f4(θ)=sin2θcos4θ=sin2θcos2θcos2θ=
(5)


2.2.2 导数法[3-4]
则g′(θ)=cosθ(3cos2θ-2).
令g′(θ)=0得到
由数学易知
故g(θ)逐渐增大,PG逐渐增大.
故g(θ)逐渐减小,PG逐渐减小.

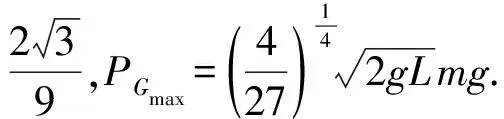

3 进一步探讨
如果与小球连接的物体不是绳子,而是光滑半圆槽,同时槽对小球的弹力对小球做功,此时小球重力的瞬时功率变化情况又会如何?
3.1 新问题
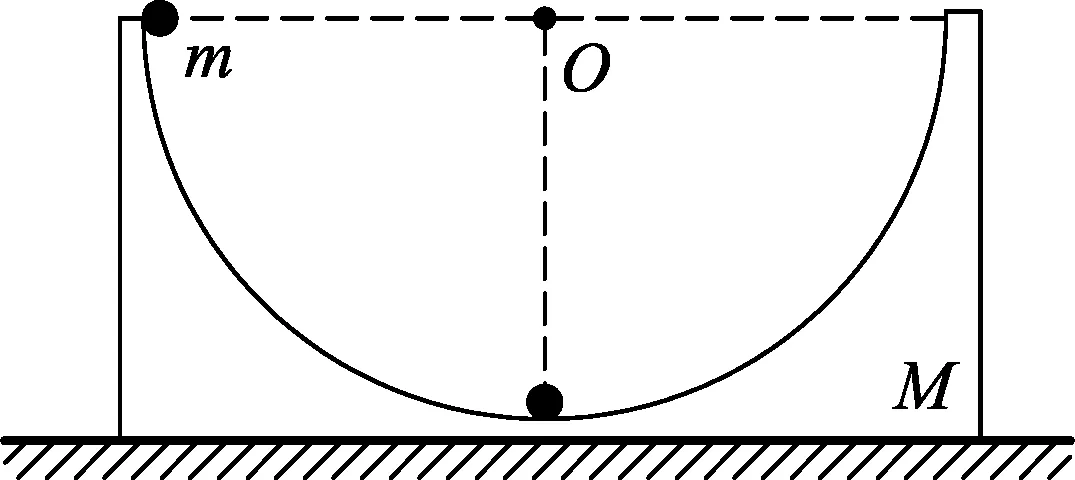
图3 “球槽模型”图
如图3所示,质量为M的光滑半圆槽静止置于光滑水平地面上(半圆槽不固定),一质量为m的小球位于槽内,从与圆心O等高的水平位置静止释放,求小球从静止释放到运动到槽内最低点的过程中,小球重力瞬时功率如何变化?最大值在何处?(小球的大小可以忽略)
3.2 理论分析与解答[7-8]

图4 “球槽模型”过程分析图
如图4所示.设槽的半径为R,小球与圆心O的连线与水平方向的夹角为θ时,小球速度为v1,水平速度大小为v1x,竖直速度大小为v1y,槽的水平速度为v2,小球相对于槽的速度为v3.
对M、m系统,由机械能守恒定律得
(6)
由系统水平动量守恒可得
mv1x=Mv2.
(7)
由几何关系易知
v1x+v2=v1ytanθ.
(8)
对m:
v1x2+v1y2=v12.
(9)

由系统机械能守恒定律易知,小球下滑过程中,槽对小球的弹力对小球做负功.
小球的瞬时功率为
PGm=mgv1y=
(10)
化简(10)式得

(11)

再令
A=k(k+1)+(k+1)2cot2θ.
(12)
把(12)式代入(11)式并对h(θ)求导得
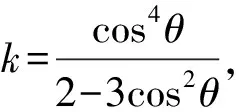
令cos2θ=t,t∈[0,1]代入上式得





图5 k取不同值时,h(θ)随θ变化图像
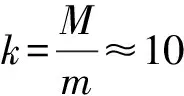
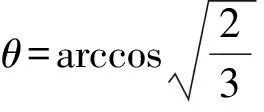
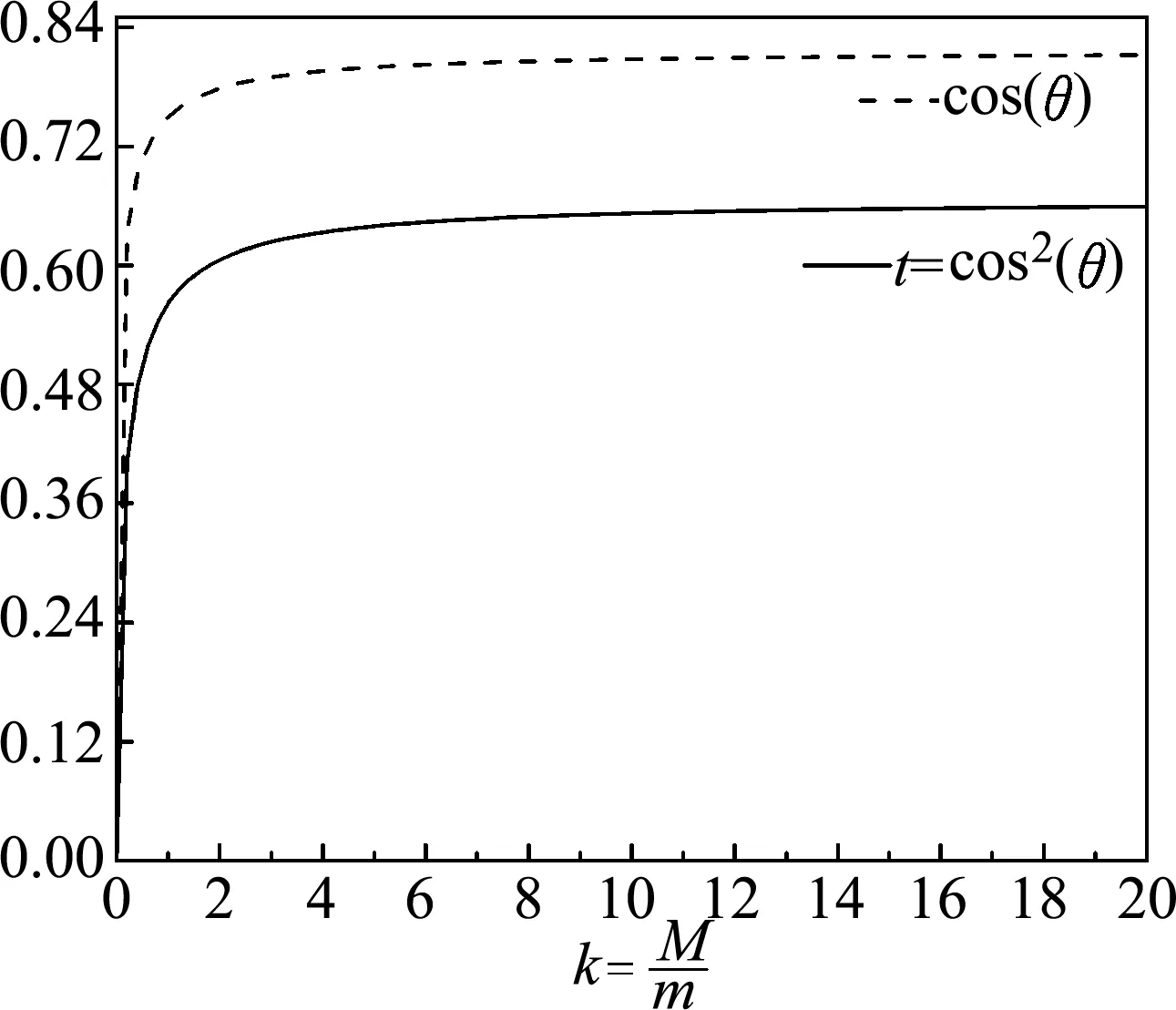
图6 h′(θ)=0对应的cos及cos2(θ)随k变化图像
4 结束语
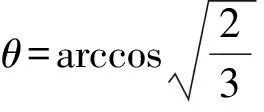

两种模型虽有区别,但也有共同点.通过理论分析与数值计算同时借助软件Origin绘图,直观的显示了小球重力的瞬时功率变化规律及极值位置.
值得注意的地方:当k很小时,槽相对小球质量很轻,有可能会翻转,因为涉及到转动的问题不在高考范围之内,且更为复杂,本文不再予以讨论.
