一道基于镜像法对电场的严格求解问题
2018-03-06黄志豪张冠中
黄志豪 张 雪,2 李 轩 张冠中
(1.东北师范大学物理学院,吉林 长春 130024;2.郑州市第四十二中学,河南 郑州 450000)
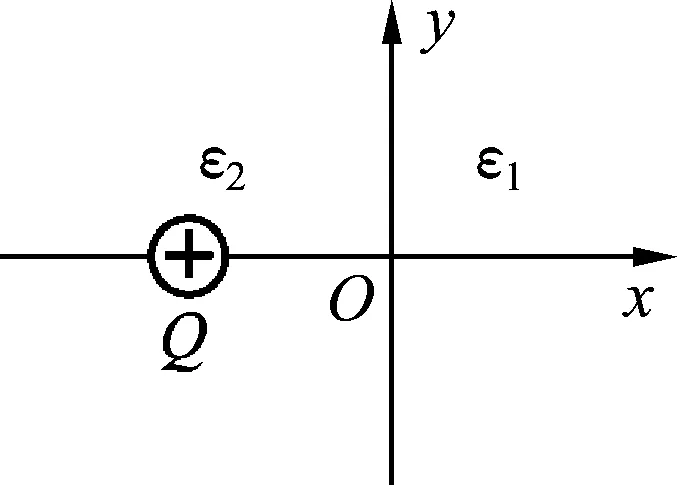
图1
如图1所示,x>0和x<0区域分别充满电容率ε1和ε2的各向同性线性介质,x<0区域有一点电荷Q,它到分界面x=0的距离为d(d<0),求各区域的电场分布.
文献[1]将上文作为例题促进学生对镜像法一节的理解,随后在解题步骤中根据唯一性定理设出“像点荷的大小为q′,位置x=-d”作为条件进行求解,这是典型的“尝试法”解题思路.尽管最后结果正确,但由于解题过程不甚严格,导致部分学生对其理解存在困难,同时也不利于学生对镜像法基本思想的准确把握,甚至有部分学生产生了“利用镜像法求解场方程表达式一般不可准确求解”的错误思想.本文提出了一种严格求解的方法得到场方程表达式,并作出相互正交的等势线和电场线簇图形,讨论了分界面两侧介质电容率之比对图形的影响.
1 场问题的严格求解
记x>0区域电势为φ1,x<0区域电势为φ2.
定义
首先对x>0区域电势分析,根据唯一性定理,可设像点荷为Q′(a,0,0)(a<0).则x>0空间任一点电势可表示为
(1)
对于x<0区域电势,同理可设像点荷电量为Q′(b,0,0)(b>0).则x<0空间任一点电势可表示为
(2)
根据边值关系,分界面x=0上有
φ1|x=0=φ2|x=0.
(3)
(4)
即
(5)
(6)
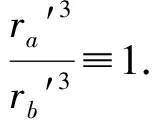
a=-b,Q′=-Q″.
(7)
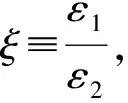
(8)
同理可得Q″=ηQ,Q′=-ηQ,a=-b=d,即
a=-b=d,ra=rd,ra′=rb′=rd′.
(9)
(10)
利用E=-φ得电场强度
(11)
(12)
式(11)所得结果和尝试法所得结果完全一致,证明本文严格求解的方法是正确的.
2 电场线和等势线簇图形
为简单起见,考虑到Q为固定值,则可将等势线簇函数表示为
(13)
(14)
电场线簇函数为
(15)
(16)
研究ξ对z=0面等势线和电场线簇图形的影响,作出对应的等势线和电场线簇图形,如图2所示.
设定参数:点电荷坐标Q(-1,0,0),介质电容率之比分别为ξ1=15、ξ2=5、ξ3=1、ξ4=0.05.

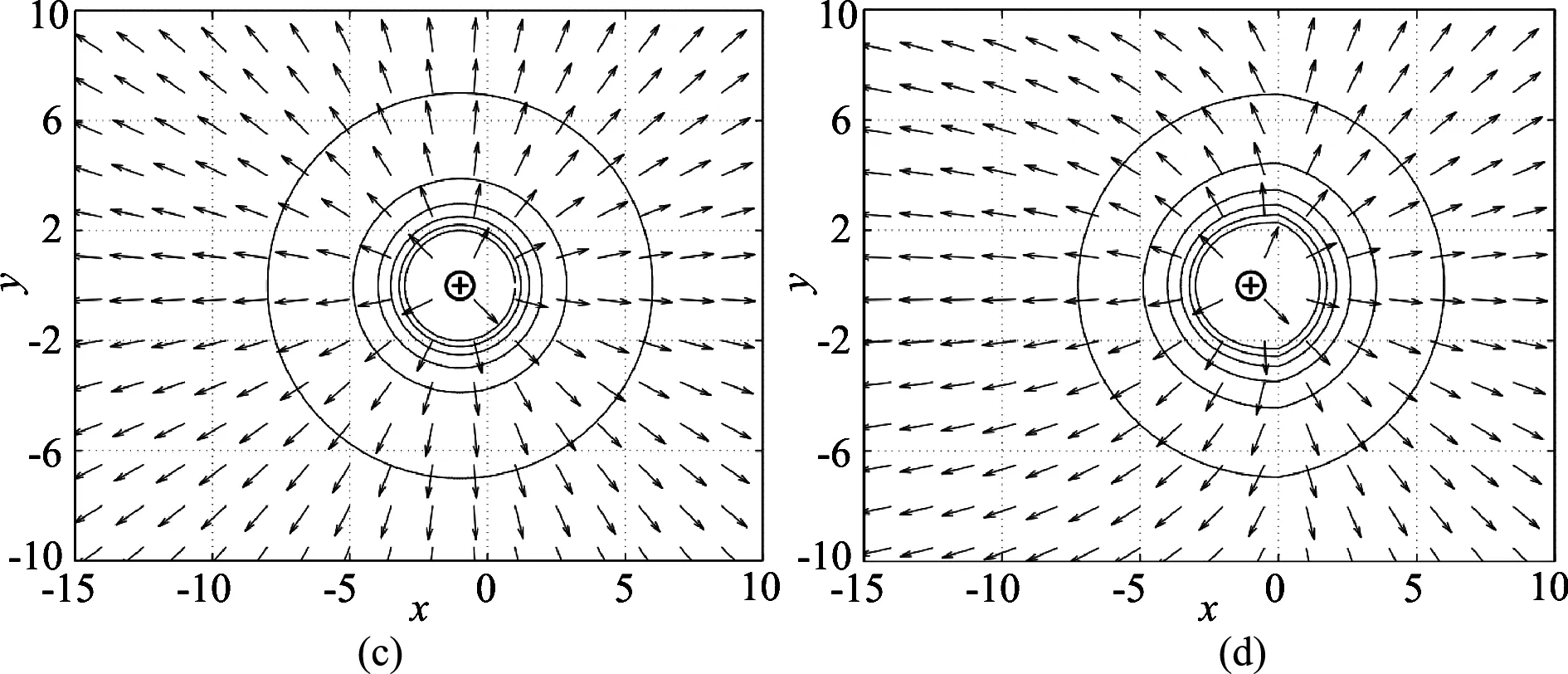
图2 z=0平面不同ξ值下电势电场正交簇图形
(图aξ1=15; 图bξ2=5; 图cξ3=1; 图dξ4=0.05)
由图可知,每处箭头方向代表电场方向,电势电场关于y轴对称分布,这与带电体关于y轴对称有关,带电体的对称性决定了它所激发电场的对称性.此外,根据坐标轴的旋转不变性,可以推测,y=0平面和z=0平面的等势线和电场线簇图形一致.ξ的大小对正交簇图形有一定的调制作用.以ξ=1为界,当ξ>1时,随着ξ逐渐减小,分界面两侧图形逐渐趋于一致,表现为: (1) 同一条等势线关于x=-1对称的区段对应的曲率逐渐趋于一致,电场取向趋于一致; (2) 同一条等势线与x=-1所围图形左右两侧面积大小趋于一致.ξ=1时,图形和一放置在线性均匀介质中的点电荷所产生的电势电场簇图形相同.0<ξ<1时,ξ对两侧图形的调制作用减弱. 同时也应该看到,模拟图像中(1,0,0)处,即像点荷位置,出现无电势电场分布的奇点,表明镜像法不能用来求解像电荷所在区域.
3 结论
本文灵活运用常量变量之间所应满足的对应关系,对场函数表达式进行了严格求解,有利于加强学生对镜像法的理解.作出相互正交的等势线和电场线簇图形,得出电容率比值在不同区间对电势电场正交簇图形的调制作用效果不同.
