基于极坐标的特殊结构零件数控编程的研究与应用*
2018-03-06谢仁华管嫦娥
谢仁华,管嫦娥
(江西应用技术职业学院 机电学院,江西 赣州 341000)
在数控编程中,目标点的坐标通常采用直角坐标来表示[1]。而对于一些具有特殊结构的零件,其结构尺寸主要由角度值及半径值组成,如果采用直角坐标系编程,就需要用三角函数进行繁琐的计算,若采用极坐标系编程,就能很好地利用极径(即半径值)和极角(即角度值)来编程,从而避免复杂的计算,简化数控编程,提高编程效率,提升加工精度,具有很强的现实意义。
1 极坐标系定义
极坐标系的示意图如图1所示。通过平面内任意一点O,作一条水平射线OX,O点称为极点,水平射线OX称为极轴,这样就建立了一个极坐标系[2]。平面内任意一点P,与极点O的连线OP称为极径。θ角称为极角,是极径与极轴的夹角,逆时针方向用正值表示,如P(ρ,θ);顺时针方向用负值表示,如P(ρ,-θ)。可见,利用极坐标的极径与极角,可以很方便地描述平面内任意一点的位置。
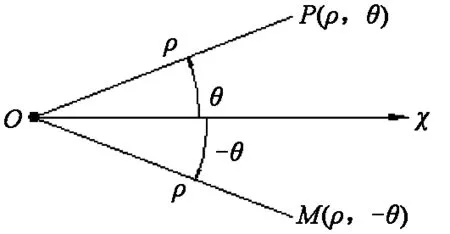
图1 极坐标系的示意图
2 极坐标编程指令
以FAUNC系统为例,极坐标编程指令如下:
G17/G18/G19 G16;
G00/G01(G02/G03)X_ Y_(R_)F_;
…
G15;
程序中,G17/G18/G19表示选择加工平面;G16表示建立极坐标,X表示极径,Y表示极角,F表示进给率;G15表示取消极坐标,一般单独列一行。
3 极坐标在特殊结构零件中的应用
3.1 极坐标在腰形槽零件中的应用
腰形槽零件结构如图2所示。腰形槽结构是一种特殊的封闭槽类结构,所有的结构都由圆弧连接组成。如果采用普通的直角坐标系编程,图2所示的3、4、5、6点的x、y坐标值都要用正弦和余弦函数来计算。以3点为例,x=-19cos45°,y=19sin45°,计算相当繁锁,且会增加误差。此外,由图样可知,腰形槽结构尺寸主要由半径和角度组成,所以如果采用极坐标编程,就省去了复杂的计算,程序也变得简单。
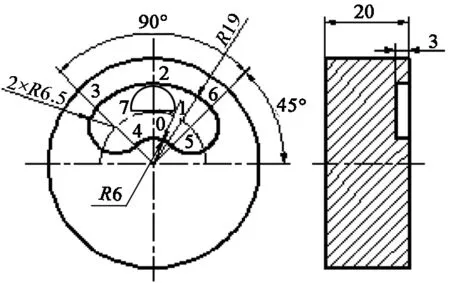
图2 腰形槽零件
腰形槽零件的数控铣削加工程序如下:
O0301; (φ10键槽铣刀)
G54 G90 G17 G40 G0 Z100;
X0 Y12.5; (下刀点0)
M3 S1200;
G0 Z5 M8;
G1 Z-3 F50;
G1G41X6.5D01F200; (0-1建刀补)
G3 X0 Y19 R6.5; (1-2圆弧切入)
G16 G3 X19 Y135 R19; (3点建立极坐标)
G3 X6 Y135 R6.5; (4点)
G2 X6 Y45 R6; (5点)
G3 X19 Y45 R6.5; (6点)
G3 X19 Y90 R19; (2点)
G15; (取消极坐标)
G3 X-6.5 Y12.5 R6.5; (2-7圆弧切出)
G1 G40 X0 Y12.5; (7-0取消刀补)
G1 G40 Z5;
G0 Z100;
X0Y0;
M9;
M5;
M30;
3.2 极坐标在正多边形中的应用
正五边形零件如图3所示。从图3可以看出,正五边形主视图只给出了2个尺寸,一个是外接圆直径φ100,另一个是第5点同中心O连线与x轴的夹角18°。如果采用直角坐标编程,图上1、2、3、4、5点坐标值都要通过角度为已知量的三角函数值进行计算,计算繁杂且会因为数值小数点的处理造成定位误差。这种情况下若采用极坐标就可以大大简化计算,提高定位精度。
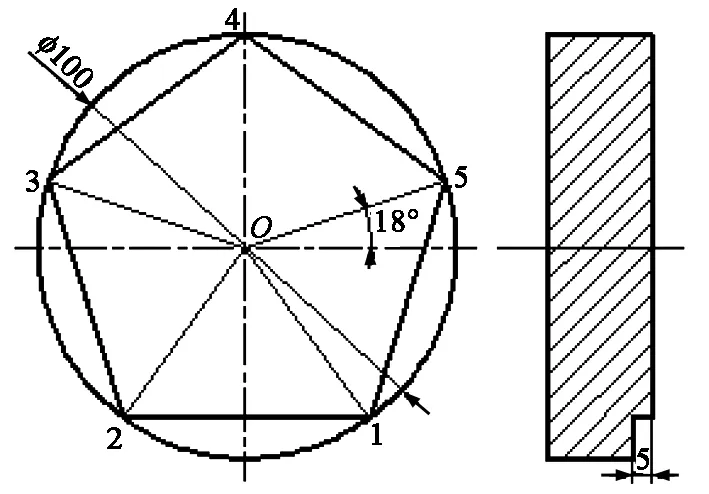
图3 正五边形零件
正五边形零件的铣削加工程序如下:
O0302; (φ12三刃立铣刀)
G54 G90 G17 G40 G0 Z100;
X65 Y-43; (下刀点)
M3 S1200;
G0 Z5 M8;
G1 Z-5 F200;
G16 G41 X50 Y-54 D1; (开始建立极坐标,并建刀补,第1点的极轴顺时针转了54°,所以极角为负值)
Y234; (第2点开始极轴逆时针旋转角度计算,所以为正值)
Y162; (第3点)
Y90; (第4点)
Y18; (第5点)
Y-54; (回到第1点)
G15; (取消极坐标)
G1G40 Z5; (取消刀补)
G0 Z100;
M9;
M5;
M30;
对于这种正多边形的结构,在生产实践中经常会遇到,编程时只要根据多边形的边数,适当变换极径及极角数值就可以使用,因此这种程序具有很强的通用性。
3.3 极坐标在圆周分布的孔群类零件中的应用
圆盘零件结构如图4所示。图4中,10个φ12的通孔沿φ60圆周均布,板材厚度为8 mm。要加工孔,首先要确定孔的中心点,如果直接利用直角坐标系中的三角函数计算中心点的坐标值,计算非常麻烦而且在计算过程中会产生误差和误差的累积,从而影响孔的定位精度。如果用极坐标,只需知道极径和极角,本例中极径都为30,角度只要简单计算即可获得,因此程序显得极为简单,而且定位精准,避免了计算误差和累积误差。

图4 圆盘零件
圆盘零件的数控加工程序如下:
O0303; (φ12麻花钻头)
G54 G90 G17 G40 G0 Z100;
M3 S1200;
G0 Z5 M8;
G16; (建立极坐标)
G99 G81 X30 Y15 Z-10 R3 F80 (钻第1个孔,钻孔深度要大于板材厚度)
Y51; (钻第2个孔,由于只有角度不同,所以只写极角)
Y87; (钻第3个孔)
Y123; (钻第4个孔)
Y159; (钻第5个孔)
Y195; (钻第6个孔)
Y231; (钻第7个孔)
Y267; (钻第8个孔)
Y303; (钻第9个孔)
Y339; (钻第10个孔)
G15; (取消极坐标)
G80;
G0 Z100;
M9;
M5;
M30;
上述程序不仅适用于圆周分布的孔类零件,而且对所有规律排列的孔阵类零件都可以灵活运用。
4 结语
通过极坐标编程在腰形槽、正五边形、圆周分布的孔群类零件中的应用实例,不难发现,巧妙应用极坐标编程能简化特殊结构零件的数控编程,减少计算量,提高编程效率,提升加工精度,对生产实践中的数控编程具有一定的指导意义[3-4]。
[1] 刘向红,刘艳申.基于极坐标的数控铣削手工编程零件加工[J].西安航空技术高等专科学校学报,2012,30(5):57-59.
[2] 刘冲,王峥.浅谈数控编程中的极坐标功能[J].数字技术与应用,2012(9):223.
[3] 宋亮.刀具补偿在数控编程中的应用[J].中国科技投资,2016(6):203.
[4] 西庆坤.基于极坐标的连续进给编程在曲面加工中的应用[J].机床与液压,2015(14):55-57.
