连续体机械臂振动特性研究

高国华， 李炼石， 夏齐霄, 王 皓， 任 晗

(1.北京工业大学机械工程与应用电子技术学院 北京，100124) (2.北京联合大学机器人学院 北京，100020)

引 言

随着机构柔顺化的不断发展，柔顺机构学相关研究逐步由部分柔性向全柔性、从刚柔耦合向全局软体进展[1-3]。连续体机构是柔顺机构学研究中的重要分支之一，其仿生性、灵活性和自适应性的优势使其渐入人们视线，并已逐步应用在医疗辅助[4]、军事救援和农业作业[5-6]等方面。

连续体机构构成的机器人主要有杆驱动[7]、气动肌肉[8]和线驱动[9]等驱动形式。在近年的研究中，以柔性杆连续体机构为主题的机器人、机械臂崭露头角，但连续体机械臂在工作中的振动是制约其应用的重要因素之一，也是重点研究方向。国内外学者通过高速摄像和光栅测距仪等非接触式传感器测量柔顺机构振动，取得了较好的效果。连续体机械臂末端振动测量主要有接触形与非接触形两种形式[10-11]。邱志成等[12]利用机器视觉采集柔性臂振动及其控制,验证了机器视觉测试的可行性。文献[13]在柔性机械手的精确定位和振动抑制的研究中,利用相位探测器与LED采集分析了其振动特性。文献[14]在运用短时傅里叶变换实时测量柔性杆振动评估的研究中，利用高速相机与IMU惯性传感器测量柔性臂振动。王辉[15]在压电柔性臂冲击振动的瞬态响应及其抑制研究中，利用压电陶瓷与压电作动器来检测与抑制柔性臂振动。张庆[16]通过加速度传感器、位移传感器验证了板簧式柔性臂夹紧力、叠层刚度和叠层层数对振动影响，为组合柔性机械臂的减振设计提供了有效思路。

连续体机械臂末端振动形式较为复杂。在不同的伸长量及不同的弯曲度下，其振动的阻尼固有频率与衰减系数是不同的，无法通过理论计算得出。为此，本研究以弹簧为脊椎，开发了脊椎可伸缩的连续体机械臂。弹簧既可以产生传统脊椎的弹性侧弯运动，又可以容易地改变脊椎长度，方便实验进行。在实验中，通过参数识别的方式确定其振动形式及动力学参数。发现末端振动的能量主要受一阶模态的影响。因此，可通过简化振动模型、测量并拟合振动曲线，获得连续体机械臂在不同位姿下对应的动力学参数。

1 实验台

实验台由连续体机械臂系统和数据采集系统两部分组成。连续体机械臂系统用于位姿调整和激发振动，数据采集系统收集并处理振动信号。

1.1 连续体机械臂系统

实验用连续体机械臂如图1所示。连续体机械臂由4根直径为2.5 mm的玻璃纤维棒与8个外径为40 mm、线径为1.5 mm、自然长度为80 mm、劲度系数K为57.65 N/m的弹簧构成。连续体机械臂分布有数个材料为铝镁合金的支撑架，外围4根柔性杆从支撑架末端孔中穿过，在孔中可自由滑动。弹簧可被压缩至30 mm，弹簧与每两个支撑架间采用固定装配，用于柔性连续体机械臂伸缩。

连续体机械臂工作时，4根玻璃纤维柔性杆固定装配在滚珠丝杠的滑块上，伺服电机驱动滚珠丝杠，使玻璃纤维棒可进行伸缩运动。位于支撑架上下两端的弹簧可以使连续体机械臂玻璃纤维棒做上下移动时，保证支撑架间距变化相同。由于支撑架的约束，连续体机械臂的弯曲形态呈圆弧状态[17]。随着外围玻璃纤维棒伸长量的变化，连续体机械臂的整体姿态会发生规律性可控变化。

笔者开发了连续体机械臂，其伸缩范围为250～700 mm，主要受所选弹簧参数和驱动单元尺寸的影响，连续体机械臂样机可在连续体机械臂长度为250 mm和700 mm时形成的心形曲面所包裹空间内运动[18]。

图1 连续体机械臂样机Fig.1 Prototype of continuum manipulator

1.2 实验流程

振动数据采集使用Mpu6050加速度传感器完成。Mpu6050加速传感器可采集三轴的线加速度、角速度以及位姿角，加速度传感器采样率为200 Hz。研究中，将传感器固定装配在连续体机械臂末端，收集连续体机械臂末端振动信号，通过STM32单片机传输至PC端。实验台如图2所示，Mpu6050固定在连续体机械臂末端并与STM32单片机连接。实验中，先将连续体机械臂调整至预设位姿，然后将连续体机械臂末端通过牵引线拉动偏移平衡位置50 mm，夹持在电磁铁控制端子处。当电磁控制端通电瞬时，牵引线被释放，连续体机械臂产生振动，其末端的振动信号通过Mpu6050采集，并通过串口通信传输至PC端进行处理，如图3所示。

图2 振动实验原理图Fig.2 Schematic of vibration experiment

图3 振动实验流程图Fig.3 Flow chart of vibration experiment

2 振动形态与参数确定

连续体机械臂在启停与快速运动过程中，不同位姿对应的刚度和阻尼比等参数均会随之变化，导致其振动形式相当复杂，目前无法在理论上建立模型。因此，本研究采用实验法与拟合模型，对连续体机械臂末端到达目标位置后振动位移情况进行研究。实验中，连续体机械臂弯曲角度θ与长度L取值范围如表1所示。研究中，θ的变化间隔为10°，L的间隔为20 mm，共取100组参数，每组实验重复5次，取平均值以降低系统误差。

表1 振动实验数组Tab.1 Array of vibration experiment

通过置于连续体机械臂末端加速度传感器采集数据如图4所示。图4所示的振动时间曲线进行快速傅里叶变换如图5所示。可以看出：连续体机械臂的一阶模态振动起主导作用，二阶模态振动的功率密度幅值很小；二阶模态振动在摩擦作用下迅速衰减，一阶模态下的振动功率密度幅值仍然很大，而二阶模态下的振动已基本消失；三阶及以上模态的振动一直被淹没在噪声中，可以忽略不计。

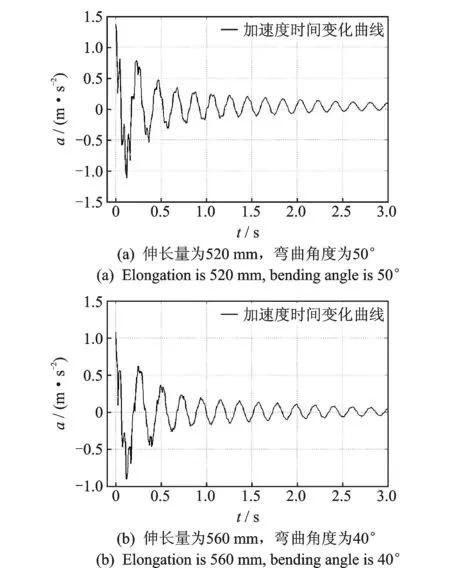
图4 加速度时间变化曲线Fig.4 Curve of acceleration

图5 不同周期幅频特性曲线变化Fig.5 The amplitude-frequency curve of different periods

图6为不同位姿下幅频特性曲线变化。可见，连续体机械臂的弯曲角度越大，一阶与二阶模态振动的频率越高，其变化规律如图7(a)，(b)所示。在弯曲角度相同时，伸长量越大，一阶与二阶模态振动的频率越低，其变化规律如图7(c)，(d)所示。由于高阶模态振动的功率密度幅值相对一阶模态振动很小，且在一阶振动的两周期后基本消失，因此在实际减振规划中只考虑连续体机械臂末端在一阶模态下的阻尼振动。

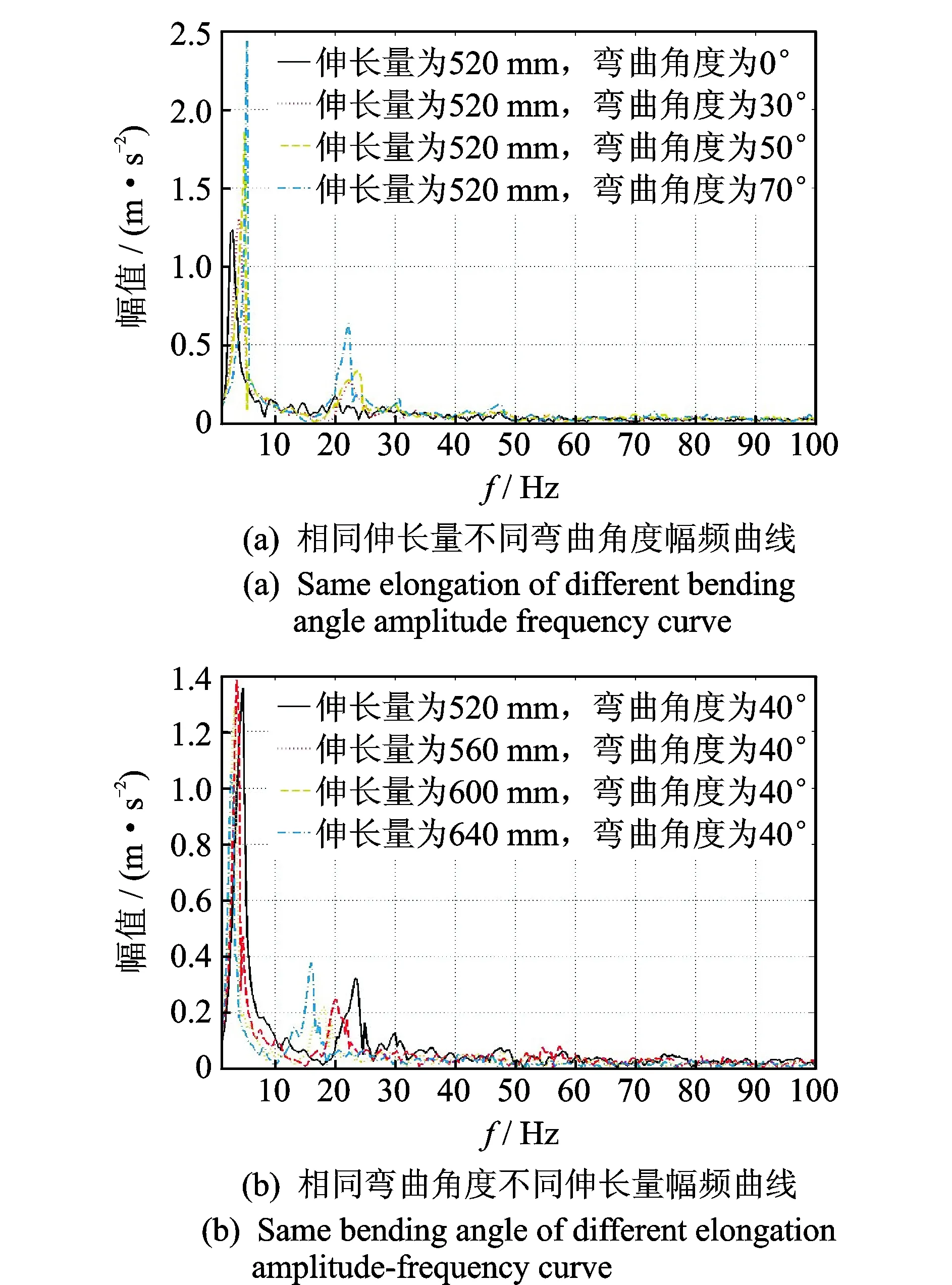
图6 不同位姿下幅频特性曲线变化Fig.6 The amplitude-frequency curve

图7 不同位姿下频率变化曲线Fig.7 The frequency variation curve of different positions

2.1 振动实验参数的定义

为了便于理解所提出的理论，定义表2所示参数，如图8所示。

表2 实验相关参数定义Tab.2 Definition of experiment related parameters

图8 连续体机械臂示意图Fig.8 Schematic diagram of flexible continuous manipulator

由于连续体机械臂末端振动在一阶阻尼振动由第2周期后起主导作用，故可针对其一阶阻尼振动进行研究，其运动理论模型设为

s=Ae-σtsin(ωdt+τ)

(1)

由于采用加速度传感器进行测量，需将式(1)对时间求二阶导数，得到连续体机械臂末端加速度关于时间t的关系式为

(2)

振幅A与初相角τ可由连续体机械臂末端到达目标位置时初始条件确定，根据阻尼振动公式，表示为

(3)

2.2 连续体机械臂末端振幅的确定

2.3 连续体机械臂末端速度的确定

连续体机械臂十字支架的限位，认为其弯曲方式为常曲率的纯弯曲形式，利用纯弯曲的应变公式宏观化的方式进行二维平面弯曲状态的理论推导，在文献[18]中已有详细推导，如图9所示，在此简述如下。

图9 连续体机械臂弯曲变形模型Fig.9 Bending deformation model of continuous manipulator

给定L,θ的二维平面下末端执行E点坐标，图中L，L1，L2为柔性臂弯曲时的各柔性杆弧长，θ为弧长角，ρ，ρ1，ρ2分别为L，L1，L2的曲率半径，E(x,y)为中间杆L的顶点坐标。

在十字架的支撑之下，L1，L2与L各段之间间距相同，由弧长公式可得

(4)

E点坐标x,y利用三角函数推导得到

(5)

由式(4)，(5)推导得到E点坐标x，y关于L，θ的方程为

(6)

其中：x，y为连续体机械臂末端在xOy平面内的坐标。

将x,y对时间求导，得到x,y方向的速度为

(7)

(8)

联立式(3)，(8)，求得连续体机械臂到达目标位置后末端振幅。

2.4 连续体机械臂末端阻尼振动模型的确立

(9)

将式(9)中的A，τ带入式(1)，得到

(10)

2.5 振动特征参数的确定

通过实验可测定式(2)中振动特征参数ωd和σ。实验中取100组参数，得到ωd与机械臂长度L、弯曲角θ的关系，如图10所示。

图10 固有频率ωd关于机械臂长度L与弯曲角度θ的曲面关系图Fig.10 Surface relation diagram of frequency ωd between elongation and angle

由图10可知，连续体机械臂在长度为500 mm、弯曲角度为90°时, 阻尼固有频率ωd最高，随着机械臂长度L的增大和弯曲角θ的降低，阻尼固有频率ωd逐渐减小。

利用Matlab软件中的Cftool模块，将图10中的实验数据进行曲面拟合，得到

0.000 119L2-0.000 218 4θL

(11)

拟合后曲面如图11所示,其多项拟合度指标如表3所示。

图11 图10中阻尼固有频率ωd拟合图片Fig.11 Fit picture of damped natural frequency

表3 阻尼固有频率拟合度Tab.3 Fitness of Damped natural frequency

实验中，同样可得到100组连续体机械臂衰减系数σ关于连续体机械臂弯曲角θ和伸长量L的关系，如图12所示。

图12 衰减系数σ关于机械臂长度L与弯曲角度θ的曲面关系Fig.12 Surface relation diagram of attenuation coefficient σ between the elongation L and angle θ

拟合后的公式为

7.415×10-6L2+1.458×10-5Lθ

(12)

拟合后曲面如图13所示，拟合度如表4所示。

图13 衰减系数σ拟合图片Fig.13 Fit picture of attenuation coefficient σ

3 阻尼振动位移模型的验证

连续体机械臂末端阻尼振动模型验证实验由放置连续体机械臂末端的激光标记点，标定棋盘纸，高速摄像机组成。高速摄像机为瑞士AOS公司生产的S-MIZE HD v2，采样频率为200 Hz，采样分辨率为1 280*720dpi。由高速摄像机拍摄连续体机械臂在固定位姿下振动情况，通过采集激光标记点振动位移变化，通过长宽均为20 mm黑白相间棋盘纸标定,纸将像素单位转化为长度单位，经高速相机标定测量，1pixels像素等于0.34 mm长度。采集下的标记点图像通过瑞士AOS公司开发的图像处理软件处理振动位移曲线。验证实验装置如图14所示。连续体机械臂末端阻尼振动模型验证实验由高速摄像机拍摄曲线与拟合模型(10)结果相对比。角速度由Mpu6050加速度传感器实际测得。取识别样本之外的4组伸长量及弯曲角度参数进行验证，实验参数如表5所示。

表4 衰减系数拟合度Tab.4 Fitness of Attenuation coefficient

图14 连续体机械臂振动实验测量平台Fig.14 Experimental platform for vibration of continuous manipulator

表5 验证实验组参数Tab.5 Verify the number of experimental groups

将连续体机械臂末端拟合公式与实际高速摄像机拍摄图像对比，第1组实验结果如表6所示。图15为全部4组实验的理论模型与实验对比。

表6 连续体机械臂理论数值与实际试验计算数据Tab.6 Theoretical value and actual test data of continuum manipulator

图15中，实线为连续体机械臂末端振动模型(7)随时间变化得出曲线，虚线为高速摄像机实际拍摄曲线。由于阻尼固有频率ωd、衰减系数σ均由式(8)和式(9)得到，故实际测量值与理论计算数值会有误差。第2～第4组验证实验结果如表7所示，所有数据验证结果实际测量值与理论计算值的误差小于10%。在时间与位移关系方面，由图15可知，由于误差的累积效应，误差会随着时间的增长而逐渐增大，机械臂振动抑制通常在前两三个周期内完成。因此，本研究所提出的模型完全可作为连续体机械臂抑振时的模型来使用。

图15 连续体机械臂末端振动曲线拟合图像Fig.15 Fitting image of continuous manipulator manipulated end point vibration curve

表7 连续体机械臂验证实验对照Tab.7 Verification of test accuracy by flexible continuous manipulator

4 结 论

1) 本研究根据连续体机械臂动力学的复杂特性，搭建了可变长度的连续体机械臂的实验台。发现随机械臂长度及弯曲角度的变化，其各阶振动模态有规律地连续变化，且具有相同的模式。其二阶及以上的振动模态会在一阶模态振动的第2,3个周期内衰减为零。

2) 建立连续体机械臂随长度及弯曲角度变化的数学模型。基于加速度传感器，通过振动激励和参数识别的方式，定量拟合出了在规定范围内任意长度与任意弯曲角度下、连续体机械臂的阻尼固有频率与衰减系数关于伸长量与弯曲角度的函数关系式，解决了此类多杆连续体机构无法通过公式推导计算得出振动相关量的难点。

3) 基于加速度传感器测量出的连续体机械臂末端角速度，拟合出了在规定范围位姿下，连续体机械臂末端在到达目标位置后的振动方程，并通过高速摄像机拍摄连续体机械臂振动与振动函数模型相对比。实际测试振动参数与理论振动参数较为符合，误差小于10%。本研究结果为连续体机械臂的主动振动抑制奠定了基础。

[1] 王雯静，余跃庆，王华伟.柔顺机构国内外研究现状分析[J]. 机械设计, 2007, 24(6)：1-4.

Wang Wenjing, Yu Yueqing, Wang Huawei. An analysis of the current situation sophisticated of current status of the research[J]. Journal of Machine Design, 2007, 24(6)：1-4. (in Chinese)

[2] 徐先洋, 应小刚, 邵世明, 等. 平面柔顺机构力学特性的研究进展[J]. 机械制造, 2016, 54(6): 89-92.

Xu Xianyang, Ying Xiaogang, Shao Shiming, et al. Research progress on mechanical properties of planar softening mechanism[J]. Machinery, 2016, 54(6): 89-92. (in Chinese)

[3] 侯文峰. 考虑温度效应的柔性和柔顺机构弹性动力学研究[D]. 广州：华南理工大学, 2009.

[4] 邱冬. 基于连续体机构的肩部外骨骼机器人的设计、建模及试验验证[D]. 上海：上海交通大学, 2013.

[5] 王斌锐, 方水光, 金英连. 综合关节和杆件柔性的机械臂刚柔耦合建模与仿真[J]. 农业机械学报, 2012, 43(2): 211-215.

Wang Binyue, Fang Shuiguang, Jin Yinglian. Dynamics and simulation of rigid-flexible coupling robot arm with flexible joint and link[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(2): 211-215. (in Chinese)

[6] 屠立, 周丕宣, 张树有. 柔性机械手机械结构与自适应控制全局优化设计[J]. 农业机械学报, 2008, 39(8): 128-134.

Tu Li, Zhou Pixuan, Zhang Shuyou. Global optimization design of flexible manipulator structure and adaptive control[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(8): 128-134. (in Chinese)

[7] 唐红梅. 连续体型震后救援机器人运动学研究[D]. 天津：河北工业大学, 2012.

[8] 赵志刚, 陈志刚. 柔性气动连续体机器人关节结构设计与运动学分析[J]. 机械科学与技术, 2015, 34(2): 184-187.

Zhao Zhigang, Chen Zhigang. Mechanism design and kinematics analysis of pneumatic soft continuum robot joint[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(2):184-187. (in Chinese)

[9] 李亚锋, 赵江海, 章小建, 等. 线驱动混合关节机器人构型与运动控制分析研究[J]. 制造业自动化, 2016, 38(8): 36-40.

Li Yafeng, Zhao Jianghai, Zhang Xiaojian, et al. Research of the mechanism configuration and motion control for the cable-driven hybrid joint robot[J]. Manufacturing Automation, 2016, 38(8):36-40. (in Chinese)

[10] 徐秀秀, 郭毓, 余臻,等. 基于机器视觉的柔性臂振动测量研究[J]. 华中科技大学学报: 自然科学版, 2013, 41(S1): 129-132.

Xu Xiuxiu, Guo Yu, Yu Zhen, et al. Vibration measurement of flexible beam based on machine vision[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 2013, 41(S1):129-132. (in Chinese)

[11] 刘兴占, 张令波, 孙富春. 柔性双连杆机械臂末端振动测量的研究[J]. 光学技术, 2000, 26(3):241-243.

Liu Xingzhan, Zhang Lingbo, Sun Fuchun. Study of measuring vibration on extremity of the flexibility arm[J]. Optical Technique, 2000, 26(3):241-243. (in Chinese)

[12] 邱志成, 张祥通. 基于视觉的柔性结构振动测量及其控制[J]. 振动、测试与诊断, 2012, 32(1): 11-16.

Qiu Zhicheng, Zhang Xiangtong. Visual-based flexible structural vibration measurement and control[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 11-16. (in Chinese)

[13] Mahmood I A, Moheimani S O R, Bhikkaji B. Precise tip positioning of a flexible manipulator using resonant control[J]. IEEE/ASME Transactions on Mechatronics, 2008, 13(2):180-186.

[14] Wang Hesheng, Chen Weidong, Xu Lifei, et al. Vision-based online vibration estimation of the in-vessel inspection flexible robot with short-time Fourier transformation[J]. Fusion Engineering & Design, 2015, 98-99:1683-1687.

[15] 王辉. 压电柔性臂冲击振动的瞬态响应及其抑制研究[D]. 上海：华东交通大学, 2013.

[16] 张庆. 组合柔性机械臂动力学特性与振动抑制性能的研究[D]. 南京：南京理工大学, 2010.

[17] Goldman R E, Bajo A, Simaan N. Compliant motion control for multisegment continuum robots with actuation force sensing[J]. IEEE Transactions on Robotics, 2014, 30(30): 890-902.

[18] Gao Guohua, Liu Yue, Wang Hao, et al. Workspace calculating and kinematic modeling of a flexible continuum manipulator constructed by steel-wires[J]. Industrial Robot, 2015, 42(6): 565-571.