环形梯度多胞结构的多工况耐撞性研究
2018-03-06林继铭赖雄鸣
张 勇 曾 意 徐 翔 林继铭 赖雄鸣
华侨大学机电及自动化学院,厦门,361021
0 引言
圆形薄壁结构因具有质量小、吸能高等优点而被广泛应用于汽车、高速列车的吸能结构。早期研究主要集中于圆形单管结构,ALEXANDER[1]提出了一种理论模型来预测圆管在轴向冲击下的平均碰撞力;WIERZBICKI等[2-3]对圆管的轴向冲击进行了实验研究和理论预测;KARAGIOZOVA等[4]对圆形薄壁管的动态轴向吸能进行了研究,发现圆管的厚度、细长比对能量吸收有重要影响;LUO等[5]研究了不同材料对金属圆管耐撞性能的影响;NIA等[6]、XIANG等[7]采用实验和仿真方法对圆管、四边形以及六边形等薄壁管开展轴向碰撞研究,发现圆管比同质量的其他多边形管具有更好的能量吸收能力。然而,单胞圆管受到冲击时常存在变形不稳定的缺陷,因此,具有更好轴向刚度及吸能特性[8]的多胞结构逐渐引起了人们的关注。CHEN等[9]提出了一种理论公式来预测圆形多胞薄壁管的平均碰撞力;TABACU[10]通过理论和仿真方法对圆形多胞坍塌模式进行了研究;TANG等[11]采用数值方法对不同截面的多胞圆柱管进行研究,发现圆形多胞管比方形多胞管具有更好的能量吸收能力。然而,上述研究仍集中在具有均匀材料特性的圆形单胞与多胞管,而均匀结构在冲击过程中不可避免地存在峰值碰撞力较大的缺陷,因此,具有材料特性梯度变化的复合结构逐渐引起了研究人员的兴趣。CUI等[12]提出了一种梯度泡沫材料,发现梯度泡沫材料比均匀泡沫材料具有更好的能量吸收能力;SUN等[13]通过理论研究和数值仿真发现,梯度泡沫填充管的梯度指数对其吸能特性有重要的影响;YIN等[14]通过理论和数值研究发现,梯度管的截面构型和材料都对其能量吸收能力有很大的影响。然而,圆形梯度多胞结构在多角度冲击工况下的耐撞性研究仍鲜见报道。本文提出了一种新颖的双层环形梯度多胞结构,并探测其在轴向与斜向多冲击工况下的耐撞性。
1 环形梯度多胞结构
1.1 环形梯度多胞管的耐撞性模型
图1a为环形多胞结构在不同角度冲击下的冲击示意图,α为冲击角度,表示刚性墙冲击平面法向与多胞管顶端平面法向之间的夹角,α在0°~30°之间变化,冲击速度v=10 m/s,刚性墙质量为500 kg,多胞管固定在底部支撑板上。图1b所示为多胞管的横截面形状,环形多胞结构的外管与内管直径分别为60 mm和30 mm,长度L=200 mm。
图1c和图1d分别为梯度结构与均匀结构在A-A位置的剖视图。由图1c可知,环形多胞管的梯度特性体现为壁厚沿轴向规律变化,包含两种厚度分布形式:一种是从冲击端到支撑端厚度由小到大分布的升梯度结构;另一种是从结构的冲击端到支撑端厚度由大到小分布的降梯度结构,升梯度结构的厚度分布规律为
tf(x)=tmin+(tmax-tmin)(x/L)n
(1)
降梯度结构的厚度分布规律为
tf(x)=tmax-(tmax-tmin)(x/L)n
(2)
其中,L为多胞管的长度;x为任意截面距离顶端的距离(图1c);tmin=0.8 mm和tmax=1.5 mm分别为壁厚分布的最小值与最大值;n为梯度指数,其取值分别为0.2,0.4,0.6,0.8,1,3,5,7,9,10。
此外,已有研究表明,升梯度结构比降梯度结构具有更好的吸能特性[15],因此,本文重点开展升梯度环形多胞结构(式(1))的耐撞性研究。

(a)环形多胞管的冲击示意图 (b)横截面的形状

(c)升梯度管剖面图(d)均匀结构剖面图图1 环形多胞管的几何模型Fig.1 The geometric model of annular multi-cell tubes
1.2 环形梯度多胞管的数值模型
为了建立厚度呈指数分布的环形梯度结构的数值模型,本文将梯度结构离散为40层[15],使每一层具有均匀厚度。图2所示为梯度结构的厚度指数分布曲线。同时,在LS-DYNA软件中建立环形梯度多胞管的有限元模型,如图3所示。多胞管和支撑板都采用1 mm×1 mm的BT四节点壳单元进行离散。
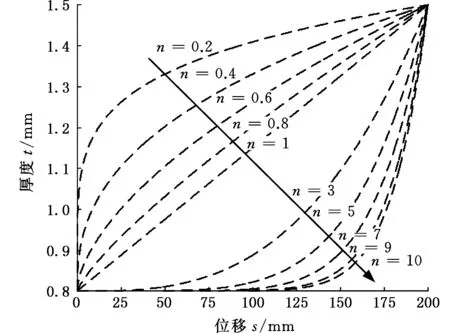
图2 递增模式下不同梯度指数的壁厚分布Fig.2 The wall thickness distribution of differentgradient index in ascending grading pattern

(a)梯度多胞管 (b)均匀多胞管图3 环形多胞结构的有限元模型Fig.3 Finite element models of annular multi-cell tubes
环形多胞管和刚性墙之间采用自动点面接触,为了模拟结构在压缩过程中变形引起的自接触,对环形梯度多胞管自身采用自动单面接触,且静态与动态摩擦因数均取0.3。此外,环形梯度多胞结构的材料为铝合金AA6060,其密度ρ=2 700 kg/m3,弹性模量E=68.2 GPa,泊松比υ=0.3。工程应力-应变曲线如图4所示,由于铝合金材料对应变率不敏感,故建模时不考虑应变率对材料参数的影响[16]。

图4 AA6060的工程应力-应变曲线Fig.4 Stress-strain curve for AA6060
1.3 耐撞性指标
动态冲击过程中,比吸能 (specific energy absorption)ESEA和峰值力(peak crushing force)FP是两个主要的耐撞性评价指标。其中,ESEA表征单位质量的能量吸收率,其值越大,代表结构具有越高的能量吸收能力,可表示为
ESEA=EA/M
(3)
其中,M表示薄壁构件的总质量,EA(energy absorption)表示总能量吸收,即
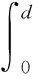
(4)
EA也可用冲击过程中的平均碰撞力Pm来表示,即
Pm=EA/d
(5)
其中,d为碰撞吸能过程中的有效压缩位移,取管总长度的70%;x为压缩距离;F(x)为瞬时碰撞冲击力。
FP为F(x)的最大值,较大的FP会引起较大的减速度,从而导致对乘员的严重伤害,因此,冲击过程中需确保FP在人体可承受的范围内。
1.4 环形多胞结构的理论模型
首先推导了环形多胞结构(图5a)的平均碰撞力理论模型,并以此来验证本文环形多胞结构有限元模型的可靠性。
薄壁结构的平均碰撞力Pm由能量守恒定律可表示为[17]
Pm=(Eb+Em)/(2kH)
(6)
式中,H为结构压缩折叠的波长;k为有效位移与总长度的比值;Eb为弯曲耗能;Em为全部的膜片形变能。
传统单胞圆管的弯曲耗能[17]
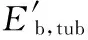
(7)
式中,M0为充分变形的塑性弯矩[18];R0为单胞圆管的半径。
基于式(7),针对本文所提的双层环形双壁结构,其弯曲耗能
Eb,tub=4π2M0(R+r)
(8)
式中,R为外管的半径;r为内管的半径。
同时,针对多胞管内薄壁嵌入片(inserts,见图5a)的弯曲能[18]
(9)
式中,θ为每个凸缘的铰接线的旋转角度(图5b);Li为环形圆管内嵌入片横截面的总长度。
考虑嵌入片在变形中皆被充分压缩(图5c),因此,嵌入片的弯曲能可简化为
Eb,ins=2πM0Li
(10)

(a)环形多胞管的截面图 (b)凸缘折叠示意图(c)凸缘充分压缩示意图图5 环形多胞管变形图Fig.5 Deformation figure of annular multi-cell tube
环形多胞结构的总弯曲耗能
Eb=Eb,tube+Eb,ins
(11)
此外,圆形单胞结构的膜片形变能[17]

(12)
基于式(12),由于环形多胞结构由两个圆形单胞管组成,其膜片形变能
Em,tub=4πN0H2
(13)
式中,N0为单位长度的塑性膜片力。
环形多胞结构中嵌入结构的膜片形变能则可以通过T形连接区域(T-shape,见图5a)来表示。其中,每个T形连接消耗的膜片形变能
ET=N0H2
(14)
因此,本文所提的环形多胞结构(图5b)的总膜片形变能
Em=Em,tub+NTCEm,T
(15)
式中,NTC为类T形连接的数目。
整理以上公式并代入式(6),得
(16)
(17)
此外,为了减小T形连接引起的不均匀性影响,引入补偿系数λ[17]:
λ=sin(2π/NTC)
(18)
最终得到的环形多胞结构的平均碰撞力的理论模型为
(19)
式中,σ0为材料的流动应力;LC为截面结构的总长度;DC为动态冲击惯性力影响系数[19],其取值范围为1.3~1.6。
基于式(19)获得的Pm的理论模型,管的厚度t=1 mm,代入式(19),求得其理论平均碰撞力Pm=19.51 kN。图6为环形多胞结构的有限元计算曲线与本文理论模型的Pm的对比图,可以发现有限元计算分析得到的平均碰撞力为18.96 kN,与理论模型的计算值相差不足5%,从而表明本文使用的有限元模型具有准确性。
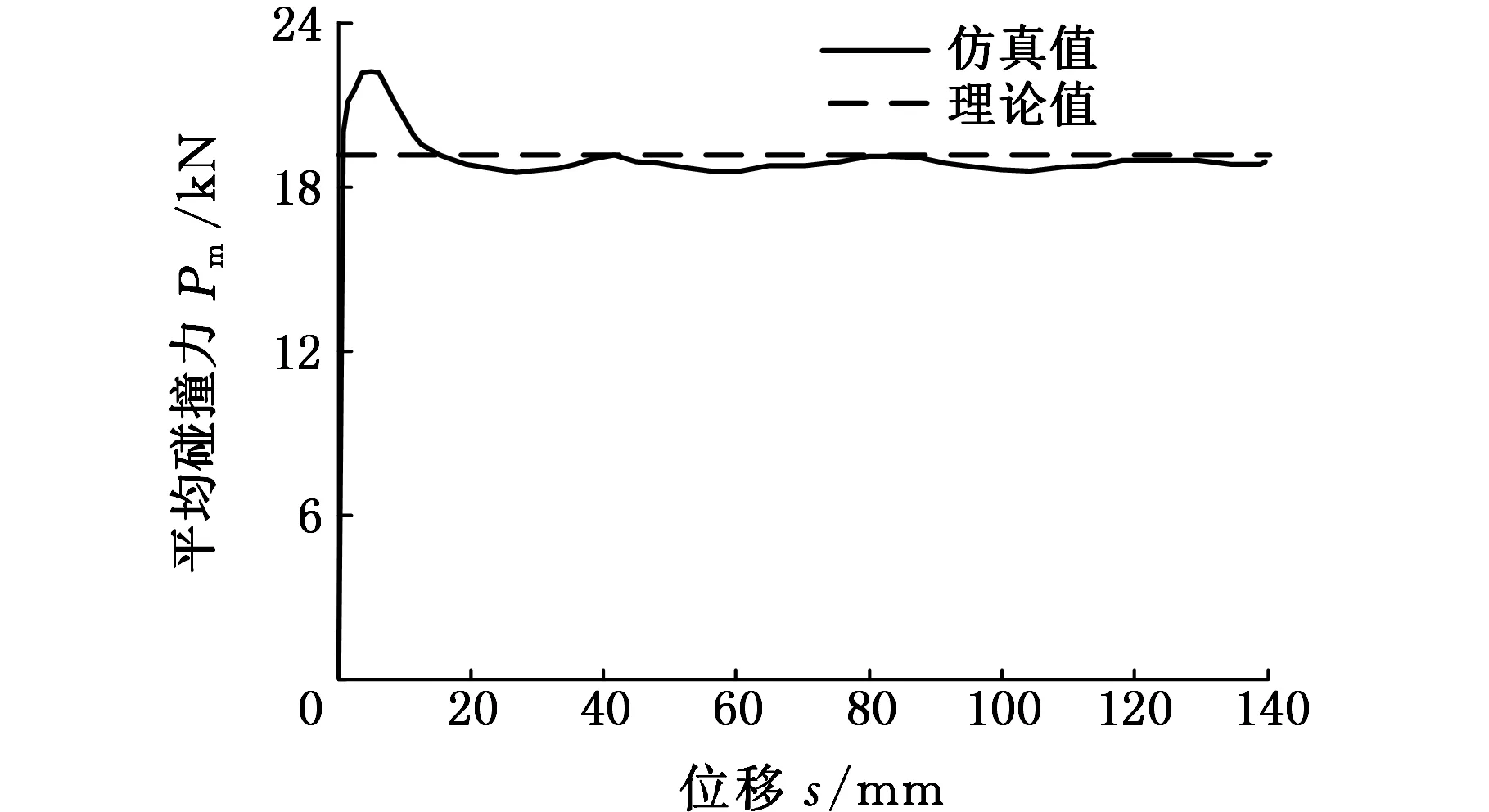
图6 理论预测与数值计算对比Fig.6 Comparing of theoretical and computing value
本文也选取了具有更多胞元(图7)的双层环形多胞管来进一步验证本文理论模型的可行性。图7中不同多胞管的各项参数与图5a中相同,其有限元计算值与理论模型计算值见表1。由表1可知,计算值和理论值的相对误差均不足5%,从而进一步验证了本文理论模型的可行性,也进一步验证了本文有限元模型的可靠性。
(a)6胞管 (b)8胞管 (c)10胞管图7 三种环形多胞管Fig.7 Three different annular multi-cell tubes
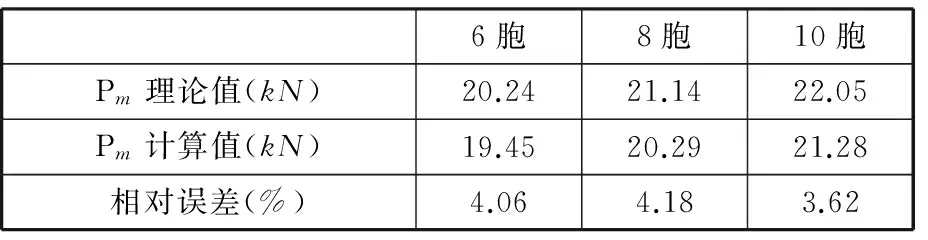
6胞8胞10胞Pm理论值(kN)20.2421.1422.05Pm计算值(kN)19.4520.2921.28相对误差(%)4.064.183.62
1.5 环形多胞结构数值模型的实验验证
为了验证本文理论模型及有限元模型的正确性与普遍适用性,本文设计了图8a所示的实验试件。其中,环形多胞管的长度为100 mm,外管和内管的直径分别为50 mm和35 mm,壁厚为0.8 mm。环形多胞管加工采用的材料为铝合金AA6061-T5,其弹性模量E=68 GPa,泊松比υ=0.3,屈服应力σy=230 MPa,极限应力σu=290 MPa,并开展5 mm/min的准静态压缩实验。图8b~图8d分别为试件压缩10 mm、30 mm和50 mm三种不同压缩位移下实验和相应的有限元模型的压缩变形图。可知,在相同的压缩位移内,实验和仿真得到的折叠数量相同,并且实验试件的变形模式与有限元仿真的变形模式也较为一致。图9进一步给出了数值分析和实验

(a)实验样品(b)压缩位移10 mm

(c)压缩位移30 mm(d)压缩位移50 mm图8 环形多胞管的实验与仿真对比Fig.8 Comparison of simulation and test for annular multi-cell tube
所获得的压缩力-位移曲线。可以看出,数值仿真和实验的压缩力-位移曲线整体趋势较为吻合,因此,通过实验与仿真在各压缩阶段变形模式及力-位移曲线地对比,较好地验证了本文有限元模型的可靠性。并且,图9也给出了预测模型(式(19))得到的平均碰撞力曲线,理论预测、实验和仿真得到的平均碰撞力分别为28.34 kN、28.61 kN和27.56 kN,各值相差均不足5%,从而进一步验证了本文理论模型的可行性。
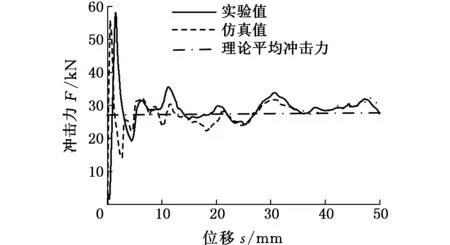
图9 力-位移曲线Fig.9 Force-displacement curves
2 环形多胞结构的多工况耐撞性研究
本文选取六种工况(α=0°,5°,10°,15°,20°,30°)来对比梯度结构与均匀结构的耐撞性,并且,保持每种工况下各结构的质量一致,不同梯度指数梯度结构对应同质量均匀结构的厚度见表2。

表2 不同梯度指数的梯度结构所对应均匀结构的壁厚
2.1 比吸能对比分析
图10所示为梯度多胞结构和对应的均匀结构在不同的碰撞角度下的ESEA。两种结构的ESEA随着梯度指数的增大而减小,表明梯度指数对多胞结构的能量吸收能力有显著影响,主要原因是梯度指数的变化会引起多胞管壁厚分布的变化,不同梯度结构在同一位置的厚度随梯度指数的增大而减小(图2);而对于均匀结构,梯度指数越大,其同质量均匀结构的壁厚越小(表2),材料使用率也相应减小,从而导致其ESEA逐渐减小。
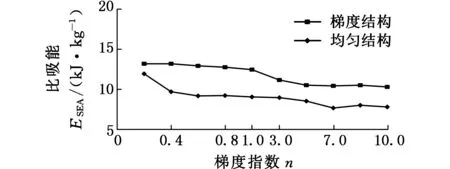
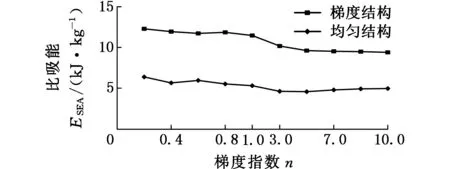
当冲击角度α≤5°时,两种结构的ESEA较为接近,表明在小角度冲击下,梯度多胞结构的能量吸收能力无明显优势;当α≥10°时,梯度结构的能量吸收能力则表现出明显的优势;当α=10°时,梯度结构(n=0.6) 的ESEA比均匀结构增大最大达40.86%(图10c);而α=15°时,梯度结构的ESEA(n=0.4)比均匀结构增大最大可达113.49%(图10d);当α增大到20°时,梯度结构(n=0.6)的ESEA比均匀结构增加的最大幅度为170.56% (图10e)。

(a)α=0°
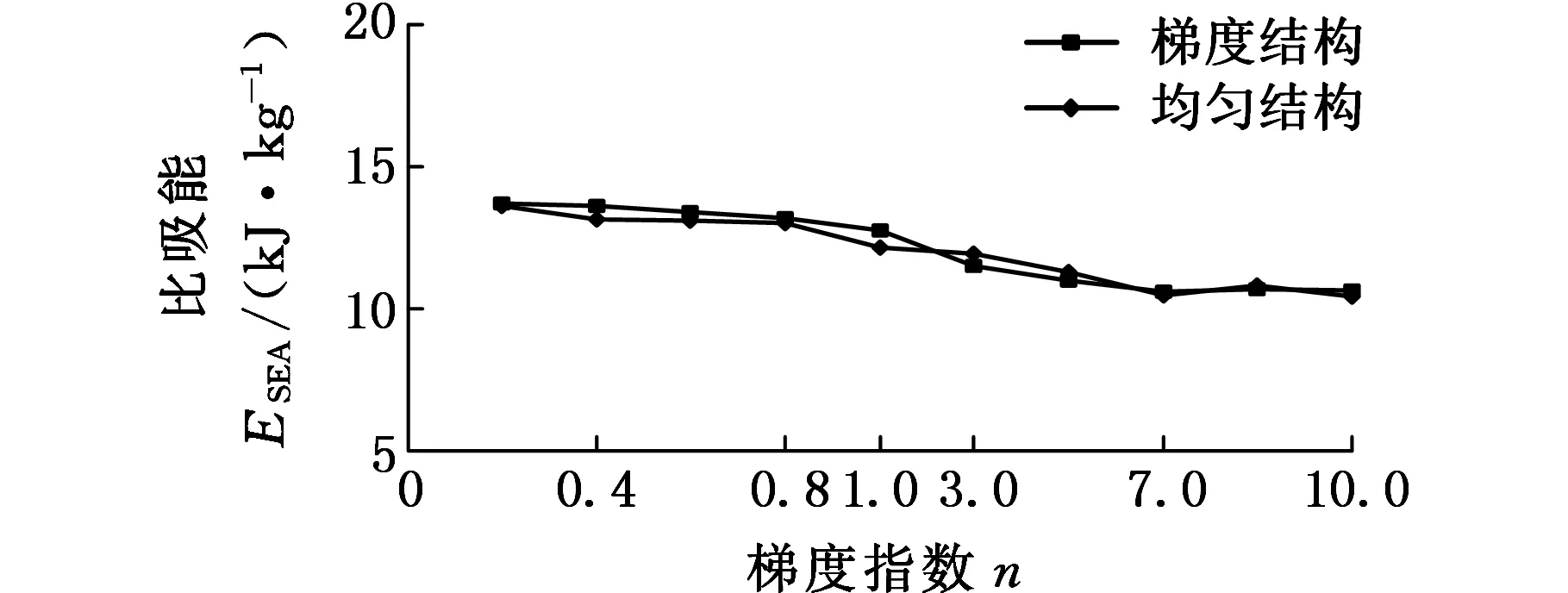
(b)α=5°
(c)α=10°
(d)α=15°

(e)α=20°

(f)α=30°图10 不同碰撞角度下比吸能随梯度指数的变化Fig.10 Change of ESEA along with gradient index under different collision angles
图11所示为梯度结构(n=0.6)与均匀结构在α=20°的大角度冲击下的变形模式,由图可知,均匀结构在压缩初期即在底部发生了全局屈曲失稳变形,使得其吸能特性大大降低,主要原因是均匀结构在受到大角度斜向冲击时,环形结构受到的弯矩在固定端最大,使得底端率先出现塑性变形,导致底部失稳发生全局弯曲。然而,梯度结构由于厚度呈指数分布(图2),顶部冲击端的厚度小、刚度小,而底部支撑端的厚度大、刚度大,使其刚度从顶端到底端逐级变化。当受到冲击时,刚度小的顶部首先发生塑性变形,底部刚度大因而不容易弯曲失稳,从而能较好地抵抗斜向冲击载荷,在较大角度斜向冲击下仍能保持较好的逐级折叠吸能性。

(a)均匀结构

(b)梯度结构图11 两种结构在20°冲击角度下的变形模式Fig.11 Deformation pattern of two structures under α=20°
当α增大到30°时,梯度结构的ESEA相比均匀结构增大的幅度并没有继续增大(图10f),这是因为α增大到30°时,梯度结构在压缩一段距离后也会发生全局失稳(图12),从而使得其能量吸收能力降低,但其ESEA仍大大高于均匀结构的ESEA(图10f)。
2.2 峰值碰撞力对比分析
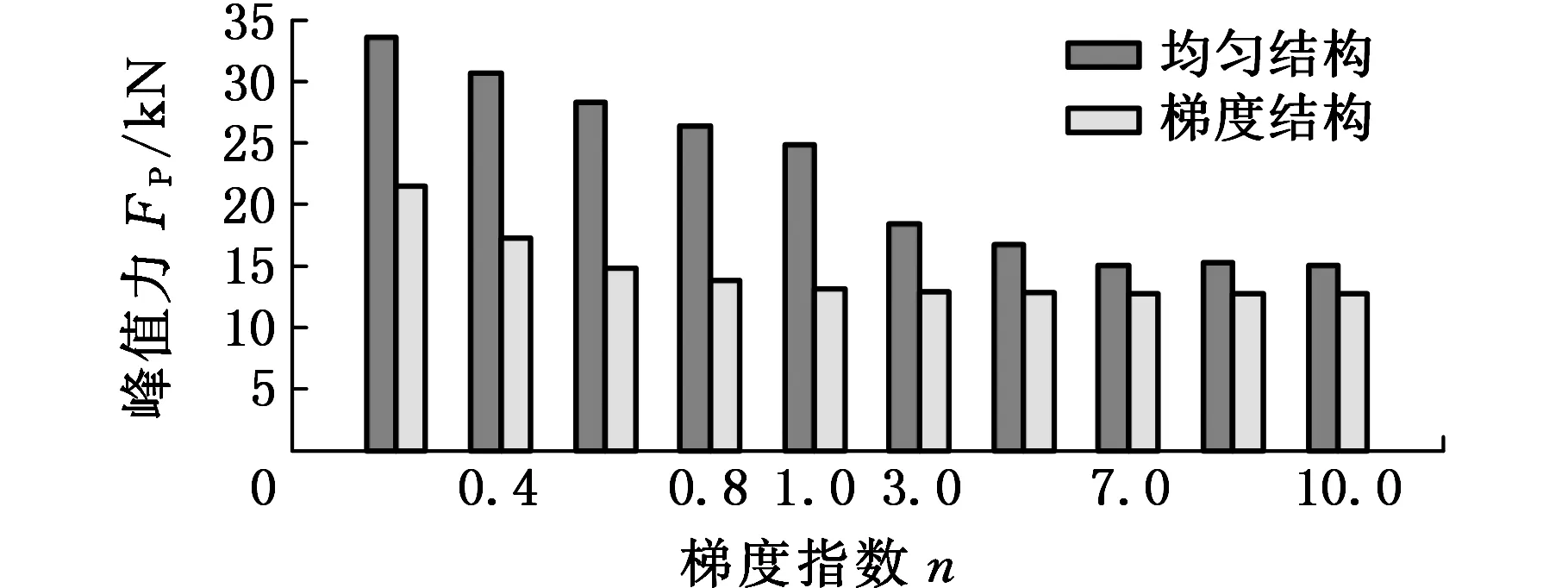
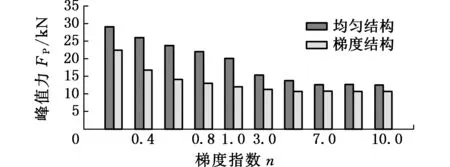
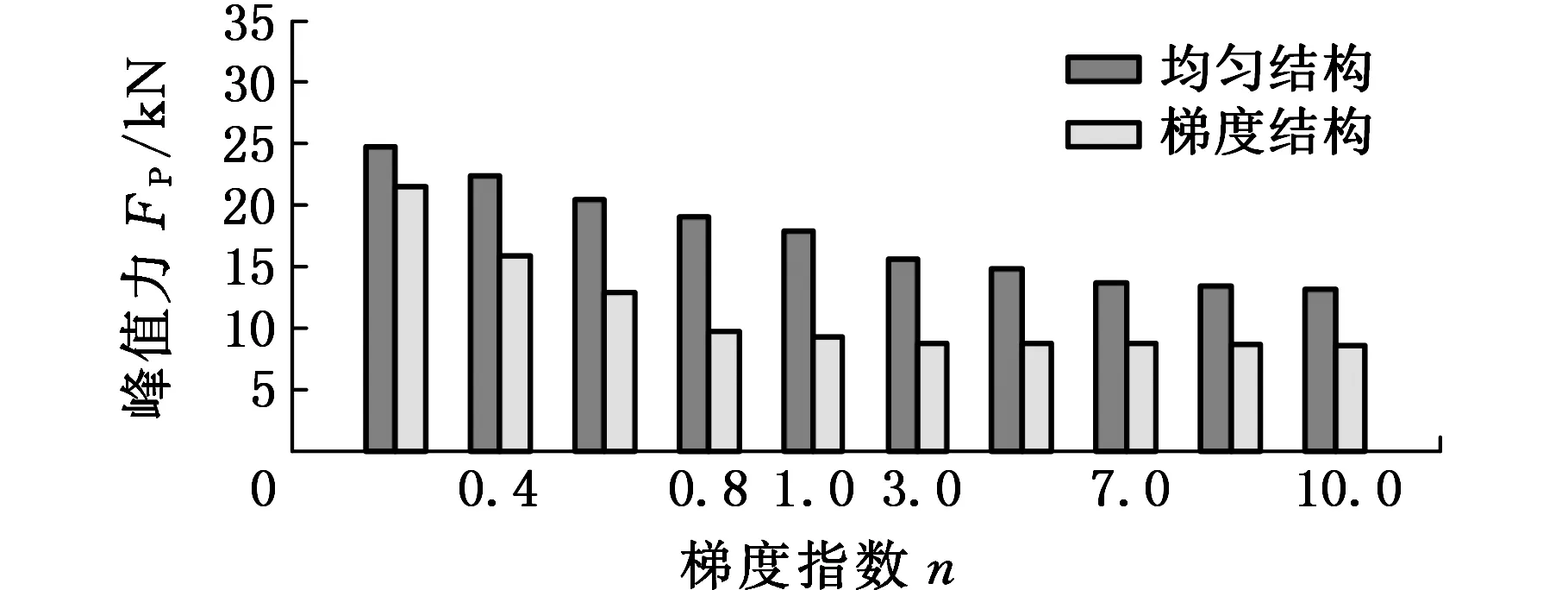
图13所示为两种结构在不同冲击工况下的FP。FP均随梯度指数n的增大而减小,而当n>1后,FP形成逐渐收敛的趋势,主要原因是当n>1时,均匀结构的厚度分布差异越来越小(表2),而梯度结构的厚度分布也较为接近,因此,它们各自的FP逐渐收敛,从而表明n对结构的轴向刚度有显著影响,n越大,越有利于获得较小的FP。
在相同的梯度指数下,两种结构的FP随着α的增大都会减小,主要原因是α的增大使得结构的受力面积有所增大,单位作用面积受力减小。另外,梯度结构的FP皆小于对应的均匀结构的FP,表3给出了不同α下梯度结构的FP相比均匀结构的减小率,由表3可知,不同的α作用下,梯度结构的FP比均匀结构皆可减小30%以上,且在α=20°时,FP减小了51.48%,表明梯度材料特性使结构具有更好的力学分布特性。

(a)均匀结构
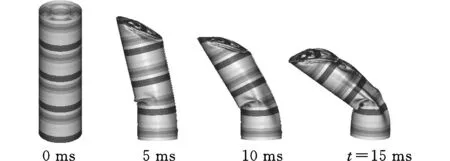
(b)梯度结构图12 两种结构在30°冲击角度下的变形模式(n=0.6)Fig.12 Deformation pattern of two structures under α=30°(n=0.6)

表3 梯度结构的FP比均匀结构的减小率
2.3 梯度厚度区间对耐撞性的影响
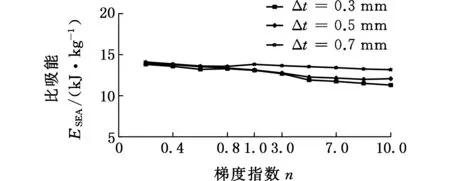
为了进一步探索材料的梯度特性,本文研究了不同梯度厚度区间对其耐撞性的影响。选取梯度结构的最小厚度值tmin=0.8 mm,1.0 mm,1.2 mm;而tmax则仍然保持在1.5 mm,从而形成具有三种不同厚度区间Δt=tmax-tmin(0.3 mm,0.5 mm,0.7 mm)的梯度结构。图14所示为三种厚度区间的梯度结构在不同冲击工况下的ESEA。在不同的冲击角度下,Δt=0.7 mm对应的梯度结构的ESEA均最大,而Δt=0.3 mm对应的梯度结构则具有最小的ESEA,表明适当扩大梯度结构的厚度区间能改善梯度结构的吸能性。
图15所示为三种厚度区间在不同冲击工况下的FP。由图15可知,三种厚度区间对应梯度结构的FP都会随着梯度指数的增大而呈现减小的趋势。并且,在不同的碰撞角度下,Δt=0.7 mm所对应的梯度结构的FP均最小,而Δt=0.3 mm所对应的梯度结构的FP均最大,表明适当扩大梯度结构的厚度区间能较好地降低其峰值力特性。由此可知,厚度区间对梯度结构的耐撞性有重要的影响。

(a)α=0°

(b)α=5°
(c)α=10°
(d)α=15°
(e)α=20°
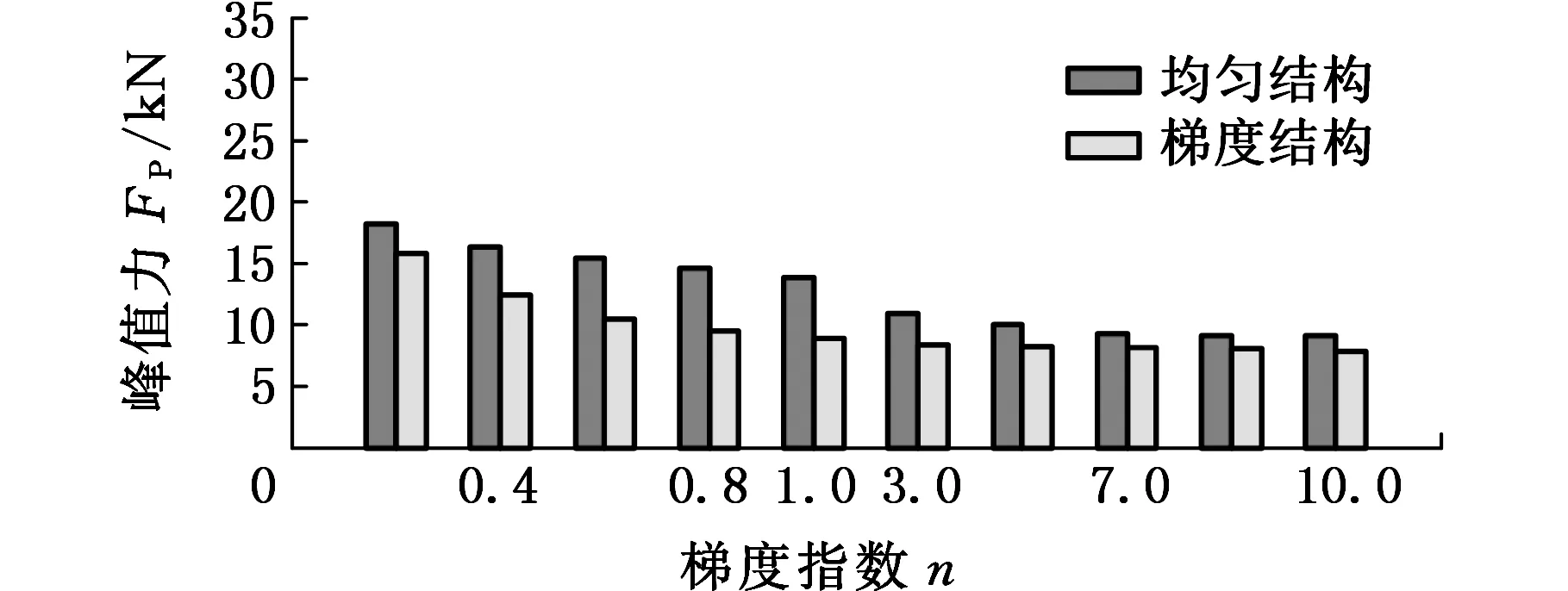
(f)α=30°图13 两种结构在不同梯度指数和角度下的峰值碰撞力Fig.13 Peak impact force of two structures under different gradient index and angles
(a)α=0°

(b)α=10°
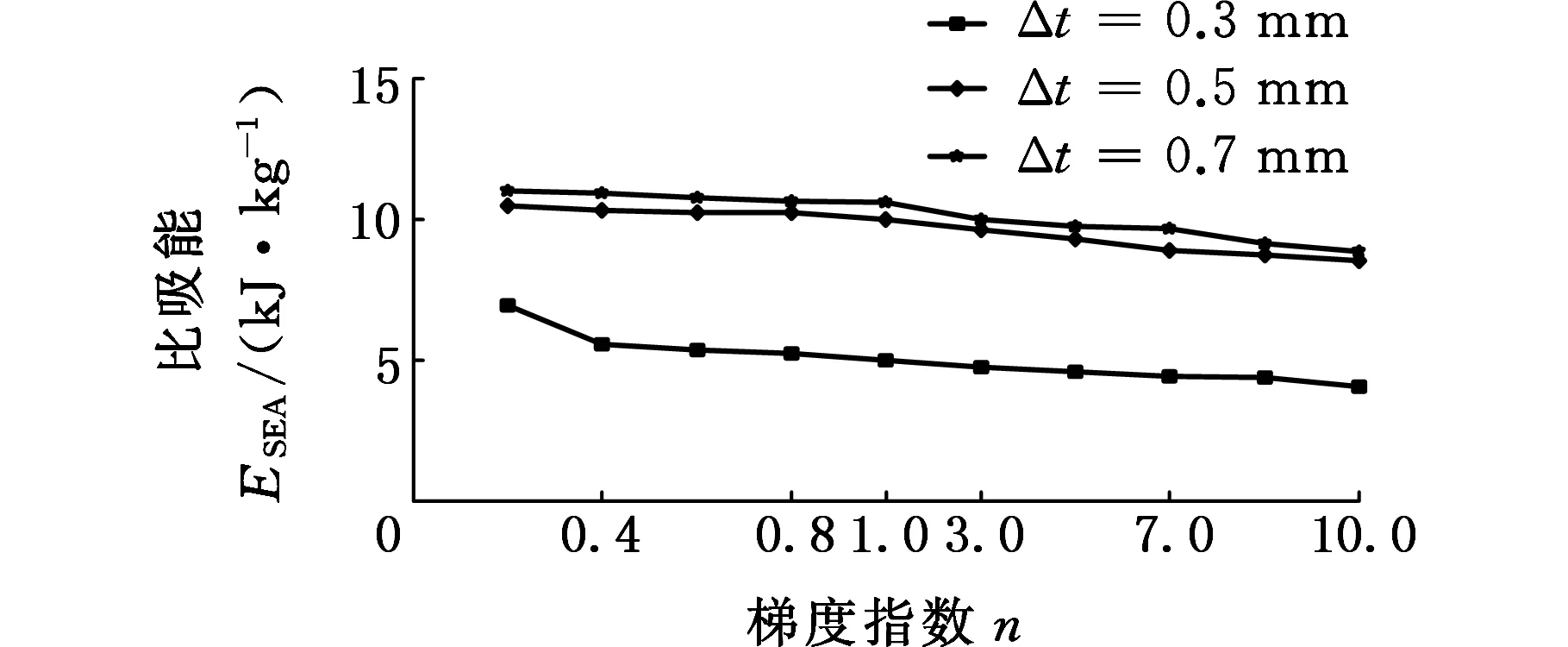
(c)α=20°

(d)α=30°图14 三种不同厚度区间的梯度结构在不同梯度指数和冲击角度下的比吸能Fig.14 ESEA of three gradient structures with different thickness ranges under different gradient index and impact angles
3 结论
(1)本文推导的环形多胞结构的平均碰撞力理论模型能较好地表征环形结构的力特性,并能较好地验证本文环形多胞结构的数值模型的可靠性。
(2)在轴向和小角度碰撞下,两种结构的能量吸收能力相差不大,但随着碰撞角度的增大,梯度结构的能量吸收明显高于均匀结构的能量吸收,表明梯度结构在斜向碰撞时具有更好的能量吸能特性。
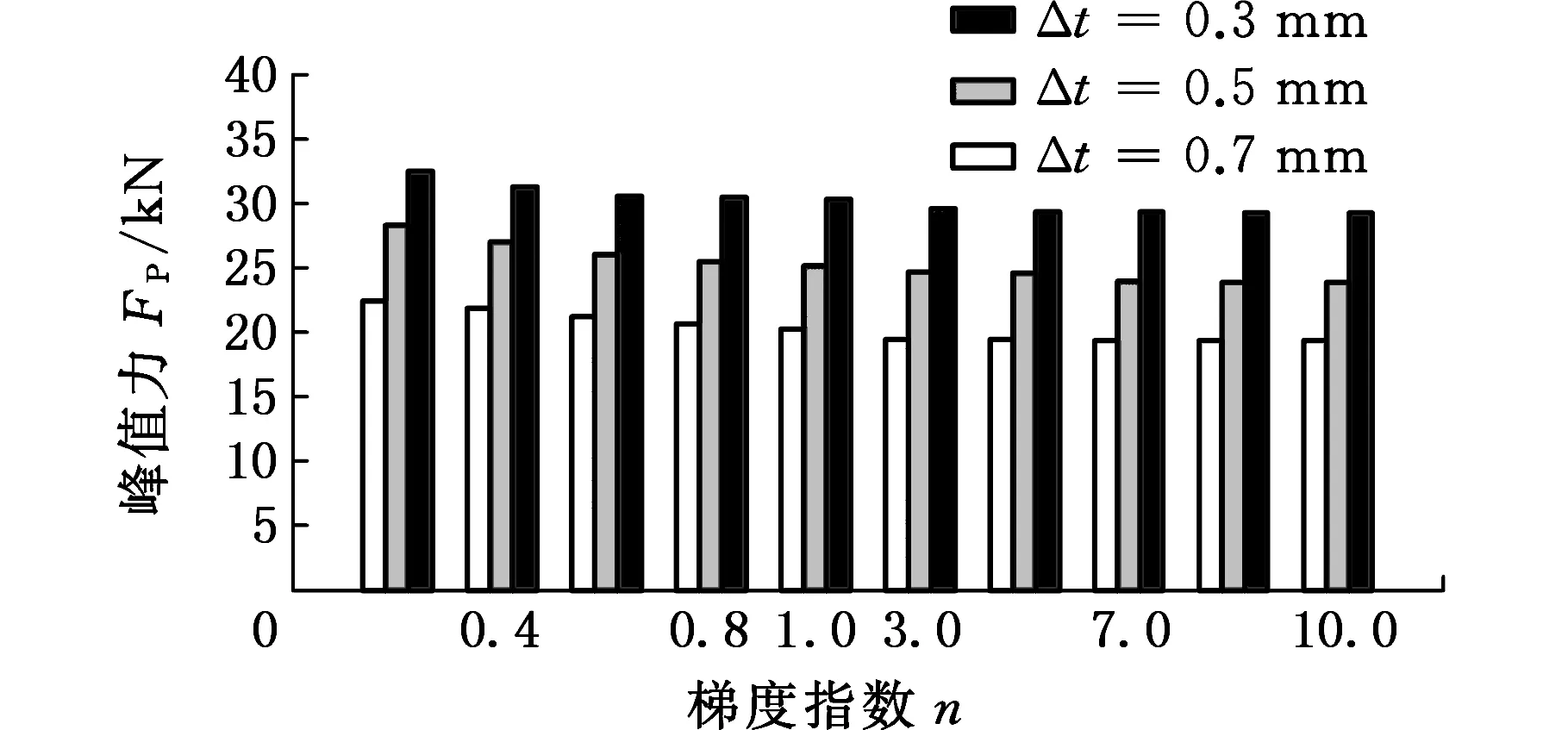
(a)α=0°
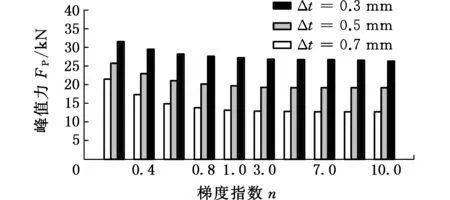
(b)α=10°

(c)α=20°
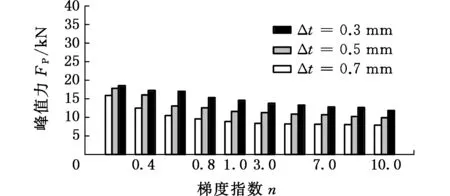
(d)α=30°图15 三种不同厚度区间的梯度结构在不同梯度指数和冲击角度下的FPFig.15 FP of three gradient structures with different thickness ranges under different gradient index and impact angles
(3)梯度指数对结构的轴向刚度具有重要影响,随着梯度指数的增大,两种结构的峰值力、能量吸收值都会减小,材料的梯度特性使结构具有更好的力学特性。
(4)梯度结构的厚度区间对结构的耐撞性有显著影响,适当扩大厚度区间能较好地改善梯度结构的耐撞性能。
[1] ALEXANDER J M. An Approximate Analysis of the Collapse of Thin Cylindrical Shells under Axial Loading [J]. Mech. Appl. Math., 1960,13(1):10-15.
[2] WIERZBICKI T, ABRAMOWICZ W. On the Crushing Mechanics of Thin-walled Structures [J]. Appl. Mech. Trans. ASME, 1983, 50(4a):727-734.
[3] ABRAMOWICZ W, WIERZBICKI T. Axial Crushing of Multi-corner Sheet Metal Columns [J]. Appl Mech. Trans. ASME, 1989, 56(1):113-120.
[4] KARAGIOZOVA D, JONES N. Dynamic Effects on Buckling and Energy Absorption of Cylindrical Shells under Axial Impact [J]. Thin-Walled Structures, 2001, 39(7):583-610.
[5] LUO Xin, XU Jinyu, ZHU Jingsai. A New Method to Investigate the Energy Absorption Characteristics of Thin-walled Metal Circular Tube Using Finite Element Analysis [J]. Thin-walled Structures, 2015, 95:24-30.
[6] NIA A A, HAMEDANI J H. Comparative Analysis of Energy Absorption and Deformations of Thin Walled Tubes with Various Section Geometries [J]. Thin-walled Structures, 2010, 48(12): 946-954.
[7] XIANG Yanfei, YU Tongxi, YANG Liming. Comparative Analysis of Energy Absorption Capacity of Polygonal Tubes, Multi-cell Tubes and Honeycombs by Utilizing Key Performance Indicators [J]. Materials & Design, 2016, 89: 689-696.
[8] 周鑫美, 饶建强.多胞结构在汽车前纵梁中的应用研究[J]. 机械制造, 2010,48(1):37-39.
ZHOU Xinmei, RAO Jianqiang. Research on Application of Multi-cellular Structure in Auto Front Rails[J].Machinery, 2010,48(1):37-39.
[9] CHEN W, WIERZBICKI T. Relative Merits of Single-cell, Multi-cell and Foam-filled Thin-walled Structures in Energy Absorption [J]. Thin-walled Structures, 2001, 39(4):287-306.
[10] TABACU S. Analysis of Circular Tubes with Rectangular Multi-cell Insert under Oblique Impact Loads [J].Thin-walled Structures, 2016, 106:129-147.
[11] TANG Zhiliang, LIU Shutian, ZHANG Zonghua. Analysis of Energy Absorption Characteristics of Cylindrical Multi-cell Columns[J].Thin-walled Structures, 2013, 62:75-84.
[12] CUI Liang, KIERNAN S, GILCHRIST M D. Designing the Energy Absorption Capacity of Functionally Graded Foam Materials [J]. Materials Science and Engineering: A, 2009, 507(1/2): 215-225.
[13] SUN Guangyong, LI Guangyao, HOU Shujuan, et al. Crashworthiness Design for Functionally Graded Foam-filled Thin-walled Structures [J]. Materials Science and Engineering: A, 2010, 527(7/8):1911-1919.
[14] YIN Hanfeng, WEN Guilin, WU Xin. Crashworthiness Design of Functionally Graded Foam-filled Multi-cell Thin-walled Structures [J].Thin-walled Structures, 2014, 85(2):142-155.
[15] 林青霄.蜂窝材料填充薄壁结构的耐撞性分析研究与优化设计[D].厦门:华侨大学,2015.
LIN Qingxiao. Crashworthiness Analysis and Optimization Design of Honeycomb-filled Thin-walled Structures [D].Xiamen:Huaqiao University, 2015.
[16] 文桂林,孔祥正,尹汉锋,等.泡沫填充夹芯墙多胞结构的耐撞性多目标优化设计[J].振动与冲击,2015,34(5):115-121.
WEN Guilin, KONG Xiangzheng, YIN Hanfeng, et al.Multi-objective Crashworthiness Optimization Design of Foam-filled Sandwich Wall Multi-cell Structures[J].Journal of Vibration and Shock, 2015,34(5):115-121.
[17] TABACU S. Axial Crushing of Circular Structures with Rectangular Multi-cell Insert [J]. Thin-walled Structures, 2015, 95: 297-309.
[18] ZHANG Xiong, CHENG Gengdong, ZHANG Hui. Theoretical Prediction and Numerical Simulation of Multi-cell Square Thin-walled Structures[J].Thin-walled Structure, 2006, 44:1185-1189.
[19] LANGSETH M, HOPPERSTAD O S. Static and Dynamic Axial Crushing of Square Thin-walled Aluminium Extrusions [J].International Journal of Impact Engineering, 1996,18(7/8): 949-968.
