轮毂打磨5-DOF机械臂动力学建模与驱动参数预估
2018-03-06刘双勇王洪斌
荣 誉 刘双勇 王洪斌 韩 勇
1.燕山大学电气工程学院, 秦皇岛,0660042.河北科技师范学院 机电工程学院,秦皇岛,0660043.中信戴卡股份有限公司, 秦皇岛,066004
0 引言
金属材料表面打磨是机器人的主要应用领域之一[1-2]。铝合金轮毂是大规模生产型金属制品的典型代表[3-4],中国作为世界最大的汽车铝合金轮毂生产国,在铝合金轮毂制造的整个工艺过程中,压铸、锻造、机加、喷涂等工序均实现了无人化和智能化加工,但是,铝合金轮毂的打磨、抛光目前还是以人工加工为主[5-6]。有学者对机器打磨、抛光铝合金轮毂展开了研究,已有的铝合金轮毂打磨、抛光方法主要有两种:一种是采用通用工业机器人配手腕动力主轴的方式[7],这种方式通过在普通工业机器人手腕连接的主轴带动打磨叶轮旋转,实现对轮毂表面的打磨,但是,因为普通工业机器人一般采用串联结构,其自身的承载能力和刚度较差,而轮毂打磨的加工反作用力非常大,所以只有负载超过200 kg的大型工业机器人,才能满足轮毂打磨的力学要求,这导致此类系统建设成本非常高,而且效率非常低;另一种是采用专门设计的类似机床结构的打磨、抛光专机的方式[8-9],这种方式一般单独设计一种5轴联动机床,通过机床的电主轴带动打磨叶轮做伺服运动,实现对轮毂的打磨、抛光,但是,因为机床的数控系统需要单独开发,采用这种方式进行加工时,如何对电主轴进行轨迹规划编程与实现曲面贴合运动成为技术瓶颈,而且此类机床的体积非常庞大,不适合放在物流化、全智能的已有轮毂生产线。因此有必要设计一种专用的铝合金轮毂打磨机械臂,使其具有高负载、高冲击、高精度、复杂曲面贴合能力。
铝合金轮毂打磨需要工业机器人具有较高的刚度和承载能力,同时还需要具有较好的曲面贴合能力,这些都符合并联结构机械臂的特点。并联机构机械手方面的成果有TriVariant 机器人系列[10-11],李研彪[12]、金振林等[13]研制的混联构型机械臂,秦利[14]研制的空间机械臂等。通过对机器人进行动力学建模,可以有效获得其控制函数,并对其进行驱动参数预估。针对并联机构的动力学分析方法有Lagrange方程[15]、Newton-Euler方程[16]、虚功原理法[17]、Kane方程[18]等。
本文设计了专用于轮毂打磨的5-DOF并联机械臂,可以同时实现垂直和水平两种加工模式。
1 机械臂构型
本文提出的轮毂打磨5-DOF并联机械臂如图1所示,采用2-UPS+UPU构型,该构型包含3个分支,其中,1个是UPU分支,2个是UPS分支。UPU分支的两端均通过万向副连接到固定平台、运动平台;UPS分支通过万向副连接到固定平台,通过球面副连接到运动平台。其具体的运动副布局结构如图2所示。

1.机架 2.万向副电机 3.固定平台万向副 4.丝杠 5.丝杠螺母 6.丝杠电机 7.套筒 8.伸缩杆 9.运动平台万向副 10.球面副 11.运动平台 12.电主轴 13.打磨叶轮 14.轮毂 15.夹具图1 机械臂结构图Fig.1 Structure diagram of manipulator arm
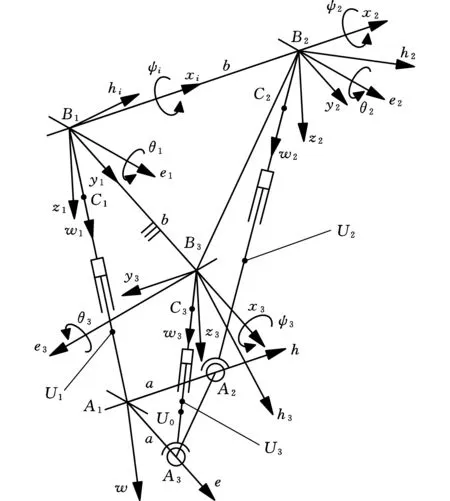
图2 机械臂2-UPS+UPU机构简图Fig.2 Sketch map of manipulator arm’s 2-UPS+UPU mechanism
采用约束螺旋法分析可知[19],该机构的UPU分支对运动平台施加1个约束力偶,其余2个UPS分支对运动平台无约束,故其运动平台有5个自由度(2个转动、3个平移)。确定每个分支的移动副为机械臂的移动驱动副、每个UPS分支的万向副靠近固定平台转轴为转动驱动副。
2 2-UPS+UPU机构的运动学分析
2.1 构型及坐标系的建立
将机械臂2-UPS+UPU机构进行参数化,从而建立通用模型:b=300 mm,a=90 mm,li∈(600,1 000)mm,i=1,2,3,h=800 mm。
在图2中,Bi(i=1,2,3)代表各分支与固定平台连接点,A1代表UPU分支与运动平台连接点,Ai(i=2,3)代表2个UPS分支与运动平台连接点,各连接点布局如图2所示。定义固定平台的结构参数A1A2=A1A3=a,运动平台的结构参数B1B2=B1B3=b,各支链的长度AiBi=li(i=1,2,3)。Ci(i=1,2,3)代表各分支的移动副套筒及附属部件质量中心,Ui(i=1,2,3)代表各分支的移动副伸缩杆及附属部件质量中心,U0代表运动平台的质量中心。
在固定平台定义坐标系B1x1y1z1,x1轴与对应万向副靠近固定平台的转轴共线;z1轴与固定平台平面垂直;y1轴符合右手法则。以Bi(i=2,3)为原点定义局部基坐标系Bixiyizi(i=2,3),xi轴与对应万向副靠近固定平台的转轴共线;zi轴与z1轴共线;yi轴符合右手法则。以A1为原点定义运动平台坐标系A1hew,其中w轴与运动平台的平面垂直;h轴与直线A1A2共线;e轴符合右手法则。在各分支定义本体运动坐标系Bihieiwi(i=1,2,3),其中wi轴与分支i的轴线共线;ei轴与其所在分支万向副远离固定平台的转轴共线;hi轴满足右手定则。
通过坐标变换可知,坐标系Bihieiwi(i=1,2,3)在坐标系Bixiyizi(i=1,2,3)中的姿态由两次旋转变换得到:第一次,绕xi轴旋转ψi;第二次,绕ei轴旋转θi。因此,ψi(i=2,3)就是机械臂的转动驱动输入角。为了方便建模,将A1确定为运动平台参考点。
2.2 运动学传递方程推导
在机械臂的基坐标系B1x1y1z1中构建封闭的矢量运动链:
(1)
式中,li、wi(i=1,2,3)分别为分支i的长度和主矢量;b2为B1B2对应矢量;b3为B1B3对应矢量;a2为A1A2对应矢量;a3为A1A3对应矢量。
计算式(1)关于时间t的导数,得
(2)
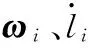
由wi·(ωi×wi)=0,将式(2)点乘wi,可得
(3)
(4)
简写为
(5)
其中,Jv∈R3×6。
按照角速度的运算规律,可得
(6)
式中,xi、ei分别为轴xi和轴ei在基坐标系B1x1y1z1中的主矢量。
将式(6)叉乘ei,可得
(7)
i=2,3
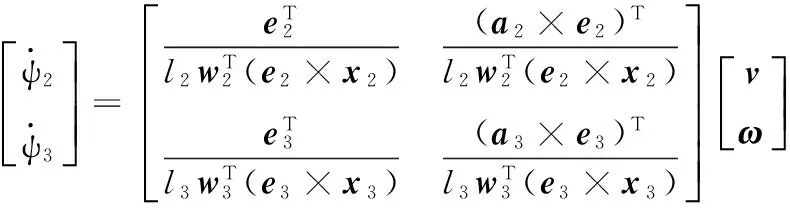
(8)
简写为
(9)
综合式(5)、式(9)可得机构速度映射关系为
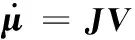
(10)
其中,J为雅可比矩阵,且J∈R5×6;μ为驱动速度。
可以通过推导构造R5×5雅可比矩阵,机械臂的运动平台在基坐标系Bx1y1z1中角速度ω=[ωxωyωz]T可以简化为ω′=[ωxωy]T,建立变换矩阵W,可以使V′=[vT(ω′)T]T与V=[vTωT]T的关系变为
V′=WV
(11)
W=[E5×5O5×1]
将式(11)代入式(10),可得

(12)
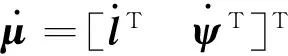
2.3 支链角速度描述
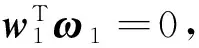
ω1=Jω1[vT(ω′)T]T
(13)

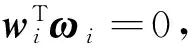
ωi=Jωi[vT(ω′)T]T
(14)
其中,E为三阶单位矩阵。
2.4 部件质心运动学描述
机械臂的各分支移动副套筒及附属部件的质心的速度可以通过万向副的转换求得
vi=liwi×ωi
(15)
式中,lCi为点Bi与点Ci之间距离。
机械臂的各分支移动副伸缩杆及附属部件的质心Ui(i=1,2,3)的矢量pUi为
(16)
式中,lUi为点Ai至点Ui的距离。
对式(16)关于时间求导,可得
vUi=JvUi[vT(ω′)T]T
(17)
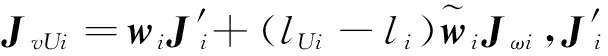
机构的运动平台质量中心U0在运动坐标系A1hew中的描述为pU0,运动平台质量中心的速度为
vU0=JvU0[vT(ω′)T]T
(18)

3 机械臂的动力学建模
3.1 广义力的定义
构造出运动平台参考点B1在基坐标系B1x1y1z1中的广义坐标p=[p1p2p3p4
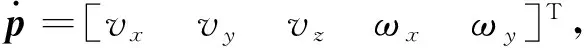
(19)

Q=(J′)Tτ
(20)
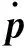
(21)
Jω0=[O2×3E2×2]
3.2 部件动能和势能描述
机械臂的部件可分成4种:各分支移动副伸缩杆;各分支移动副套筒;各分支丝杠及电机转子;运动平台。
各分支移动副伸缩杆在基坐标系B1x1y1z1中的动能方程为
(22)
式中,mUi为各分支移动副伸缩杆质量;IUi为各分支移动副伸缩杆相对于质心的转动惯量;vUi为各分支移动副伸缩杆的质心速度。
各分支移动副套筒在基坐标系B1x1y1z1中的动能方程为
(23)
式中,IBi为各分支移动副套筒绕万向副转轴的转动惯量。
各分支丝杠及电机转子在基坐标系B1x1y1z1中的动能方程为
(24)
式中,ISBi为各分支丝杠及电机转子绕万向副转轴的转动惯量;ISi为各分支丝杠及电机转子绕其自身轴线的转动惯量;ωSi为各分支丝杠及电机转子绕其自身轴线的角速度。
运动平台在基坐标系B1x1y1z1中的动能方程为
(25)
式中,mU0为运动平台的质量;IU0为运动平台绕过其质心的转动惯量;vU0运动平台的质心速度。
可以得到机械臂的总动能为
(26)
将式(22)~式(25)代入式(26)可得
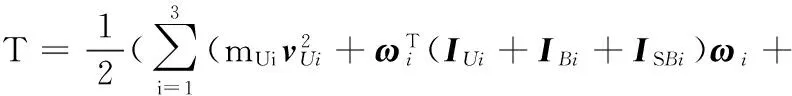
(27)
将式(13)、式(14)、式(17)~式(18)代入式(27)可得
(28)
式中,I为机构的等效广义转动惯量。
机械臂的系统的总势能为

(29)
式中,mi、qi分别为各分支移动副套筒及附属部件的质量和质心位置;mUi、qUi分别为各分支移动副伸缩杆及附属部件的质量和质心位置;mSi、qSi分别为各分支丝杠及电机转子的质量和质心位置;qU0为运动平台的质心位置。
3.3 机械臂的动力学模型
为机械臂构造拉格朗日函数:
L=T-V
(30)
式中,T为机械臂的动能;V为机械臂的势能。
根据拉格朗日方程可知
(31)
式中,pk为广义坐标;Fk为广义力。
将式(30)代入式(31),可得
(32)
式(32)可以整理为
(33)
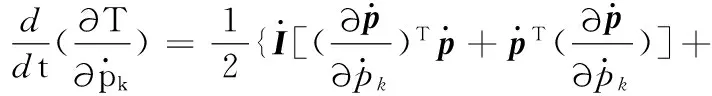
(34)
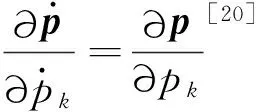

(35)

(36)
将式(36)整理成矢量表达,可得
(37)
H1=[H11H12H13H14H15]T
M1=[M11M12M13M14M15]T
K1=[K11K12K13K14K15]T
(38)
将式(38)整理成矢量表达,可得
(39)
M2=[M21M22M23M24M25]T
K2=[K21K22K23K24K25]T

(40)
整理式(40)可得

(41)
Kg=[Kg1Kg2Kg3Kg4Kg5]T
将式(37)、式(39)、式(41)代入式(35),可得
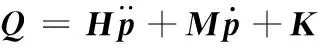
(42)
H=H1M=M1-M2K=K1-K2+Kg
式中,H为机械臂的转动惯量;M为机械臂的中间系数;K为机械臂的引力项。
将式(42)代入式(20),可得

(43)
τ=[τ1τ2τ3τ4τ5]T
其中,τ为机械臂的驱动力矩,G=((J′)T)-1。式(43)就是机械臂的逆动力学方程。
4 机械臂的伺服电机参数预估
4.1 参数预估模型
轮毂打磨机械臂的伺服电机工作峰值转速、力矩主要出现在以下几种工况:①机械臂静止并以最大加速度启动;②机械臂从最大速度状态进入急停;③在对轮毂打磨过程中沿曲线、曲面轨迹加工时的急转运动。在上述3种工况以外,机械臂是工作于恒力曲面贴合加工状态,此时机械臂是受到稳定的沿工件表面法向的加工力。
为了使分析条件与真实轮毂打磨一致,这里通过离线加工轨迹、力的规划软件Roboguide对轮毂的表面进行打磨加工轨迹、力的规划,生成轮毂表面的打磨加工轨迹曲线,如图3所示,其中,打磨轨迹曲线始终贴合轮毂表面的曲面,且加工轨迹的刀具z轴方向始终保持沿轮毂表面的法向,并保持沿此法向的加工力恒定。

1.打磨进入点 2.打磨结束点 3.打磨曲线4.轮毂 5.夹具图3 离线打磨轨迹规划图Fig.3 Trajectory planning diagram of off-line polish
通过Roboguide把图3中的打磨加工轨迹曲线转换为刀具轨迹函数,为了便于分析,这里把函数沿x轴、y轴两个方向分别生成,从而得到打磨加工轨迹函数vx(t)、vy(t)。同时,通过Roboguide把图3中的打磨加工的轮毂表面法向恒力在基坐标系中的函数也沿x轴、y轴两个方向分别生成,从而得到打磨加工力函数fx(t)、fy(t)。这样,就可以通过上述打磨加工轨迹、力的规划函数,进行伺服电机峰值参数预估。
4.2 伺服电机驱动转速分析
将式(12)的速度雅可比矩阵用向量描述:
(44)
式中,Jli为各分支移动驱动副速度向量,Jli∈R1×5;Jψi为分支i的万向副转动驱动角速度向量,Jψi∈R1×5。

(45)
将式(44)代入式(45),得到驱动电机与机械臂运动平台参考点A1的关系:
(46)
把轨迹vx(t)、vy(t)代入式(46)可得各驱动电机的转速:
(47)
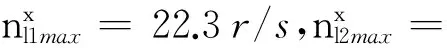
4.3 伺服电机驱动力矩分析
确定机械臂的力矩传递比是λli、λψi,各驱动电机输出扭矩εli、εψi(Nm)与机械臂的各分支移动驱动力及转动驱动力矩τli(N)、τψi(Nm)之间的函数为
(48)
将式(48)代入式(43),可得
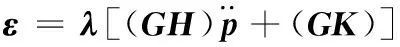
(49)
ε=[εl1εl2εl3εψ2εψ3]T

根据文献[10-11],机械臂的电机驱动力矩最大值函数为
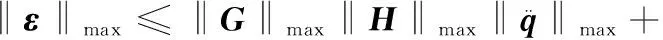
(50)
通过式(50)可以获得机构用以驱动打磨叶轮沿加工轨迹运动时(不考虑打磨加工表面法向恒力),3个移动驱动副伺服电机的最大驱动力矩εl1max=3.1 Nm,εl2max=3.7 Nm,εl3max=4.3 Nm;2个转动驱动副伺服电机的最大驱动力矩εψ2max=5.1 Nm,εψ3max=4.7 Nm。
仅考虑机构运动过程的电机驱动力矩是不全面的,还需要考虑打磨叶轮与轮毂之间沿法向的恒定加工力对机构驱动电机力矩的影响。将打磨加工力函数fx(t)、fy(t)代入式(43),就可以通过机构的动力学方程计算出打磨加工过程中每个驱动伺服电机的驱动力矩数值,从而间接计算出打磨加工过程中为抵消打磨叶轮法向恒定力产生的3个分支移动驱动电机的最大驱动力矩εl1max=0.5 Nm,εl2max=0.7 Nm,εl3max=0.9 Nm;2个转动驱动副伺服电机的最大驱动力矩εψ2max=1.1 Nm,εψ3max=0.7 Nm。
基于上述计算结果,将用于实现打磨叶轮运动和用于抵消打磨表面法向的力的2部分驱动力矩进行累加,可以得到3个移动驱动副伺服电机的最大驱动总力矩εl1max=3.6 Nm,εl2max=4.4 Nm,εl3max=5.2 Nm;2个转动驱动副伺服电机的最大驱动总力矩εψ2max=6.2 Nm,εψ3max=5.4 Nm,伺服电机驱动力矩最大值为6.2 Nm。
4.4 算例验证
为了验证伺服电机峰值预估模型的正确性,定义一组结构参数算例,见表1,通过算例验证预估值。

表1 轮毂打磨机械臂的算例参数
为了使机械臂在机构紧凑的同时具有较好的刚度,各主要构件采用铝合金材质,关键运动副的传动轴等高载荷部件采用中碳钢制造。因为沿x轴加工时产生的转速与力矩均大于其沿y轴加工时对应值,所以这里只分析其沿x轴加工时即轨迹函数vx(t)的电机驱动函数。
用工程计算软件对式(47)求解,可以获得本算例的伺服电机最大驱动转速值分别为nl1max=17.1 r/s,nl2max=17.8 r/s,nl3max=18.7 r/s,nψ2max=14.3 r/s,nψ3max=13.1 r/s。可见,这些数值均小于本文的理论预估峰值。
用工程计算软件对式(49)求解,并把打磨加工力函数fx(t)、fy(t)代入式(43),可以计算出本算例的3个移动驱动副伺服电机的最大驱动力矩的总和εl1max=2.73 Nm,εl2max=3.31 Nm,εl3max=4.08 Nm;2个转动驱动副伺服电机的最大驱动力矩总和εψ2max=4.73 Nm,εψ3max=3.71 Nm。这些数值均小于本文的理论预估峰值。
直接采用算例的峰值转速和力矩计算出伺服电机的功率为518 W,通过增加机械损耗因素,确定伺服电机的功率为700 W。
5 结论
(1)本文提出了一种用于轮毂打磨的5-DOF并联机械臂,采用多刚体系统的Lagrange方程推导出2-UPS+UPU机构的动力学方程,得到了机械臂的驱动输入量与运动平台输出量之间的动力学传递关系。
(2) 以机械臂的动力学方程为基础,推导出5个关节驱动电机驱动转速、力矩最大值计算模型,计算出各伺服电机转速最大值为25.1 r/s,力矩最大值为6.2 Nm。
(3) 选取一组具体机械臂的结构参数作为算例,计算出此算例的最大理论转速为18.7 r/s,最大理论力矩为4.73 mNm,确定伺服电机的选型功率为700 W。
[1] 黄田, 陈闯, 王辉. 一种新型并联动力头动力学参数辨识方法研究[J]. 机械工程学报, 2013, 49(19): 31-39.
HUANG Tian, CHEN Chuang, WANG Hui. Identification of Dynamic Parameters of a Novel 3-DOF Spindle Head[J]. Journal of Mechanical Engineering, 2013, 49(19): 31-39.
[2] 孙一兰, 柳洪义, 王品. 导弹弹体内壁打磨机器人及其运动轨迹规划[J]. 中国机械工程, 2009, 20(7): 838-843.
SUN Yilan, LIU Hongyi, WANG Pin. Design of Missile Inner-wall Grinding Robot and Its Trajectory Planning[J]. China Mechanical Engineering, 2009, 20(7): 838-843.
[3] 刘少凤, 孙宗禹. 全球制造策略[J]. 中国机械工程, 2001, 12(1): 114-119.
LIU Shaofeng, SUN Zongyu. Global Manufacturing Strategy[J]. China Mechanical Engineering, 2001, 12(1): 114-119.
[4] 张治民, 张星, 王强. 重型车辆传动行动构件轻量化设计研究[J]. 机械工程学报, 2012, 48(18): 67-71.
ZHANG Zhimin, ZHANG Xing, WANG Qiang. Research on Lightweight Design of Heavy Vehicle Transmission and Action Components[J]. Journal of Mechanical Engineering, 2012, 48(18): 67-71.
[5] 尹咸. 整体螺旋桨机器人砂带磨削加工工艺技术及试验研究[D]. 重庆: 重庆大学, 2015.
YIN Xian. Research on Technology and Control Scheme of Robotic Abrasive Belt Polishing for Integrated Propeller[D]. Chongqing: Chongqing University, 2015.
[6] 刘星. 铝合金轮毂局部难加工表面砂带抛磨方法研究[D]. 武汉: 华中科技大学, 2009.
LIU Xing. Research on a Method of Belt-polishing for Partial Hard-to-polish Surface of Al-alloy Wheel[D]. Wuhan: Huazhong University of Science and Technology, 2009.
[7] 杨仲升, 黄云, 邹莱. 铝合金轮毂机器人光整加工控制技术研究[J]. 中国机械工程, 2016, 27(14): 1857-1862.
YANG Zhongsheng, HUANG Yun, ZOU Lai. Analysis of Gas Flow Mechanism and Pressure Characteristics between Plates in Micro Scale[J]. China Mechanical Engineering, 2016, 27(14): 1857-1862.
[8] 赵菀. 汽车轮毂数控抛光机床的设计与研究[D]. 武汉: 华中科技大学, 2014.
ZHAO Yuan. Research and Design for NC Polishing Machine of Vehicle Wheels[D]. Wuhan: Huazhong University of Science and Technology, 2014.
[9] 王旭. 五轴数控抛光机CAM技术研究[D]. 秦皇岛: 燕山大学, 2011.
WANG Xu. Researching of Five-axis NC Polishing Maching CAM[D]. Qinhuangdao: Yanshan University, 2011.
[10] 黄田, 李曚, 吴孟丽. 可重构PKM模块的选型原则——理论与实践[J]. 机械工程学报, 2005, 41(8): 36-41.
HUANG Tian, LI Meng, WU Mengli. Criteria for Conceptual Design of Reconfigurable PKM Modules—Theory and Application[J]. Journal of Mechanical Engineering, 2005, 41(8): 36-41.
[11] 黄田, 李亚, 李思维. 一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计[J]. 中国科学, 2002, 32(5): 628-635.
HUANG Tian, LI Ya, LI Siwei. Criteria for Conceptual Design of Reconfigurable PKM Modules Theory and Application[J]. Science China Press, 2002, 32(5): 628-635.
[12] 李研彪. 新型6-DOF串并混联拟人机械臂的性能分析与设计[D]. 秦皇岛: 燕山大学, 2009.
LI Yanbiao. Analysis and Design of a Novel 6-DOF Hybrid Mechanical Arm[D]. Qinhuangdao: Yanshan University, 2009.
[13] 金振林, 曹舜, 高峰. 新型机器人肩关节及其运动学分析[J]. 中国机械工程, 2009, 20(14): 1639-1642.
JIN Zhenlin, CAO Shun, GAO Feng. Arc Spline Tool Path Generation for Triangular Mesh Surface Machining[J]. China Mechanical Engineering, 2009, 20(14): 1639-1642.
[14] 秦利. 考虑重力效应的空间机器人系统建模与控制研究[D]. 秦皇岛: 燕山大学, 2014.
QIN Li. Research on Modeling and Control for Space Robot System with Gravity Effect Consideration[D]. Qinhuangdao: Yanshan University, 2014.
[15] 王跃灵, 金振林, 李研彪. 球面3-RRR并联机构动力学建模与鲁棒-自适应迭代学习控制[J].机械工程学报, 2010,46(1): 68-73.
WANG Yueling, JIN Zhenlin, LI Yanbiao. Dynamic Modeling and Robust-adaptive Iterative Learning Control of 3-RRR Spherical Parallel Mechanism [J]. Journal of Mechanical Engineering, 2010, 46(1): 68-73.
[16] STAMPER R E. A Three Degree of Freedom Parallel Manipulator with Only Translational Degrees of Freedom [D]. Maryland: The University of Maryland, 1997: 83-97.
[17] TSAI L W. Solving the Inverse Dynamics of a Stewart-Gough Manipulator by the Principle of Virtual Work [J]. ASME Journal of Mechanical Design, 2000, 122(1): 3-9.
[18] SAMAK S M, GUPTA K C. Parametric Uncertainty on Manipulators Dynamics [J]. Mechanism and Machine Theory, 1998, 33(7): 945-956.
[19] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006:277-283.
HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced Spatial Mechanism [M]. Beijing: Higher Education Press, 2006: 277-283.
[20] 王振发. 分析力学[M].北京:科学出版社, 2002: 46-47.
WANG Zhenfa. Analytical Mechanics [M]. Beijing: Science Press, 2002: 46-47.
