外激振力作用下果树树干能量流

刘子龙, 王春耀, 许正芳, 张 智, 张姚斌

(新疆大学机械工程学院 乌鲁木齐，830047)

引 言

新疆是我国著名的瓜果之乡，林果业现已成为新疆经济发展的支柱产业[1]。随着瓜果种植面积的不断扩大，传统的人工采收方式因采摘效率低，造成部分成熟果实因不能及时采摘而坏掉，给果农带来了一定的经济损失，严重影响了果农的种植积极性。因此，迫切需要研究高效、快速的机械化采收装置。机械采收技术自20世纪60年代开始研究，到目前取到了较多的研究成果。文献[2]发现果树能量的传递与激振频率、激振位置和激振振幅有关。文献[3-5]认为果树不同的形态结构会不同程度地影响振动能量的传递，对果树进行合理的修剪，可以提高果实采摘效率。文献[6]利用自己研发的振摇树干式杏子收获机进行采摘试验时发现，当激振频率为15 Hz时，果实收获率最高达72%。Castro-Garciía等[7]利用频率可调树干振摇机采摘松果时发现，当激振频率在16.1～18.9 Hz时采摘率达85.7%。文献[8]运用模态分析研究了果树的振动参数、固有频率和阻尼比。文献[9-10]对振动式果品收获技术机理的国内外研究进展进行了系统论述,并通过试验发现作用在果树激振位置处的连续载荷比冲击载荷采摘效果更好。文献[11-12]发现,树枝的刚度随着直径的增大而增大，振动能量在刚度大的区域传递效率更高，进一步说明果实采摘效率与果枝的激振位置相关。在利用机械振动采收果实时，需要采收装置的工作部件在果枝某位置施加适当的载荷。外界输入的能量从激振位置传递到树枝与果实连接处，果实受迫产生一定频率和振幅的摆动，当其惯性力大于果实与果枝的结合力时,果实与果柄分离，完成采摘[13-14]。在实际采收过程中，果农往往通过延长采收机激振时间、增大激振振幅和激振频率来提高采摘效率，这种采收措施对树根、树枝和树皮都会造成一定程度伤害,导致果树来年减产[15]，从而带来一定的经济损失。笔者将果树视为一个系统并从能量的角度分析，外界对系统的激励就是对系统做功，其能量被储存到系统中，其中一部分能量转化为果枝的动能，另一部分因果枝内部阻尼结构和外界空气阻力等因素损失。

笔者通过研究海棠果树在不同激振频率和振幅作用下，能量从激振位置传递到果树树枝上的具体分布情况，分析果树形态结构(分叉角度、果枝直径)对振动能量传递的影响；通过田间采收试验，研究不同激振频率对果实采收效率的影响。

1 材料与方法

1.1 试验材料

选择3棵5年树龄的海棠果树作为试验样本。试验时间分别为2015年7月15日、2016年7月18日和2016年7月28日。本次试验在室内完成，根据果树在田间实际生长情况，树干根部用加持装置固定。果树在宏观形态结构是由主干、枝干、侧枝和树叶组成的分层结构。3棵样本树中两棵为“Y”型果树，包括树干、两根枝干和部分侧枝；1棵为三叉枝果树，包括树干、3根枝干和部分侧枝。A点为激振位置，如图1所示。在研究过程中对海棠果树做如下定义：由主干分生出第1层分枝为一级枝干，用bi表示；由第1层分枝生出第2层分枝为二级枝干，用ci表示。各样本树测点位置处直径如表1所示。

图1 各样本树结构图Fig.1 The structure diagram of each tree sample

1.2 仪器与设备

仪器设备主要包括振动试验台DC-600-6，SV-0505水平滑台、功率放大器SA-5，RC-300-2振动控制仪、DH5922N动态信号测试分析系统、三向加速度传感器DH311E、GHDAS软件、铁片和胶水等。

1.3 试验流程

设置振动试验台参数为正弦函数激振载荷，即x=Asin(2πft),其中：x为激振位移；A为最大激振振幅；f为激振频率。根据文献[8-9]，本次试验设置外界激振载荷频率f为10,12.5,15,17.5和20 Hz,振幅A为3,4和5 mm。设置DH5922N动态信号测试分析系统的采样频率为10 kHz[16]。相邻两测点间距为20 cm，图1中样本树1的测点3，4，5到分叉点的距离均为10 cm，即能量在相邻两测点之间的传递路径为20 cm。所有加速度传感器的安装方向与激振载荷方向一致，如图2所示。

表13棵样本树在测点处的直径

Tab.1Thediametersofthreesampletreesatthemeasuringpointmm

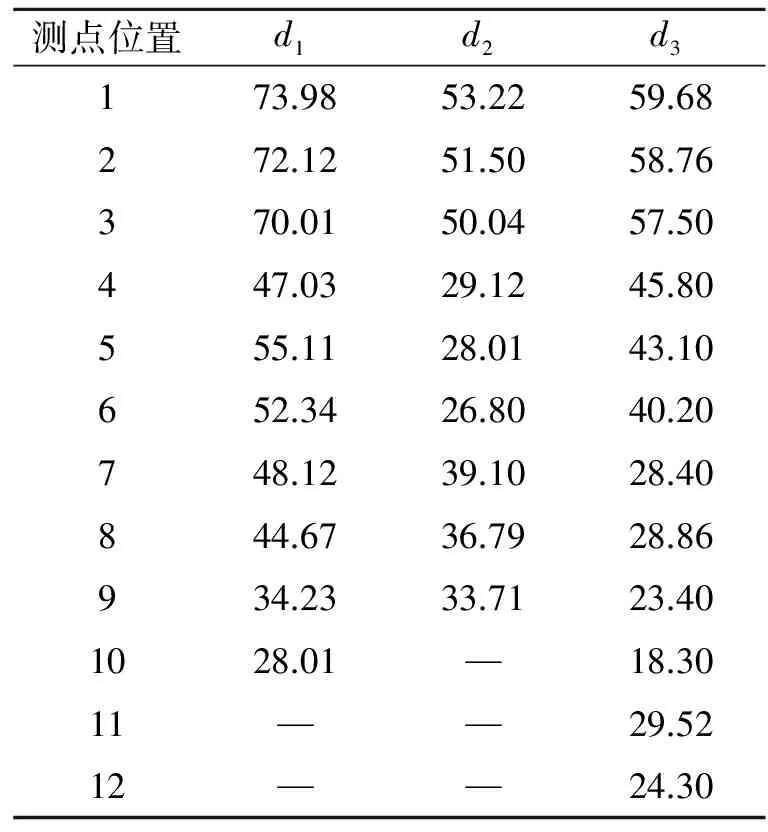
di(i=1,2,3)为样本树i在某测点直径

表2 3棵样本树分叉角度Tab.2 Bifurcation angle of three sample tree (°)

图2 加速度传感器的安装Fig.2 The installation of acceleration sensor

2 结果与分析2.1 加速度信号拟合

对测得的加速度信号进行曲线拟合，不同激振频率下加速度的拟合曲线及拟合函数如图3所示。

由图3可知，拟合后的加速度信号符合正弦函数变化规律，当激振频率f为10,12.5,15,17.5, 20 Hz时，各测点加速度拟合函数角频率ω随激振频率f的变化而变化，如表3所示。将f与ω拟合成曲线，如图4所示，可以得出f与ω呈线性关系。

图3 不同激振频率下的加速度拟合曲线Fig.3 Fitting curves of acceleration under different excitation frequencies

图4 激振频率与拟合函数角频率关系Fig.4 The relationship between the exciting frequency and the fitting function angular frequency

表3 激振频率f与拟合函数角频率ωTab.3 Excitation frequency and fitting function angular frequency

由图4可知，激振频率f与加速度拟合函数角频率ω的表达式为

2.2 动能方程及相对动能比

设各测点的加速度函数为

a(t)=Asin(ωt+φ)

(3)

则速度函数为

(4)

假设枝干密度ρ在各位置处相同，在测点i位置处枝干单位长度上的动能为

(5)

由于在激振频率相同的情况下，各测点的加速度拟合曲线周期相同，所以选择一个周期，即0到Tn(n=10,15,20)时间段内的动能进行比较

[cosφ-cos(ωTn+φ)]2

(6)

为了更准确描述能量在果枝上的分布，定义一个新的变量，相对动能比ki,j[10]，表示测点j处的动能与测点i处动能的比值，表达式为

(7)

其中：测点i为参考点。

3 分析与讨论

为了更准确地分析动能在果枝上的分布，选择离激振点最近的测点1为参考点，式(7)变形为

(8)

根据式(8)计算出在不同激振频率和不同激振位移作用下，各样本树的k1,j值如图5～7所示(纵坐标k1,j值单位为1，横坐标测点位置为无量纲单位)。从图5～7可以看出，能量在传递过程中不断被损耗，能量比值曲线分布由上往下依次为20，15和10Hz，说明20Hz与果树固有频率更为接近，果树更容易产生共振。各样本树的测点1，2，3均在主干上，与其他测点的能量比值进行比较可以看出，在主干位置上的能量传递效率高于侧枝上的能量传递效率，即果枝直径越大，能量传递效率越高。分别比较图5中的k1,3,k1,4,k1,5,k1,8,k1,9,k1,10值，图6中的k1,3,k1,4,k1,7值以及图7中的k1,3,k1,9,k1,11,k1,6,k1,7,k1,8值可以得出，能量在流经分叉点时产生分流，在节点处有所能量，并未完全流向果树分叉后的侧枝。样本树3的两侧枝与主干轴线的角度相近，即α1≈β1。从图7可以看出，在不同激振振幅和激振频率下，k1,9值始终大于k1,11值。可见，在分叉角度近似相等的情况下，能量更多的流向果枝直径大的一侧。

图5 样本树1在不同激振位移和不同激振频率下的k1j值Fig.5 The k1jvalues of sample tree 1 under different excitation displacement and excitation frequency

图6 样本树2在不同激振位移和不同激振频率下的k1j值Fig.6 The k1jvalues of sample tree 2 under different excitation displacement and excitation frequency

图7 样本树3在不同激振位移和不同激振频率下的k1j值 Fig.7 The k1j values of sample tree 3 under different excitation displacement and excitation frequency

4 田间果实脱离试验分析

为比较分析频率对果实采收效率的影响，设定3组激振频率分别为20，15，10 Hz的振动采收试验，每组选择30个生物特性相近的果实。图8为不同激振频率时的果实瞬时速度随时间变化曲线图。可以看出：激振频率为20 Hz时，果实脱落需要140 ms，果实最大瞬时速度峰值为3.46 m/s；激振频率为15 Hz时，果实脱落需要340 ms，果实最大瞬时速度峰值为2.84 m/s；激振频率为10 Hz时，果实脱落需要520 ms，果实最大瞬时速度峰值为2.27 m/s。由此可知，激振频率为20 Hz时，果实脱落时间最短。

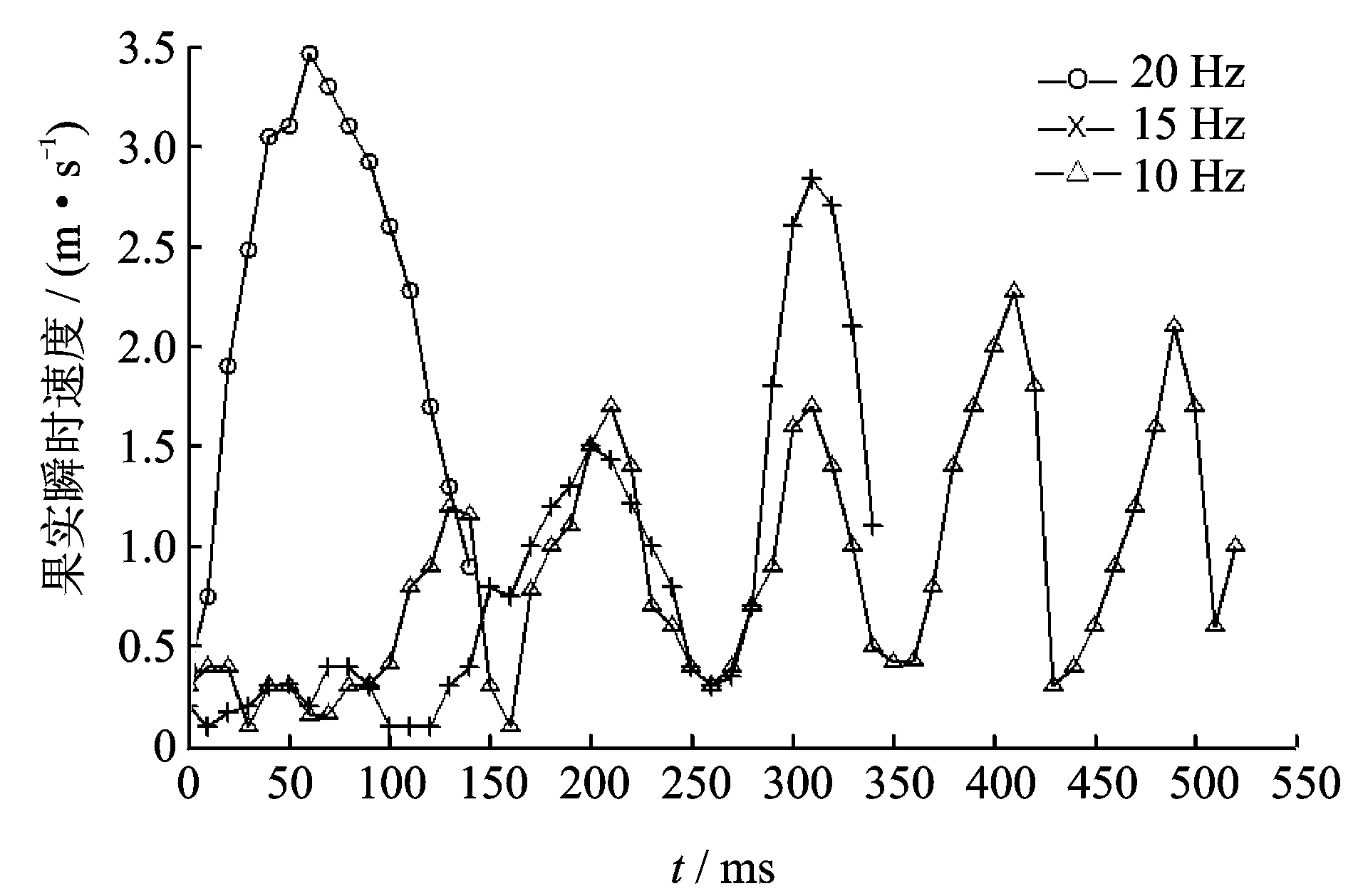
图8 不同激振频率作用下果实瞬时速度变化曲线Fig.8 The instantaneous velocity curve of at different excitation Frequency

图9为采收过程中果实在不同时刻的位置图,图(a)～(f)为果实在间隔2 ms后的运动图像。可以看出，果实在摆动过程中果柄相对树枝发生了弯曲和扭转，确定了果实的脱落是由于弯曲和扭转产生的惯性力大于果柄结合力，从而使果实脱落。激振频率为20 Hz时，通过观察高速摄像拍摄的果实运动图像可以看出，果实与树枝连接部分产生较大的振动速度和振幅，此时果柄与树枝连接位置处产生共振，果实更容易脱落。

5 结 论

1) 在正弦振动载荷激励下，果枝上的加速度值符合正弦函数变化规律，且果枝加速度信号频率与外界激振频率几乎一致。

2) 能量在果枝主干上的传递效率高于侧枝上的传递效率，即果枝刚度越大，能量传递效率越高。

3) 能量在流经分叉位置处产生分流，同时损失部分能量。当两侧枝与主干轴线的角度相近时，能量更多的分流到直径大的侧枝。

4) 采收过程中，果柄发生弯曲和扭转，果实上下左右摆动。激振频率为20 Hz时，果实最大瞬时速度和摆动幅度较大，果实更容易脱落。

[1] 陈虹.新疆统计年鉴[M].北京:中国统计出版社,2015: 433-434.

[2] Adrian P A, Fridley R B, Lorenzen C. Forced vibration of a tree limb[J]. Transactions of the American Soiety of Agricultural Engineering, 1965, 8(4):473-475.

[3] Chen S S，Shi J Y. Simplified model for vertical vibra-tions of surface foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(4): 651-655.

[4] Savary S K J U, Ehsani R, Schueller J K, et al. Simu-lation study of citrus tree canopy motion during harvesting using a canopy shaker[J]. American Society of Agricultural and Biological Engineers, 2010, 53(5):1373-1381.

[5] He Long，Zhou Jianfeng，Du Xiaoqiang，et al. Energy efficacy analysis of a mechanical shaker in sweet cherry harvesting[J]. Biosystems Engineering, 2013, 116(4):309-315.

[6] Mira T A，Martin B，Ortiz C，et al. Mechanical harvesting of processed apricots[J]. Applied Engineering in Agriculture，2006，22 (4): 499-506.

[7] Castro-García S, Blanco-Roldán G L, Gil-Ribes J A. Vibrational and operational parameters in mechanical cone harvesting of (pinus pineaL.)stone pine (pinus pineaL)[J]. Biosystems Engineering, 2012, 112(4): 352-358.

[8] Gil-Ribes J A，Castro-Garciía S，co-Roldán G L，et al. Dynamic analysis of olives trees in intensive orchards underforced vibration[J]. Trees, 2008, 22(6): 795-802.

[9] 陈都，杜小强，王书茂，等. 振动式果品收获技术机理分析及研究进展[J]. 农业工程学报, 2011, 27(8):195-200.

Chen Du，Du Xiaoqiang，Wang Shumao，et al.Mechanism of vibratory fruit harvest and review of current advance[J]. Transactions of the Chinese Soiety of Agricultural Engineering，2011, 27(8): 195-200.(in Chinese)

[10] Du Xiaoqiang，Chen Du，Zhang Qin. Dynamic responses of sweet cheery trees under vibratory excitations[J]. Biosystems Engineering, 2012, 111(3): 305-314.

[12] Zhou Jianfeng，He Long，Zhang Qin, et al. Effect of excitation position of a handheld shaker on fruit removal efficiency and damage in mechanical harvesting of sweet cherry[J]. Biosysems Engineering, 2014, 2(1): 36-44.

[13] 王业成，陈海涛，林清. 黑加仑采收装置参数的优化[J].农业工程学报, 2009, 25(3): 79-83.

Wang Yecheng, Chen Haitao, Lin Qing. Optinization of parameters of blackcurrant harvesting mechanism[J]. Transactions of the Chinese Soiety of Agricultural Engineering, 2009, 25(3): 79-83.(in Chinese)

[14] Mann D D, Petkau D S. Removal of sea buckthom (Hippophae rhamnoides L.)berries by shaking[J]. Canadian Biosystems Engineering, 2002, 43(2): 23-28.

[15] Affeldt H A，Marshal D E，Brown G K. Relative dynamic displacements withing a trunk shaker clamp[J]. Transactions of the American Soiety of Agricultural Engineering, 1988, 31(2): 323-330.

[16] 杨世锡，梁文军, 于保华. 基振动信号多通道同步正周期数据采集卡设计[J]. 振动、测试与诊断, 2013, 33(1): 23-28.

Yang Shixi, Liang Wengjun, Yu Baohua. Design of vibration signal′s multi-channel integer period synchronous acquisition card[J]. Journal of Vibration，Measurement & Diagnosis，2013，33(1): 23-28.(in Chinese)