地铁列车司机室前端结构耐撞性研究*

李少方， 侯本虎， 朱 涛， 肖守讷

(1 中车青岛四方机车车辆股份有限公司， 山东青岛 266111；2 西南交通大学 牵引动力国家重点实验室， 成都 610031)

随着我国城市轨道交通的快速发展，为方便人口流动以及满足人们的日常工作需求，地铁已成为人们生活和工作必不可少的一部分。特别是在大城市，客流量相对庞大，地铁运行的安全性受到了人们高度的重视，特别是在人口密集的市区中，更是不能忽视，地铁列车一旦发生碰撞事故，将带来无法弥补的巨大灾难[1]。在客运轨道车辆被动安全防护技术研究领域，欧洲标准委员会(CEN)颁布的EN 15227标准描述了轨道车辆在设计、运营、试验乃至事故发生时对车体耐撞性的要求[2]；王文斌等人建立了列车耐碰撞系统有限元和多体动力学联合仿真策略[3]；田红旗等人依照第2类Lagrange方程建立了列车撞击动力学方程，模拟列车车辆的撞击吸能情况[4]；肖守讷等人建立了列车纵向和垂向碰撞动力学耦合模型，利用不同材料模拟司机室前端吸能装置来研究其耐撞性，研究了高速列车和地铁列车在不同碰撞条件下列车辆的碰撞条件下列车辆的碰撞性能[5]；兆文忠和陈秉智等人研究车体安装假人的条件下，铝合金车体的二次碰撞以及前端结构抗碰撞性优化设计[6]。

目前大多的文献和研究人员以欧标EN 15227来评价和研究列车的耐撞性，但其中针对地铁列车的只要求在标准(AW0载荷+坐席乘客质量的50%)工况下车辆结构满足耐撞性要求。AW0载荷是指车辆处于空载状态，但对于目前中国大城市地铁的日运客量，特别是上下班高峰期以及节假日期间，只研究标准载客的耐碰撞性，已不能满足目前地铁列车对耐撞性的要求，故有必要对地铁列车在超载状态下的碰撞安全性进行研究。

以某地铁列车为例，建立地铁列车有限元模型以及列车动力学方程，模拟超载工况下(即：9人/m2)地铁列车耐碰撞性能[7]，在此基础上，对被动列车施加停放制动，研究列车在该载荷状态下的损坏情况，以及与不施加制动的对比结果，分析地铁列车的吸能特性和司乘人员的安全问题。

1 数学模型和理论方程的建立

列车碰撞是一个涉及结构非线性，接触非线性，弹塑性非线性等复杂的非线性大变形问题。文中建立了某地铁列车头车和中间车完整的有限元模型，模拟两列6节编组列车在直线轨道上的正面碰撞。表1为笔者给出的3种不同碰撞条件下的分析工况。

根据(AW0、AW1、AW2、AW3)的要求对空车车辆、坐席车辆、定员车辆、超员车辆的规定，文中除车体本身固有的质量外，其余质量(包括乘客和物品)均是通过建立质量点均分在车体底架上来进行实现。

表1 工况计算汇总表

为了对比的准确性，3种工况下主动车的速度均按照(25 km/h)来进行模拟，数学模型(图1)和动力学方程如式(1)～式(4)[8]：

图1 列车碰撞模型图

主动车辆：

(1)

(2)

被动车辆：

(3)

(4)

式中mi代表每辆车的质量(主动车辆从A6至A1，i=1,2…6；被动车辆从B1至B6,i=7,8…12)；ci代表车钩缓冲器的阻尼；ki代表车钩缓冲器的刚度，(i=1,2,3…n);fa代表主动列车的轮轨摩擦系数；fb代表被动列车的轮轨摩擦系数；

式中Fmi代表每辆车所受摩擦力；Fi代表界面力的大小；fd代表动摩擦系数；fs代表静摩擦系数。

2 有限元模型及动力学参数的建立

2.1 有限元模型的建立

根据某地铁列车的三维实体模型建立列车碰撞有限元模型，车辆车体采用由底架、侧墙、车顶、端墙、司机室(仅Tc车有)等构成的薄壁筒形整体承载结构，除司机室前端骨架采用不锈钢材料外，其他车体结构均采用铝合金材料，其中司机室外部由玻璃钢罩组成(这里不予模拟)。

该模型按其规定定义密度、弹性模量、泊松比、屈服应力和材料屈服后硬化的有效应力应变曲线等性能。通过定义车体模型与转向架模型间正确的连接关系以及建立各车辆有限元模型间钩缓装置进行耦合关联，最终形成连挂列车。

对于6节编组的列车碰撞，相关研究表明[10]：列车大部分碰撞动能主要靠前两节车吸收，因此为提高计算效率，列车头车及第1节中间车建立完整的有限元力学模型，其余车辆用刚体代替。

仿真模型考虑了地铁列车在碰撞过程中的头车前端结构和防爬吸能装置之间的碰撞冲击接触，轮轨之前的面面接触，转向架自身的接触和头车前端结构在碰撞压塑过程中的自身接触等[11]。列车主要的模型连接，以及轮轨接触如图2所示。

图2 有限元模型图

2.2 动力学仿真参数

为区分标准载荷列车和超员载荷列车在其载客上面的不同，表2列出了仿真计算中的车辆质量；有关第Ⅲ种工况，被动列车的停放制动，从摩擦学的观点来看，车辆的驱动与制动所需要的轮轨的摩擦小(在铁路上称为黏着)，在低速、干燥条件下，铁路钢轮与钢轨之间的黏着系数为0.3～0.5；在遇到降雨时，黏着系数会减小[12]，文中模拟列车在低速干燥条件下的运行情况，被动列车施加的摩擦系数取0.3。

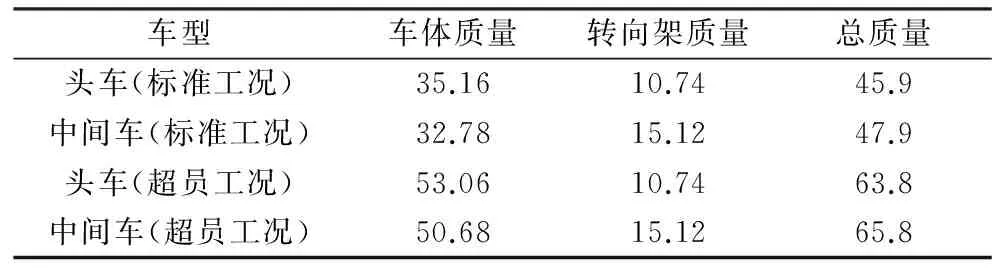
表2 配重列表 t

3 3种工况碰撞对比分析

3.1 司机室前端压溃区压缩量

根据上述信息，建立完整的有限元模型，导入LS-DYNA软件中进行仿真计算，在碰撞过程中，各主动车辆由初速度(25 km/h)撞击静止的同类型同配置的被动列车，主动列车逐步减速，而各被动车辆则由静止逐步加速，当仿真结果的速度曲线交汇以及碰撞能量吸收和剩余动能数值平稳时，视为碰撞结束。工况Ⅰ仿真时间0.85 s，工况Ⅱ仿真时间0.9 s，工况Ⅲ仿真时间1 s，头车车钩和司机室前端防爬吸能装置均充分吸收能量，随后司机室前端结构发生碰撞，如图3～图6表现了司机室前端压溃区的碰撞结果。

图3 定员工况碰撞初始时刻

图4 定员工况碰撞结束时刻

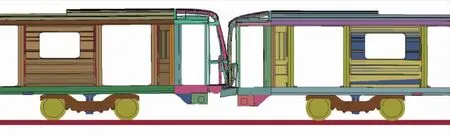
图5 超载工况碰撞结束时刻(无制动)

图6 超载工况碰撞结束时刻(有制动)

图7为被动列车司机室前端压溃区的长度与时间之间的关系，随着载客量的增加，被动列车司机室受压越来越严重其纵向最大受压距离分别为：58.67，284.99，452.86 mm。受压的被动车压溃区是司机安全的最后一道屏障，在超载状态下，被动列车压溃区基本已被侵占，452.86 mm的压溃距离也逐渐逼近压溃的极限600 mm。

图7 压溃区纵向长度变化量与时间特性曲线

3.2 司机室前端吸能

在列车碰撞过程中，主动列车在初始动能的驱使下向前推进，首先头车车钩压缩吸能，随后剪断并失效，接着防爬吸能装置啮合并切削吸能，同时产生热量(很少，忽略不计)，在防爬器压缩大约180 mm(单个总行程650 mm)行程后，车体结构开始接触，在3种工况下，在司机室前端产生碰撞后的最大界面力均为2 100 N左右，此时，防爬器和车体前端结构同时作用吸能。其能量吸收情况如表3所示，司机室前端压缩距离与吸能百分比的对比情况如表4所示。

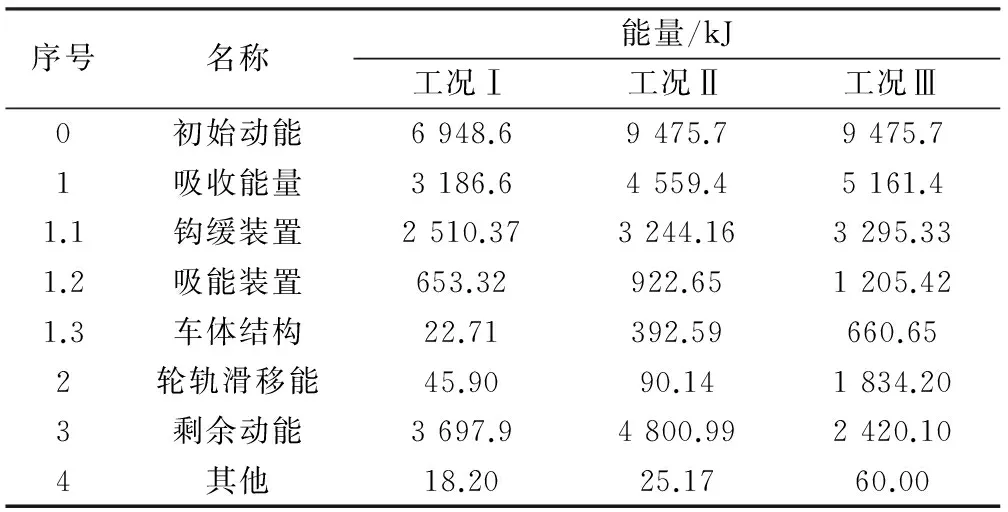
表3 列车碰撞能量吸收及耗散表

表4 列车碰撞能量吸收及耗散表

在列车碰撞过程中，撞击界面的吸能量占主要部分，头车车钩的行程和阻抗力都是一致的，防爬吸能装置的前180 mm也是在不同工况中吸能一致的，只有在司机室结构接触后，吸能才有所区别，其中第Ⅰ种工况，按照对地铁列车的一般要求，标准载荷条件下的碰撞对于司机室前端的压溃区结构基本没有影响，到碰撞结束时最大压缩量是58.67 mm，当载荷加大，到达超员载荷时，压缩距离逐渐加大，大约是总行程的一半， 最大压缩距离284.99 mm，在此基础上在被动列车施加停放制动，其碰撞程度达到最恶劣，司机室前端压溃区压缩距离逼近极限值，最大压缩距离452.86 mm，其前端对应的吸能距离660.65 mm(结构压溃后也需有一定的容量空间)也逼近极限压缩吸能容量。

4 结 论

基于建立的某地铁列车碰撞有限元模型，分析了在标准工况载荷，超员载荷以及施加停放制动的超员载荷这3种工况下，司机室前端的压溃破坏和列车整体能量吸收情况，得出以下结论；

(1) 在标准载荷和超员载荷下主动车以初速度(25 km/h)撞击同类静止无制动的被动列车，两种工况下司乘人员均为安全，而且司机室前端压溃区还有可供压缩的空间来保护司机室空间不受破坏；超员载荷下，司机室前端所被压缩的距离是标准条件下的5倍左右。

(2) 在同等初速的撞击条件下，被动车施加停放制动时，撞击的结果更为严重，司机室前端的车钩和防爬吸能装置均走完全程，被动车司机室前端的压溃区几乎被全部压溃，几乎是司机室前端压溃吸能的极限，在工况Ⅲ条件下，若再次加大速度即会对司机室空间产生威胁。

在地铁运营高峰期列车超员是很常见的现象，通过对3种工况的对比研究发现，对超员载荷条件下列车的碰撞安全性研究很有必要，以此评价所设计车辆结构的碰撞安全性，降低碰撞事故中的生命和财产损失。

[1] 雷成, 肖守讷, 罗世辉. 地铁列车头车耐碰撞性研究[J]. 城市轨道交通研究, 2013,16(11):32-35,39.

[2] 张乐乐，张啸雨，崔进，等. 地铁头车车体耐撞性仿真分析[J]. 铁道学报,2012,34(3):22-27.

[3] 王文斌，康康，赵洪伦. 列车耐碰撞系统有限元和多体动力学联合仿真[J]. 同济大学学报(自然科学版),2011,39(10):1552-1556.

[4] 田红旗，许平. 吸能列车与障碍物撞击过程的研究和分析[J]. 长沙铁道学院学报,2002, 20(3):55-60.

[5] 卢毓江，肖守讷，朱涛，等. 列车纵向-垂向碰撞动力学耦合模型建模与研究[J]. 铁道学报,2014, 36(12):6-13.

[6] 陈秉智，刘坤，汤海武，等. 铝合金车体前端结构抗撞击性优化设计[J]. 大连交通大学学报,2013,34(6):10-13.

[7] 池茂儒, 蒋益平, 张卫华,等. 长大重载列车系统动力学[J]. 交通运输工程学报, 2011，11(3):34-40.

[8] 赵倩，张锁怀. 地铁列车碰撞非线性动力学特性分析[J]. 陕西科技大学学报(自然科学版),2014,32(3):133-137.

[9] Varanis M, Mereles A. Mathematical model of a vehicle crash: A case study[J]. International Journal of Mechanical Engineering Education, 2017, 45(1): 89-100.

[10] 谢素超, 田红旗, 周辉. 耐冲击地铁车辆设计及整车碰撞研究[J]. 铁道科学与工程学报, 2008, 5(5): 65-70.

[11] 田光荣. 重载列车系统动力学研究[D]. 成都：西南交通大学, 2009.

[12] 大野薰，彭惠民. 轮轨间滚动摩擦及其控制[J]. 国外铁道车辆,2001,38(1): 36-40.