井周岩石的温敏效应及其对井壁稳定性的影响

武 博 朱忠喜 张永昌 雷万能 武兴勇 王 萌 朱元朔

（1.长江大学石油工程学院，湖北 武汉 430000；2.新疆塔中西部油田有限责任公司，新疆 库尔勒 841000；3.中国石油新疆油田公司工程技术研究院，新疆 克拉玛依 834000）

0 引言

钻井过程中，井内钻井液同近井地层进行热量传递，使井壁温度在纵向上和横向上有所改变，形成了以井眼为中心的温度场；同时井壁岩石受温度变化影响会热胀冷缩，当岩石的热胀冷缩受到限制时就会形成热应力。在以往井壁稳定性分析过程中未考虑因温度变化而产生的热应力对安全钻井的影响。笔者将明确热应力计算方法，并分析在有无热应力两种条件下井壁岩石的受力情况，通过比较分析来说明热应力在安全钻井过程中的指导意义。

1 井壁周围温度场分析

1.1 井筒温度场变化过程

钻井过程中，在泵压的作用下，地面将常温钻井液由钻柱注入，井底温度较高的钻井液由环空上返。钻井液循环过程中，不只是吸收井壁岩石能量，在距地表一定深度以上井壁岩石吸收钻井液的温度，将此深度定义为等温深度［1］。等温深度以下，地层给井周岩石传热，井周岩石与环空钻井液进行热量传递，环空钻井液与钻柱内流体进行热量交换。等温深度以上由环空循环液给近地层加热，并使井壁温度升高；同时给钻柱内钻井液加热。

图1表示井筒中钻井液热传递示意图，在y轴以上环空钻井液为传热源；在y轴以下地层为传热源。

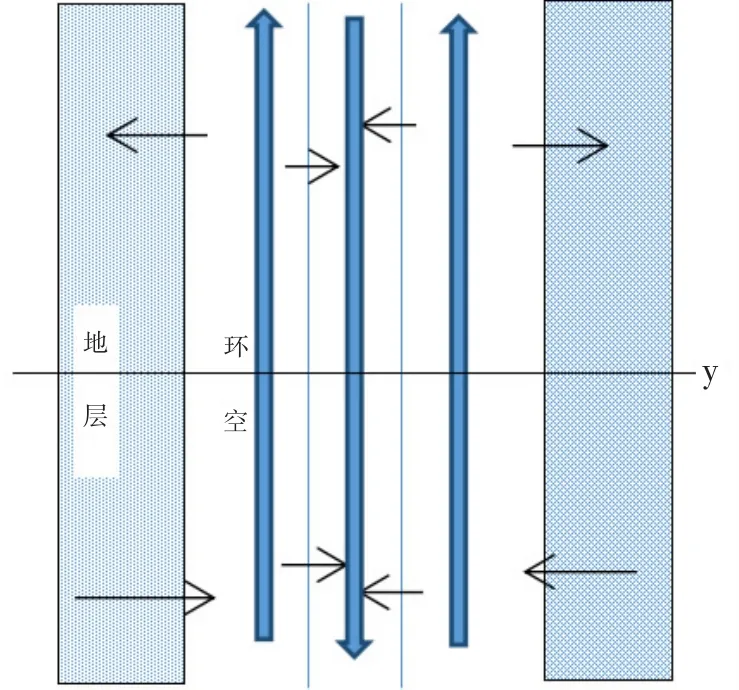
图1 井筒中的传热示意图

1.2 井筒温度场模拟分析

为更准确地描述此过程，可以运用传热学理论方程对钻柱、环空、井壁及地层的温度场进行表示。

假设：① 钻井液在钻柱和环空中的流动为一维流动，忽视流体的各参数沿周向和径向的变化，流体的温度只沿流体流动方向变化。② 将流体视为不可压缩流体，并忽视钻井液的物性和温度的关系。③ 钻柱的导热系数较大，热阻较小，可忽视钻柱内的温度变化。④ 流体流动中温度不断变化，轴向导热值较小，可以忽视流体的轴向导热。

钻柱内钻井液温度场方程［2］为：

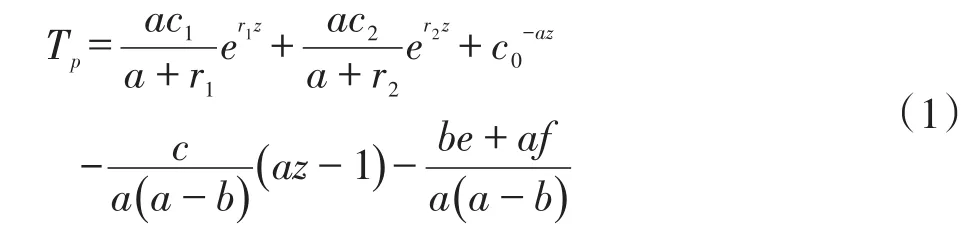
环空内钻井液的温度场方程为：

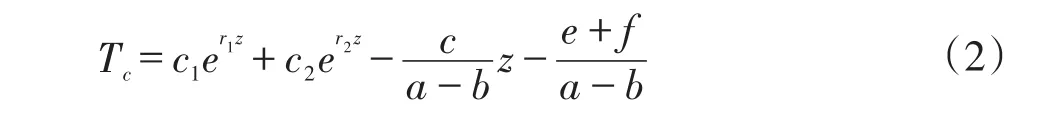
地层内导热方程为：

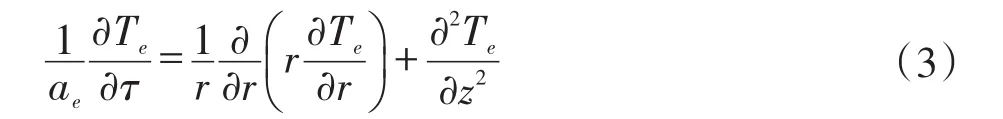
井壁岩石的温度场方程为：

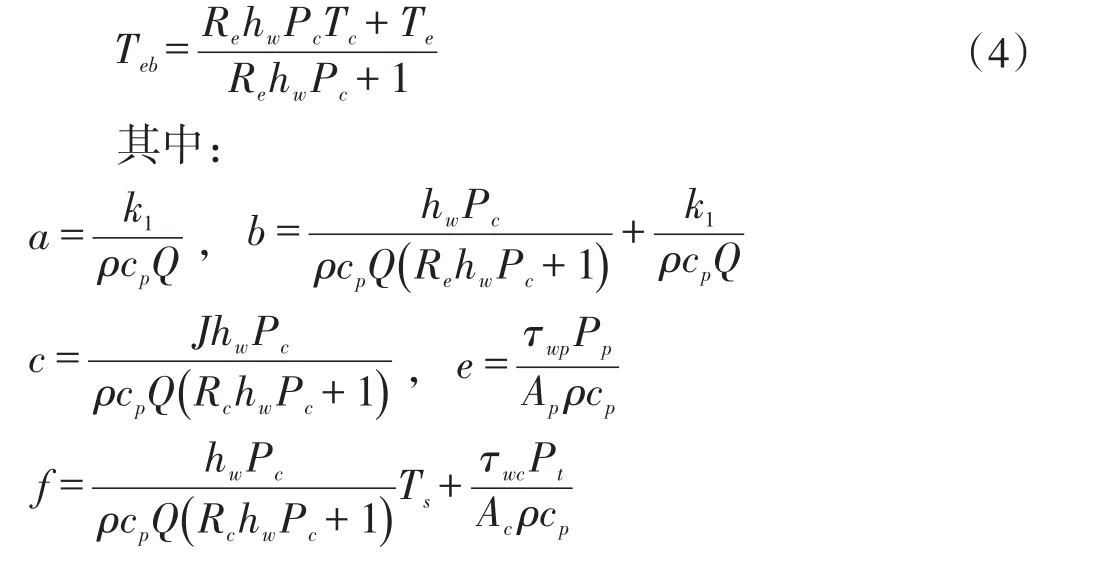
式中，Q为钻井液流量，L／s；z为井深，m；ρ为钻井液密度，g／cm3；cp为钻井液的热容，J／kg·℃；Tp为钻柱内钻井液的温度，℃；k1为钻井液单位长度传热系数，W／m·℃；Pp为钻柱内的湿周，m；Pc为井壁湿周，m；Ap为钻柱内的流动截面积，m2；Tc为环空钻井液温度，℃；hw为钻井液与井壁表面传热系数，W／m2·K；Teb为井壁温度，℃；Ts为地表温度，℃；Te为远离井筒处的地表温度，℃；τ为时间；τwp为管柱内粘性产生的井面摩擦力，MPa；τwc为环空内流体的壁面摩擦力，MPa；Pt为环空湿周，m；J为地温梯度，℃／m；Re为地层内导热热阻，（m·℃）／W；ɑe为地层的导温系数，m2／s；c1和c2为待定常数；r1和r2为特征方程的根；c0为积分常数。

根据表1中所给的某口井已知数据，应用上述方程模拟该井筒温度的变化，模拟结果如图2所示。图2可以证实前面讨论的传热过程，也可以看出等温深度大致在2 800 m，以等温深度为界限，上下井段的热量传递方向发生变化。井壁与地层之间的温度差值最大点不在井底，而在距离井底以上的某一深度。

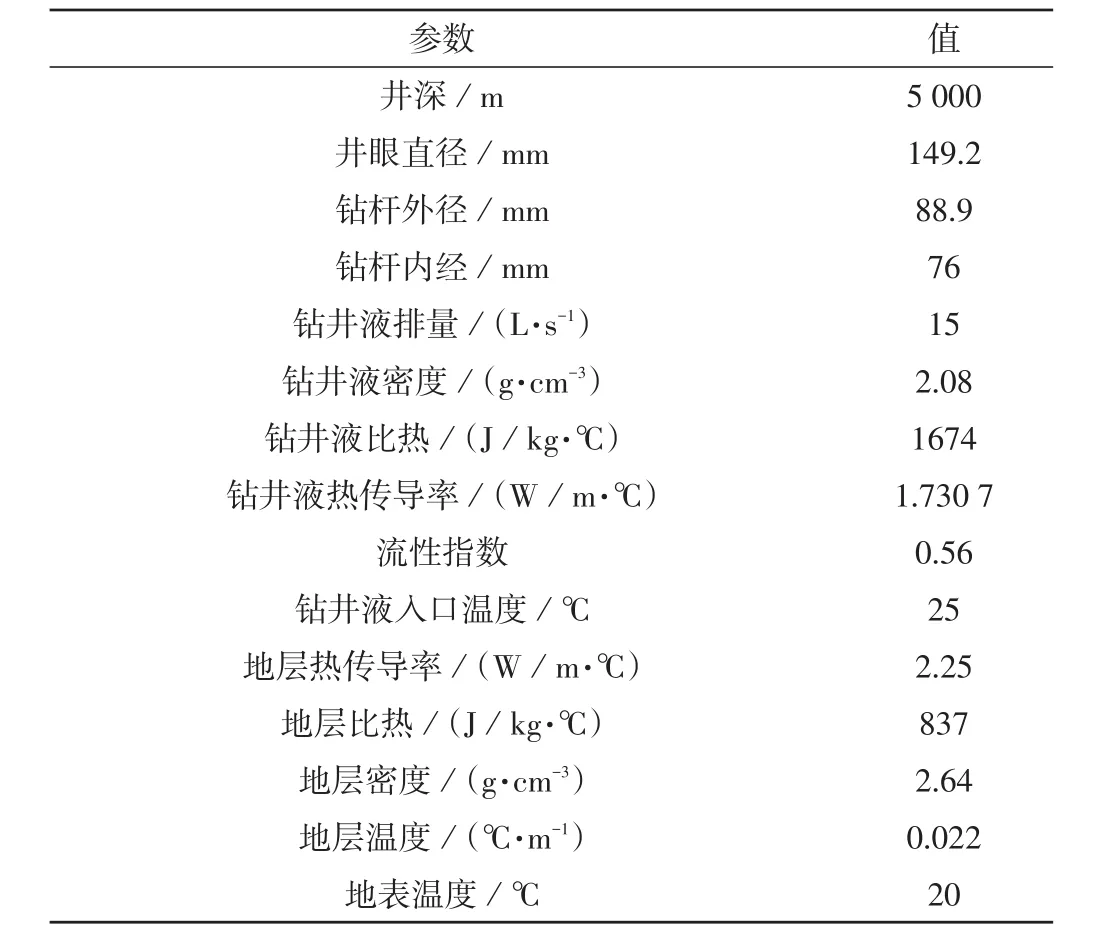
表1 某井已知参数表

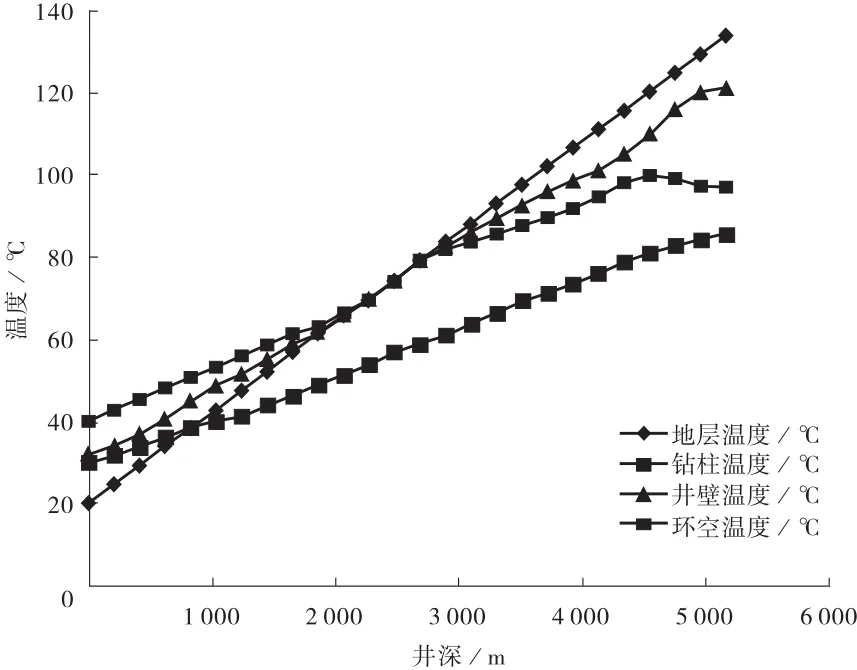
图2 井筒温度随深度的变化图

2 井壁周围应力场分析

2.1 井壁岩石的热应力

井周围岩石受到温度影响而引起的附加热应力，改变了井周围岩石的地应力分布状态，Roger J.Schoeppel运用全隐式的有限差分数值计算方法，对井筒中钻井液和地层的温度场的变化情况进行了深入分析［3］。依据热弹性理论温度变化引起的井周附加热应力场为：式中，σrT为温差下的径向应力，MPa；σθT为温差下的切向应力，MPa；σzT为温差下的垂向应力，MPa；T（r，t）为半径r处的地层温度，K；T0为某一深度井眼温度，K；aT为岩石的热膨胀系数；v为泊松比；E为弹性模量，MPa；re为井眼半径，m；r为岩石到井眼的轴向距离，m。

由式（5）～（7）可知，井壁面上的热应力只有轴向应力和切向应力。对中等硬度的岩石，如果要产生0.4 MPa的温差应力温度要相应的增加1℃，对于坚硬岩石这样的温度增加温差应力数值将会达到1 MPa。在4 000～5 000 m深的井中，循环和停止循环的温差会导致25～50 MPa的温差应力产生［4］。

2.2 井壁周围应力场

在钻井开始前，地下某一深度岩层在垂直压应力、水平压应力及孔隙压力的共同作用下处于平衡状态；当有井眼后，原始的平衡状态遭到破坏，井周岩石破坏最先发生在井壁，选取井壁岩石为分析对象来判断井壁的稳定性［5］。将地应力、热应力、孔隙压力和钻井循环液多力耦合得井壁处岩石的应力分布状态为：

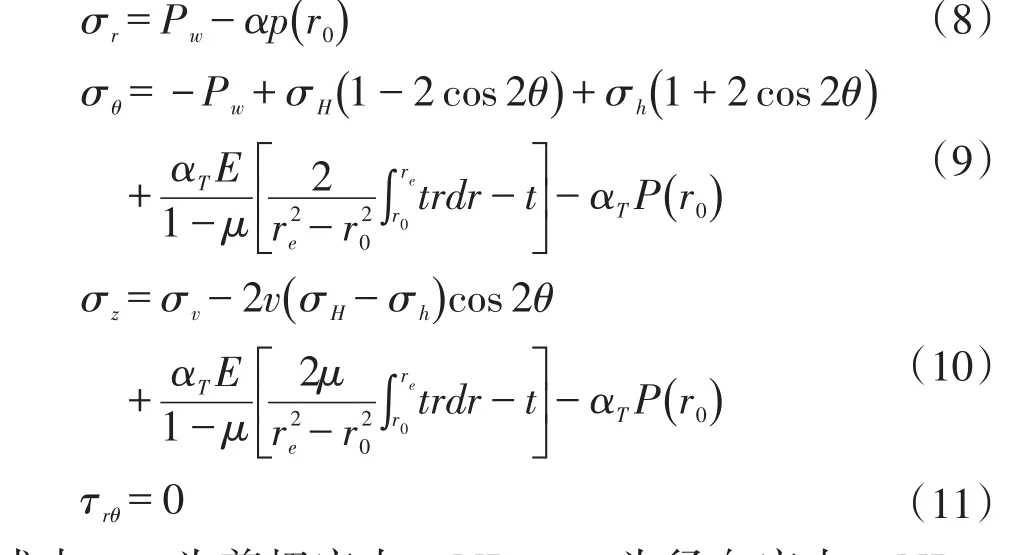
式中，τrθ为剪切应力，MPa；σr为径向应力，MPa；σz为垂向应力，MPa；σθ为切向应力，MPa；Pw为井眼内循环介质压力，MPa；αT为有效压力系数；P(r0)为距离井眼中心为r0的孔隙压力，MPa；σH、σh分别为地层水平最大主应力和地层水平最小主应力，MPa；μ为钻柱内钻井液的流速，m／s；θ为某点与井眼轴线的连线与最大水平地应力方向的夹角，（°）；t为温度引起的应变，mm；r0、E、v、t为r的函数。

将岩石在切向、轴向、法向上的应力经有效应力理论转化，求得井壁上主应力为：

式中，σ1、σ2、σ3分别为井壁上的最大、中间和最小有效主应力，MPa。

3 井眼周围岩石稳定性分析

研究岩石强度准则，可以进一步确定附加各种应力条件下围岩的稳定性。影响岩石强度的因素可以分为内因和外因。内因是沉积岩的成分、构造和结构等；外因为沉积岩所处的温度、压力等环境因素，因此岩石破坏形成极其复杂。就同一种岩层强度而言，不仅要从岩石力学和弹性力学角度进行分析，还要根据实验条件进行判断。

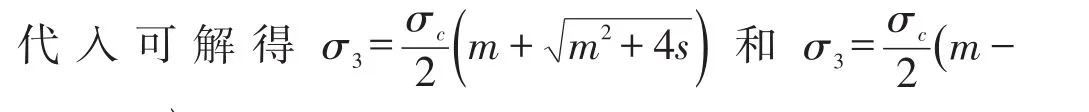
式中，σc为完整岩石的单轴抗压强度，MPa；σt为视抗拉强度，MPa；σs为视剪切强度，MPa；m、s为经验系数，m反映岩石的软硬程度，取值范围为0.001～25，s反映岩石的破碎程度，取值范围为0～1。

在已知井壁某点的主应力σ1、σ3时，若σ3＜σt，该点围岩发生拉伸破坏。若σ3＞σt，且σ1＞σs，该处围岩发生剪切破坏。

对应图2中模拟的井取4 000 m处的中硬砂岩地层，对井壁稳定性进行分析，见表2。

表2 井壁岩石强度分析对比表 MPa

在无热应力条件下，其中σ3＞σt，但σ1≤σs＝280.3 MPa所以井壁岩石不会发生剪切破坏。考虑热应力时，因为σ3＜σt，所以岩石在耦合热应力后会发生拉伸破坏。

4 结论

1）明确不同钻井工况下的井筒温度变化特征，给出钻柱内钻井液、环空钻井液、井壁及地层温度场的理论公式，通过数值模拟明确井壁与地层温差最大处位于井底以上的位置。

2）给出耦合热应力后的井壁岩石受力公式，得出井壁岩石主要受到轴向应力和切向应力。对于中硬岩石温度增加1℃，其内部会产生0.4 MPa的热应力，而对于坚硬岩石则会产生1 MPa热应力。

3）实例井中在4 000 m处考虑热应力后，井壁岩石的受力重新分布，使井壁失稳，充分证明了在深井钻井中必须考虑热应力的存在。

［1］张培丰.地层温度对科学超深井井壁稳定的影响［J］.探矿工程（岩土钻掘工程），2011，38（10）：1-5.

［2］李兆敏，黄善波.石油工程传热学：理论基础与应用［M］.北京：中国石油大学出版社，2008.

［3］吉源强.激光破岩井壁稳定性预测［D］.武汉：长江大学，2013.

［4］郭永宾，宋洵成.高温超压井地层破裂压力预测技术［D］.北京：中国石油大学，2010：9.

［5］王艳梅.温度对花岗岩力学性能影响实验研究及井壁稳定性的分析［D］.北京：中国地质大学，2012：23.