基于C-TTAHP方法的指控体系作战效能评估*

周中良 ，卢春光 ，赵 彬 ，潘 勃 ，肖 强

（1.空军工程大学航空航天工程学院，西安 710038；2.解放军95980部队，湖北 襄阳 441021；3.解放军93801部队，陕西 武功 710038）

0 引言

信息化海战是体系与体系的对抗，而指挥控制体系能力作为体系作战能力的核心要素必将直接影响体系作战能力的生成，因此，对基于信息系统的指挥控制体系能力进行评估对加快体系作战能力的迅速提升具有十分重要的现实意义［1］。

目前在指控能力作战效能评估研究方面，涌现了很多评估方法。文献［1］提出了模糊综合评判法，该方法能将很多难以量化的指标模糊化处理，缺点是利用精确的函数曲线代替隶属度函数，忽略了随机性；文献［2］将层次分析法与云模型结合起来很好地解决了复杂系统评估中存在的模糊性和随机性问题，但是层次分析法的判断矩阵是用精确的数据给出的，造成了语言评价信息的损失和不精确；文献［3］中提出了TOPSIS法，该方法充分利用原始数据信息，消除了不同量纲带来的影响，缺点是在多因素分析的情况下，指标权重的确定难度较大。

本文借鉴已有的研究工作，针对模糊综合评判法中存在的不足，提出了基于云模型［4］和二元层次分析法［5］的综合评估方法。在评估过程中，该方法采用二元语义层次分析法确定各层指标的权重，并将云模型理论应用于评价集与指标之间的隶属度的确定中，再进行指标之间的聚合，最后得到了评估结果。

1 指控体系能力作战效能指标体系

本文借鉴系统工程层次结构展开图的思想，在分析指控系统的组成单元、作战使用主体等方面的基础上，按照自顶向下，层层推进，逐步细化的思路构建了具有层次化递阶结构的指挥控制体系能力作战效能指标体系，如图1所示。

2 基于云模型和二元语义层次分析法的指控体系能力综合评估

基于云模型和二元语义层次分析法的指挥控制体系能力的综合评估方法主要包括评价集云模型、各层指标隶属度的云模型以及基于二元语义层次分析法的各层指标权重的确定3部分内容。具体的研究思路如图2所示。

2.1 云模型理论

定义1：云模型设U是一个定量论域，C是U上的定性概念，某一定量值x∈U，x对C所表示的定性概念的隶属度为μC（x），隶属度在论域U上的分布称为隶属云，简称云。μC（x）在［0，1］中取值，云是从论域U到区间［0，1］的映射，即：云的数字特征用期望值Ex、熵En、超熵He3个数值进行表示，记作N3（Ex，En，He），如下页图3所示。其中，Ex是论域空间中最能代表这个定性概念的点，是这个概念量化的最典型的样本，也叫期望；En代表一个定性概念的可度量粒度，反映了定性概念的不确定性和随机性，通常熵越大，概念越宏观；He是熵的不确定性度量，也叫超熵，它反映定性概念值的样本出现的随机性，揭示了模糊性和随机性的关联，云的厚度越大，云滴的离散度越大［6-7］。

2.2 二元语义层次分析法

2.3 评语集云模型的建立

确定评价对象的等级是指挥控制体系能力综合评估的关键所在。通常，通过前期广泛征求专家的意见，采用由m个评语组成的评价集来评价多层次结构中的各个指标元素，评语集为。

假设评语值的取值范围为［0，1］，将区间分成m个子空间，其中第i个子空间为。

算法1（评价集云模型的生成）输入m个子空间；输出评价云PJCi（Exi，Eni，Hei），其中。

Step1：根据各区间的上下限值，判断其为双边约束还是单边约束，计算Exi。

Step2：根据上一步计算的结果，计算Eni。

2.4 基于二元语义层次分析法的权重确定

算法2（基于改进的二元语义层次分析法的权重确定）输入判断矩阵B；输出指标权重W。

Step1：确定判断矩阵Bk的过渡矩阵Rk

应用式（6）计算二元语义判断矩阵Bk的过渡矩阵 Rk，且 Rk是模糊互补判断矩阵［9］。

Step2：获得一致性判断矩阵

计算模糊判断矩阵Rk的一致性指标ρk：

当ρk=0时，则模糊互补判断矩阵Rk满足一致性；否则，需要对模糊互补判断矩阵进行修正［8］，使其满足一致性。为方便起见，不妨将模糊互补矩阵均用矩阵R表示，具体的修正步骤如下：

2）计算由 R（t）生成的可达矩阵 T（t），若相容性指标，且 T（t）对角线元素为 0 时，停止；否则，转为下一步［8］；

4）转式（2）；

6）直至满足条件，将最终得到的满意一致性矩阵记为Vk。将调整算法分别应用到过渡矩阵中，得到满意一致性矩阵。V1，…，Vq。

2.5 指标隶属度云模型特征值的确定

假设被评价对象有n个属性，N个专家对指标属性进行评价，得到相应的评价矩阵（R）N×n，若将每个评价看作一个云滴，根据云模型理论则可生成n个隶属云。

算法 3（指标隶属云的生成）输入评价矩阵（R）N×n，计算隶属云的数字特征，生成云滴数为num；输出num个云滴及隶属度μ。

Step1：根据评价矩阵（R）N×n，采用式（11）计算隶属云的数字特征。

Step2：产生1个均值为Eni，标准差为Hei的正态随机数；

Step3：产生1个均值为Exi，标准差为Eni的正态随机数；

Step4：产生1个均值为Exi，标准差为Eni的正态随机数；

Step5：具有确定度μi的成为xi数域中的一个云滴；

Step6：重复步骤Step1～Step5，直至产生要求的num个云滴为止。

2.6 指控体系能力的综合评估

在已知各个指标的隶属云的数字特征值以及对应的指标权重的基础上，由式（12）计算出上一层指标的隶属云的数字特征，依此类推，可求得指挥控制体系能力的综合评价云：

式中：n为属性个数；wi为属性对应的权重。由式（12）即可确定指挥控制体系能力的综合评价云的数字特征值；然后在此基础上，计算出综合评价云与评价云之间的相似度［10］，确定与综合评价云最为接近的评价云，最终得到综合评价结果。

Step2：在评价云PJC1中生成以Ex1为期望和Enj为标准差的正态随机数；

Step4：重复步骤 Step2～Step3，直至产生 n 个 μj；

通过该算法计算评价云与综合评价云之间的相似度δ。

3 实例分析

根据上述建立的指挥控制体系能力指标体系，采用云模型以及改进的二元语义层次分析法对指挥控制体系能力进行综合评估。

3.1 评价集的云模型

根据前期征求专家的意见将评估语定义为7个等级：非常好、很好、好、一般、差、很差、非常差。评价等级具体的量化标准如下页表1所示。

其中对于非常差、非常好两个评价等级分别采用半降、半升云进行描述，而其他的5个评价等级则采用完整云进行描述，采用算法1所得的评价云图如图4所示。

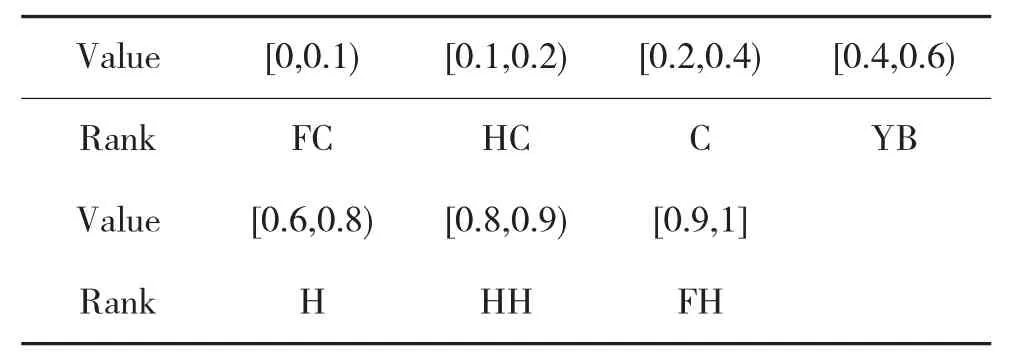
表1 评价等级标准

3.2 指标权重的确定

采用改进的二元语义层次分析法则可确定指挥控制体系能力中各个指标的权重，取，依据算法2确定指标权重，如表2～表4所示。

表2 Ui指标权重

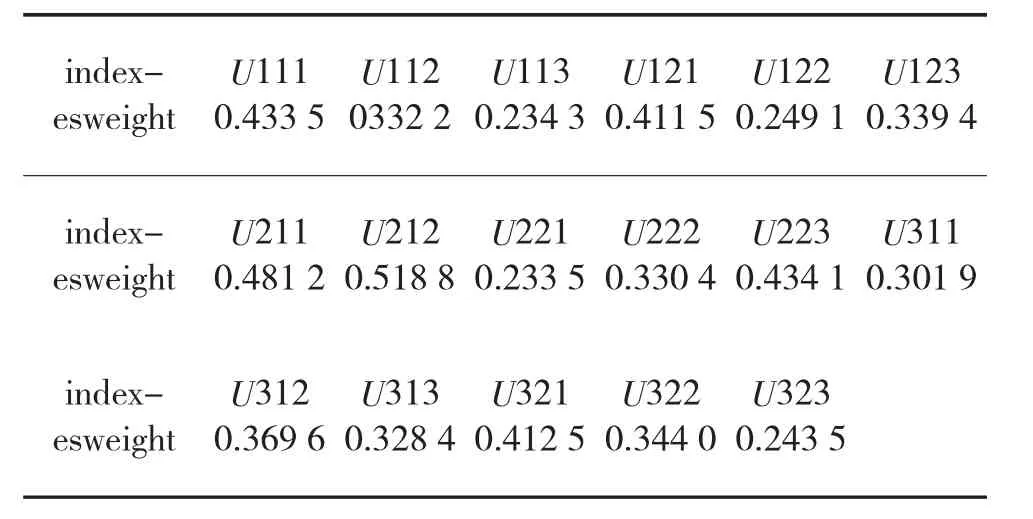
表4 Uijk指标权重

3.3 指标隶属云

根据建立的评语集，依据5位专家对指挥控制体系能力指标的理解，确定底层单因素指标的评价矩阵，评价结果如下所示：

通过采用算法3计算求得的每一项指标的期望值、熵和超熵，如下页表5所示。

3.4 指控体系能力的综合评估

根据表2～表4确定的指标权重以及表5确定的指标层每一项指标云模型的期望值、熵、和超熵，采用式（12）依次计算指挥控制体系能力指标体系中的各层指标云模型的数字特征，最终确定综合评估结果。如表6、表7所示。

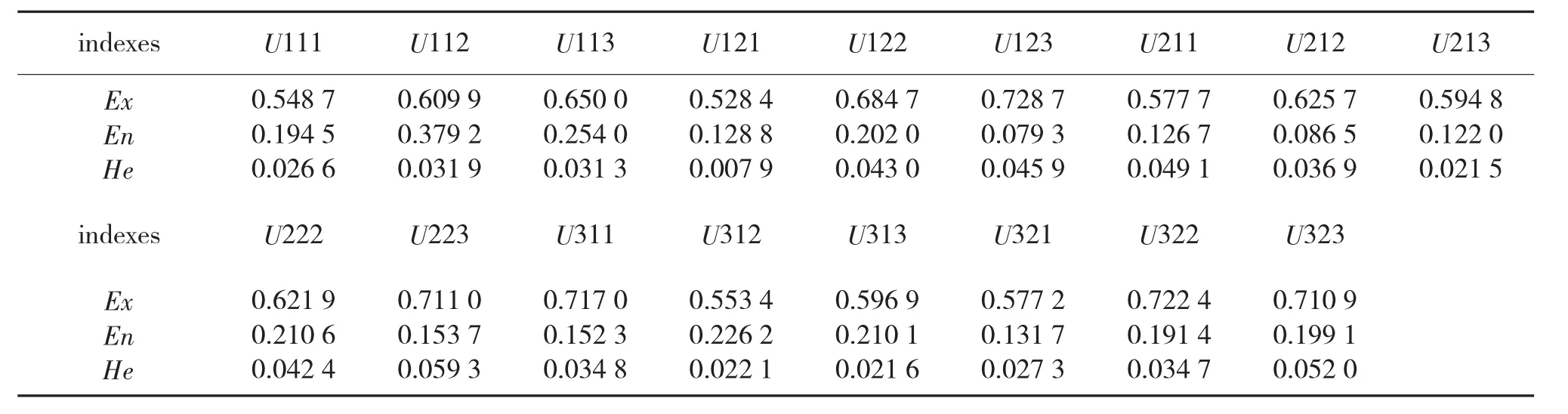
表5 Uijk指标的云模型数字特征值

表6 Uij指标的云模型数字特征值

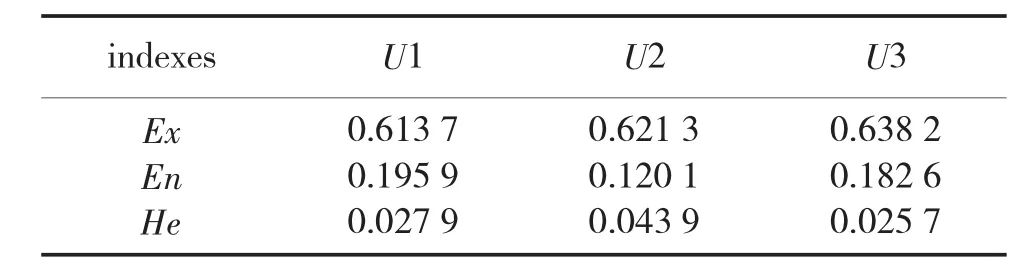
表7 Ui指标的云模型数字特征值

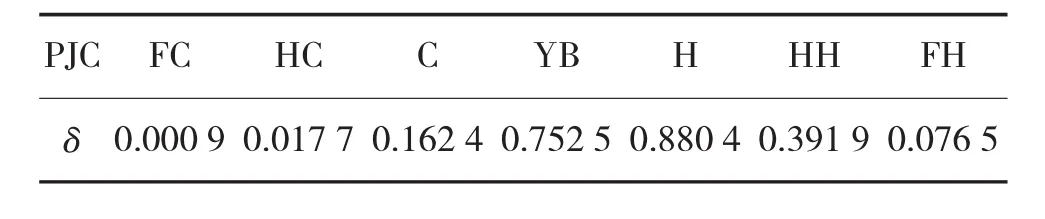
表8 综合评价云与评价云之间的相似度

根据算法4计算综合评价云与评价云之间的相似度δ，如表8所示。根据综合评价云与评价云之间的相似度可知，综合评价云与“好”评价云相似度最高，则可确定指挥控制体系能力的综合评价结果为“好”。

4 结论

本文针对指挥控制体系能力复杂性高这一难点问题，提出了一种基于云模型和二元语义层次分析法的综合作战效能评估方法。该方法可实现定性评价到定量评价之间的转换，有利于进一步解决评估过程中存在的模糊性、随机性，以及权重确定过程中出现的语言评价信息集结和运算中出现的信息损失和扭曲等问题，对多层次、多因素问题评估效果良好，为评估指挥控制体系能力提供了很好的思路，但评估指标的合理性、完备性和可操作性以及评语等级区间的设定仍需进一步研究。

［1］蒋启泽，蒋鹏.一种基于信息系统的指挥控制能力评估的方法［J］.舰船电子工程，2014，34（9）：35-37.

［2］付成华，杜修娟，赵川.基于AHP-云模型的土石坝老化病害风险分析［J］.西华大学学报（自然科学版），2016，35（5）：46-51.

［3］SU K，YU Q，ZHANG J.Research and application of gray relational effectiveness analysis based on TOPSIS［J］.IEEE GSIS2007，2007（2）：150-154.

［4］杜湘瑜，尹全军，黄柯棣，等.基于云模型的定性定量转换方法及其应用［J］. 系统工程与电子技术，2008，30（4）：772-776.

［5］游永彬，周延年，郑玉山.基于二元语义层次分析法的主观权重的确定算法［J］.西北工业大学学报，2013，31（5）：710-715.

［6］钟鸣.基于关联规则和云模型的水库诱发地震风险多层次模糊综合评价［D］.武汉：华中科技大学，2013.

［7］王威，田杰，马东辉，等.基于云模型的城市防震减灾能力综合评估方法［J］. 北京工业大学学报，2010，36（6）：764-770.

［8］吴小欢，吕跃进，杨芳.模糊互补判断矩阵的一致性检验及修正［J］.模糊系统与数学，2010，24（2）：105-111.

［9］张仕斌，许春香，安宇俊.基于云模型的风险评估方法研究［J］.电子科技大学学报，2013，42（1）：92-104.