基于AHP的履带机器人的综合性能评价*

2018-03-06张继明

火力与指挥控制 2018年2期

张军，张继明

（安徽理工大学机械工程学院，安徽淮南 232001）

0 引言

人们很早就开始对履带式移动机器人进行研究，不同的研究重点，侧重方向各不相同的话，所取得的效果也各有不同。由于履带式移动机器人能够很好地适应地面的变化，使得研究得以蓬勃发展，并且取得了重要成果，包括在机械结构设计、稳定性分析技术、探测技术、多传感器信息融合技术、导航和定位技术等方面的理论成果［1］，然而在对其综合性能的评价还处在探索阶段。

履带式移动机器人的性能评价是一个多目标决策问题，目前普遍的评价方法有灰色聚类法［2］、主成分分析法（Principal Components Analysis，PCA）［3］、层次分析法（Analytic Hierarchy Process，AHP）［4］、模糊评价法［5］等。因为履带式移动机器人的性能指标有定性指标，也有定量指标，所以要选用将定性分析与定量分析相结合的方法，通过总结以往的综合评价方法，本文提出运用层次分析法对这一问题进行了分析。

1 AHP评价模型的建立

人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法（AHP）为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。其基本流程如图1所示。

1.1 建立层次结构

应用AHP分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。根据评价目标及各影响因素，将其划分为目标层、准则层和指标层等多个层次，在这个模型下复杂问题被分解为元素的组成部分，这些元素又按其属性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。

递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地层次数不受限制，每一层次中各元素所支配的元素一般不要超过9个。因为元素过多会给两两比较判断带来困难影响准确度。

1.2 构造判断矩阵

建立层次模型后，对各层的某一元素和其他元素进行相对重要性的比较，构造判断矩阵。判断矩阵是层次分析法的核心。判断矩阵是通过两两比较得出来的，以每2个方案（或子目标）的相对重要性为元素的矩阵称为判断矩阵

即每次取两个因子xi和xj，aij表示xi和xj对某因素Z的影响大小之比，如果决策者人为因子xi和因子xj同等重要，则aij=1，aji=1；如果因子xi比因子xj稍微重要，则aij=3，aji=1/3等等。层次分析法确定权重，采用1～9标度法，通过专家论证，将两两指标之间互相比较构成判断矩阵。对于判断矩阵A中元素aij可以按表1方法确定。

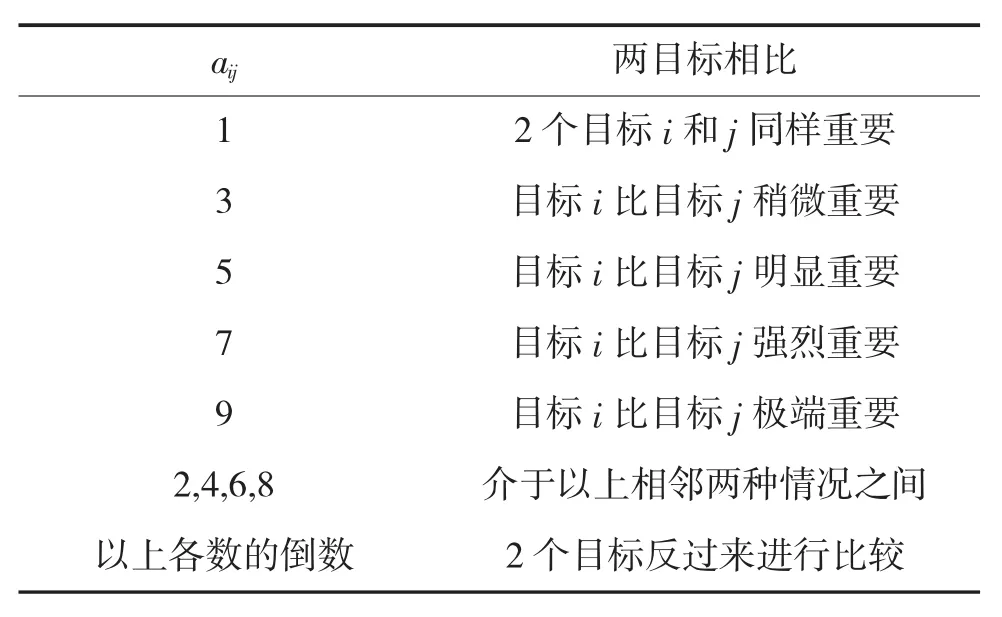
表1 层次分析法判断矩阵取值

1.3 层次单排序及一致性检验

1.3.1 层次单排序

由判断矩阵确定权重，可以有很多方法，下面介绍特征向量法中的和积法。

1）将判断矩阵每一列进行归一化处理

2）然后将每一列经归一化后的矩阵按行相加

3）将相加后的向量Mi进行归一化处理

所求得Wi即可作为相应的特征向量。

4）最后计算判断矩阵最大特征根

式中，（AW）i为向量AW第i个元素。

1.3.2 层次单排序的一致性检验

对判断矩阵的一致性检验步骤如下：

1）计算一致性指标CI

式中，n为判断矩阵的阶数。

2）查找相应的平均随机一致性指标RI，当n=1，2，…，9，可通过表 2 查得。

表2 平均随机一致性指标

3）计算一致性比例CR

CR越小，表示判断矩阵的一致性越好。当CR＜0.10时，认为判断矩阵的一致性是可以接受的，否则应对判断矩阵作适当的修改。

1.4 层次总排序及一致性检验

设上一层（A层）包含A1，…，Am共m个元素，其层次总排序权重分别为a1，…，am。下一层次（B层）包含n个因素B1，…，Bn，它们关于Aj的层次单排序权重分别为b1j，…，bnj（当Bi与Aj无关联时，bij=0）。则方案层各元素对总目标的组合权重为：

对层次总排序的一致性检验原理类似层次单排序一致性检验，其B层总排序随机一致性比例为：

当CR＜0.10时，认为层次总排序结果具有较满意的一致性并接受该分析结果。

2 AHP在履带式移动机器人综合评价中的应用

2.1 履带式移动机器人综合评价体系模型建立

评价体系是反映某一特定评价对象的较为完整的相互之间存在联系的评价指标，是对被评价对象全部或部分特征的真实反映，其准确反映事物的真实程度是评价结论准确可靠的保证。因此，建立合理的履带式移动机器人综合性能评价指标体系，需要充分考虑各因素之间的相互影响，考虑各性能参数的特点和相互间的制约。国内外学者对此已有一定的研究基础，借鉴前人的研究成果，结合履带式移动机器人的特点，遴选归纳出履带式移动机器人的性能指标，主要从生存能力，运动能力和通信控制能力3个方面进行描述，每类指标包含相应的子指标。

生存能力（B1），履带机器人保持在相应的恶劣环境下完好性的能力。主要包括持续工作能力B11，防水防腐能力B12，耐热抗冻能力B13。

运动能力（B2），履带机器人在正常情况下行驶所表现的能力。主要包括车体参数B21，地面适应能力B22，履带机器人的最高速度B23，最小转弯半径B24，履带装置对地面单位压力B25，最大跨越沟壕宽度B26，最大越障高度B27，最大爬坡角度B28，路径规划能力B29。

通信控制能力（B3），履带机器人在数据通信过程中，用于控制数据传输的能力。主要包括环境建模B31，建立通讯时间B32，数据传输正确率B33，最大无线通信控制距离B34，抗干扰能力B35，通信速度B36，自主控制能力 B37，故障诊断 B38。

综上所述，构建了履带机器人综合性能评价的层次模型如图2所示。

2.2 履带式移动机器人性能指标评估判断矩阵

根据图2的层次结构，经过专家的讨论，并结合表1的相关指标的度量值，可以分别得到准则层B对目标层A（记为A-B）、指标层C对准则层B（记为B-C）的指标的判断矩阵，如下：

A-B判断矩阵： B1-C判断矩阵：

B2-C判断矩阵：

表3 指标权重及其一致性检验

表4 各指标的组合权重

B3-C判断矩阵：

2.3 层次单排序及一致性检验

对于上面得到的判断矩阵进行计算，可以得出履带机器人综合性能在单一准则下的相对权重及一致性检验。具体计算如下：

对于矩阵A，利用前面求特征向量的和积法：

1）首先将矩阵的每一列进行归一化，得到矩阵：

2）然后将所得矩阵按行相加：

3）接下来将向量进行归一化处理：

4）最后可求判断矩阵的最大特征根：

由表2查得平均随机一致性指标RI1=0.58，因为一致性比例为，带入所求数据后得。

同理可得：

对于指标层C对准则层B（记为B-C）的指标权重结果及进行的一致性检验如表3所示。

由表3可知，指标层对准则层的指标权重结果大小情况，且每个矩阵的CR值均小于0.10，则一致性检验均通过。

2.4 层次总排序及一致性检验

利用上面的评价体系的模型及方法，对履带式移动机器人的综合性能进行评价，得出各指标的组合权重如表4所示。

由于总排序随机一致性比例为

3 结论

建立了对履带式移动机器人的评价指标体系，采用层次分析法（AHP），首先对其建立层次评价模型，构造出层次判断矩阵，将定性问题转化为定性与定量相结合的问题，同时解决了一致性检验问题；然后对判断矩阵进行层次单排序及一致性检验，可以得出准则层的权重大小情况；最后通过层次总排序及一致性检验，可以得出指标层的每个因素的权重大小排序情况，这一过程均可在MATLAB中编程实现。这种评价方法简化了分析过程，提高了决策效率，不仅为履带式机器人的综合性能评价提供了方法，而且为设计者提供了科学的参考依据。本文的评价模型可以推广到其他复杂的系统评价问题中。

［1］陈淑艳，陈文家.履带式移动机器人研究综述［J］.机电工程，2007，12（24）：109-112.

［2］史国庆，高晓光，吴梦舒.基于灰色聚类法的惯导仿真系统可信度评估［J］. 西北工业大学学报，2011，29（6）：960-964.

［3］赵京，李立明，尚红，等.基于主成分分析法的机械臂运动灵活性性能综合评价［J］. 机械工程学报，2014，50（3）：9-15.

［4］丁忠军，高翔，王成胜，等.基于层次分析法的载人深潜器潜航员职业特征研究［J］. 海洋工程，2014，32（6）：111-118.

［5］尚淑丽，顾正华，赵世凯，等.基于模糊逻辑的水电工程生态效应综合评价［J］.浙江大学学报（工学版），2014，48（9）：1603-1609.

［6］赵京，杨聪鹏，胡卫建.基于AHP-模糊综合评价法的轮履复合型搜索机器人性能评价及其软件开发［J］.北京工业大学学报，2016，42（6）：801-808.

［7］蒋耀.基于层次分析（AHP）的区域可持续发展综合评价：以青浦区为例［J］. 上海交通大学学报，2009，43（4）：566-571.

［8］蔡卫，吴兵.层次分析法在矿井通风评价中的应用［J］.辽宁工程技术大学学报，2005，24（2）：149-152.

［9］王建，黄凤岗，景韶光.AHP中判断矩阵一致性调整方法研究［J］.系统工程理论与实践，2005，25（8）：85-91.

［10］边浩然，资新运，王洪涛，等.基于变形履带的搜救侦察机器人设计与试验［J］.兵器装备工程学报，2017，38（3）：143-146.

［11］刘新宪，朱道立.选择与判断-AHP（层次分析法）决策［M］.上海：上海科学普及出版社，1990.

［12］谢季坚.模糊数学［M］.武汉：华中科技大学出版社，2006.