基于系统短期时序状态转移抽样法的孤岛运行微电网可靠性评估

彭寒梅， 郭颖聪， 昌 玲， 李帅虎， 李 辉

(1. 湘潭大学信息工程学院， 湖南 湘潭 411105；2. 湖南省风电装备与电能变换协同创新中心， 湖南 湘潭 411101)

1 引言

在目前能源短缺和环境恶化的大背景下，微电网越来越得到国内外的认可与发展[1-5]。微电网根据是否与外部电网相连接，可分为联网型和独立型微电网。微电网具有并网运行和孤岛运行两种基本运行模式。外部电网故障下，联网型微电网转为计划外孤岛运行模式，继续为微电网内重要负荷供电，以提高重要负荷的供电可靠性；为获取更好的效益，联网型微电网也可以主动脱离配电网，进入计划内孤岛运行模式，因此，有必要评估联网型微电网孤岛运行下的可靠性。独立型微电网一直工作于孤岛运行模式，完全利用自身的分布式电源(Distributed Generator，DG)满足微电网内负荷的供电需求，也有必要对其进行可靠性评估。

电力系统充裕度可靠性指在静态条件下，系统满足用户对电力和电能量需求的能力[6]。其按照时间长度可划分为长期可靠性评估和短期可靠性评估。短期可靠性评估考虑的时间尺度通常为小时、天、周或月级，其基于元件瞬时状态概率[7]。随着越来越多短期因素的出现，2004年IEEE PES会议再次强调了考虑安全特性的电力系统短期可靠性评估的重要性[8]。联网型微电网进入孤岛运行模式后的运行时间一般较短，其充裕度可靠性评估可认为是短期可靠性评估。微电网中利用间歇性可再生能源发电的DG的出力具有间歇性和随机性，输出功率随时间变化，且短期可靠性评估采用元件瞬时状态概率，其时变性导致系统状态也随时间变化，由此，孤岛运行微电网系统的短期可靠性指标值随运行时间变化，可靠性水平具有时变性。

目前，针对微电网长期可靠性评估的研究已取得了一定的成果[9-13]，而对微电网的短期可靠性评估研究不多。文献[14]提出了基于时变通用生成函数的孤岛运行微电网短期可靠性评估方法，但其属于解析法，且没有考虑静态安全约束的影响。电力系统充裕度可靠性是以故障下系统切负荷的概率及大小作为可靠性指标，传统上未考虑系统静态安全约束的影响。目前，已有文献在微电网经济调度方面考虑了静态安全约束[15,16]。传统静态安全约束问题中，主要考虑线路潮流约束和节点电压约束，而无平衡节点微电网系统的稳态频率是未知状态变量[17]，还需考虑稳态频率安全约束。节点电压幅值和稳态频率的大小会影响非故障区负荷的正常运行，可能导致非故障区负荷的切除，从而影响微电网充裕度可靠性评估的结果，因此，考虑静态安全约束的微电网充裕度可靠性评估结果更能反映系统实际的充裕度可靠性水平。

本文针对孤岛运行微电网短期可靠性评估的特点，提出一种孤岛运行微电网短期可靠性评估模拟法。提出系统短期时序状态转移抽样法及抽样过程；建立考虑控制策略的DG装置出力模型，再计及故障解列、储能装置充放电、孤岛系统切负荷及静态安全约束的影响进行孤岛运行微电网短期可靠性评估，得到包括负荷点平均停电时间在内的短期可靠性指标值。

2 系统短期时序状态转移抽样法

2.1 两状态元件的短期状态转移概率

电力系统中绝大部分元件为可修复元件，由此仅考虑可修复元件的可靠性。孤岛运行微电网的短期运行内，不考虑元件的计划停运，采用两状态可靠性模型，设状态空间为{0,1}，正常工作状态为状态0，故障状态为状态1。假设两状态元件的故障率和修复率为常数，元件的无故障工作时间和故障修复时间均服从指数分布，则元件状态转移过程为齐次马尔可夫过程[6]，可知：

(1)

式中，P(t)为t时刻元件各状态的概率；A为转移密度矩阵；λ为元件的故障率；μ为元件的修复率。

假设当前元件状态为工作状态，即P(0)=[1,0]，求解式(1)，可得元件在时间t后处于工作和故障状态的概率p00(t)和p01(t)为：

(2)

假设当前元件状态为故障状态，即P(0)=[0,1]，求解式(1)，可得元件在时间t后处于工作和故障状态的概率p10(t)和p11(t)为：

(3)

当时间t取较小值时，式(2)和式(3)与t相关，称此情况下概率为两状态元件的短期状态转移概率。进一步地，元件在[0,T1]时段内的平均不可用率Uavg为：

(4)

式中，P(0)为元件在t=0时刻的各状态概率。

2.2 系统短期时序状态转移抽样法及其抽样过程

设系统含有n个元件，微电网内元件数目较少，因此，在仅考虑1重故障下，共有n+1个系统状态。设x0为所有元件正常工作的系统状态，x1,x2,…,xn分别为元件k(k=1,2,…,n)发生故障所对应的系统状态，则系统状态空间为{x0,x1, …,xn}。设抽样间隔为Δt，在抽样间隔Δt内元件状态不发生转移，将Δt代入式(2)、式(3)，求解各个元件的短期状态转移概率，进而可计算得到含n个两状态元件的系统的短期状态转移概率矩阵PS(Δt)：

(5)

式中，pxixj(Δt)为系统的短期状态转移概率，即系统由状态xi经过时间Δt后转移到状态xj的概率，i,j=0,1,…,n，其值由式(6)可得：

(6)

由于仅考虑了1重故障的系统状态，PS(Δt)矩阵中各行元素之和均小于1。为保证抽样准确性，PS(Δt)矩阵中各元素应乘以其所属行的系数Li，Li由式(7)可得：

(7)

设t0时刻系统状态为xi(t0)，xi∈{x0,x1,…,xn}，产生在(0,1)区间上均匀分布的随机数ξ，得到Δt之后的系统状态xi(t0+Δt)为：

(8)

如果Δt后的系统状态未发生转移，则系统状态的停留时间增加Δt；如果系统状态发生转移，则获得新的系统状态，并重新开始统计系统状态停留时间。

如此以间隔Δt抽样系统状态，可得到孤岛运行时间T内的系统短期时序状态样本。Δt的选取必须使在这个时间中系统发生两次或多次转移的概率可以忽略不计，如果在任一特殊情况下无法确定Δt的取值，则可以先估计一个Δt的值，以这个值抽样系统并计算出可靠性结果，然后将Δt值减少再进行重复计算，并且继续这个过程，直到两组结果在可以接受的允许精度范围之内，从而确定Δt的取值。

3 考虑控制策略的DG装置出力模型

微电网中，大部分DG是通过电力电子接口接入，由DG、电力电子变换器、控制器、保护电路等构成DG装置，其控制策略主要有恒压恒频控制、恒功率控制和下垂控制。本文考虑的DG装置包括风力发电(Wind Turbine，WT)装置、光伏电池(Photovoltaic Cell，PV)装置和微型燃气轮机(Micro Turbine，MT)装置。WT、PV装置利用间歇性可再生能源发电，一般采用恒功率控制，为间歇性DG装置；MT装置利用非间歇性能源发电，可采用恒功率控制，也可采用恒压恒频控制或下垂控制，为非间歇性DG装置。但孤岛运行微电网中必须要有恒压恒频控制或下垂控制的DG装置。

正常工作状态下，恒功率控制的MT装置出力为指定值，恒压恒频控制或下垂控制的MT装置出力随系统功率平衡情况而变化。充裕度可靠性评估中，考虑元件故障下系统切负荷的情况，当系统满足功率平衡时认为不需切除负荷，因此，充裕度可靠性评估模型中，恒压恒频控制或下垂控制的MT装置用到的是其正常工作状态下的最大出力。

忽略WT装置的内部损耗，采用恒功率控制的WT装置正常工作状态下的出力与风速有关，可近似表示为：

(9)

式中，PWT(t)为t时刻WT装置的有功出力；v(t)为t时刻的风速；Pr为WT的额定功率；vci、vr、vco分别为切入风速、额定风速和切出风速。

采用恒功率控制的PV装置正常工作状态下的出力与光照总辐射量有关[18]：

(10)

式中，ηC为光电转换效率；I(t)为t时刻的光照总辐射量；SPV为光伏电池板面积；KC为阈值常数。

风速、光照总辐射量的预测模型已经很成熟，采用文献[19]提出的相似数据的支持向量机对短期风速进行预测，光照总辐射量采用文献[18]的方法进行预测。

4 孤岛运行微电网短期可靠性评估

4.1 计划解列及切负荷策略

为避免因微电网内部故障而引起整个微电网停电，微电网还须预备解列方案，一般是预先设置合理的解列点。目前微电网一般是辐射状拓扑结构，且考虑到功率平衡原则、电气分布、地理位置等因素，设置解列后形成两类孤岛系统：微电网级孤岛和主馈线级孤岛。微电网级孤岛为包含孤岛运行微电网部分或全部负荷及所有非故障DG装置的功率平衡区域，解列点设置在微电网的并网点上。主馈线级孤岛为包含一个或几个DG装置及其周边负荷的功率平衡区域，解列点设置在主馈线的开关器件上。

根据不同元件故障对负荷点供电情况的不同影响，将系统状态分为四种类型：①type1，系统正常工作状态；②type2，DG装置或储能装置故障状态；③type3，分支馈线故障状态；④type4，主馈线故障状态。对各系统状态进行类型判断，对应解列后形成的微电网级孤岛和主馈线级孤岛两类孤岛系统，如图1所示。

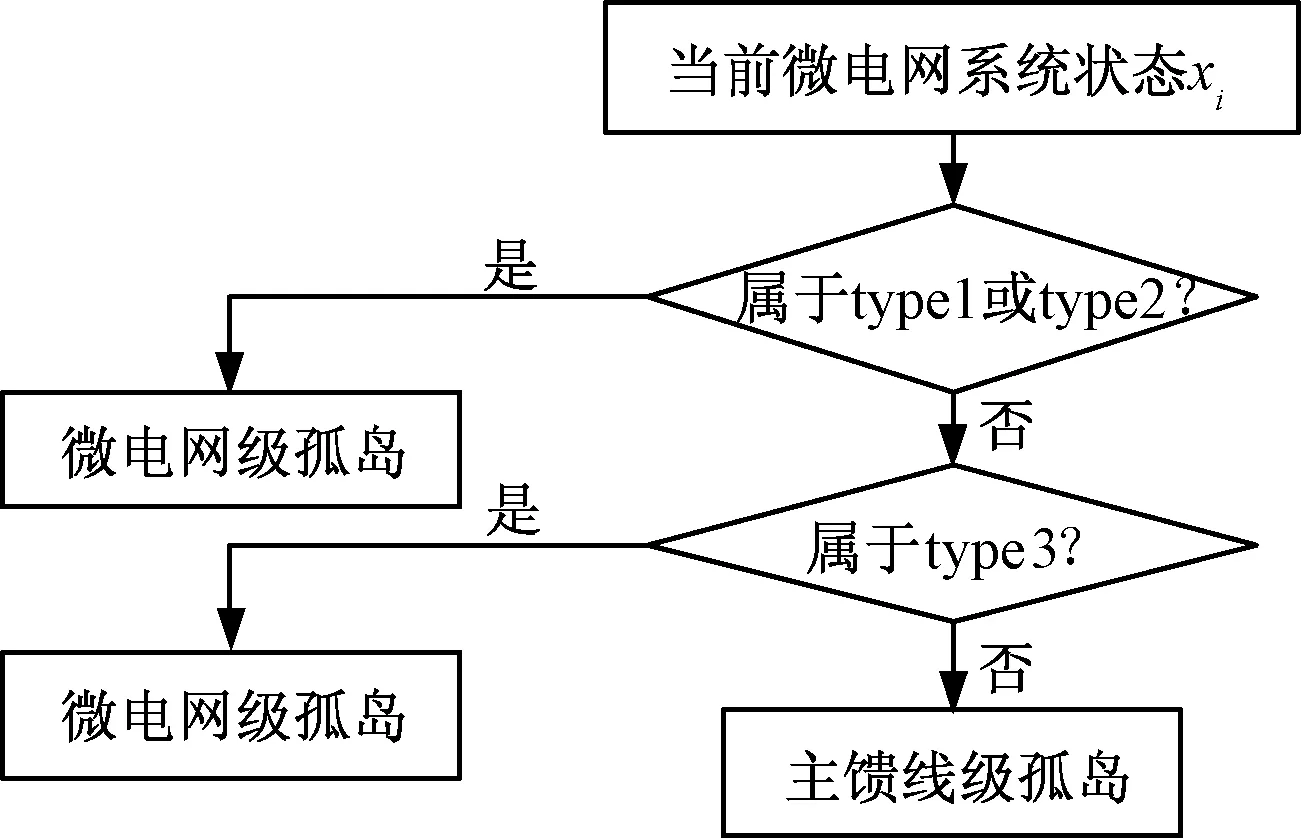
图1 孤岛类型判断示意图Fig.1 Island type discrimination diagram

微电网中储能装置的主要作用为功率缺额时作为可控电源出力，计及储能装置最大输出功率及最大容量，建立储能装置充放电模型。

(11)

式中，Pch(t)、Pdisch(t)为储能装置实时充、放电功率；Pch,max、Pdisch,max为设定的最大充、放电功率；PDG,i(t)为孤岛系统内第i个DG装置的实时有功出力；PL,j为孤岛系统内第j个负荷的有功功率。

(12)

式中，Qin、Qout为储能装置充电量、放电量；Qremain为储能装置剩余电量；Qmax、Qmin为储能装置最大、最小容量限度。

考虑储能装置充放电作用下的故障解列后孤岛系统也可能需切除部分负荷。采用考虑负荷重要度的切负荷策略，优先考虑重要负荷供电，仅考虑有功功率充裕性下，对非重要负荷按照最小负荷点优先切除原则，逐步判断切负荷的情况。则故障解列后孤岛系统的非重要负荷切负荷策略判定式为：

(13)

先假定解列后孤岛系统内所有非重要负荷点均不被切除，判断是否满足式(13)，若否，孤岛内有功功率最小的非重要负荷点优先被切除，直到满足式(13)为止。

4.2 静态安全约束

孤岛运行微电网主要有主从控制、对等控制和综合控制3种策略。孤岛运行微电网采用对等控制或综合控制策略时，系统没有平衡节点，由采用下垂控制DG装置调节微电网的频率和电压，系统稳态频率是未知状态变量，而频率对电力系统影响很大，严重时会造成系统的瓦解。因此，孤岛运行微电网短期可靠性评估中需要考虑的静态安全约束包括节点电压幅值约束和稳态频率约束。

节点电压幅值安全性约束为：

Ui,min≤Ui≤Ui,max

(14)

式中，Ui,max、Ui,min为设定的节点i电压幅值上、下限，分别取为1.05pu、0.95pu。

稳态频率安全性约束为：

fmin≤f≤fmax

(15)

式中，fmax、fmin为设定的稳态频率上、下限值，分别取为1.004pu、0.996pu。

主从控制的孤岛微电网系统有平衡节点，系统稳态频率为定值，且一般为工频，此情况下不需考虑稳态频率安全性约束。采用文献[20]中的潮流计算方法对切负荷后的孤岛系统进行确定性潮流计算，得到系统的稳态频率和节点电压值，如果其不满足式(14)和式(15)的约束，则切除相应的负荷。

4.3 短期可靠性指标及评估流程

电力系统可靠性水平是通过可靠性指标来度量的。本文定义3个孤岛运行微电网短期可靠性指标：系统切负荷概率(system Loss of Load Probability,LOLPS)、系统电量不足期望值(system Expected Energy Deficient Supplied,EEDSS)、负荷点平均停电时间(Load Average Interruption Duration,LAID)。

(16)

(17)

(18)

式中，Si为第i个计及DG装置和储能装置出力的微电网系统整体状态；M为微电网孤岛运行时间T内的微电网系统整体状态的总状态数；di为状态Si的持续时间；fLOLP(Si)、fEEDS(Si)、fLAID,j(Si)的定义为：

(19)

(20)

(21)

式中，Pcut为切除负荷的功率。

采用系统短期时序状态转移抽样法，获得微电网时序系统状态，并考虑计划解列、孤岛系统切负荷策略、静态安全约束进行孤岛运行微电网短期可靠性评估，其主要步骤如下：

(1)输入微电网系统线路、负荷点、DG装置、储能装置参数，系统解列点及进入孤岛运行模式的初始时刻t0；设定孤岛运行时间T、方差系数q、抽样间隔Δt；令初始仿真次数l=0。

(2)采用系统短期时序状态转移抽样法，以Δt为间隔，抽取孤岛运行时间T内的微电网系统状态；令l=l+1。

(3)依次选取第l次仿真的每个系统状态xi，由图1判断各系统状态类型，得到各状态解列后所属的孤岛类型，对应形成其孤岛系统的拓扑结构；再根据所建立的考虑控制策略的DG装置出力模型，得到各时刻的出力信息；进而得到M个微电网系统整体状态。

(4)对第l次仿真的M个微电网系统整体状态的可靠性评估：首先采用计及负荷重要度的最小切负荷策略进行故障解列后孤岛系统的切负荷运算；再对切负荷后的孤岛系统进行潮流计算，切除不满足静态安全约束的负荷点；最后，由定义的短期可靠性指标式(16)～式(18)，计算出短期可靠性指标值。

(5)如果EEDSS指标的方差系数小于q，则计算l次可靠性指标的平均值，仿真结束；否则，返回步骤(2)。

5 算例分析

5.1 算例系统设置

取Benchmark 0.4kV低压微电网网架结构[21]，在节点1、6、17接入MT装置，节点8、13接入WT装置，节点12接入PV装置，节点15接入储能装置，节点2～5、7、10～12、14～16接入负荷点LP1～LP11，其中，LP3设为重要负荷；开关S1为微电网级孤岛解列点，开关S2为主馈线级孤岛解列点，构成的孤岛运行微电网如图2所示。系统基准功率取为100 kV·A，设主馈线和分支馈线长度分别为0.9km和0.6km，元件故障率、负荷点参数见文献[17]。

图2 孤岛运行微电网算例系统Fig.2 Topology of islanded microgrid example system

设WT装置1、WT装置2的额定功率分别为(0.1+j0.06)pu、(0.2+j0.12)pu，切入风速vci、额定风速vr、切出风速vco分别为3m/s、15m/s和25m/s。PV装置的光电转换效率ηC=0.1，阈值常数KC=200W/m2。储能装置Pch,max、Pdisch,max均为(0.2+j0.12)pu，Qmax=120kW·h，Qremain初值为Qmax。设微电网算例系统进入孤岛运行模式的初始时刻t0=0，孤岛运行1个星期(168h)。设定初始时刻微电网内所有元件处于正常工作状态，系统短期时序状态转移抽样法抽样的方差系数q=0.01。

5.2 算例系统的短期可靠性评估结果

(1)系统短期时序状态转移抽样法的验证

取系统中只含有一个MT装置1，设其在t=0时刻的状态概率分布P(0)=[1,0]，分别采用解析法式(5)、本文提出的系统短期时序状态转移抽样法得到其1个星期内的平均不可用率值，结果如表1所示，其中以解析法得到的值作为真值。

表1 不同计算方法下得到的元件平均不可用率比较Tab.1 Comparison of components average unavailability under different computing methods

由表1可知，本文提出的系统短期时序状态转移抽样法得到的平均不可用率与真值的差值小，验证了本文抽样方法的正确性。

(2)取总仿真次数N=105次，分别取Δt=1h、Δt=2h和Δt=3h，采用本文提出的系统短期时序状态转移抽样法对微电网算例系统状态进行抽样，得到系统故障状态x1～x23出现的次数，结果如图3所示。

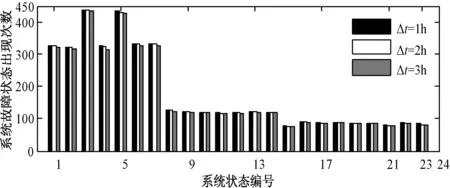
图3 不同抽样间隔下得到的系统故障状态数Fig.3 Number of system failures under different sampling intervals

由图3可知，随着抽样间隔Δt的增大，抽样得到的系统故障状态数越来越少。Δt=2h与Δt=1h下得到的系统故障状态数的差值不大，最大相对误差为1.12%，在可接受的范围内；而Δt=3h与Δt=1h下得到的系统故障状态数的差值较大，因此，确定本文算例系统的Δt取值为2h，同时表明本文提出的系统短期时序状态转移抽样法在保证一定精度的前提下，可通过增大抽样间隔来提高抽样效率。

(3)设孤岛运行微电网算例系统采用主从控制策略，DG配置方案为：MT装置1为恒压恒频控制，其最大出力为(0.3+j0.225)pu；MT装置2、MT装置3为恒功率控制，给定的注入功率分别为 (0.3+j0.18)pu、(0.4+j0.25)pu；WT装置1、WT装置2、PV装置为恒功率控制，采用本文所提方法对其进行短期可靠性评估，得到24h的可靠性评估结果，如图4所示。168h的可靠性评估结果如图5所示。

图4 24h的短期可靠性评估结果Fig.4 Short-term reliability evaluation results in 24h

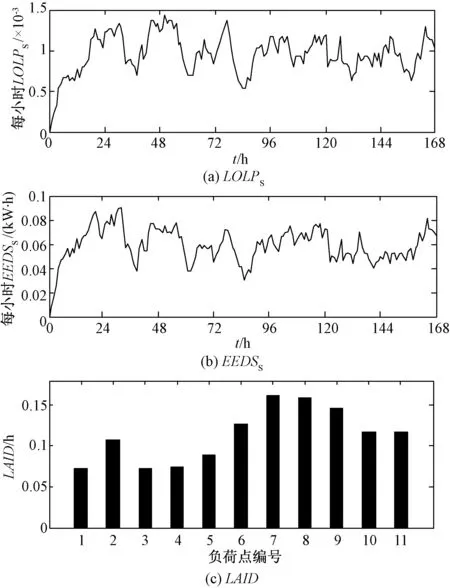
图5 168h的短期可靠性评估结果Fig.5 Short-term reliability evaluation results in 168h

评估结果分析如下：

(1)由图4可知，t∈(0,24]h时，孤岛运行微电网算例系统的短期可靠性中，白天的LOLPS、EEDSS值较低，夜晚的LOLPS、EEDSS值较高，原因如下：微电网孤岛运行初期，储能装置中的剩余电量较充足，随着时间的推移，储能装置中的剩余电量被不断消耗，且PV装置出力与光照总辐射量有关，而夜晚的光照总辐射量为0，PV装置出力为0，导致短期可靠性指标LOLPS、EEDSS值逐渐增加，系统可靠性水平逐渐降低。仿真结果符合理论分析，表明了本文提出的孤岛运行微电网短期可靠性评估方法的正确性和有效性。

(2)由图4和图5可知，孤岛运行微电网的短期可靠性指标值随时间变化，但并不是单调变化，这是由于孤岛运行微电网的短期可靠性水平不仅与系统时序状态有关，且与DG装置出力的变化有关，仿真结果符合理论分析。

5.3 微电网控制策略对短期可靠性的影响

设孤岛运行微电网算例系统采用综合控制策略，MT装置1、MT装置2、MT装置3采用P-f/Q-U下垂控制，其额定功率分别取为(0.3+j0.225)pu、(0.3+j0.18)pu、(0.4+j0.25)pu，WT装置1、WT装置2、PV装置为恒功率控制，采用本文所提方法对其进行短期可靠性评估，得到的负荷点平均停电时间指标值如图6所示。LOLPS、EEDSS指标与5.2节采用主从控制策略的孤岛运行微电网的LOLPS、EEDSS进行比较，结果如表2所示。

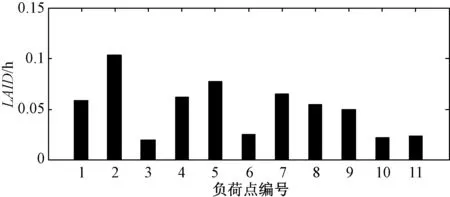
图6 综合控制策略下的负荷点平均停电时间Fig.6 LAID under comprehensive control

主从控制策略综合控制策略LOLPS96741×10-48451×10-4EEDSS/(kW·h)9973550254

由表2、图5(c)和图6可知，在相同的DG装置和储能装置容量配置下，孤岛运行微电网算例系统采用综合控制策略下的短期可靠性指标LOLPS、EEDSS值比采用主从控制策略下的值小，即短期可靠性水平要高，这是由于主从控制策略的孤岛运行微电网由恒压恒频控制的主控DG装置支撑系统的频率和电压，一旦出现主控DG装置故障，将会导致全网停电；而采用综合控制策略的孤岛运行微电网由下垂控制的DG装置共同调节系统的频率和电压，只要故障解列后的微电网系统中存在下垂控制的DG装置，即可满足部分负荷的供需平衡，避免了全网停电，因此孤岛运行微电网采用综合控制策略时的短期可靠性水平比采用主从控制策略下高。此外，采用考虑负荷重要度的切负荷策略，重要负荷LP3的可靠性为较高水平。

5.4 静态安全约束对短期可靠性的影响

取5.2节采用主从控制的孤岛运行微电网和5.3节采用综合控制的孤岛运行微电网算例配置，设置两种评估方案：①考虑静态安全约束；②不考虑静态安全约束。取t=12h时的LOLPS指标作为比较对象，评估结果如表3所示。

由表3可知，考虑静态安全约束下，采用主从控制和综合控制策略的孤岛运行微电网LOLPS指标均增大。其中，采用主从控制的孤岛运行微电网LOLPS指标增大幅度较小，这是因为采用主从控制策略的孤岛运行微电网有平衡节点，其频率为定值，只需考虑节点电压幅值的约束；采用综合控制策略的孤岛运行微电网LOLPS指标增大幅度较大，这是因为采用综合控制策略的孤岛运行微电网无平衡节点，节点电压幅值和系统频率均影响微电网短期可靠性。

表3 有无考虑静态安全约束的短期可靠性指标比较Tab.3 Comparison of short-term reliability indices with or without static safety constraints

6 结论

针对孤岛运行微电网短期可靠性评估的特点，本文提出了一种孤岛运行微电网短期可靠性评估的模拟法，算例结果及分析表明：

(1)系统短期时序状态转移抽样法可得到系统的短期时序状态，进而得到具有时序性的系统可靠性指标值，且该方法属于模拟法，可得到负荷点平均停电时间等重要的可靠性指标值，适用于孤岛运行微电网系统的短期可靠性评估。

(2)采用不同控制策略的孤岛运行微电网的短期可靠性水平不同，采用综合控制策略较采用主从控制策略的孤岛运行微电网的短期可靠性水平高。

(3)考虑故障解列、孤岛系统切负荷及静态安全约束的孤岛运行微电网短期可靠性评估，能更准确地反映孤岛运行微电网的实际短期可靠性水平。

[1] 杜少飞，谢文超，朱永强，等(Du Shaofei, Xie Wenchao, Zhu Yongqiang, et al.).并网型直流微电网主动协调控制方法研究(Research on active coordination control method for grid-connected DC microgrid)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2017，36(6)：30-38.

[2] 蔡冰倩，贾利虎，朱永强，等(Cai Bingqian, Jia Lihu, Zhu Yongqiang, et al.).直流微电网电压等级序列选择的影响因素研究(Research on influence factor of voltage class series option in DC microgrid)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(12)：45-51.

[3] 王成山，武震，李鹏(Wang Chengshan, Wu Zhen, Li Peng).微电网关键技术研究(Research on key technologies of microgrid)[J].电工技术学报(Transactions of China Electrotechnical Society)，2014, 29(2)：1-12.

[4] 杨新法， 苏剑，吕志鹏，等(Yang Xinfa, Su Jian, Lv Zhipeng, et al．)．微电网技术综述(Overview on microgrid technology)[J]．中国电机工程学报(Proceedings of the CSEE)，2014, 34(1)：57-70．

[5] 鲁宗相， 王彩霞，闵勇，等(Lu Zongxiang，Wang Caixia，Min Yong， et al．)．微电网研究综述(Overview on microgrid research)[J]．电力系统自动化(Automation of Electric Power Systems)，2007，31(19)：100-107．

[6] 孙元章，程林，何剑(Sun Yuanzhang, Cheng Lin, He Jian).电力系统运行可靠性理论(Power system operational reliability theory)[M].北京：清华大学出版社(Beijing: Tsinghua University Press)，2012.

[7] Liu H, Sun Y, Cheng L, et al. Online short-term reliability evaluation using a fast sorting technique[J]. IET Generation Transmission & Distribution, 2008, 2(1): 139-148.

[8] Mccalley J, Asgarpoor S, Bertling L, et al. Probabilistic security assessment for power system operations[A]. 2004 IEEE Power Engineering Society General Meeting[C]. 2004. 212-220.

[9] Bie Z, Zhang P, Li G, et al. Reliability evaluation of active distribution systems including microgrids[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2342-2350.

[10] 王杨，万凌云，胡博，等(Wang Yang, Wan Lingyun, Hu Bo, et al.).基于孤岛运行特性的微电网可靠性分析(Isolated island operating characteristics based analysis on reliability of microgrid)[J].电网技术(Power System Technology)，2014，38(9)：2379-2385.

[11] 王杨，谢开贵，胡博，等(Wang Yang, Xie Kaigui, Hu Bo, et al.).基于时序模拟的离网型微网可靠性分析(Reliability analysis of islanded microgrid based on sequential simulation)[J].电工技术学报(Transactions of China Electrotechnical Society)，2016，31(6)：206-211.

[12] 刘明君， 李文沅，王财胜(Liu Mingjun，Li Wenyuan，Wang Caisheng)．孤岛模式运行下含潮汐发电和电池储能的微电网可靠性评估(Reliability evaluation for islanded microgrid with tidal power generation and battery energy storage system)[J]．电力自动化设备(Electric Power Automation Equipment)，2016，36(11)：33-39．

[13]Xu X，Mitra J，Wang T， et al． An evaluation strategy for microgrid reliability considering the effects of protection system[J]．IEEE Transactions on Power Delivery，2016，31(5)：1989-1997．

[14] 彭寒梅，曹一家，黄小庆，等(Peng Hanmei, Cao Yijia, Huang Xiaoqing, et al.).基于时变通用生成函数的孤岛运行模式下微电网可靠性评估(Reliability evaluation of microgrid in islanded operation mode based on TVUGF)[J].电力系统自动化(Automation of Electric Power Systems)，2015, 39(10)：28-35.

[15] 杨毅，雷霞，叶涛，等(Yang Yi, Lei Xia, Ye Tao, et al.).考虑安全性与可靠性的微电网电能优化调度(Microgrid energy optimal dispatch considering the security and reliability)[J].中国电机工程学报(Proceedings of the CSEE)，2014, 34(19)：3080-3088.

[16] 朱泽磊，周京阳，潘毅，等(Zhu Zelei, Zhou Jingyang, Pan Yi, et al.).考虑电力电量平衡的安全约束经济调度(Security constrained economic dispatch considering balance of electric power and energy)[J].中国电机工程学报(Proceedings of the CSEE)，2013，33(10)：168-176.

[17] 彭寒梅，曹一家，黄小庆(Peng Hanmei, Cao Yijia, Huang Xiaoqing).对等控制孤岛微电网的静态安全风险评估(Static security risk assessment of islanded microgrids under peer-peer control)[J].中国电机工程学报(Proceedings of the CSEE)，2016，36(18)：4837-4846.

[18] 梁惠施，程林，刘思革(Liang Huishi, Cheng Lin, Liu Sige).基于蒙特卡罗模拟的含微网配电网可靠性评估(Monte Carlo simulation based reliability evaluation of distribution system containing microgrids)[J].电网技术(Power System Technology)，2011，35(10)：76-81.

[19] 杨锡运，孙宝君，张新房，等(Yang Xiyun, Sun Baojun， Zhang Xinfang, et al.).基于相似数据的支持向量机短期风速预测仿真研究(Short-term wind speed forecasting based on support vector machine with similar data)[J].中国电机工程学报(Proceedings of the CSEE)，2012，32(4)：35-41.

[20] 彭寒梅，曹一家，黄小庆(Peng Hanmei, Cao Yijia, Huang Xiaoqing).基于BFGS信赖域算法的孤岛微电网潮流计算(Power flow calculation of islanded microgrids based on BFGS trust region method)[J].中国电机工程学报(Proceedings of the CSEE)，2014, 34(16)：2629-2638.

[21] Rudion K, Styczynski Z A, Hatziargyriou N, et al. Development of benchmarks for low and medium voltage distribution networks with high penetration of dispersed generation[A]. 3rd International Symposium on Modern Electric Power Systems[C]. 2006. 115-121.