基于萤火虫算法的TCIPC功率振荡阻尼控制器的设计

李 娟， 王文英

(东北电力大学电气工程学院， 吉林省 吉林市 132012)

1 引言

随着科学技术的日益飞跃和国民经济的不断提高，大系统容量、高电压等级、电网跨区域互联，系统市场化运营已经成为了现代电力系统的主要特点。受跨区域电网结构日趋复杂，功率传输量逐渐增长的影响，电力系统安全运行的暂态和动态稳定的重要性日益增加。最近开发的灵活交流输电系统(Flexible AC Transmission System, FACTS)技术可以快速改变网络结构和控制器参数，提高现有网络的利用率，并且通过灵活控制有功和无功功率，增强输电线路传输能力，显著提高系统暂态和动态稳定性[1,2]。

相间功率控制器(Interphase Power Controller, IPC)被电力工作者认为是当前最适合开发应用的FACTS设备之一[3,4]，其通过等效改变线路的电抗、移相角等参数可对线路传输的有功和无功功率进行控制，具有鲁棒潮流控制、限制短路电流和电压解耦等的优良特性[5,6]。传统的IPC对参数的调整方法是操作机械开关投切电感器、电容器的组数，以此改变电感、电容元件参数的大小，从而控制联络线上的潮流分布。但由于机械式开关的延时性，很难实现IPC对系统进行连续、快速的控制。IPC连接的两电网联络线受端发生短路故障时，如果不及时采取措施进行有效地控制，可能引起系统功率振荡，不利于系统稳定运行。

本文详细分析了可控相间功率控制器(TCIPC)的基本工作原理，通过调节晶闸管控制TCR支路感抗和晶闸管串联电容器TCSC支路容抗灵活地控制联络线的传输功率，并且在研究TCSC控制模型的基础上，设计了基于TCIPC的附加阻尼控制器，采用全局优化方法(萤火虫算法)和局部优化方法(模式搜索算法)相结合的方式优化阻尼控制器的关键参数，以达到阻尼系统功率振荡、提高系统稳定性的目的。最后通过算例仿真进行验证。

2 可控相间功率控制器的基本结构原理

2.1 TCIPC的基本结构

TCIPC将IPC的电感和电容支路分别由晶闸管进行触发控制。其中两个反并联的晶闸管与电感支路串联，通过连续调节晶闸管的触发延迟角α，相当于改变电感支路的等效感抗值；电容支路由TCSC的容性微调模式来代替传统静止IPC中的电容器实现电容支路的参数调节[7]。其基本结构如图1所示。在单机无穷大系统的输电线中间安装TCIPC，并经双回输电线与无穷大母线侧相联。

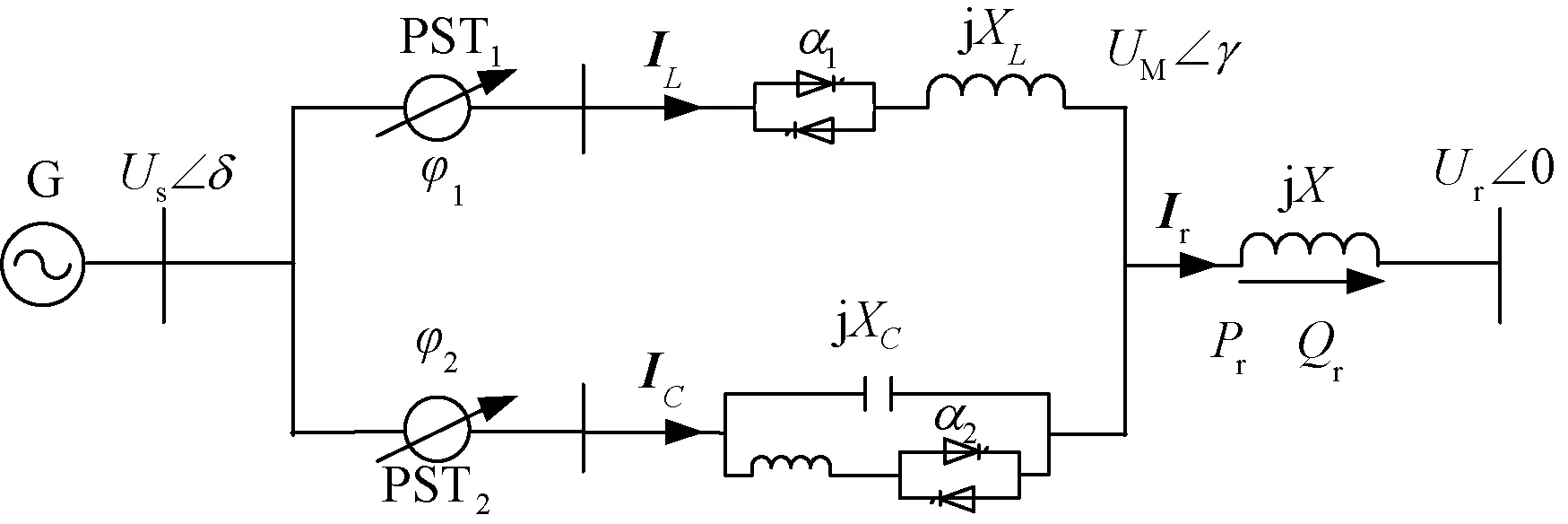
图1 安装TCIPC装置的单机无穷大系统Fig.1 Single machine infinite bus system with TCIPC device

TCIPC电感支路的晶闸管触发角与电抗的关系：

(1)

式中，0≤α1≤π/2；XL=ωL。

构成TCIPC电容支路的TCSC基本结构是由TCR与固定的静止电容并联而成，通过控制TCR中晶闸管的触发角α2来改变其电抗值，进而获得连续可控的串联电容值。

电容支路电抗的数学模型可以表示为：

(2)

式中，XC=1/(ωC)。

2.2 TCIPC的功率控制机理

相间功率控制器具有增强线路潮流的可控性和限制短路电流等特性，所以将其应用于电网互联具有一定的作用，同时对系统运行的稳定性也具有一定的影响。

由图1，可得流经双回输电线的电流与输电线两端的电压之间的关系表达式为：

(3)

由TCIPC出口流经联络线的电流Ir又可表示为：

(4)

联立式(3)、式(4)，求解方程组，可得TCIPC出口处电压UM为：

(5)

经由TCIPC流入无穷大系统的有功功率为：

(6)

式中，XL(α1)为可调节感抗；XC(α2)为可调节容抗。选择调谐型IPC，则XL(α1)=XC(α2)=XIPC。

由式(3)～式(6)可见，在TCIPC两个支路移相角的值固定的情况下，通过控制晶闸管触发角等效地控制TCIPC电感支路的感抗和电容支路的容抗，可以调节发电机向系统传输功率的能力，提高功率传输极限。如果系统发生短路故障时，发电机向系统传输功率的能力能够得到提高，系统阻尼功率振荡的能力将会提高[1]。

3 TCIPC阻尼系统功率振荡的机理分析

图1中，假定发电机暂态电势和机械功率恒定，由式(3)和式(4)，不计线路与装置的电磁暂态过程，可得具有调谐型IPC的单机向无穷大系统输送电磁功率的表达式：

(7)

由于经典的相间功率控制器如IPC120、IPC240等其移相控制角分别为60°、-60°和120°、-120°，电感和电容支路的移相角度正好相反，因此，可以令φ1=φ2=φ，则式(7)可变为：

(8)

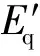
含有TCIPC的单机无穷大系统的转子运动方程可用如下非线性状态方程表示：

(9)

式中，Pe为发电机电磁功率；Pm为机械功率；δ为发电机转子运行角；ω为转子角速度；ω0为同步转速；H为转动惯量；D为阻尼系数。

当系统中不含TCIPC时，有

式中

将Pe在δ0处按泰勒级数展开，略去Δδ的二次项和高次项得系统微分方程为：

(10)

由式(10)求得其特征值λ为：

(11)

从式(11)可以看出，当cosδ0>0时，由于忽略发电机本身的阻尼，系统为等幅振荡模式。若要避免系统发生振荡，需要加入额外的调节功率，假设加入的调节功率为：ΔP=k1Δδ+k2Δω，微分方程变为：

(12)

由式(12)求得其特征值为：

(13)

令

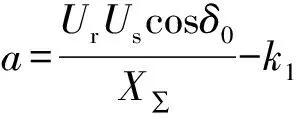
由式(13)可以看出,若k2<0，当a<0时，λ出现一正的实根；若k2>0，当a>0且b>0或b<0时，λ实部均出现正值。

上述两种情况下，系统均会出现非周期振荡，表明系统阻尼转矩仍不足以满足稳定运行的需求。为了增加系统阻尼，加入TCIPC,假设XIPC随着Δω的变化而进行调整，且令XIPC=-kΔω+x(k>0)，对式(8)中Pe进行泰勒级数展开，可求得特征值为：

(14)

由式(14)可以看出，对于IPC120、IPC240均有sinφ>0，λ的实部始终为负，系统是稳定的。这说明加入TCIPC能够实现阻尼系统功率振荡的目的，即当Δω增大时，XΣ减小，式(14)实部的绝对值增大，增强了系统的阻尼效果。

4 TCIPC阻尼控制器模型与设计

TCIPC对电力系统控制所具有的潜力是基于其电感、电容支路的快速调节阻抗能力，阻抗控制的优劣影响着整个控制系统的响应速度与稳定性[8]。本文对电容支路即TCSC进行控制调节，并使电感支路始终保持共轭。

阻尼控制器的基本原理是通过TCSC的阻抗参考值Xref与调制信号ΔX的叠加，进而改变TCSC的实际输出阻抗，以阻尼功率振荡。为了使线路的功率振荡得到抑制，将两级超前滞后结构加入附加阻尼控制环节以产生纯阻尼，选用的传递函数为：

式中，Ks为增益模块；1/(1+sT0)为输入信号的测量环节；sTw/(1+sTw)为滤波器；Tw为滤波器的时间常数，其值通常在1～20s之间变化。

相位补偿模块提供适当的相位超前特性来补偿输入和输出相位之间的相位滞后，每个超前-滞后补偿环节最多可实现60°的相位补偿。阻尼控制器模型如图2所示。

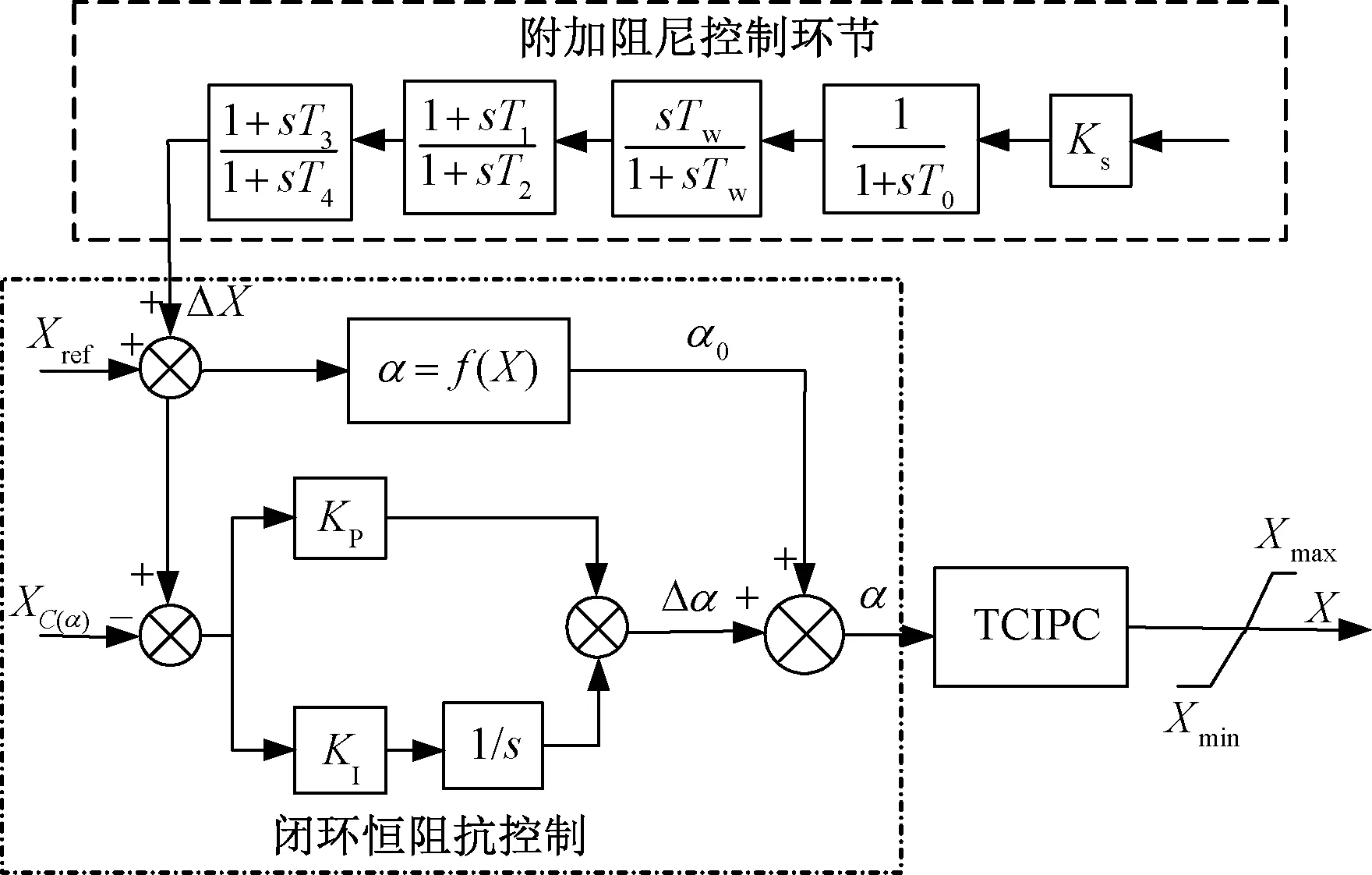
图2 IPC附加阻尼控制器控制模型Fig.2 IPC additional damping controller control model

4.1 控制器输入信号的选择

在电力系统发生扰动时，输入信号必须给出正确的控制信号。控制器的输入信号可以采用本地信号，如本地线路的电流、有功功率、母线电压等；也可以采用远程信号，如发电机转子角速度差、其他母线间的相位偏差以及临近线路的有功功率等[9,10]。为了避免额外的通信成本，提高可靠性，输入信号应优先选择本地可测量的。然而，本地的控制信号虽然容易获得，但是可能不包含所需的振荡模式，并且没有高度的可控性和可观性。因此，远程信号中发电机转子角速度作为输入信号，是该阻尼控制器更好的选择。远程信号由于信号传输，会有时间延迟，有文献表明，最坏的情况下会有50ms的延迟，这可能会影响控制器的可靠性[11,12]。为了利用远程信号的同时，避免它的缺点，本文采用由本地可测量的有功功率信号改进的远程速度偏差信号作为控制器的输入信号。

有功功率和角速度的关系为：

(15)

式中，M为惯性时间常数。M和D被假定为可调参数。因此，转子角速度可以表示为：

(16)

图3为输入信号的方框图。图3中的Δω为速度偏差信号，送入图2中的超前滞后结构的TCIPC附加阻尼控制器中。

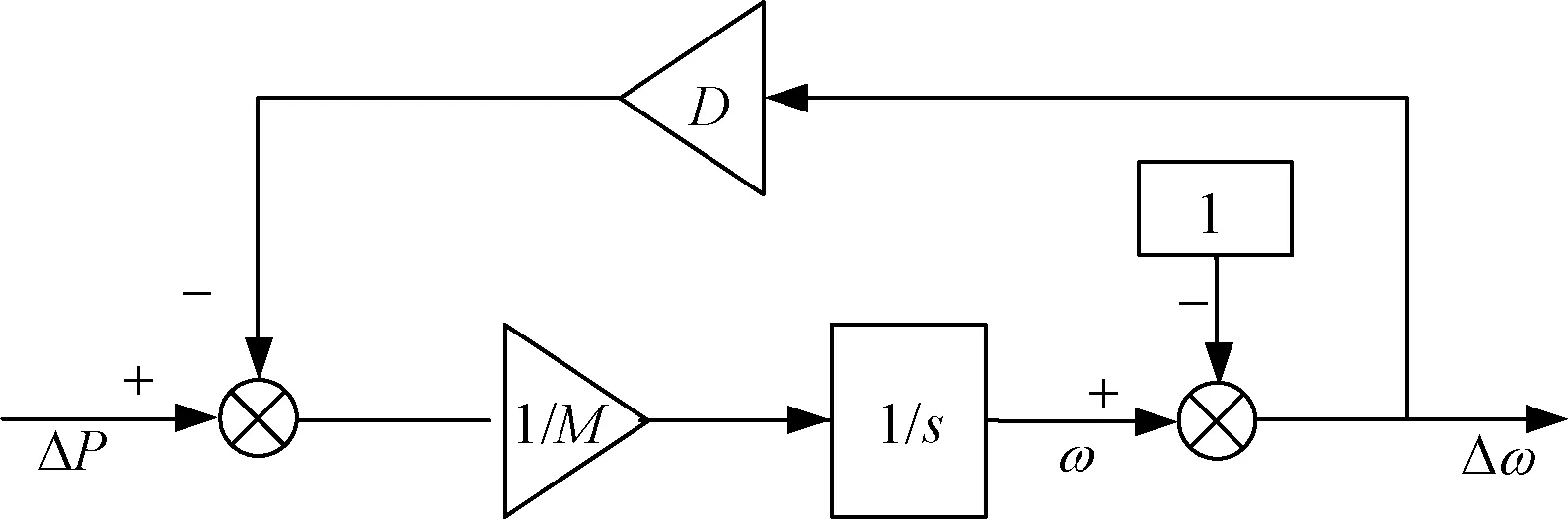
图3 输入信号的方框图Fig.3 Block diagram of input signal

为了利用萤火虫算法优化阻尼控制器参数，须列写含有TCIPC控制器的系统扩展方程，具体为：

(17)

式中，X1、X2、X3为新增的状态变量。TCIPC的输入为Δω，输出为ΔX。

在超前滞后结构控制器中，滤波器时间常数Tw和超前滞后环节时间常数T2、T4通常可取经验值，而控制器的增益Ks和时间常数T1、T3为待优化参数。

4.2 控制器设计问题的转化

电力系统受到大扰动后，TCIPC阻尼控制器可以最大限度地减少系统振荡，以达到提高系统稳定性的目的。电力系统振荡的发生是由于扰动后输入机械功率和电磁功率之间产生差额，造成发电机转子角速度变化，功率差额量越大，发电机的转速变化越大，因此，转子的速度偏差最小化可以作为控制器优化目标，目标函数方程为：

(18)

式中，t为仿真的时间范围。从动态的角度看，对转速偏差绝对值与时间的乘积进行积分时，能够兼顾受扰动时系统在振荡过程中和趋于平稳时的输出误差。为求取目标函数，对电力系统模型的时域仿真进行了周期性模拟，目的是最小化目标函数，以根据调节时间和超调量提高系统响应，实现控制器参数优化。问题的约束条件是TCIPC阻尼控制器的参数范围。因此，控制器的设计问题可以转化为如下优化问题的求解过程：

(1)目标函数为：

MinJ

(2)约束条件为：

Dmin≤D≤Dmax

Mmin≤M≤Mmax

Evaluation on the sensory efficacy of water glow sensation for skin 12 20

5 提出的优化技术

电力系统的大小和复杂性随着电力需求的增加而增长，这一性质决定优化过程中必须要在结合电力系统实时控制的技术和方法的基础上使用智能系统。最近，一种新的生物启发的元启发式算法——萤火虫算法(Firefly Algorithm, FA)被提出，并已成功应用于解决非线性和非凸优化问题。FA简单、灵活、多功能，它在解决复杂多变的工程实际问题中非常有效。

FA作为一种全局优化方法，其目的是搜索一个寻优空间，单独使用易陷入局部极小且进化后期收敛速度慢，致使求解精度不高。而模式搜索(patternsearch, PS)是一种局部优化方法，其目的是应用于局部地区，但其通常不善于搜索广泛地区，且搜索结果的好坏在一定程度上取决于初始点的选取，若初始点选取不合适，易使结果陷入局部极小，因此不适用于单独的全局优化。为了克服FA的弱局部搜索能力和PS的初值敏感性，优化问题尝试使用混合的萤火虫算法和模式搜索技术(hybrid Firefly Algorithm and Pattern Search，h-FAPS)。

5.1 萤火虫算法原理

萤火虫算法是群集智能优化算法领域的最新算法，由剑桥学者Yang Xin-she等在2008年提出，源于模拟自然界萤火虫晚间利用发光行为与同伴进行觅食、求偶等信息交流的自然现象[13]。该算法将解空间的每个解看作一只萤火虫，萤火虫种群视作随机分布在搜索空间的初始解，解空间中每只萤火虫按照自然界萤火虫的运动规律进行移动。萤火虫经过每一代的移动，聚集到较优的萤火虫周围，由此实现种群寻优的目的。

(1)荧光素更新：将每只萤火虫i(Ksi，T1i，T3i)在t迭代的位置对应的目标函数式(18)转化为荧光素值li(t)：

li(t)=(1-ρ)li(t-1)+γJ(xi(t))

(19)

式中，γ为荧光素更新率；ρ∈(0,1)，为控制荧光素值的参数。

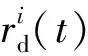
(20)

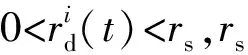
(21)

吸引度为：

β(r)=β0e-γr2

(22)

式中，β0为最大吸引度(r=0处)。

(3)位置更新：

(23)

式中，s为移动步长。

当两萤火虫之间距离很近(r→0)时，若γ→0,则β→β0，若取β0=1，位置更新公式变化为：

(24)

这意味着萤火虫所在的环境为理想环境，萤火虫发光在空中无任何衰减，任何萤火虫均可在所处范围内直接找到最优、最亮个体。

若γ→∞，则β→0，意味着萤火虫个体间的吸引度为零，发光对个体的移动距离和方向无任何影响和作用，单个个体移动几乎是随机或接近于随机的运动，失去了群体智能的特性。因此实际优化中，往往取γ∈[0.01,100]。

(4)动态决策域半径更新：

(25)

式中，α为感知半径变化系数；ni为感知范围内限定的优秀个体数。当感知范围内的较优个体数大于ni时，个体的邻域半径减小，反之则增大。

当荧光素值高于萤火虫i本身的相邻萤火虫j出现，且距离差在彼此的感知范围以内时，萤火虫i则以一定概率pij(t)选中邻居j，并向其移动，按式(22)更新位置，重新求取此处的目标函数值，并按式(19)进行荧光素值的更新。

5.2 模式搜索算法原理

模式搜索是由Hooke和Jeeves于1961年提出的一种直接局部搜索算法[14]。PS在某个初始点附近，根据选定模式形成新的点集，对初始点与新点集的函数值进行比较，把较小者确定为新的起点；并且模式自身按照本次迭代的成败，进行自适应调整[15]。算法流程如下：

(1)给定模式向量{Vi}，在初始点周围形成新的点集。

(2)按照模式向量集形成网格(mesh)。一般将PS算法进行每次搜索时不同位置的点在空间生成的网格阵列称为网格。

(3)对网格点进行投票(poll)。在当前迭代的基点xm与生成的点集xm+δm{Vi}中，选择最小点，作为下一次迭代的起点xm+1。如果本次迭代中得到一个比当前基点好的新点，就称作“投票成功”；反之则称“投票失败”。一般情况下，采用完全投票寻优时，结果相对精确，但需要的时间较长；而采用不完全投票时，虽然耗时短，但极有可能陷入局部最优。

(4)对扩张因子θe(>1)和收缩因子θc(<1)进行定义。投票成功时，扩大网格尺度δm+1=θeδm；失败时则缩小网格尺度δm+1=θcδm。在算法应用过程中，通常取θe∈[1,2]，θc∈[0.1,0.5]。

(5)定义精度ε(>0)，若|δm|<ε，停止迭代，输出当前最优值。

5.3 引入模式搜索算法优化的萤火虫算法

首先用萤火虫算法框架进行全局搜索，为模式搜索提供更精确的初值，并通过模式搜索算法实现进一步局部搜索，从而构建一种引入模式搜索算子的混合算法[16]。算法流程图如图4所示。

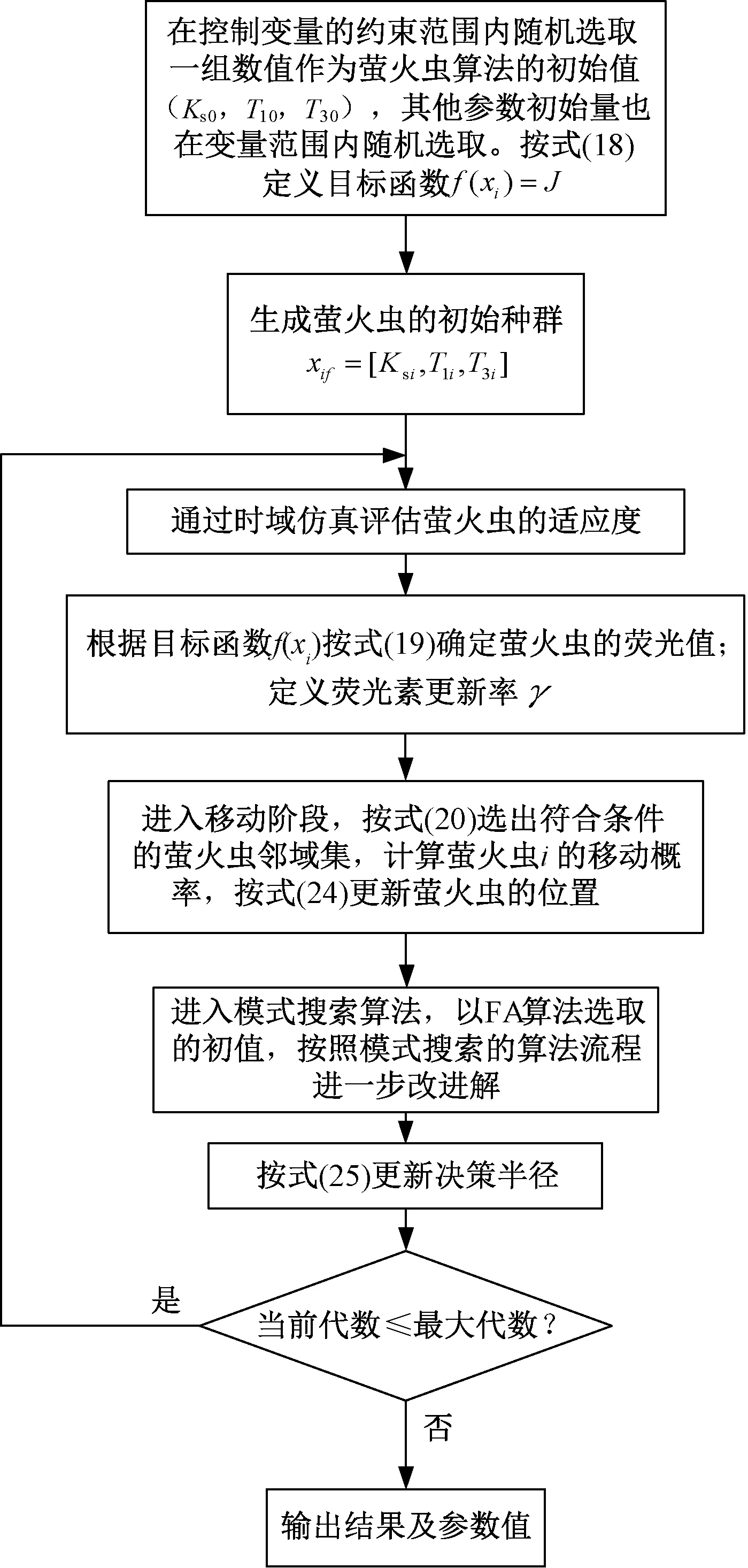
图4 h-FAPS技术流程图Fig.4 Flow chart of h-FAPS technology

6 算例仿真

本文应用Simulink搭建了装有调谐型TCIPC的单机无穷大系统模型，如图5所示。对基于萤火虫算法设计的TCIPC功率振荡阻尼控制器的有效性进行仿真验证。

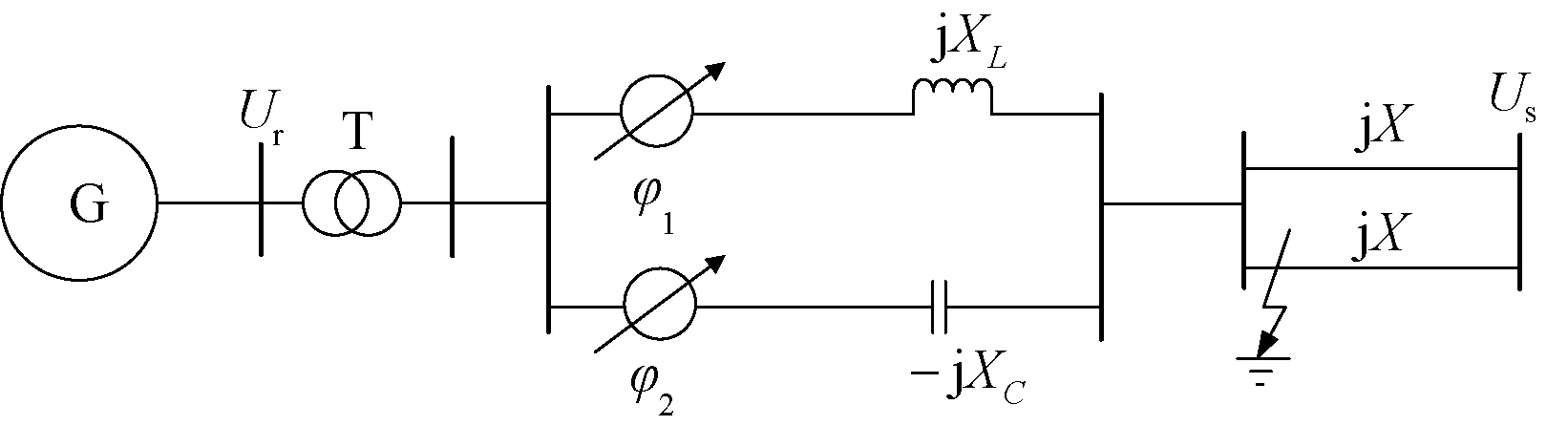
图5 安装TCIPC的单机无穷大系统图Fig.5 Single machine infinite system diagram with TCIPC

图5中，G为发电机，Ur为发电机机端电压，Us为无穷大系统母线电压。发电机容量为2100MV·A,变压器变比为13.8/500kV，线路等值电抗X=47Ω，H=3.7s，D=0(不考虑自身阻尼振荡)；TCIPC电感支路的感抗和电容支路容抗初始值为56.52Ω。

在系统的闭环恒阻抗控制中，Kp=0.5，Ki=16。超前滞后结构控制器中，给定的参数为Tw=10s，T2=0.05s，T4=0.05s，待定参数为Ks、T1、T3。参数优化过程中，采用h-FAPS算法，根据已有的研究结果[17-19]结合多次实验，算法参数设置如下：种群大小取为50，最大进化代数为100，初始荧光素的值l0为5，控制萤火虫邻居数目的邻域阈值ni为5，感知半径变化系数α为0.08，最大感知范围rs为5，控制荧光素值的参数ρ为0.4，荧光素更新率γ为0.6；移动的步长s为20，决策域范围为30；模式搜索的初始步长为0.01及加速因子为0.5。

(1)模拟系统在t=1s时，发电机励磁电压发生5%的扰动并且持续0.5s的情况。

图6为阻尼控制器优化前后小扰动下发电机转子角速度响应曲线以及联络线功率变化曲线。经受小干扰时，系统的稳定性发生改变，转子角速度发生变化。由图6(a)可以看出，阻尼控制器经萤火虫算法优化后，转子角速度的振幅以及振荡次数均有所减小，但是振荡趋于稳定所需时间差别不是很大。图6(b)表明联络线功率在扰动后采用萤火虫算法优化后的阻尼控制器进行调整，振荡次数、摆动幅度以及振荡趋于稳定的时间都有明显降低。

(2)模拟无穷大母线侧一回输电线路始端在t=1s时发生三相短路接地故障，0.1s后故障切除。

为了验证所提基于h-FAPS算法的阻尼控制器的控制效果，图7分别给出了没有增加阻尼控制、只增加阻尼控制器以及对控制器参数进行优化后的发电机功角振荡曲线、转子角速度响应曲线及联络线功率变化曲线的波形图。

图7(a)为故障后发电机的功角振荡曲线。仿真结果表明，故障发生后，系统只进行闭环恒阻抗控制而未增加阻尼控制环节时，发电机功角δ基本呈等幅振荡，且振荡幅度较大，系统不能维持稳定运行。增加了阻尼控制后，系统是稳定的，并且仅仅经过几个摇摆周期后就迅速达到了稳定。而经过h-FAPS算法对控制器参数进行优化后，发电机功角振荡幅值更小，能够更快地达到稳定运行状态。

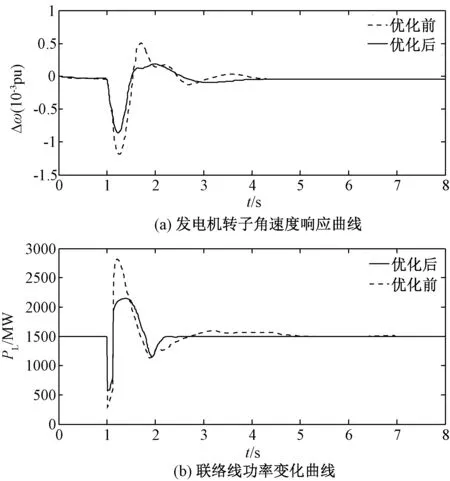
图6 小扰动下发电机转子角速度响应和联络线功率变化曲线Fig.6 Generator rotor angular velocity response curve and power change curve of tie line under small disturbance

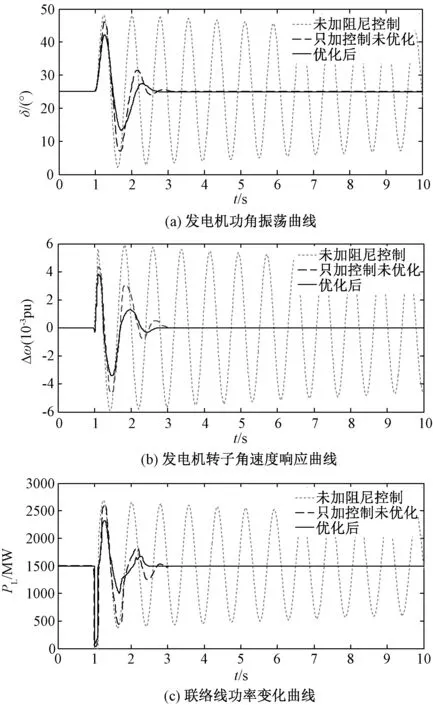
图7 不同方法下的仿真曲线Fig.7 Simulated curves with different algorithms

图7(b)为故障情况下转子角速度响应曲线。故障时，发电机机端电压会发生改变，进而影响系统稳定性。对仿真结果进行比较可以看出，增加阻尼控制器并对其参数进行优化后转子角速度的摆动幅度，振荡次数明显减少。

图7(c)为三相短路故障时联络线功率响应曲线。可以看出，对阻尼控制器参数进行优化后，联络线功率的振荡幅值明显减小，整个扰动过程显著缩短。可见，采用基于h-FAPS算法设计的TCIPC功率振荡阻尼控制器能够更加有效地提高系统对功率振荡的阻尼效果，使受到扰动后的系统迅速平稳地恢复稳定运行状态，提高系统的稳定性。

目标函数分别使用FA,h-FAPS以及遗传算法进行优化时的收敛性与迭代次数的关系如图8所示。可知，经过多次迭代以后，目标函数J达到最小且趋于稳定，并且h-FAPS比使用遗传算法以及单独使用FA进行优化时收敛速度快，优化效果好。

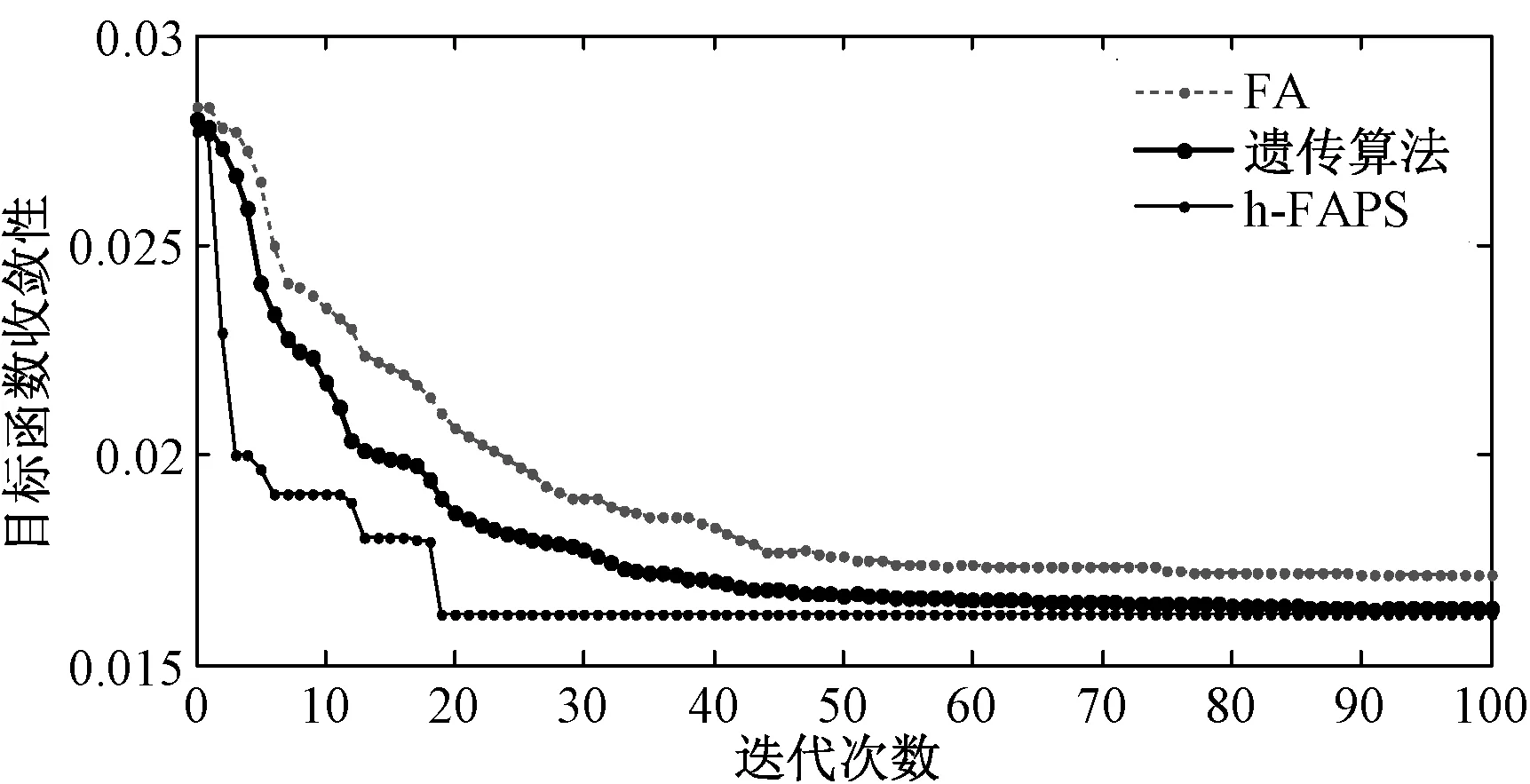
图8 目标函数的收敛性Fig.8 Convergence of objective function

7 结论

本文基于可控相间功率控制器的基本原理，分析了电感、电容支路对带TCIPC联络线传输功率的调节作用以及TCIPC阻尼系统功率振荡的机理,在此基础上设计了TCIPC功率振荡阻尼控制器。

综合萤火虫算法和模式搜索技术的优缺点，提出了一种混合的萤火虫算法和模式搜索技术，其能够应用于控制器的参数优化，并且基于此技术的TCIPC功率振荡阻尼控制器在系统发生大扰动后具有良好的控制作用。与单纯的闭环恒阻抗控制相比，可以降低功角、转速以及功率振荡的幅度，缩短振荡持续的时间，能够使得故障之后的系统迅速地恢复稳定运行状态，提高系统的稳定性。

[1] 李娟，严宇昕，聂鹏(Li Juan, Yan Yuxin, Nie Peng). 基于VSC的DCIPC阻尼系统功率振荡及限制短路电流的研究(Power oscillation damping and short circuit current limiting by VSC-based DCIPC)[J]. 电力自动化设备(Electric Power Automation Equipment)，2015，35(5)：58-63.

[2] Farmad M, Farhangi S, Afsharnia S. Application of voltage source converter in interphase power controller for power flow control and fault limitation[J]. IEEE Transactions on Power Delivery, 2008, 9(2): 2301-2306.

[3] 李娟，闫乃欣，周建颖，等(Li Juan, Yan Naixin, Zhou Jianying, et al.). TCIPC提高暂态稳定性的PI控制器设计(Designing PI controller in thyristor controlled interphase power controller for improving transient stability of power system)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2012，33(3)：68-71.

[4] 何大愚(He Dayu). 柔性交流输电技术及其控制器研制的新发展——TCPST, IPC(TCIPC)和SSSC(Facts technology and new process in the development of its controllers —TCPST, IPC (TCIPC) and SSSC)[J]. 电力系统自动化(Automation of Electric Power Systems)，1997，21(2)：1-6.

[5] 刘修宽，蒋维勇，纪延超，等(Liu Xiukuan, Jiang Weiyong, Ji Yanchao, et al.). 互联电网接入IPC参数调整时刻的研究(Research on the time to adjust IPC’s parameter in interconnected power system)[J]. 电机与控制学报(Electric Machines and Control)，2005，9(1)：64-67.

[6] Brochu J，Beauregard F，Lemay J，et al. Application of the interphase power controller technology for transmission line power flow control [J]．IEEE Transactions on Power Delivery, 1997,12(2): 888-894.

[7] 李娟，赵露，张冰冰，等(Li Juan, Zhao Lu, Zhang Bingbing, et al.). 基于参数协调的可控相间功率控制器调节特性研究(Adjustment characteristics of thyristor controlled interphase power controller based on parameter coordination)[J].电力自动化设备(Electric Power Automation Equipment)，2007，27(2)：16-19.

[8] 杨超(Yang Chao).可控串补(TCSC)控制方法的研究(Research on control method of thyristor controlled series compensator (TCSC))[D].南京：南京理工大学(Nanjing: Nanjing University of Science and Technology),2005.

[9] 林宇锋，徐政，黄莹(Lin Yufeng, Xu Zheng, Huang Ying). TCSC功率振荡阻尼控制器的设计(Design of TCSC auxiliary controller for inter-area power oscillation damping)[J].电网技术(Power System Technology), 2005，29(22)：35-39.

[10] Mahapatra S, Panda S,Swain S C. A hybrid firefly algorithm and pattern search technique for SSSC based power oscillation damping controller design[J].Ain Shams Engineering Journal,2014, 5(4):1177-1188.

[11] Panda G, Rautraya P K. Designing of SSSC-based damping controller using bacterial foraging algorithm to improve power system stability[J]. International Journal of Modelling, Identification and Control, 2014,21(2):172-183.

[12] Ali E S, Abd-Elazim S M. Optimal SSSC design for power systems via hybrid approach[J]. International Journal of Electrical Engineering, 2014, 14:138-147.

[13] Yang X S. Firefly algorithms for multimodal optimization[A].International Symposium on Stochastic Algorithms, SAGA 2009-Stochastic Algorithms: Foundations and Applications[C]. 2009. 169-178.

[14] Al-Othman A K, Ahmed N A, AlSharidah M E, et al.A hybrid real coded genetic algorithm - Pattern search approach for selective harmonic elimination of PWM AC/AC voltage controller[J].International Journal of Electrical Power & Energy Systems, 2013, 44(1):123-133.

[15] 张煜东，吴乐南，王水花(Zhang Yudong, Wu Lenan, Wang Shuihua). 基于遗传算法与模式搜索的混合优化算法(A hybrid optimization method based on genetic algorithm and pattern search)[J].南京信息工程大学学报(Journal of Nanjing University of Information Science and Technology)，2015，4(1)：34-39.

[16] 刘洪霞，周永权(Liu Hongxia, Zhou Yongquan).一种基于模式搜索算子的人工萤火虫优化算法(A glowworm swarm optimization algorithm based on pattern search operator)[J].小型微型计算机系统(Journal of Chinese Computer Systems)，2011，10(21)：2130-2133.

[17] Chandrasekaran K, Simon S P, Padhy N P. Binary real coded firefly algorithm for solving unit commitment problem[J]. Information Sciences,2013, 249:67-84.

[18] 亢少将(Kang Shaojiang).萤火虫优化算法的研究与改进(Research and improvement of glowworm swarm optimization)[D].广州：广东工业大学(Guangzhou: Guangdong University of Technology)，2013.

[19] Bao Y, Hu Z, Xiong T. A PSO and pattern search based memetic algorithm for SVMs parameters optimization[J]. Neurocomputing, 2013, 117:98-106.