含气率对缓冲液囊轴向刚度特性影响的研究
2018-03-05姜荣敏
姜荣敏,张 明,蒋 锐
(南京航空航天大学 航空宇航学院,江苏 南京 210016)
1 引言
液体有效体积弹性模量是影响液压系统性能的一个重要物理参数,它对液压系统的位置精度、功率水平、响应时间和稳定性的影响显著[1]。体积弹性模量是一个软参量,是液体重要的性质参数,根据系统含气量、工作压力等参数的变化而变化[2-3]。任何弹性模量都是根据应力和应变比来进行定义的,体积弹性模量相应的应力是施加的压力,对应的应变是由此引起的体积改变量[4]。从经济性和系统工作质量的角度来看,液体中的气泡对系统的危害较大,主要体现在导致系统工作不良、加速密封件的老化、导致气蚀的发生以及引起系统振动和噪声的增加等方面[5-6]。随着工业领域的需求不断增长,国内外关于缓冲器的研究与应用也越来越成熟。一种通过小位移、小变形的新型防护装置—缓冲液囊被设计出来实现冲击保护[7]。缓冲液囊是一种在柔性密闭容器中充入液体,利用液体的近似不可压缩性来工作的一种非金属缓冲器。在液压系统动态分析、建模与仿真中,合理准确地选取液体的体积模量值是非常重要的[8]。在目前的缓冲液囊装置设计和研究中,液体的体积模量简单地取为一个常数,与系统状态无关,而这种简化使得缓冲液囊的仿真分析结果与实际情况的有一定差距[9]。因此有必要针对液体的含气率对缓冲液囊的轴向刚度特性影响进行研究。针对一种液囊缓冲装置进行研究,在分析了不同液囊含气率对液体体积模量影响的基础上,结合纯液体体积模量对缓冲液囊刚度特性的影响,进一步研究了不同液囊含气率对其轴向刚度特性的影响。
2 液囊分析模型
2.1 液囊以及机构的介绍
缓冲液囊是一种利用液体的近似不可压缩性实现冲击保护作用的一种非金属弹簧。它结构简单,制作及使用的成本相对较低;通过与内外壳的大面积接触,它能在很大程度上将内壳上的载荷传递到外壳上,从而实现冲击保护;同时,接触面积能随着外载荷的变化而变化,从而避免了接触时产生应力集中现象。经过几何简化的缓冲液囊模型,如图1所示。

图1 液囊模型示意图Fig.1 The Diagram of Fluid Bag Model
建立了一种用于单独分析液囊力学特性的缓冲液囊装置,将液囊夹持于内外壳之间,然后固定住外壳,在轴向将内壳调整到一定位置固定住,然后给液囊充压,当液囊达到预定压力时,停止充压,然后去掉内壳的约束,同时开始正式加载,记录不同载荷下所对应的液囊压力及内壳上端点轴向位移,以此获得液囊轴向刚度特性曲线及液囊压力与载荷曲线。缓冲液囊机构的整体几何模型,如图2所示。
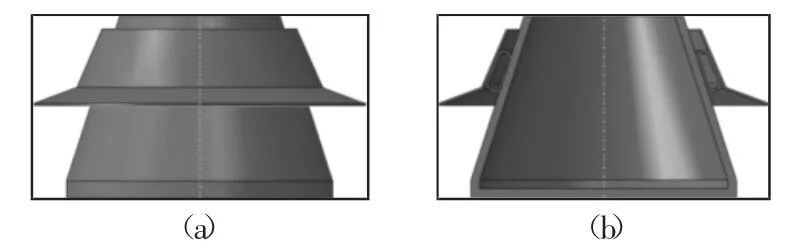
图2 机构整体模型示意图Fig.2 The Diagram of Mechanism Model
2.2 缓冲液囊机构有限元分析模型
缓冲液囊机构的仿真分析是在商用软件ABAQUS中进行的。为了模拟液囊与液体之间的相互作用,采用液囊单元与液体单元共节点的方式模拟液囊与液体之间的耦合关系。建立液囊力学特性分析有限元模型,对内外壳及液囊采用一阶壳单元S4R进行模拟,对与液囊单元耦合的液体单元则采用F3D4流体单元来进行模拟。缓冲液囊机构有限元分析模型,如图3所示。

图3 机构有限元分析模型示意图Fig.3 The Finite Element Model of Mechanism
液囊在受到挤压时,除了会与液体相互作用外,也会与内外壳相互作用,这便涉及到了液囊与内外壳之间的接触关系。由于在加载的过程中,液囊是处于不断变形中的,因此,接触状态也会不断改变,且这种状态的改变规律是未知的。所以必须建立真实的接触对来模拟液囊与内外壳之间的接触关系。建立了两个接触对:以内壳外面为主面,液囊内径面为从面建立接触对一,主从面示意图,如图4所示。以外壳内面为主面,液囊外径面为从面建立接触对二,主从面示意图,如图5所示。同时,为了使计算机能更容易收敛,分别给两个接触对设置0.1mm的容差。

图4 接触对一的主从面Fig.4 The Master Surface and Slave Surface for First Contact Pair

图5 接触对二的主从面Fig.5 The Master Surface and Slave Surface for Second Contact Pair
由于外壳是固定的,将外壳下部的表面自由度全部约束。为了方便加载集中载荷,在内壳下面单元与一个轴线上的参考点建立分布耦合关系,使得加载于坐标原点的集中载荷能均匀分布到内壳下面,边界条件及载荷耦合关系,如图6所示。内外壳所用材料为高强度钢,液囊所用材料为橡胶纤维布,缓冲液囊内部充水,假设水的温度为20℃,材料对应的材料属性,如表1所示。

图6 边界条件及载荷耦合示意图Fig.6 The Diagram of Boundary Conditions and Load Distributing Coupling

表1 模型的材料属性Tab.1 The Material Properties of Model
3 含气率对液体体积模量的影响
文献[7]所用到的液体体积模量均为理论上纯液体的体积模量。实际上,在有关液体体积模量的研究或计算中,所测到的通常并非是纯液体的体积模量,而是在含有少量气体等条件下所表现出来的弹性模量,这又被称为液体的有效体积模量。总的来说,影响液体体积模量的主要因素有液体含气率、温度、压力及液体种类等,且液体的有效体积模量随着含气率的增大而减小,随着液体温度的升高而减小,随着液体压力的增大而增大[10]。
液体所含气体主要分为两部分,一种对液体的体积模量无影响,主要以溶解状态存在;另一种则是以气泡的形式游离于液体中的空气,对其体积模量有很大的影响。不同种类液体的空气溶解率是不同的,如石油基液压油是(5~7)%,磷酸酯是5%,水和乙二醇混合液是(1~2)%[5]。
由亨利定律可知,气体在液体中的溶解量与绝对压力呈正比例关系,纯液体的体积模量随着压力的增大而增大。同时,在密闭的容器内,压力增大,空气的溶解量也增大,导致以气泡等游离状态的空气含量减少,从而使液体的体积模量增大。因此,当含气液体的压力变化时,会以这两种方式影响液体的体积模量[4]。
在体积为V0的含气液体中,若混入的气体体积为Vg,则纯液体的体积可表示为:Vl=V0-Vg(1)
当压力增加ΔP时,含气液体的体积减少量ΔV,即为纯液体体积减少量ΔVl和气体体积减少量ΔVg之和,则:

由体积模量的关系式可知,含气液体的有效体积模量可表示为:
气体的体积模量可表示为:Kg=-VgΔP/ΔVg(4)
纯液体的体积模量可表示为:Kl=-VlΔP/ΔVl(5)
结合式(2)~式(5),可得含气液体的有效体积模量K的表达式为:
对于缓冲液囊而言,当充压结束时,液囊内的液体可能还会混有少量空气,这会影响液体的有效体积模量。根据定义,体积模量分为正切体积模量和正割体积模量两种。当液囊被压缩时,空气在液囊内被溶解和压缩的瞬时变化过程是复杂的,而正割体积模量则表示了液囊内液体在一定压力范围内的平均体积模量,因此选用正割体积模量来定义液体和空气。根据式(3)可知,有:

式中:Ke—含气液体的有效体积模量;V1—液囊压力p1为时液体和气体的总体积;p0—标准大气压;p1—液囊的工作压力。
当液囊被压缩时,空气在液囊内的状态比较复杂。因此,假定空气在液囊内的变化情况为先溶解再压缩。溶解过程遵循亨利定律,压缩过程遵循气体状态方程[4]。
由于液囊的加载过程是短暂的,因此,可以将缓冲液囊受压这一瞬间视为绝热过程。当液囊充压时,液体中混杂的空气的状态方程为:
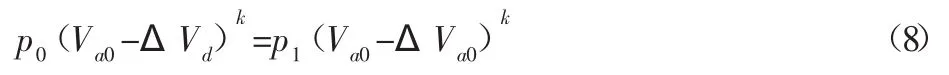
式中:Va0—液囊内所含空气体积;ΔVd—液囊压力由p0变为p1时多溶解的气体体积;ΔVa0—空气因溶解和压缩减小的体积;κ—绝热指数,取 κ=1.39。
解方程(8),得到:
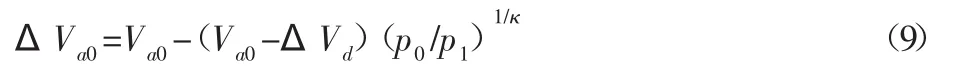
由文献[2]可知,若在大气压下空气在液体中的溶解度为δ0,当空气的绝对压力为p1,其溶解度为δ=10δ0Δp,其中Δp=p1-p0。因此,有:

式中:α—大气压下液囊的含气率,α=Va0/V0。
对式(6)进行变换,可得:

式中:Vl—纯液体体积;Kl—纯液体的体积模量;Vg—大气压下液囊内的空气体积;Kg—空气的体积模量。
联解式(7)、式(9)~式(11),可得:

液囊内所充液体为水,水的体积模量Kl=2200MPa。由于液囊内含有的空气是少量的,因此假设含气率分别为0.01%、0.02%、0.04%、0.06%、0.08%、0.10%、0.20%、0.40%、0.60%、0.80%、1.00%、2.00%,则由式(12)推导得到的不同含气率下液体有效体积模量随压力变化曲线,如图7所示。

图7 液体有效体积模量随压力变化曲线图Fig.7 The Diagram of Effective Bulk Modulus and Bag Pressure
由图7可知,在(0~10)MPa范围内,随着液囊压力的不断增大,液体有效体积模量也不断增大;当含气率<0.10%时,含气率越高,相同压力下的有效体积模量越小;当液囊压力增大到一定值之后,有效体积模量逐渐趋于一个稳定值;且含气率越高,有效体积模量达到稳定值所需的压力越大;当含气率>0.10%时,含气率越高,有效体积模量随压力变化曲线的线性特性越明显;在相同液囊压力的情况下,含气率越高,有效体积模量越小。
4 含气率对液囊轴向刚度特性的影响
用以下方法来研究不同含气率下液囊的轴向刚度特性:首先,计算出特定含气率的液体压力为P1时对应的有效体积模量K1,然后计算出液囊在充入体积模量为K1的纯液体、压力达到P1时对应的内壳轴向载荷F1与位移U1;改变含气液体的压力为P2,得到此时的有效体积模量K2,然后计算液囊充入体积模量为K2的纯液体、压力达到P2时对应的内壳轴向载荷F2与位移U2;通过不断改变含气液体的压力,最终得到不同液体体积模量及压力下的内壳轴向载荷与位移,从而得到一系列孤立的数据点,最后用这些孤立的点拟合出相应的曲线,从而得到液囊的轴向刚度及压力变化曲线。计算出液囊初始含气率分别为0.04%、0.06%、0.08%、0.10%、0.40%、0.60%、0.80%、1.00%时液囊的轴向刚度特性,并与纯液体下的液囊刚度特性进行比较,计算结果,如图8、图9所示。

图8 内壳轴向位移与载荷曲线图Fig.8 The Diagram of Axial Displacement of Inner Shell and Axial Load

图9 液囊压力与载荷曲线图Fig.9 The Diagram of Bag Pressure and Axial Load
由图8可知,随着载荷的不断增大,不同含气率下的液囊轴向刚度不断增大,直至轴向刚度最后保持不变。初始含气率的不同也影响着液囊的轴向刚度特性:含气率越高,液囊轴向刚度特性的非线性越明显,且非线性阶段均在一定载荷范围内(约为250kN);然而,当含气率<0.1%(包括纯液体)时,不同含气率下的液囊轴向刚度差异较小,当含气率>0.1%时,不同含气率下的液囊轴向刚度差异较明显。经分析,当含气率<0.1%时,由于此时液囊含气量相对较少,气体对液体体积模量的影响也相对较小,液体的初始有效体积模量较大,增大的空间较小,随着液囊的不断压缩,液体的有效体积模量能迅速趋于一个稳定值,因而液囊的轴向刚度特性也能迅速趋于线性;当含气率>0.1%时,由于此时液囊含气量相对较多,因此,气体对液体体积模量的影响相对较大,随着液囊的不断压缩,液体的有效体积模量增大的空间较大,增大到稳定值所需的时间相对较长,因此液囊的轴向刚度特性在载荷<250kN范围内非线性较明显,在载荷>250kN时趋于线性。
由图9可知,不同含气率下的液囊压力与载荷曲线呈现出了良好的线性特性。当含气率<0.1%时,不同含气率下(包括纯液体)的液囊压力与载荷曲线基本重合,当含气率>0.1%时,随着含气率的增大,液囊压力与载荷曲线的曲率逐渐减小,不同曲线间的曲率差值总体较小。由图8与图9可知,当载荷约为125kN时,不同含气率下(包括纯液体)的内壳轴向位移均约为-0.35mm,液囊压力均约为2.5MPa,满足液囊初始充压的载荷。这说明,在液囊不同含气率条件下,125kN也为该液囊的“临界载荷”。
5 结论
(1)讨论了含气率对液体体积模量的影响。在液囊压力不是太高的情况下(<10MPa),随着液囊压力的不断增大,液体有效体积模量也在不断增大;当含气率<0.10%时,含气率越高,相同压力下的有效体积模量越小;当液囊压力增大到一定值之后,有效体积模量逐渐趋于一个稳定值;且含气率越高,有效体积模量达到稳定值所需的压力越大;当含气率>0.10%时,含气率越高,有效体积模量随压力变化曲线的线性特性越明显;在相同液囊压力的情况下,含气率越高,有效体积模量越小。(2)研究了含气率对缓冲液囊轴向刚度及压力变化特性的影响。随着载荷的不断增大,不同含气率下的液囊轴向刚度不断增大,最后趋于一个稳定值;含气率越大,轴向刚度趋于稳定值所需载荷越大,且刚度曲线的非线性越明显。液囊压力与载荷曲线呈现出了良好的线性特性;当含气率<0.10%时,不同含气率下(包括纯液体)的液囊压力与载荷曲线基本重合,当含气率>0.10%时,随着含气率的增大,液囊压力与载荷曲线的曲率逐渐减小;不同曲线间的曲率差值总体较小。当液囊初始充压为2.5MPa、内壳轴向位移为-0.35mm时,对应的外载荷约为125kN,这也是该液囊的“临界载荷”,且这一数值不受液体体积模量及液囊含气率的影响。(3)在分析液囊含气率对其轴向刚度及压力变化特性的影响规律时,采用了一种近似算法,为了更真实地分析液囊含气率对液囊轴向刚度及压力变化特性的影响规律,下一个研究方向是采用流固耦合的方法,建立真实的气液固三相耦合的分析模型进行求解。
[1]George H.F.,Barber A.What is bulk modulus and when is it important[J].Hydraulic and Pneumatics,2007(7):34-39.
[2]冯斌,龚国芳,杨华勇.液压油弹性模量提高方法与试验[J].农业机械学报,2010,41(3):219-222.(Feng Bing,Gong Guo-fang,Yang Hua-yong.Method and experiment for increasing effective fluid bulk modulus in hydraulic systems[J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(3):219-222.)
[3]孙海平,邓景流.工作介质弹性模量对液压系统压力瞬变的分析[J].华南理工大学学报:自然科学版,1997,25(7):112-116.(Sun Hai-ping,Deng Jing-liu.Analyses of influence of bulk modulus of actuating medium on pressure transients in hydraulically driving system[J].Journal of South China University of Technology:Natural Science,1997,25(7):112-116.)
[4]陈超.液压油体积弹性模量在线检测装置设计及研究[D].杭州:浙江大学,2008.(Chen Chao.Design and study of the online measuring device for hydraulic oil bulk modulus[D].Hangzhou:Zhejiang Universiy,2008.)
[5]祁冠方,虞万海,胡文续.气泡对液压系统的危害及其对策[J].机床与液压,1999(5):50-51.(Qi Guan-fang,Yu Wang-hai,Hu Wen-xu.The harm of bubbles to the hydraulic system and the strategies[J].Hydromechatronics Engineering,1999(5):50-51.)
[6]胡天鹤,阿达依·谢尔亚孜旦.电化学光整加工过程产生的气泡行为研究[J].机械设计与制造,2014(8):95-97.(Hu Tian-he,A dayi.Xie er ya zi dan.Study on the behavior of bubbles produced in electrochemical finishing maching[J].Machinery Design&Manufacture,2014(8):95-97.)
[7]Zhang Ming,Jiang Rui,Nie Hong.Analysis of stiffness characteristics of a new fluid bag for axial shock protection[J].Journal of Vibroengineering,2015,17(2):587-601.
[8]Yu Jing-hong,Chen Zhao-neng,Lu Yuan-zhang.The variation of oil effective bulk modulus with pressure in hydraulic systems[J].Journal of Dynamic Systems Measurement and Control,1994,116(1):146-150.
[9]Ali Volkan Akkaya.Effect of bulk modulus on performance of a hydrostatic transmission control system[J].Sadhana,2006,31(5):543-556.
[10]王静,龚国芳,杨华勇.油液体积模量的研究与在线测试[J].机械工程学报,2009,45(7):120-125.(Wang Jing,Gong Guo-fang,Yang Hua-yong.Research and online measurement of bulk modulus of hydraulic oil[J].Journal of Mechanical Engineering,2009,45(7):120-125.)
