周向整体式MEFP战斗部结构设计研究
2018-03-05郑灿杰陈智刚付建平张孝中王维占兰宇鹏
郑灿杰,陈智刚,付建平,张孝中,王维占,兰宇鹏
(1.中北大学地下目标毁伤技术国防重点学科实验室,山西 太原 030051)(2.山东特种工业集团,山东 淄博 255200)
MEFP[1](多爆炸成型弹丸)技术的产生实现了战斗部一次作用产生多个弹丸的功能,提高了弹丸命中目标的概率,大大提升了战斗部的作战效能,基于其相比于单个EFP(爆炸成型弹丸)战斗部更易命中且易摧毁目标的优势,现已在国内外展开了广泛研究[2-5],MEFP战斗部的技术也越来越成熟。目前,MEFP的常见模式[6]有组合式、变形罩式、切割式、整体多罩式。
本文设计了一种周向整体式MEFP战斗部,即在战斗部外壳面沿圆周方向分层均匀布置药型罩,在爆炸载荷作用下药型罩翻转形成多束EFP,对周围空间目标进行毁伤。为了保证在空间形成均匀的杀伤场,周向整体式MEFP战斗部在壳体结构上可做一定改进。本文采用上一层药型罩与下一层药型罩位置互相交错、每一层药型罩数量相等的方案,可提高多束EFP在空间分布上的均匀性。采用这种MEFP战斗部,可以增大弹药有效杀伤半径,在较大范围内重点打击威胁目标,提高战斗部毁伤效能。实践证明,这种战斗部对付舰船和空中目标等轻型装甲是非常有效的[7]。
1 仿真计算模型
1.1 初步方案设计
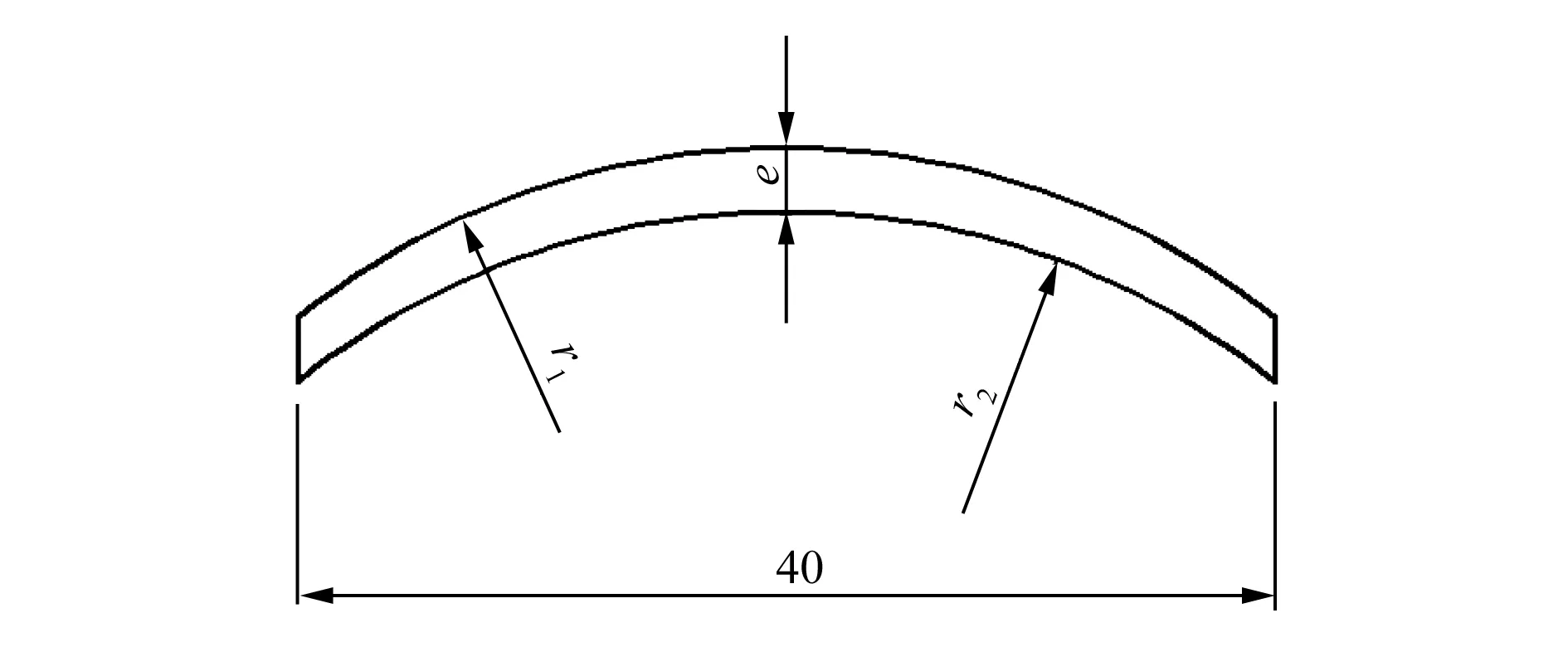
图1 药型罩结构示意图
1.2 有限元模型与算法
本文利用TrueGrid软件构建有限元模型,通过其与LS-DYNA软件的接口,将TrueGrid软件生成的模型文件导入LS-DYNA软件中进行计算。由于结构的几何形状关于XOZ平面和YOZ平面对称,所以在施加对称约束的情况下可利用TrueGrid软件建立战斗部的1/4有限元模型,如图2所示。
在数值模拟计算中,材料参数的选取直接影响到计算结果的精确性,不同材料模型对材料的描述是不同的,这些区别都会影响仿真计算的结果。因此,选择合理的本构模型及材料参数是保证计算结果准确的必要前提。本文所讨论的MEFP战斗部主要包括炸药和药型罩,爆炸作用介质为空气。

图2 战斗部1/4有限元模型
1)炸药。
主装药采用8701炸药,其密度为1.717g/cm3,爆速为8 425m/s,采用* Mat_High_Explosive_Burn模型和JWL(Jones-Wilkins-Lee)状态方程进行数值模拟计算。8701炸药的JWL状态方程各项参数[8]见表1。

表1 8701炸药JWL状态方程参数
其中A,B,R1,R2为输入参数;E0为单位体积爆轰产物的内能。
2)药型罩。
药型罩对成型聚能侵彻体的质量好坏起决定作用,直接决定了其毁伤性能的优劣。目前采用最多的药型罩材料是紫铜,其密度高,塑性优良,形成的侵彻体破甲效果优异。因此,本文药型罩材料选取紫铜,材料模型为MAT_JOHNSON_COOK,它在考虑了金属材料承受大应力、高应变率以及高温的情况下,用来描述动态响应过程和材料变形问题。紫铜的模型参数见表2。
从正常发酵大头菜酱液(标号为N)中和长膜大头菜酱液(标号为M)中共20株酵母菌株培养于YPD液体培养基,在28 ℃培养1天,肉眼观察菌落形态为:部分试管内溶液澄清,表面无膜生成,底部没有沉淀;部分试管液体表面有膜形成,底部有沉淀存在,溶液有一定程度的浑浊。将20株酵母菌划线在PDA琼脂培养基上,28 ℃培养1天,菌落形态为:菌落颜色呈乳白色;菌落从侧面观察有凸起也有扁平,表面粗糙有褶皱,也有表面光滑;菌落边缘有长出毛边,也有呈现锯齿状,或者整齐无边。分离菌株菌落形态观察结果汇总入表2,菌落形态见图1。

表2 药型罩紫铜状态方程参数
其中:ρ为材料密度;G为材料剪切模量;c为冲击波速度;S1,S2,S3为曲线斜率系数;γ0为Gruneisen系数;α是γ0的一阶体积修正系数。
3)空气。
对于Euler算法和多物质ALE流固耦合算法[9]来说,建模还需要在侵彻体飞行的整个区域范围内添加空气域,并在边界点上施加压力流出的边界条件,避免边界效应对计算精度的影响。空气域所用的材料模型为MAT_NULL,采用的线性多项式状态方程为EOS_LINEAR_POLYNOMIAL。表3是进行数值计算时空气所用的材料参数。

表3 空气的材料参数
其中RO为质量密度;PC为压力切断系数;MU为动态粘度系数;TEROD和TEROD为张力侵蚀和压缩侵蚀的相对量,为0时不起作用;YM为杨氏模量;PR为泊松比。
本文采用多物质耦合ALE算法[9]来模拟聚能装药作用的药型罩成型过程,并建立足以覆盖整个射流范围的空气域。为避免压力在边界上的反射,在模型的边界节点上施加压力透射边界条件。
为节约计算时间,根据对称性可取战斗部模型的1/4结构来建立三维模型进行运算,并在模型的对称面上施加对称约束条件。计算网格[10]均采用六面体实体单元,炸药、药型罩、空气采用ALE算法,战斗部壳体、靶板采用Lagrange算法,它们之间的相互作用采用流固耦合算法。计算模型几何参数如下:装药口径为55.0mm,装药高度为51.6mm,药型罩口径为51.6mm,药型罩高度为17.2mm。
2 数值模拟与结果分析
2.1 排列方式对成型过程的影响
在研究药型罩的排列方式对周向MEFP成型影响时,本文设计了两种排列方案。方案1是药型罩每层平行排列在战斗部装药结构上;方案2是药型罩每层交错排列在战斗部装药结构上,计算模型如图3所示,在装药结构与药型罩参数不变的情况下,只改变药型罩分布方式。设计的仿真方案数据如下:装药外接圆柱直径130mm,药型罩轴向间距10mm,药型罩分为3层,每层分布8个罩,药型罩口径40mm,药型罩外曲率半径30mm,药型罩厚度3mm,无战斗部壳体,采用中心轴三点起爆方式。2种方案的子EFP成型对比见表4。

图3 计算模型
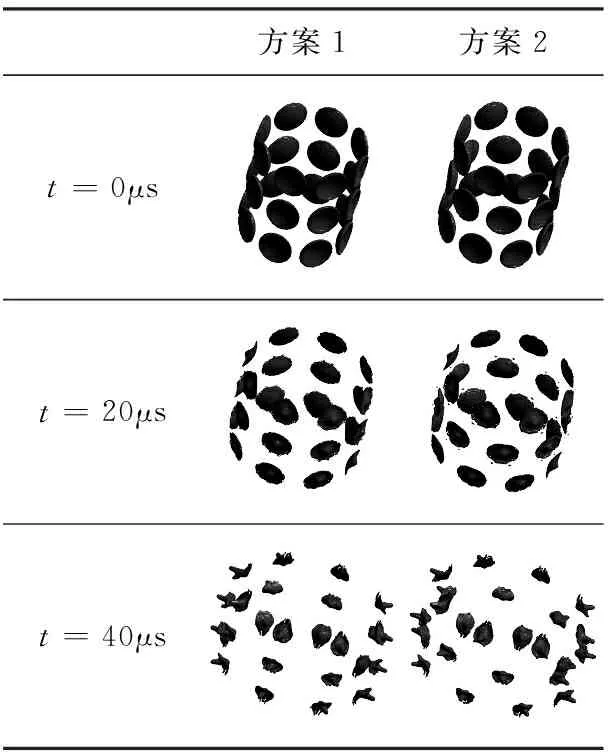
表4 2种方案成型过程
从表4可以看出,在炸药起爆后0μs时刻为初始状态,药型罩在0~20μs之间受炸药爆炸产生的爆轰波冲击作用,压垮变形,向前高速运动;在20μs时,药型罩开始翻转,中间形成凸起;在40μs时,形成了24个成型完整的、具有一定发散角的子EFP。对比可知,方案2比方案1所形成的子EFP散布更密集,可提高命中率。此外,二者所形成的上下层子EFP都发生偏转,中间层未偏转。
方案1与方案2所形成的中间层子EFP轴向速度对比曲线如图4所示,上下层子EFP的速度对比曲线如图5所示。
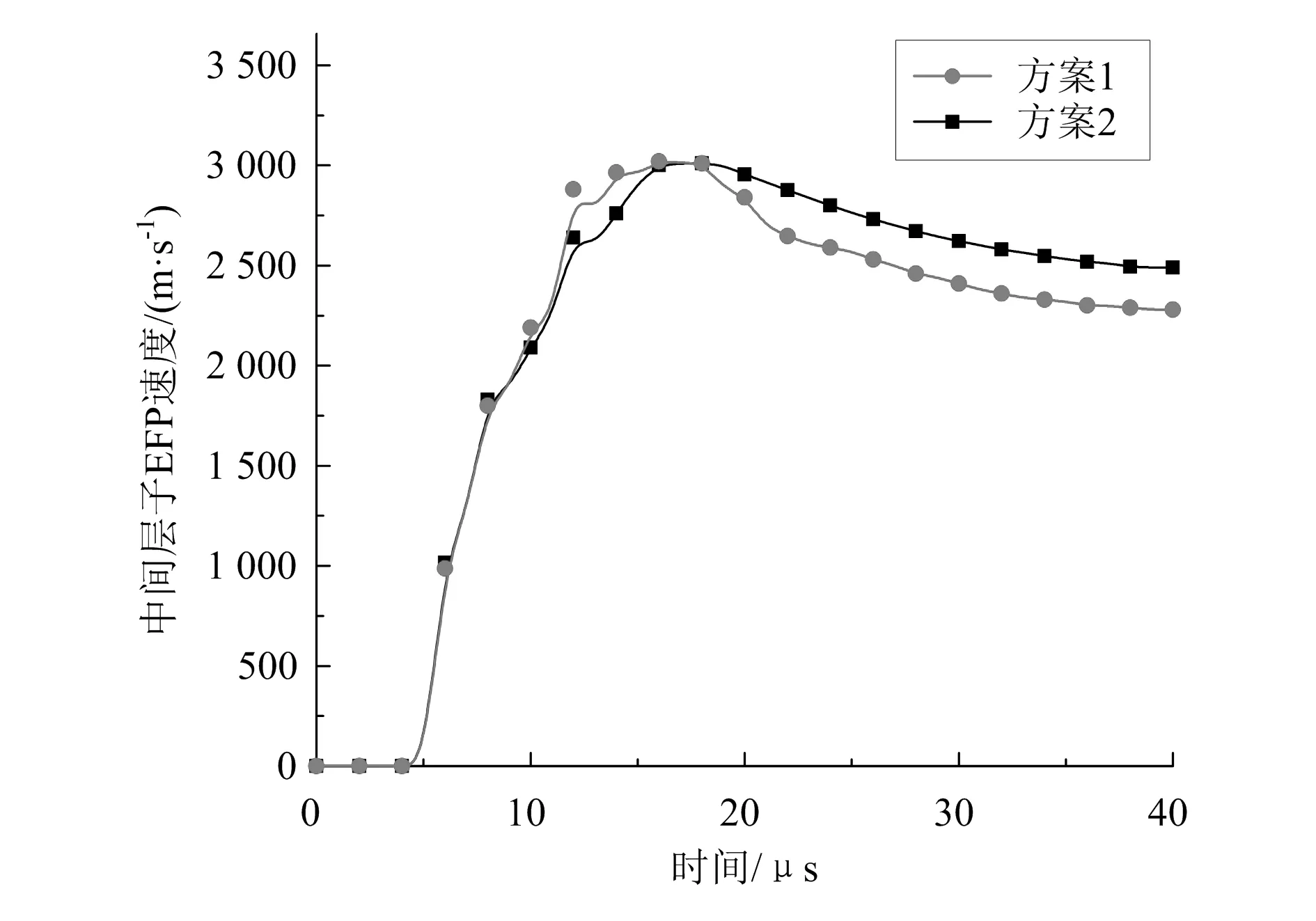
图4 中间层子EFP轴向速度对比曲线
从图4可以看出,时间从0μs增加到30μs,方案1与方案2的中间层子EFP速度都呈先增大后减小的趋势,最后趋于稳定。在40μs时,方案1的子EFP速度为2 260m/s,方案2的子EFP速度为2 490m/s。
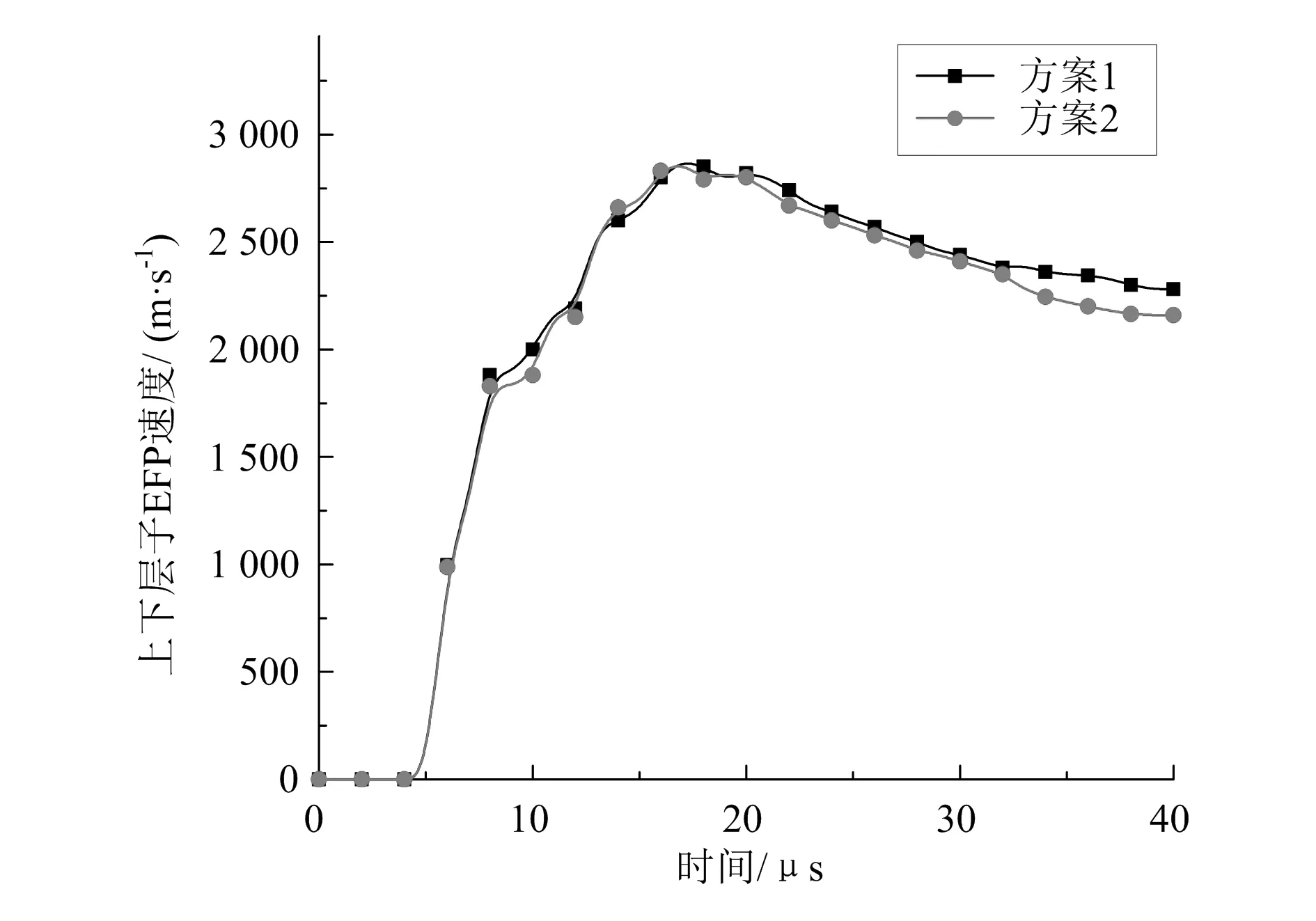
图5 上下层子EFP轴向速度对比曲线
从图5可以看出,时间从0μs增加到30μs,方案1与方案2所形成的上下层子EFP速度都呈先增大后减小的趋势,最后趋于稳定。在40μs时,方案1的子EFP速度为2 160m/s ,方案2的子EFP速度为2 280m/s。
综上所述,方案2比方案1所形成的子EFP散布密集更好,在弹目交汇时,更易击中目标。无论是中间层还是上下层所形成的子EFP的速度,方案2都优于方案1。因此,交错式周向结构所形成子EFP的综合性能更好。
2.2 层数对成型过程的影响
在研究药型罩的分布层数对周向MEFP成型影响时,本文设计了3种结构进行比较。单层结构是在装药结构上周向分布一层药型罩;双层结构是在装药结构上周向交错式分布两层药型罩;三层结构是在装药结构上周向交错式分布三层药型罩。单层结构采用中心轴点起爆,双层结构采用中心轴两点起爆,三层结构采用中心轴三点起爆。3种结构所形成的子EFP形态对比见表5,所形成的子EFP轴向速度曲线对比如图6所示。
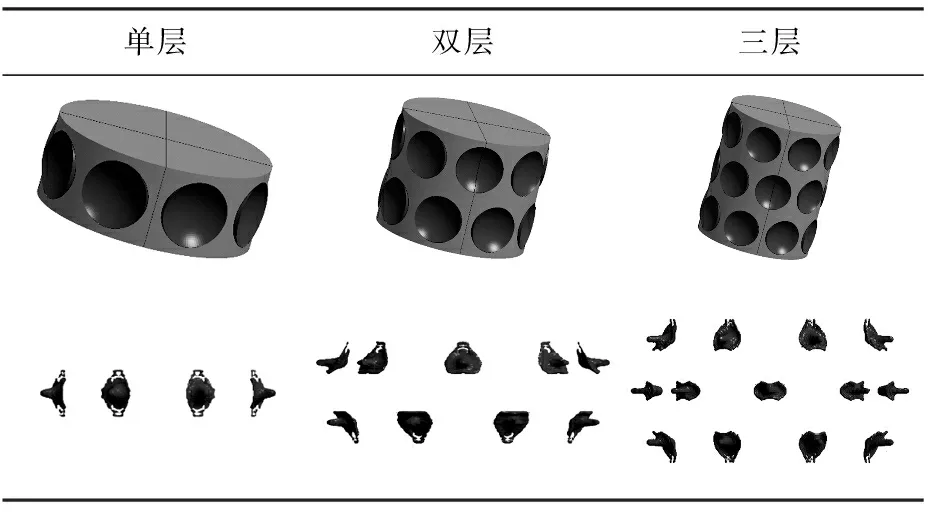
表5 3种结构子EFP形态图
从表5可以看出,单层结构形成的子EFP形态最佳;双层结构在爆轰波的叠加作用下,所形成的两层子EFP都发生偏转;而三层结构在爆轰波的叠加作用下,所形成的上下层子EFP都发生偏转,中间层子EFP未偏转。
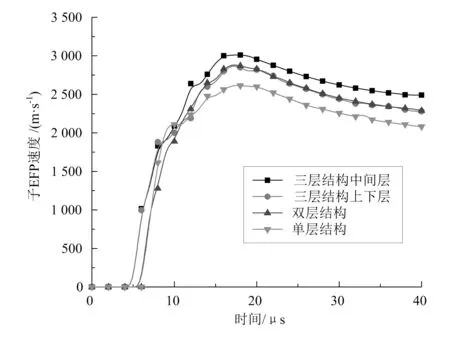
图6 3种结构子EFP轴向速度曲线对比图
从图6可知,在接近20μs时,3种结构所形成的子EFP速度都增大至最大值,随后开始逐渐减小,最后趋于稳定。但单层结构在40μs时所形成的子EFP速度最小。总之,随着层数的增加,所形成的子EFP速度就越大。
2.3 起爆方式对成型过程的影响
在研究起爆方式对周向MEFP成型影响时,本文采用了两种起爆方式,分别为装药中心轴线起爆和中心轴三点起爆。采用这两种起爆方式对三层周向交错式MEFP进行数值模拟,其模拟结果对比如图7所示,子EFP轴向速度对比曲线如图8所示。

图7 子EFP形态对比图
从图7可以看出,线起爆所形成的子EFP的长径比更大。由图8可知,无论是中间层还是上下层,形成的子EFP轴向速度都随时间的增加先增大后减小,最后趋于稳定,而线起爆方式形成的各层子EFP轴向速度比三点起爆方式所形成的子EFP轴向速度都大。
3 结论
本文通过建立MEFP战斗部数值模型,分析了药型罩排布方式、排列层数、起爆方式对侵彻体成型的影响,主要得到以下结论:
1)药型罩交错式排列比平行式排列所形成的子EFP散布密集更好,在弹目交汇时,更易击中目标。无论是中间层还是上下层所形成的子EFP的速度,交错式都优于平行式。
2)从MEFP排列层数看,在接近20μs时,3种排列层数战斗部所形成的子EFP速度都增大至最大值,随后开始逐渐减小,最后趋于稳定。随着层数的增加,所形成的子EFP速度也越大。
3)从起爆方式来看,线起爆方式比三点起爆方式所形成的子EFP的长径比大且轴向速度也高。
[1] 邢栋.MEFP成型影响因素分析与研究[D].沈阳:沈阳理工大学,2013.
[2] 付璐,尹建平,王志军,等.MEFP 战斗部结构的正交优化设计[J].火力与指挥控制,2012,37(3):28-30.
[3] 袁建飞,苏健军,王辉,等.复合药型罩EFP的形成及数值模拟[J].火炸药学报,2010,33(1):83-88.
[4] 赵长啸,龙泉,隋元松.起爆方式对整体式MEFP 战斗部参数的影响[J].解放军理工大学学报(自然科学版),2012,13(5):10-13.
[5] 黄正祥.聚能装药理论与实践[M].北京:北京理工大学出版社,2014.
[6] 张先锋,陈惠武,赵有守.EFP冲击引爆带壳炸药数值模拟研究[J].弹道学报,2006,18(1):90-92.
[7] 彭飞,余道强,阳世清,等.含能破片战斗部毁伤效应研究[J].含能材料,2011,4(19):450-453.
[8] 石少卿. ANSYS/LS-DYNA在爆炸与冲击领域内的工程应用[M].北京:中国建筑工业出版社,2011.
[9] 李裕春.ANSYS/LS-DYNA10.0基础理论与工程实践[M].北京:中国水利水电出版社,2006.
[10] 时党勇,李裕春,张胜民.基于ANSYS/LS-DYNA8.1进行显式动力分析[M].北京:清华大学出版社,2005.
