基于改进leader-follower策略的AGV多驱动单元协同控制

武 星，赵 龙，武靖洋，陈 华，楼佩煌

(1.南京航空航天大学机电学院，江苏 南京 210016)(2.河海大学机电工程学院，江苏 常州 213022)

与单个机器人相比，多机器人系统具有很多优势[1-2]，如可用更少的时间和以更高的质量完成预定作业，可完成超出单个机器人感知范围或负载能力的任务，可降低机器人个体的结构复杂度和研制成本，并可为复杂任务提供柔性的解决方案。

随着重型机械、港口物流等行业希望采用自动导引车(AGV)搬运超大超重的物体，研制多轮驱动的重载AGV逐渐引起国内外学者的研究兴趣[3-5]。采用多个驱动单元合作搬运超大超重的物体，可借鉴多机器人队形控制方法[6-9]。leader-follower策略[6-8]将移动机器人分为leader和follower，leader有能力感知环境，规划导引路径和运动轨迹，从而将队形控制问题转化为followers跟踪leader的位置和方向的问题。而虚拟结构法[9]将整个队形视为一个刚体，再将虚拟结构的整体运动转化为每个机器人的期望运动。

笔者对在融合短视距传感器、小功率电机和轻量化底盘的基础上设计拉动重载AGV的差速驱动单元进行了研究[5]。在此基础上，本文针对多个差速驱动单元组成的AGV，将其每个驱动单元都视为一个机器人，则该AGV就是由多个驱动单元组成的多机器人系统。借鉴多机器人队形控制方法，提出一种基于虚拟结构法和leader-follower策略的多驱动单元协同控制技术。

1 系统控制策略

对于由3个及以上的差速驱动单元构成的多驱动AGV，其路径跟踪控制方式不同于普通AGV。由于AGV车体对驱动单元的刚性约束，多驱动AGV在进行自动导引时，难以同时实现所有驱动单元对导引路径的跟踪控制。为了消解多个驱动单元之间的运动冲突，部分驱动单元(随动驱动单元)将不再进行路径跟踪，而是跟随导引驱动单元进行协调运动，避免AGV车体刚性约束下驱动轮打滑甚至卡死。可见，导引驱动单元与随动驱动单元之间的运动关系，非常类似于多机器人队形控制中的leader-follower策略。

针对图1所示的多驱动AGV，采用一种改进的leader-follower队形控制策略，选择前面第一个驱动单元为主leader单元，后面第三个驱动单元为次leader单元，中间第二个驱动单元为follower单元。将不同驱动单元中心点之间的距离l12,l23,l13作为leader-follower模型中的距离参数；将各个驱动单元与车体运行方向的夹角α1,α2,α3作为leader-follower模型中的姿态角参数。利用虚拟结构法描述AGV车体对驱动单元的刚性约束，各驱动单元所需满足的虚拟编队要求即为AGV整体在平面上做刚体运动时所需满足的几何约束。

图1 多驱动AGV的布局示意图

如图2所示，这种改进的leader-follower队形控制策略具体如下：主leader单元作为AGV整体运动的参考点，通过路径跟踪引导AGV整体按照预定路径运动。次leader单元在进行路径跟踪的同时需要维持与主leader单元之间的相对距离l12。follower单元不对导引路径进行跟踪，而是根据主leader单元、次leader单元的运动，调节自身差速控制量，以保持与主leader单元的相对距离l13、与次leader单元的相对距离l23不变，并维持满足AGV整体进行刚体平面运动所需的相对姿态角度关系。

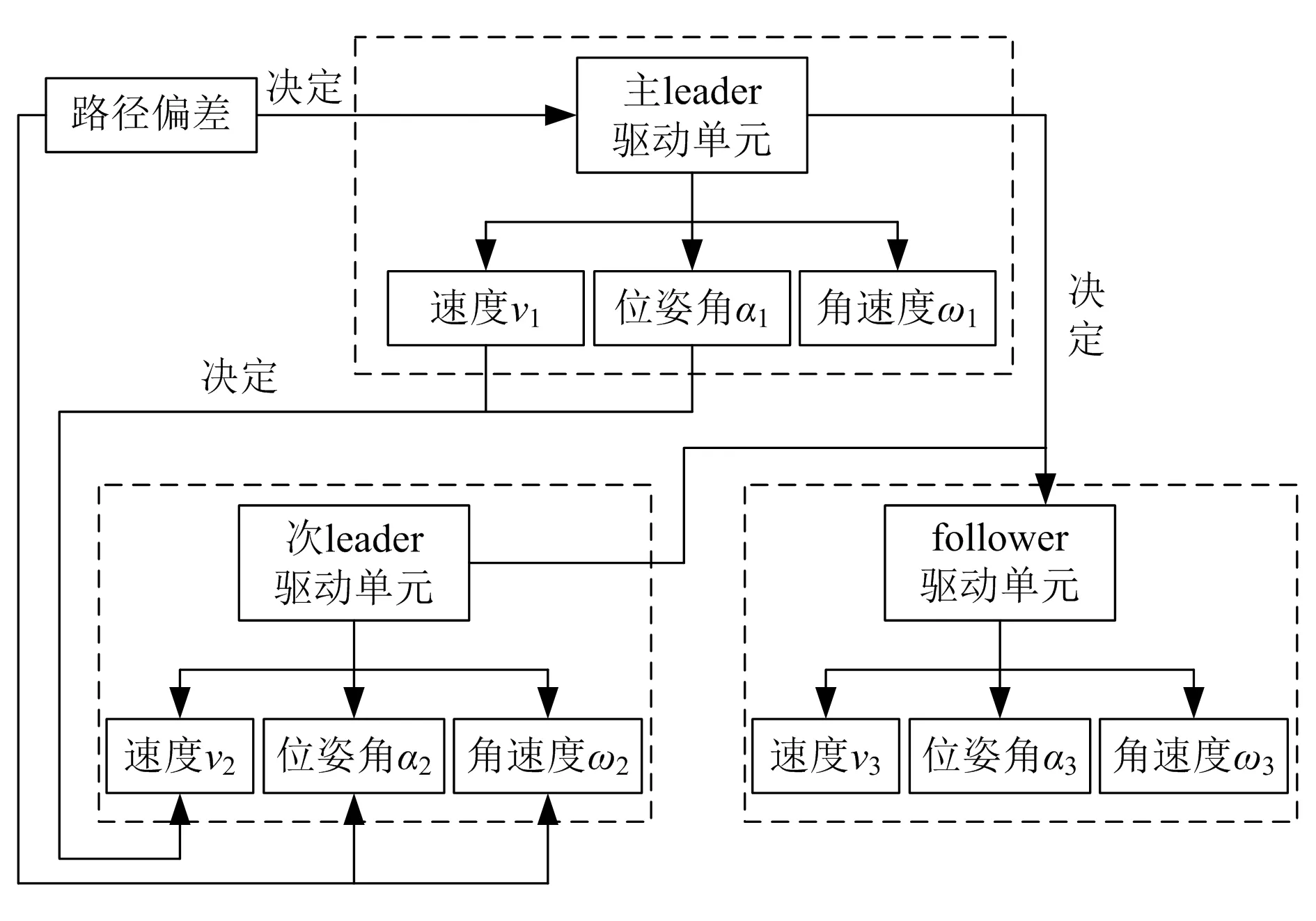
图2 改进的leader-follower策略

2 协同控制率

利用虚拟结构法描述AGV车体对驱动单元的刚性约束，将每个驱动单元简化为单个刚体，则其运动控制量表示为线速度和角速度u=[v,ω]。以第三个驱动单元中心为坐标系原点，各驱动单元中心连线为x轴，建立AGV运动控制坐标系，如图3所示。

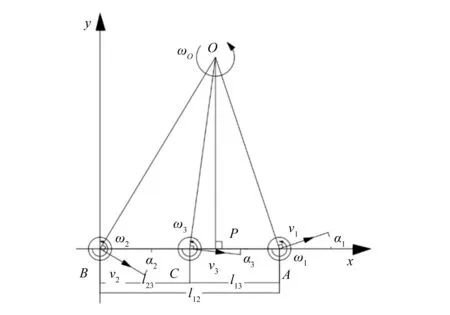
图3 多驱动AGV的运动学简图

设3个驱动单元的中心点坐标为A(x1,y1)、B(x2,y2)和C(x3,y3)。α1,α2,α3为各驱动单元的姿态角，以x轴正向到驱动单元线速度方向的顺时针方向为正。ω1,ω2,ω3分别为各驱动单元的角速度，ω0为AGV车体的角速度，顺时针为正。点O(xO,yO)为各驱动单元的速度瞬心。

多驱动AGV的运动学方程为：

(1)

式中：i=1,2,3，分别代表前面的主leader单元、后面的次leader单元、中间的follower单元。

主leader单元的路径跟踪控制只需考虑其自身的路径偏差状态，可采用单个移动机器人的路径跟踪控制方法[10]。本文主要研究次leader单元和follower单元的运动控制律。为了保证多个驱动单元运动的协调性，follower单元需要与leader单元满足刚体平面运动约束。首先是主leader单元和次leader单元之间的相对距离l12约束：

l12=x1-x2

(2)

对式(2)求导可得：

(3)

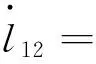
(4)

对于follower单元，它需要满足的约束有两个方面。

第一个是其与两个leader单元之间的相对距离约束：

(5)

对式(5)求导可得：

(6)

(7)

第二个是follower单元与两个leader单元之间的相对姿态角约束。针对两个leader单元的姿态角，根据刚体运动学原理，为了保持多驱动单元的队形约束，计算follower单元所需处于的理想姿态角状态。

(8)

由此可得速度瞬心O的坐标为：

(9)

式中：l12=l13+l23，为主leader单元与次leader单元中心点之间的距离。

由式(8)可得follower单元的理想姿态角为：

(10)

对式(10)求导可得：

(11)

AGV车体的角速度为：

(12)

考虑到ωO符号的正负与速度瞬心的纵坐标符号相反，并结合式(9)有:

(13)

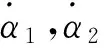
(14)

其中，

(15)

(16)

式中：Δv1,Δv2为主leader单元和次leader单元的速度差控制量，等效于角速度控制量；W为差速驱动单元两驱动轮的间距。利用式(14)可根据leader单元的速度差控制量计算follower单元的线速度、角速度控制量。

3 仿真实验

根据差速驱动单元的实际物理结构设置多驱动AGV的系统参数，具体见表1。针对多驱动AGV进行路径跟踪仿真实验，仿真实验的采样周期为0.04s。假设follower单元的运行状态不会影响leader单元，即AGV的整体运行状态仅取决于leader单元。根据该假设，由于AGV车体的刚性约束，仿真过程中follower单元在每个采样周期的路径偏差，不会跨越采样周期进行累积。

多驱动AGV的初始偏差状态为大偏差状态，主leader单元的初始偏差为：路径距离偏差ed1=30mm，路径角度偏差eθ1=15°；次leader单元的初始偏差为：路径距离偏差ed2=30mm，路径角度偏差eθ2=-5°。在路径跟踪中leader单元的路径偏差变化过程如图4所示。

图4 leader单元的路径偏差数据

参数值驱动单元间距l/mm600AGV运行速度v/(mm·s-1)800驱动轮间距W/mm300驱动轮半径R/mm62电机最大加速度amax/(r·s-2)50电机最高转速nmax/(r·min-1)3000

在此过程中，follower单元的路径偏差变化过程如图5所示。图5(a)中的虚线和实线分别表示为了满足刚体运动学原理follower单元所需的理想姿态角和实际姿态角，图5(b)中的虚线和实线分别表示follower单元所需的理想距离偏差和实际距离偏差。理想距离偏差是指根据主、从leader单元的距离偏差，由运动学约束计算follower单元相对于导引路径的理论距离偏差，其与实际距离偏差的差值定义为路径距离偏差的误差。

图5 follower单元的运动控制数据

由图可知，当主leader单元和次leader单元的路径跟踪轨迹分别在0.40s和0.64s发生较大变化时，follower单元也随之进行了运动状态的调整，并在1.00s时与leader单元同时达到稳态。在路径跟踪的暂态过程中，最大姿态角误差为0.549 4°；在路径跟踪的稳态时，姿态角误差为0.159 5°，路径距离偏差的误差为0.089 1mm。由此可见，follower单元在路径跟踪过程中具有很小的协同运动误差。

4 结束语

多机器人系统可完成单个机器人无法完成的任务，采用合作搬运方式可运输远超过单个机器人负载能力的超大超重物体，这是将多机器人系统方法应用于重载AGV的一种尝试。本文针对多个差速驱动单元组成的AGV，提出一种基于虚拟结构法和leader-follower策略的多驱动单元协同控制技术，显著减小了follower单元的协同运动误差，仿真实验结果验证了该技术的有效性。

[1] 原魁, 李园, 房立新. 多移动机器人系统研究发展近况[J].自动化学报, 2007, 33(8): 785-794.

[2] WANG Guanghua, LI Deyi, GAN Wenyan ,et al. Study on formation control of multi-Robot systems[C]//Proc. Int. Conf. Intelligent Syst. Des. Eng. Appl,, January, 16- 18, 2013. Washington: IEEE Computer Society,2013:1335-1339.

[3] DURRANT-WHYTE Hugh, PAGAC Daniel, ROGERS Ben, et al. An autonomous straddle carrier for movement of shipping containers[J]. IEEE Robotics & Automation Magazine, 2007, 9: 14-23.

[4] ODHAMS A M C, ROEBUCK R L, JUJNOVICH B A, et al. Active steering of a tractor-semi-trailer[J]. Proc. of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2011, 225(7): 847- 869.

[5] WU Xing, SHEN Weiliang, LOU Peihuang, et al. An automated guided mechatronic tractor for path tracking of heavy-duty robotic vehicles[J]. Mechatronics, 2016, 35(5): 23-31.

[6] KATO K, INOUE K, ARAI T, et al. Cooperative control and force limitation for multiple robots in single object transportation[C]//Proc. of 27th Annual Conf. of IEEE Industrial Electronics Society, November 29 - December 2, 2001. Washington: IEEE Computer Society,2001:422-427.

[7] YANG Xin, WATANABE Keigo, KIGUCHI Izumi, et al. A decentralized control system for cooperative transportation by multiple non-holonomic mobile robots[J]. International Journal of Control, 2004, 10: 949-963.

[8] YUFKA A , OZKAN M. Formation-based control scheme for cooperative transportation by multiple mobile robots[J]. International Journal of Advanced Robotic Systems, 2015, 12(12):1-15.

[9] GHOMMAM J, MEHRJERDI H, SAAD M, et al. Formation path following control of unicycle -type mobile robots[J]. Robotics and Autonomous Systems, 2010, 58(5): 727-736.

[10] 武星, 楼佩煌, 杨雷. 基于视野状态分析的机器人路径跟踪智能预测控制[J]. 机器人, 2009, 31(4): 357-364.