双驱动伺服曲柄压力机协调控制方案分析
2018-03-05贾得山吴明亮张来喜
贾得山,吴明亮,张来喜
(兰州理工大学机电工程学院,甘肃 兰州 730050)
在金属成型加工领域,运用曲柄连杆式伺服压力机进行冲压成型加工是当前最主要的加工工艺之一,但由于受到伺服电机容量的制约,曲柄连杆式伺服压力机无法提供大吨位的冲压能力[1]。ABB公司与济南第二机床厂联合开发的交流伺服电机和普通交流异步电机混合驱动的伺服压力机将两台电机的动力合并后驱动曲柄滑块运动[2]。由于滑块在低速工作阶段的运动是依靠两台电机间的运动抵消实现,因而滑块的运动调节范围有限。日本网野公司推出的双电机双肘杆式伺服压力机用两台伺服电机分别通过蜗杆驱动同一涡轮,然后通过丝杠将涡轮的转动转换成冲压头的上下移动,以实现增力的效果[3]。这种压力机的传动链相对较长,压力机冲压频率低。
为了满足市场产品多样化的需求,使曲柄连杆式伺服压力机能够提供大吨位的冲压能力,降低压力机的造价,本文采用伺服电机直接驱动两台曲柄连杆式伺服压力机共同带动冲压头上下运动的方式建立了双驱动伺服曲柄压力机的虚拟样机,该压力机的左右机架对称,两台驱动电机独立控制,且冲压头平行度和下死点可以进行自动补偿。由于双驱动伺服曲柄压力机是一个多变量、强耦合、非线性的复杂机械系统[4],如果通过控制系统对实际样机进行测试,将消耗大量的财力和时间。因此在制造实际样机前先借助虚拟技术建立一个虚拟样机进行测试,以找到控制系统的不足之处并对其进行不断改进,这样可以大大缩短研发周期。运用ADAMS和MATLAB建立联合仿真系统,不仅能对双驱动伺服曲柄压力机的运动学和动力学进行仿真分析,而且可以通过联合仿真控制系统直观地观察控制效果,为实际样机的研制提供可靠依据。
1 双驱动伺服曲柄压力机建模
1.1 双驱动伺服曲柄压力机三维实体模型的建立
利用SolidWorks软件建立双驱动伺服曲柄压力机的三维实体模型,然后导入ADAMS软件中,为了更好地模拟实际系统,还需要设置每一个部件的材料、质量、转动惯量等相关属性,使虚拟样机和实际样机的物理特性基本相同。经合理简化后建立的双驱动伺服曲柄压力机的三维实体模型如图1所示。

图1 双驱动伺服曲柄压力机三维实体模型
1.2 双驱动伺服曲柄压力机数学模型的建立
双驱动伺服曲柄压力机是由两台伺服电机并联直接驱动曲柄连杆式伺服压力机,所以需要建立曲柄连杆式伺服压力机的数学模型。曲柄连杆式伺服压力机可以认为是一个曲柄滑块机构,如图2所示。
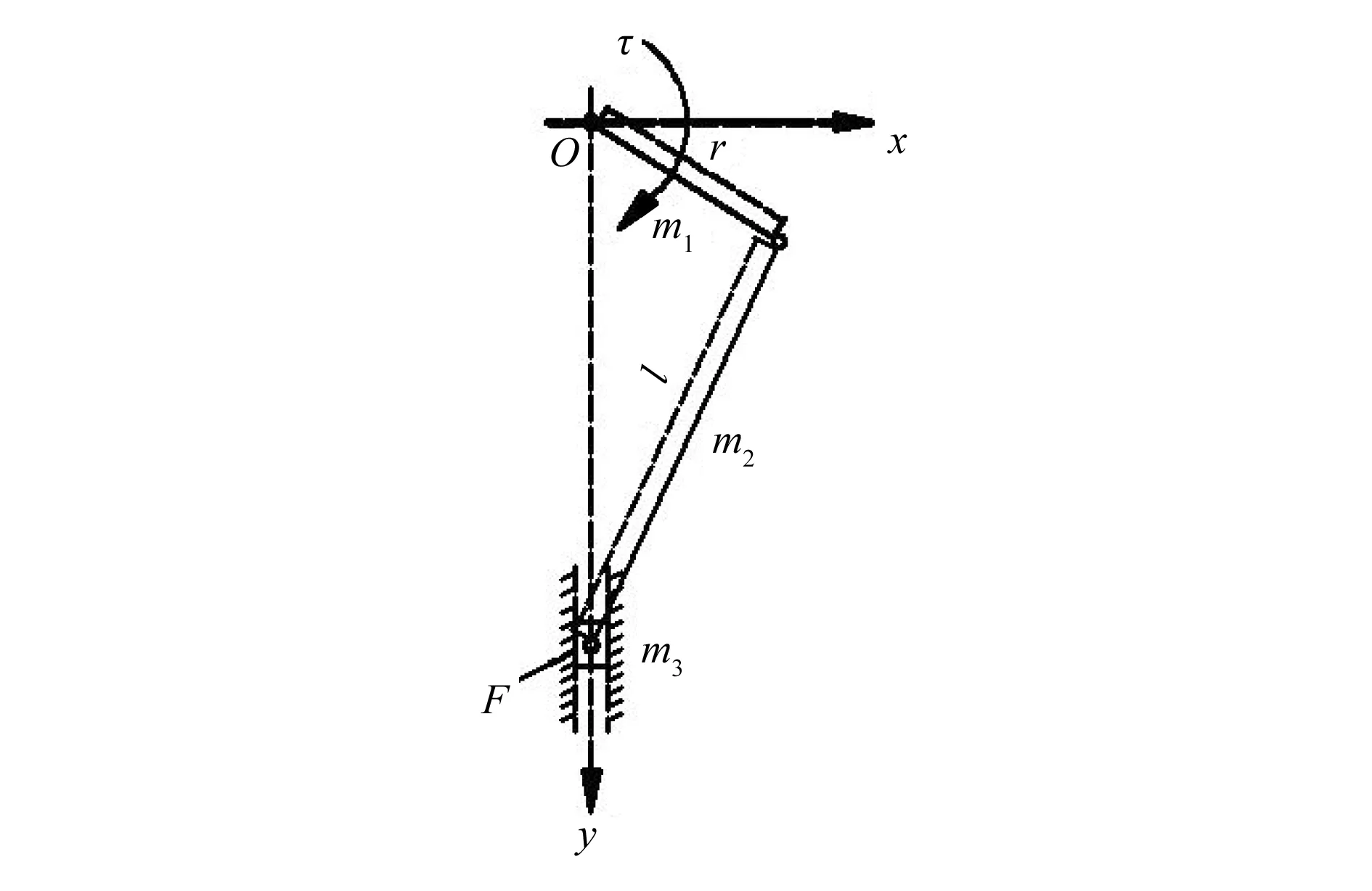
图2 曲柄滑块机构
运用拉格朗日方程建立压力机的数学模型,如式(1)~(7)所示。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
式中:r为曲柄长度;l为连杆长度;m1为曲柄质量;m2为连杆质量;m3为滑块质量;θ为曲柄转角;g为重力加速度;τ为驱动力矩;F为摩擦力;y为滑块位移。
1.3 双驱动伺服曲柄压力机数学模型的验证
数学模型的正确与否决定着所设计控制器的正确性。首先在ADAMS里对双驱动伺服曲柄压力机的三维模型进行运动学仿真,为了建立完整的运动学仿真模型,还需要对三维模型添加约束和驱动,添加约束和驱动的相关方法参见文献[5],首先在两个曲柄处分别添加15N·m的驱动力矩进行运动学仿真,然后根据建立的数学模型在MATLAB/Simulink模块中建立数值仿真系统进行仿真,仿真初始条件与ADAMS里的运动学仿真初始条件相同。
通过ADAMS的运动学仿真和MATLAB的数值仿真,分别得到了双驱动伺服曲柄压力机冲压头的位移、速度曲线图,如图3~图6所示。
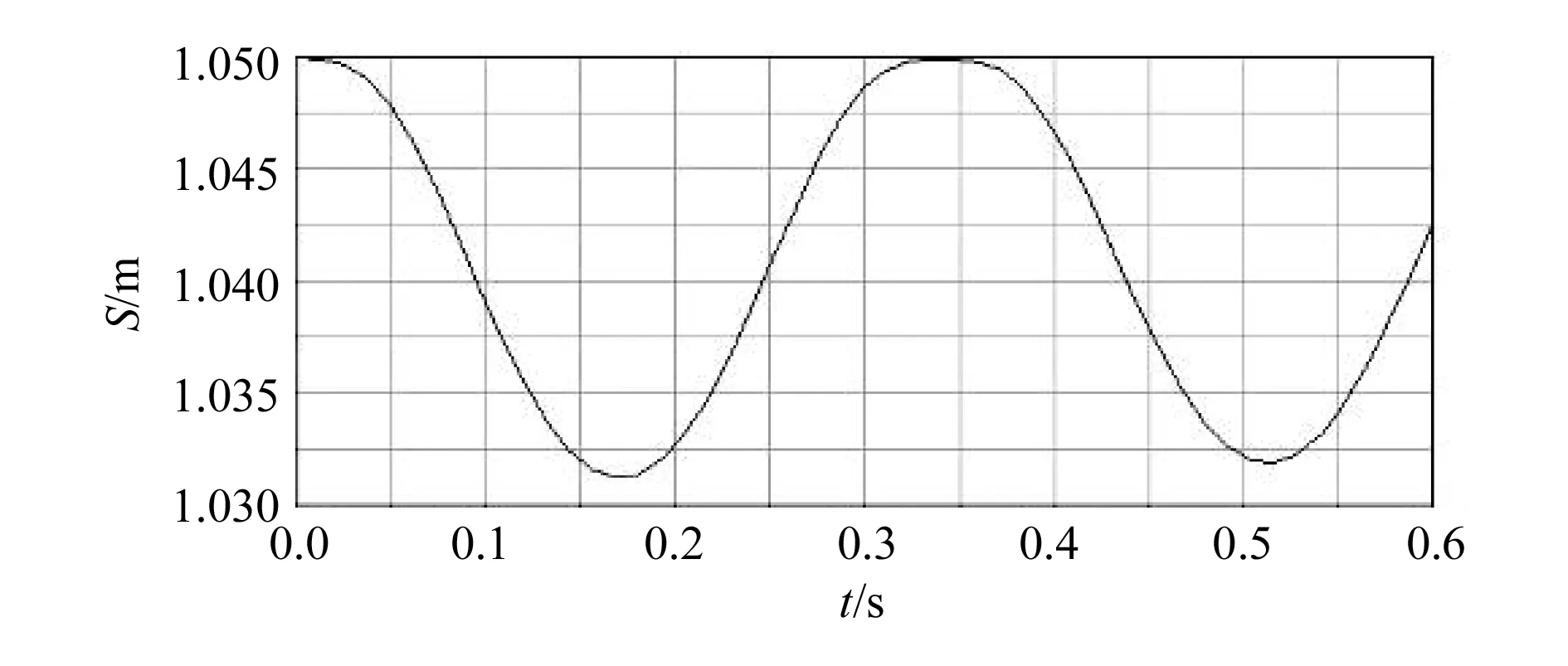
图3 ADAMS下冲压头位移图
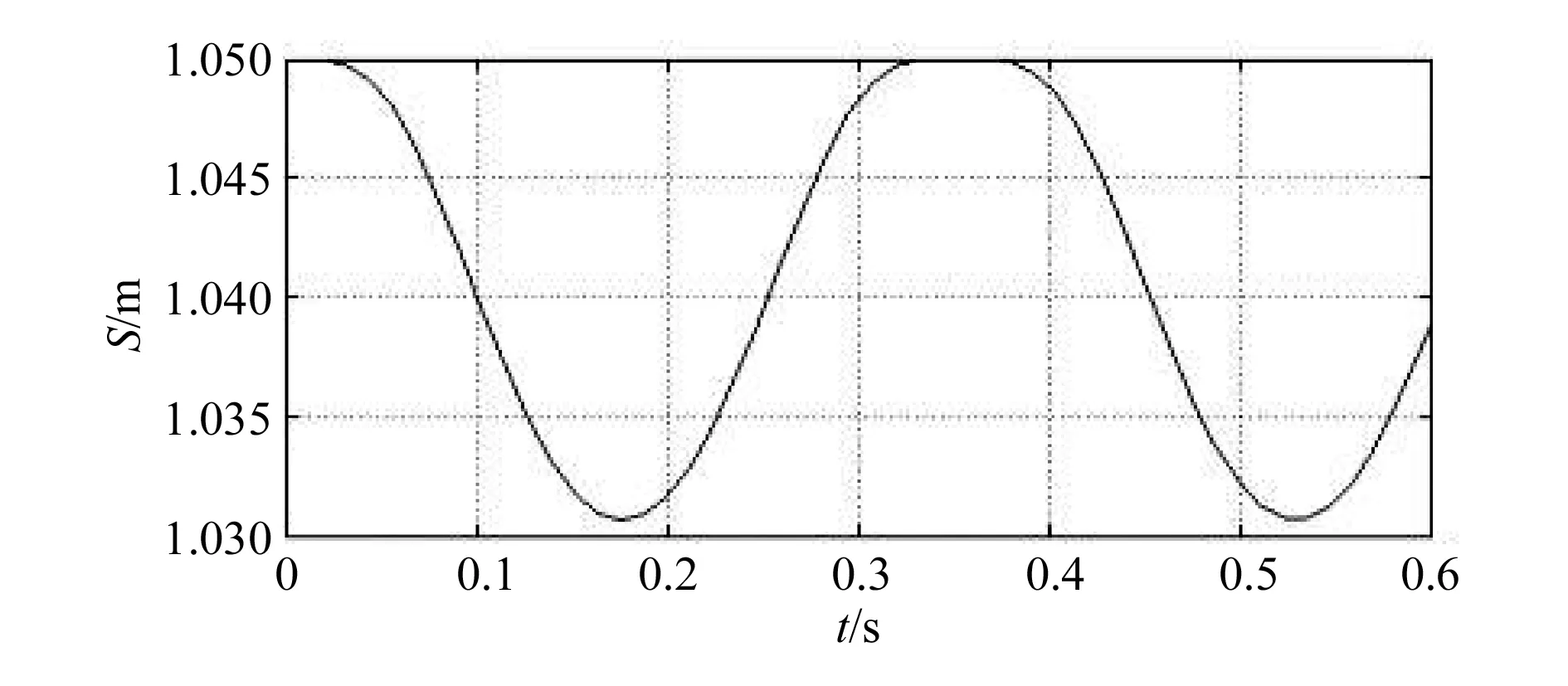
图5 MATLAB下冲压头位移图
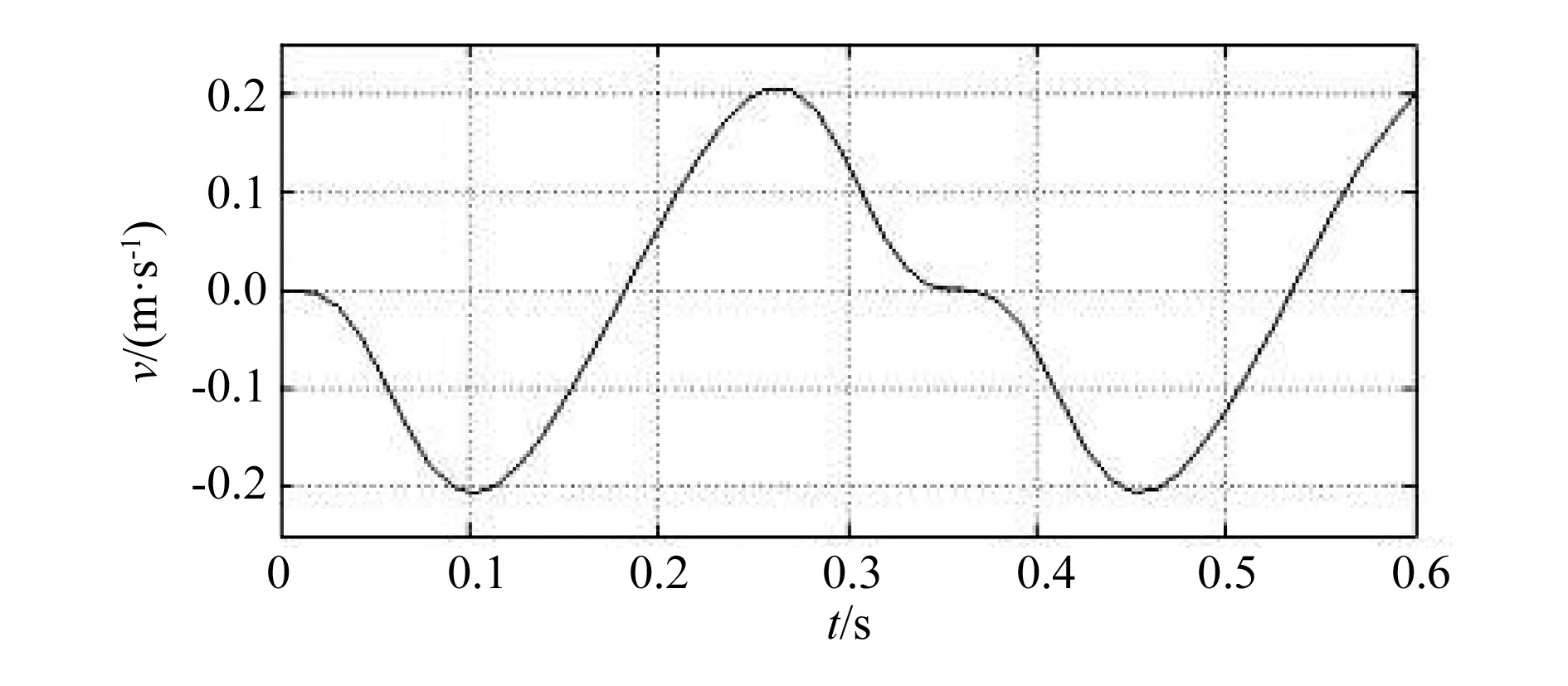
图6 MATLAB下冲压头速度图
分析仿真结果可知,所建立双驱动伺服曲柄压力机的数学模型是正确的。
2 双驱动伺服曲柄压力机控制系统的算法设计
双驱动伺服曲柄压力机采用两台曲柄连杆式伺服压力机共同带动冲压头上下运动的方式提供动力,两台电机独立控制且都由相应的伺服控制系统[6]控制,伺服控制系统的指令由一个上位机统一给定。各个伺服控制系统接收到由上位机通过高速同步串口传送的位置或速度指令后,控制电机驱动双驱动伺服曲柄压力机工作;同时,通过磁电编码器对整个控制系统进行位置反馈,以实现全闭环控制。传统的PID控制器容易受外来扰动和机械系统内部参数变化的影响,很难满足控制要求。针对双驱动曲柄伺服压力机的电机协调性问题,运用滑模变结构控制理论[7-9]设计控制器,其控制算法简单,不仅控制性能良好,而且对内部参数变化和外来干扰具有较强的鲁棒性。
2.1 滑模面的设计
取曲柄转角跟踪误差为:
e=θd-θ
(8)
(9)

定义滑模切换面为:

(10)
对滑模切换面求微分得:

(11)
2.2 滑模控制律的确定
指数趋近率不仅能够保证滑模到达条件,还可以通过合理选择趋近切换面的速率ε和指数项常数κ提高系统的鲁棒性,因此选择指数趋近率设计滑模控制器。
对于指数趋近率有:

(12)
由双驱动伺服曲柄压力机的数学模型式(1)可得:
(13)
联立式(8)~(13),可以求得系统的滑模控制律为:
(14)
2.3 稳定性分析
利用李亚普诺夫稳定性理论[10]进行稳定性分析,取李亚普诺夫函数为:
(15)
对式(15)求导得:
(16)
由式(16)可知,所设计的滑模变结构控制器满足稳定性要求。
3 联合仿真系统实验
3.1 联合仿真控制系统的建立
为了验证所设计控制器的效果,运用ADAMS和MATLAB做联合仿真。首先需要将ADAMS中已经建立好的双驱动伺服曲柄压力机模型导入MATLAB中,在MATLAB/Simulink主界面搭建联合仿真控制系统。
实际机械系统中,由于存在加工、制造、装配等误差,双驱动伺服曲柄压力机中与电机直接相连的两个曲柄和连杆质量不可能完全相同,而且两台电机由于各种内在和外在原因会出现不能同时启动的情况,为了能充分体现所设计控制器对双驱动伺服曲柄压力机的控制效果,将第二个控制器里曲柄和连杆的质量进行人为改变,并且将加到第二个控制器上的曲柄转角参考值信号延迟0.2s,联合仿真控制系统如图7所示。
3.2 联合仿真实验
根据已经建立好的联合仿真控制系统,通过给定参考信号来验证所设计控制器的效果。其中,双驱动伺服曲柄压力机的曲柄和连杆长度分别为100mm和950mm,曲柄质量分别为12.6kg和12.0kg,连杆质量分别为18.8kg和20.0kg,冲压头质量为42.93kg。图8、图9分别为采用PID控制器和滑模变结构控制器时双驱动伺服曲柄压力机两台电机的输入力矩误差曲线图。对比两图可以看出,采用滑模变结构控制算法的控制系统具有更好的抗干扰性和协调性。
采用滑模变结构控制算法时双驱动伺服曲柄压力机冲压头的位移、速度图分别如图10、图11所示。

图7 联合仿真控制系统图
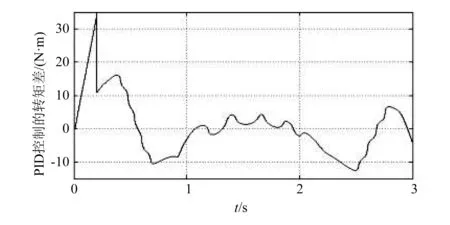
图8 采用PID控制算法时两台电机输入力矩误差曲线图

图9 采用滑模变结构控制算法时两台电机输入力矩误差曲线图

图10 冲压头位移图
通过对联合仿真实验的结果进行分析后发现,采用滑模变结构控制算法的协调控制系统具有较好的抗干扰性和协调性,并具有优于PID控制系统的性能,使得双驱动伺服曲柄压力机具有良好的动态响应特性。

图11 冲压头速度图
4 结束语
本文利用虚拟设计方法,实现了双驱动伺服曲柄压力机的本体以及控制系统的设计,大大提高了设计效率,为实际样机的开发节省了大量的时间和成本。
运用ADAMS和MATLAB软件,建立了双驱动伺服曲柄压力机的三维机械模型,在对其进行运动学和动力学仿真的基础上,搭建了基于ADAMS和MATLAB的联合仿真实验平台。通过联合仿真实验,验证了所设计滑模变结构控制器对双驱动伺服曲柄压力机协调控制的可行性,在仿真过程中得到的大量参数可以为实际样机的研制提供可靠的依据。所采用的分析设计方法,为双驱动伺服曲柄压力机的开发提供了一种新的思路,即在建立物理样机之前,充分利用虚拟样机技术,通过仿真分析对虚拟样机系统进行不断改进,以便得到最优的设计方案。
[1] 师后龙, 何光军, 鹿新建, 等. 曲柄压力机的传动系统及发展趋势[J]. 锻压装备与制造技术, 2010, 45(4):14-17.
[2] 赵升吨, 陈超, 崔敏超, 等. 交流伺服压力机的研究现状与发展趋势[J]. 锻压技术, 2015,40(2):1-7.
[3] 闵建成, 闫长海, 祁长洲, 等. 伺服压力机的特点与应用[J]. 金属加工(热加工), 2010 (23):6-10.
[4] 渠聚鑫, 夏琴香, 龙晓斌, 等. 伺服压力机主传动及其控制技术的研究进展[J]. 锻压技术, 2014(10):24-26.
[5] 于珊珊, 贺磊, 郭前建. 基于 ADAMS 软件的机械压力机工作机构优化设计[J]. 机械设计, 2013, 30(2):24-27.
[6] 李铁才. 伺服控制技术的应用发展[J]. 伺服控制, 2010 (3):34-36.
[7] HUNG J Y, GAO W, HUNG J C. Variable structure control: a survey[J]. Industrial Electronics, IEEE Transactions on, 1993, 40(1):2-22.
[8] DECARLOR, ZAK S H, MATTHEWS G P. Variable structure control of nonlinear multivariable systems: a tutorial[J]. Proceedings of the IEEE, 1988, 76(3):212-232.
[9] SABANOVIC A. Variable structure systems with sliding modes in motion control-a survey[J]. IEEE Transactions on Industrial Informatics, 2011, 2(7):212-223.
[10] MORENO J, OSORIO M. Strict Lyapunov functions for the super-twisting algorithm[J]. Automatic Control, IEEE Transactions on, 2012, 57(4):1035-1040.
