涌浪海域起重船运动响应特性与作业窗口分析
2018-03-05刘修成华晓涛杨秀礼
刘修成,华晓涛,杨秀礼
0 引言
在大型港口、桥梁建设以及海洋油气开发等领域,起重船都是必不可少的施工装备。随着施工水域逐渐由沿海遮蔽水域向外海开阔水域发展,波浪诱导船舶运动响应的现象日益凸显,尤其是周期性的横摇和纵摇运动会激发起重船吊钩吊物系统的空间受迫振动[1],这会对施工人员的人身安全构成威胁,同时也影响被吊物的安装精度。大型起重船“蓝疆号”在南海海区作业时,受波浪影响导致其海上作业待机率几乎超过50%[2]。因此,为合理安排施工期,保障现场施工安全与质量,有必要对其运动响应特性及作业窗口条件进行分析。
马尔代夫中马友谊大桥横跨Gaadhoo Koa海峡,该海域波浪以8~14 s长周期涌浪为主,主墩大直径钢护筒采用起重船配合液压冲击锤施沉。本文以施工中的一艏起重船为研究对象,从运动微分方程入手,采用数值计算得到横摇及纵摇的幅频响应特性,并引入ITTC标准海浪谱,得到运动响应谱能量密度函数,进而对运动幅值进行预测;施工期间,对桥址处的波浪以及起重船运动姿态进行实时观测,将运动响应实测值与理论方法得到的预测值进行对比;最后,结合现场吊装作业情况,采用统计的方法确定该起重船的作业窗口条件。
1 理论基础
1.1 运动受力分析
为了简化分析并得到船体的运动微分方程,在受力分析时作以下假定:假定船体为刚体;作用在船体上的是微幅规则波;运动幅值是微小的,一方面可认为是等体积倾斜,初稳性公式仍然适用,另外船舶在波浪中的受力和运动都可以作为线性问题处理。在以上假设的前提下,根据物体动平衡原理,得到波浪中船舶运动微分方程为[3]:

式中:准为横摇或是纵摇角;I忆为船舶自身惯性矩I与附加惯性矩J之和;N为运动阻尼系数;K为线性回复力系数;KL为钢缆的力矩系数;M(t)为波浪扰动力矩,其中钢缆力矩系数可由文献[4]的公式计算。
对于斜浪中的船体横摇和纵摇,需用斜浪中的遭遇周期以及相当波倾来替代横浪或是迎浪中的波浪周期和波倾。针对系泊状态下的工程船舶,斜浪中的遭遇周期等于波浪周期,采用相当波长替代实际波长计算有效波倾角。
综上,船体运动方程是一个二阶常系数非齐次微分方程式,可以通过4阶Runge-Kutta法求解得到船舶横摇和纵摇运动的频域响应函数。
1.2 不规则波中运动幅值预报
以上是规则波作用下船舶运动响应的求解过程,而自然条件下海浪一般是随机的、不规则的,因此引入波浪谱密度函数S(棕)来描述不规则波浪能量相对于频率的分布情况。考虑施工海域以涌浪为主,文中选用ITTC标准海浪谱作为参考,此海浪谱适用于充分发展的海浪,其一般形式如下:
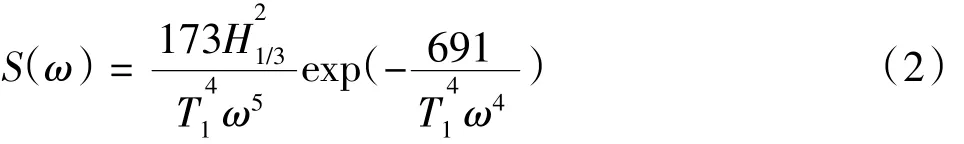
式中:H1/3为有义波高;T1为谱形心周期,与谱峰周期的关系为:Tp=1.282T1。
船体在海浪谱的作用下,运动响应谱SR(棕)等于与波浪谱S(棕)之间的关系如下:


式中:m0为运动响应谱的零阶矩。
2 工程实例分析
现以施工海域的一艘船长99.8 m、型宽32.2 m、型深8 m、设计吃水3.8 m,起吊能力为1 000 t的全回转起重船为研究对象,计算工况选取“起吊前、100%油水”工况。取船体中心为坐标原点,x轴正方向指向船首,y轴正方向垂直于纵中线的右手直角坐标系。
在施工期间,采用挪威Nortek公司坐底式波浪观测仪,设定每间隔0.5 h采集一定数量的波数,并分析得到桥址处波浪的有义波高、谱峰周期以及主浪向角等参数,波浪观测仪的安装位置见图1。与此同时,通过安装在起重船上的瑞典SMC公司船舶运动姿态传感器记录相应时间段(15~20 min)内船体运动情况。

图1 现场布置示意图Fig.1 Site layout diagrammatic sketch
2.1 幅频特性和幅值预报
该起重船的船体为非自航简易箱型方驳,型宽与吃水之比远远超过常规船型。为简化计算,忽略纵摇与升沉耦合运动的影响,采用数值方法求解运动微分方程的手段,分别得到起重船横摇、纵摇运动响应的幅频特性。将式(1)的运动微分方程作变换,设 准=x1,准觶=x2,得到可用于 Runge-Kutta法进行数值计算求解的方程如下:

在规则波波高为1 m,圆频率为0.4~2.2 rad/s,浪向分别为 0毅、30毅、45毅、60毅以及 90毅作用下,得到的单位波幅下船舶横摇、纵摇运动的频域响应以及有效波倾角随频率的变化曲线如图2所示。
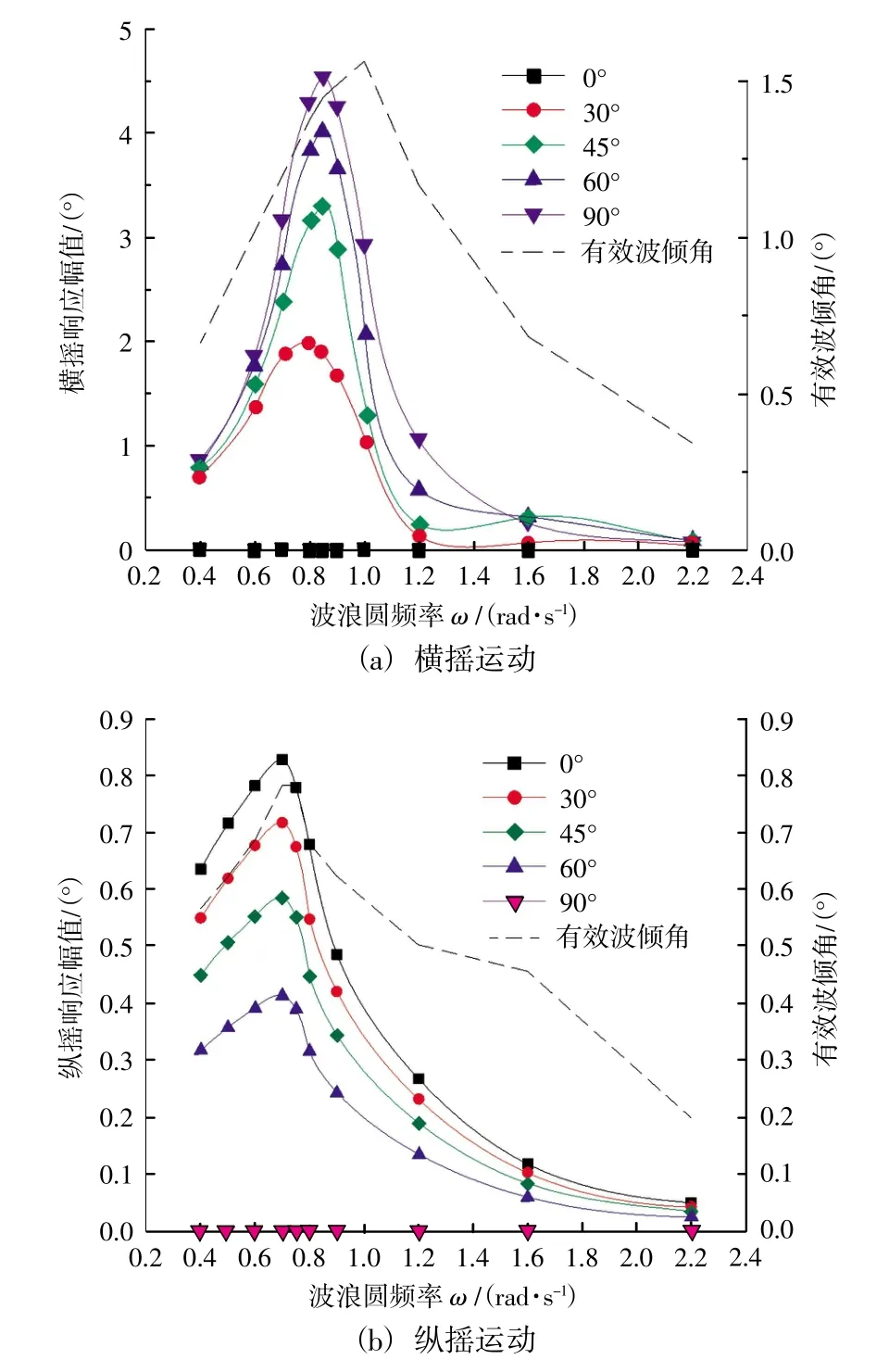
图2 船体运动响应幅值曲线Fig.2 Response amplitude curves of ship motions
由运动微分方程可知,在波浪作用下,船体自身相当于一个能量转换器,输入的是波浪有效波倾角,输出的是横摇、纵摇角。船体运动的幅值主要受波浪圆频率以及无因次衰减系数的影响。在波高、浪向一定的条件下,波长越长,有效波倾系数越趋近于1,而表面波倾角越小,横摇、纵摇运动所对应有效波倾角分别在1.0 rad/s及0.8 rad/s处取极大值,如图2中虚线所示。另外,当波浪频率与运动的固有频率接近时,会产生谐振现象,此时无因次衰减系数的影响占主导,无因次衰减系数值越小,谐振区运动幅值放大效应越明显,由图2可知,当波浪圆频率与船体横摇固有频率0.85 rad/s接近并产生谐摇现象,其横浪作用下横摇角响应幅值约为有效波倾角的3倍,而迎浪作用下谐振区纵摇角幅值约等于有效波倾角。总的来说,运动幅值频率响应曲线在固有频率附近取得极大值,远离谐振区,幅值显著减小;由于纵摇运动无因次衰减系数较大,同等条件波浪作用下,纵摇运动幅值明显要小。
得到了船舶在规则波作用下的横摇幅频特性后,引入有义波高为1 m的ITTC标准海浪谱,谱形心周期为4 s、6 s、8 s、10 s以及12 s。根据上述频谱分析得到的运动幅值响应算子,在海浪谱的作用下,由式(3)可以求得运动响应谱密度函数以及零阶矩m0,再通过式(4)得到不同谱峰周期及浪向角所对应的有义幅值见图3。

图3 运动响应实测值与预测值对比Fig.3 Comparison of measured and predicted motion amplitude
2.2 预测与实测结果对比
为了验证上述方法预测船体运动幅值的可靠性,采用运动姿态传感器记录起重船在非作业状态下的横摇、纵摇时间历程曲线,并统计分析得到运动有义幅值。该施工海域为印度洋涌浪海域,波浪仪观测到的谱峰周期一般集中在10~14 s,主浪向角与船体纵轴线的夹角在20毅~30毅范围变化,为方便对比,根据线性波理论,将不同有义波高所对应的运动幅值折算到单位波高作用下的结果,图3给出了不同谱峰周期及主浪向角所对应的横摇、纵摇幅值预测与23组实测值的对比。
由图3可知,在谱峰周期为10~14 s区间内,横摇角有义幅值随着谱峰周期远离谐振区而较小,数值计算预测值与实测值大小和趋势上吻合,个别存在偏差;而纵摇角有义幅值在谱峰周期为12 s左右达到极大值,实测值相对于预测值偏大。这与数值计算时仅考虑了波浪诱导船体运动这一主要因素的影响,而未考虑风、流以及潮汐等因素有关,另外计算纵摇时,忽略了升沉运动耦合项的影响。总的来说,在对非自航工程船舶运动响应评估时,可采用上述方法进行预测。
2.3 作业窗口条件分析
由于波浪诱导船体的摇荡运动,对于系泊状态下的工程船舶,横摇、纵摇以及升沉运动对施工作业影响较大,尤其是周期性的横摇和纵摇运动会激发吊钩吊物系统的受迫振动,当激励频率与吊钩吊物系统固有频率接近时,会出现较大振幅,对吊装控制产生极不利的影响,如现场起重船吊装液压冲击锤进行套锤作业时,锤体水平面内的摆动幅值达到8 m左右。为了保障现场人员和设备安全以及安装精度,需分析作业的窗口条件,用以指导施工。目前对于起重船的作业条件研究较少,也缺乏相关的规范依据,船长一般通过经验判断,或是等待“好窗口”才能进行吊装作业[6]。为了确定起重船的作业窗口,并及时捕捉能作业的“好窗口”,本项目通过高精度测量仪器实时监测施工海域的波浪数据以及船舶运动姿态。
起重船在方便现场作业的条件下,尽量采用顺浪向布置。图4给出了纵摇、升沉运动有义幅值与有效波高曲线。可以看出,在波浪主浪向角变化不大,谱峰周期集中在10~14 s的情况下,纵摇、升沉运动幅值随有义波高变化趋势明显;另外,经统计发现,当波高一定时,纵摇与升沉幅值之间存在线性关系,两者比值约为1.6。

图4 纵摇和升沉有义幅值与有效波高曲线Fig.4 Curves of pitch&heave amplitude and significant wave height
在以上分析的基础上,确定横摇、纵摇运动幅值边界条件即可以得到起重船正常作业窗口。本文对运动姿态传感器长期观测得到的作业与非作业时段横摇、纵摇有义幅值进行统计整理,得到作业与非作业工况船体横摇、纵摇运动散点图如图5所示。图中,“茵”、“伊”标识分别代表作业与非作业状态船体运动情况,可以清晰地看出,当横摇幅值大于0.6毅或纵摇幅值大于0.7毅时,吊装作业完全无法进行;当横摇幅值小于0.5毅且纵摇幅值小于0.55毅,起重船可以正常作业;其它情况得视被吊物的重量以及安装精度而定。得到横摇、纵摇幅值边界条件后,在谱峰周期为10~14 s,主浪向角变化不大的条件下,可推算出作业窗口期有义波高需小于0.75~0.8 m。确定此有效波高临界值,便可以通过波浪观测仪实时捕捉能够作业的波浪窗口,提高作业效率。
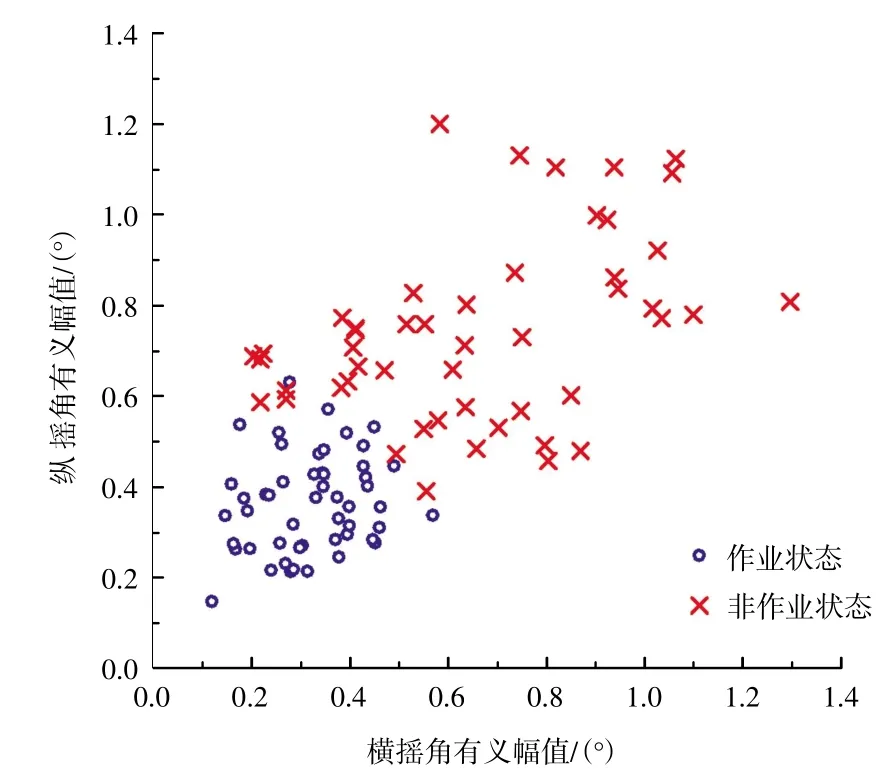
图5 作业与非作业状态下船体运动散点分布Fig.5 Scatter distribution of ship motion in operating and non-operating states
3 结语
本文研究了涌浪海域起重船横摇、纵摇运动特性,将数值方法求解结果与实测值进行对比,并统计起重船作业与非作业条件下运动幅值,得到以下结论:
1)采用运动微分方程数值求解船体运动响应时,需考虑有效波倾系数的影响,并选择合适的无因次衰减系数,这对运动幅值预报的准确性影响较大;对于非自航、以方型驳船为船体的工程船舶,计算纵摇幅值时,可参照横摇运动响应幅值的求解方法,忽略升沉运动耦合项的影响得到的结果与实测值相差不大。
2)在大量运动姿态监测数据的基础上,结合现场施工记录,采用统计的方法得到了涌浪海域起重船正常作业的运动临界值,并推算窗口期有义波高应小于0.75~0.8 m,为与本船主尺度相近的起重船作业条件的判定提供了依据。
[1] 董艳秋,韩光.起重船吊物系统在波浪中的动力响应[J].中国造船,1993(1):63-71.DONG Yan-qiu,HAN Guang.Dynamic response of lifting load system of crane vessel in waves[J].Shipbuilding of China,1993(1):63-71.
[2] 孟庆顺.大型起重工程船吊钩减摆系统的研究[D].哈尔滨:哈尔滨工业大学,2007.MENG Qing-shun.Development of anti-swing system for hook mounted on the large-size crane vessel[D].Harbin:Harbin Institute of Technology,2007.
[3] 盛振邦,刘应中.船舶原理(下)[M].上海:上海交通大学出版社,2004.SHENG Zhen-bang,LIU Ying-zhong.Ship principle(Part域)[M].Shanghai:Shanghai Jiao Tong University Press,2004.
[4] 王学亮.大型起重船在海浪中的运动响应研究[D].天津:天津大学,2003.WANG Xue-liang.Study on the wave-induced motion of the large derrick barge ships[D].Tianjin:Tianjin University,2003.
[5]KIM C H,HENRY C J,CHOU F.Hydrodynamic characteristics of prismatic barges[C]//Offshore technology conference.Houston,1971.
[6] 张志明,徐丹静,张超,等.大型起重船船型开发的若干技术问题初探[J].船舶,2005(1):10-15.ZHANG Zhi-ming,XU Dan-jing,ZHANG Chao,et al.Technical problems in ship type development of large crane ship[J].Ship&Boat,2005(1):10-15.
