天津黏土地基动载模式下的孔压发展规律

雷华阳，娄金峰，许英刚，刘英男

0 引言

随着经济建设的高速发展和城镇化水平的迅速提高，社会对交通运输的需求也越来越大，大量的交通基础设施建设方兴未艾，然而路基沉降以及不均匀沉降问题也日益突出。上海地铁1号线[1]在施工完成后未通车的2年多时间内沉降量为2~6 mm，但通车后在交通荷载下8个月内沉降就达到60 mm。交通荷载作用下，孔压的累积和消散使土颗粒间有效应力发生变化，导致土体变形和强度变化。因此，有必要探究出动孔压的发展规律，为科学设计施工、合理预测路基沉降提供支持。

土体在动力条件下的孔压发展规律要比在静力条件下复杂得多。在动载方面影响因素主要有振动频率、动载幅值、振动次数、加载波形等，在土体自身性质方面影响因素主要有应力历史、结构性、颗粒级配以及物理性质等，在试验条件方面有排水条件、固结度、固结应力比、静偏应力等因素影响。郑刚等[2]研究发现，振动频率对原状土的影响要大于重塑土，并且频率越低时原状土孔压上升越快。张涛[3]总结了近年来模拟交通荷载的试验条件，指出地铁列车荷载作用时没有拉应力，并通过对比认为偏压正弦波（即施加偏应力和正弦波荷载）能够更合理地模拟地铁列车荷载。丁智等[4]通过排水条件和不排水条件下的试验，得出两者的孔压关系，可通过不排水试验间接地获取排水条件下的孔压。魏新江等[5]认为，固结度越低的试样孔压发展越快，越先达到稳定，并且稳定时的孔压较大。王军等[6]对杭州饱和黏土进行了试验研究，认为土体进行各向异性固结时，由于初始静剪应力的存在会加速土体软化，并且其孔压变化缺乏一定规律性。霍海峰等[7]的试验研究结果表明，静偏应力对黏土动力特性影响显著，当静偏应力为0或为拉时，动孔压在-1~1 kPa之间波动。

天津紧邻渤海，地处海河下游，地质条件较为复杂，针对天津黏土动孔压发展规律的研究还较少。面对天津地区大量基础设施建设的需求以及安全质量标准的提高，亟需提出一个适用于天津地区的孔压发展模型。为此，本文以天津地区正常固结饱和黏土为研究对象，考虑动应力比、振动次数和结构性因素，开展黏土在动载作用下孔压特性的研究，为预测天津黏土在动载作用下的沉降提供支持。

1 试验方案

本试验原状土样取自天津站沿线，取土位置位于地面以下约10 m，其物理指标如表1所示。尽管原状土和重塑土在物理性质等方面差异较小，但在结构性方面有很大不同，因此本文利用重塑土试验与原状土作对比。

表1 土的物理参数Table 1 Physical parameters of soil

试验设备采用GDS动态三轴试验机，型号为ELDyn。根据李晓萍等[8]对天津地区土体物理力学性质的统计，天津地区黏土的侧压力系数K0在0.43~0.58之间，本试验取K0=0.5。固结轴向应力为100 kPa，有效固结应力p0为50 kPa。试验采用由应力控制的偏压正弦波进行加载，振动频率f取1 Hz，采用不排水条件，具体试验方案如表2所示。其中，动应力比子定义为滓d/2p0，滓d为动应力幅值。

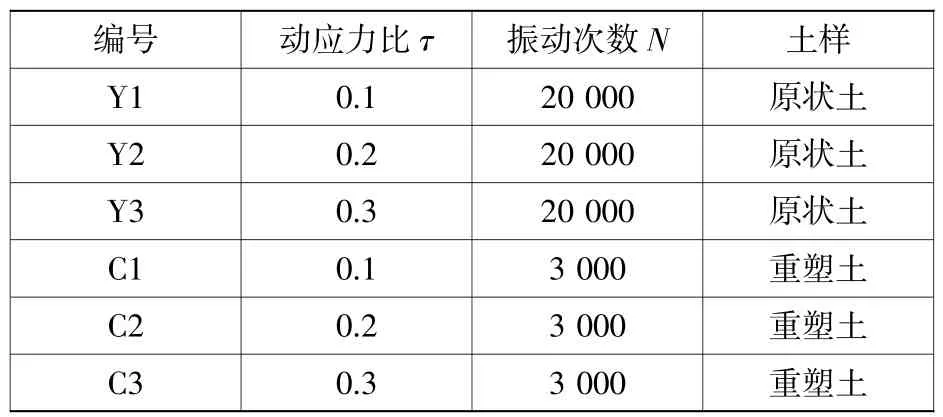
表2 动三轴试验方案Table 2 Scheme of dynamic triaxial test

2 试验结果分析

2.1 孔压发展规律

黏土在动载下的孔压以孔压归一值u*表示。u*定义为驻u/p0，驻u为孔压增量。

针对原状土，不同动应力比和振次条件下孔压发展有所不同。由图1可得，在相同动应力比条件下，孔压增长速率随着振次的增加而减小。孔压增量由两部分组成：一部分是由于动载作用于孔隙水直接产生，另一部分是由于土体变形、孔隙体积压缩产生。振动初期，土体变形较快，孔隙体积迅速压缩，孔压上升较快。当土体更加密实后，孔隙体积变化很小甚至不再变化，孔压上升速率逐渐减慢。图2显示振次一定时，孔压随动应力比的增大而增大。动应力比较小时，孔压随动应力比增长较慢；动应力比较大时，孔压随动应力比增长较快。

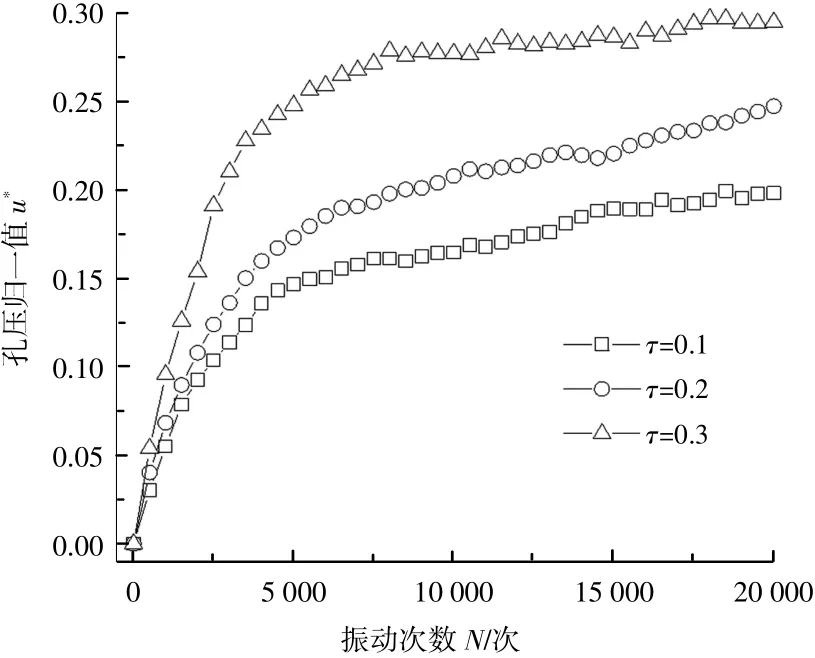
图1 原状土孔压随振动次数变化图Fig.1 Variationdiagramoftheporepressureofundisturbed soil with the number of vibrations

图2 原状土孔压随动应力比变化图Fig.2 Variationdiagramoftheporepressureofundisturbed soil with the dynamic stress ratio

针对重塑土，孔压发展与原状土有较大不同。由图3可得，重塑土孔压在初期迅速上升，达到极限值后稳定，并且达到稳定所需的振次较少，从试验结果中可看出仅需约750次即可达到稳定。孔压在稳定后会有略微的下降，在动载下重塑土土颗粒迅速发生重新排列而达到较密实的状态，此时孔压下降说明土体发生了轻微的剪胀现象。重塑土孔压发展都比较大，孔压稳定时u*在0.75~0.85之间。由图4可得出，当动应力比增大时，孔压发展的整体趋势为逐渐增大，但没有出现动应力比越大孔压增长越快的现象。

对比原状土和重塑土的试验结果可看出，重塑土孔压上升速率比原状土大很多，这恰恰体现了结构性对孔压发展的影响。重塑土结构性较差，颗粒间联结作用较弱，土颗粒更容易发生重新排列。在动载作用下，重塑土骨架迅速发生变形，被压缩的孔隙体积较大，导致孔压上升速率较大，当土体达到较密实的状态时孔压即进入平稳阶段。原状土土颗粒间有一定程度的粒间联结，土骨架可承担一部分动载，土体变形比重塑土小，被压缩孔隙体积相对较小，孔压上升速率较小。

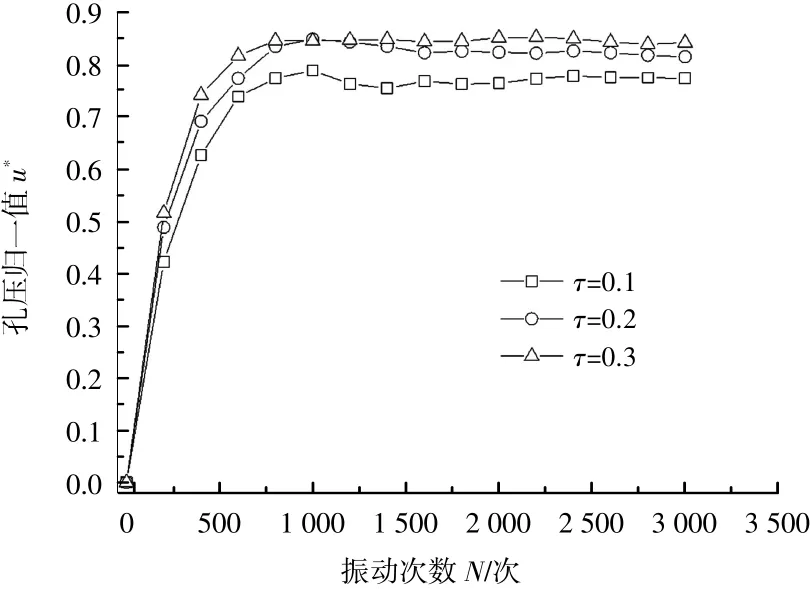
图3 重塑土孔压随振动次数变化图Fig.3 Variation diagram of the pore pressure of remolded soil with the number of vibrations

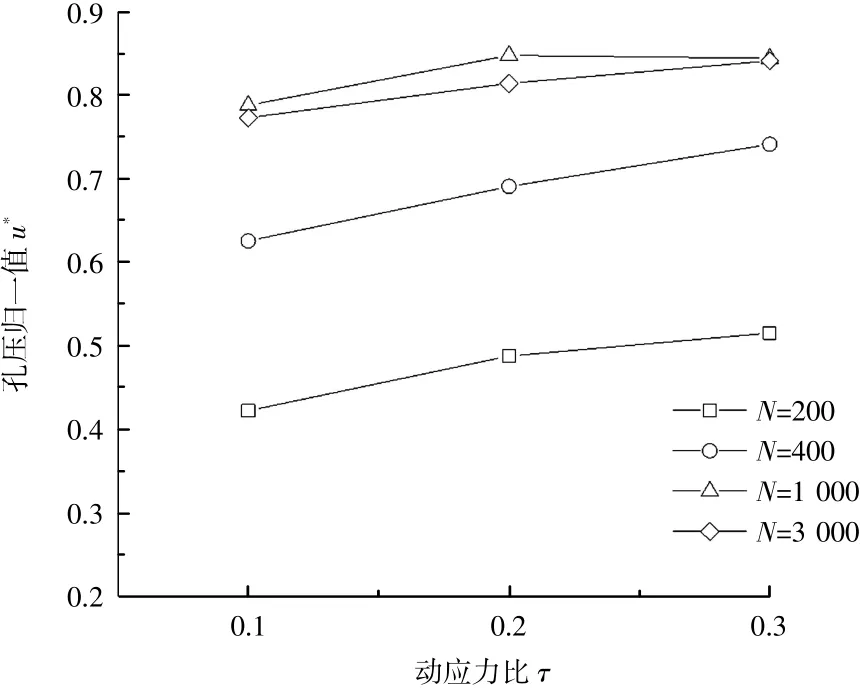
图4 重塑土孔压随动应力比变化图Fig.4 Variation diagram of the pore pressure of remolded soil with the dynamic stress ratio

2.2 孔压模型的建立

对于不同的试验，振动次数N是一个客观的变量，不随其他变量的变化而变化，因此选用N作为孔压模型的主要变量。根据本文试验的孔压发展规律，采用双曲线型孔压发展模型：

式中：A和B为反映动应力比子对孔压发展影响的参数，可用关于子的多项式表示，多项式次数越高拟合效果就越好，但同时也会增加参数数量。考虑拟合效果、减少参数等因素，A、B分别表示为 A=a+b伊子+c伊子2和 B=d+e伊子，a、b、c、d、e为参数。将A、B代入到式（1）中即得到本文所建立的孔压发展模型：

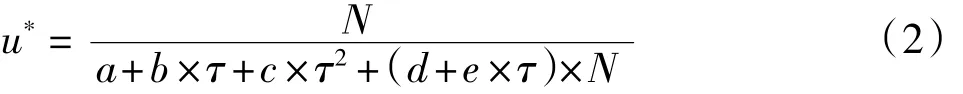
根据式（2）对原状土试验结果进行拟合，图5为拟合结果，拟合参数如表3所示，拟合相关系数R2均在0.98以上。图6显示了子为0.3时，将周建[9]提出的对数型模型、叶俊能等[10]提出的幂函数型模型与本文的双曲线型模型进行对比，相关模型及R2如表4所示。可看出，对数型模型在初期增长过快，幂函数型模型在后期孔压不能很好地收敛，仍以较快的速度增长。相比之下，本文的双曲线型模型则可更好地表示孔压的发展。

图5 原状土孔压发展拟合结果Fig.5 Fitting results of pore pressure of undisturbed soil

表3 孔压模型参数Table 3 Parameters of pore pressure model

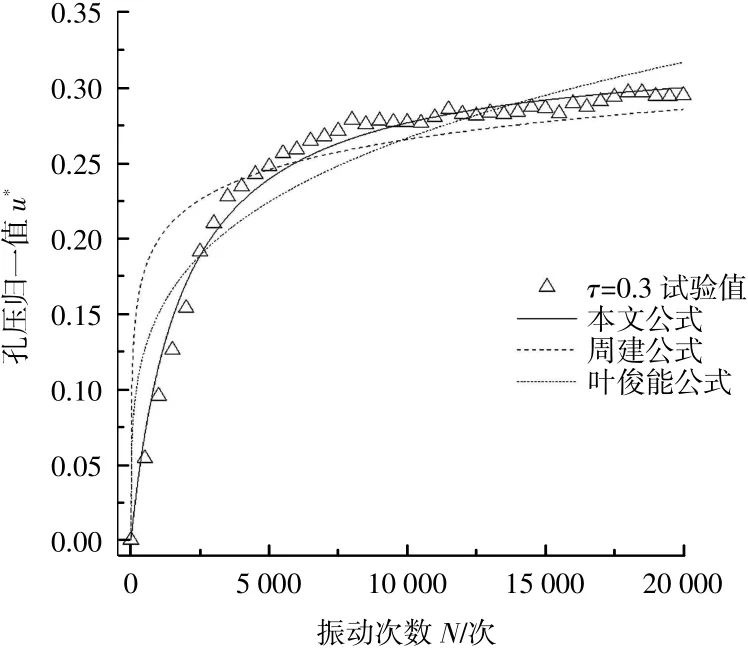
图6 不同孔压发展模型拟合比较（子=0.3）Fig.6 Fitting comparison among different pore pressure models(子=0.3)

表4 不同孔压模型及其拟合相关系数Table 4 Different pore pressure models and their fitting correlation coefficients

3 孔压模型的应用

3.1 沉降计算方法

黏土路基的沉降可以分为两个部分[11]。其中一部分是在不排水条件下累积塑性变形所产生的压缩沉降S1，另一部分是土体累积的孔压消散时所产生的固结沉降S2。建立孔压模型主要是为了预测第二部分的土体沉降。在预测黏土长期沉降时，可遵循以下步骤：

1）首先确定土体的应力场分布。所需确定的应力场包括由土体自重、静偏应力、动载产生应力场的叠加。

2）计算得出S1。根据不排水三轴试验得到的应变试验结果，用经验公式来拟合可得到土体累积塑性应变发展模型。结合分层总和法，按照式（3）计算得到 S1：

式中：着i为动载引起的累积压缩应变，可根据应变发展模型确定。

3）计算得出S2。与应变相同，通过动三轴试验得到孔压发展模型。近似以每层中心处的孔压值作为该层的孔压值，根据太沙基一维固结理论，S2可由式（4）确定：

式中：mvi为体积压缩系数；ui为动载下不排水所累积的孔压值，可根据孔压发展模型确定；Ui为固结度，实际计算时可以保守地认为固结度为100%。

4）将计算出的S1和S2相加，即为土体最终沉降S。

3.2 列车荷载下黏土路基长期沉降预测

天津某铁路工程建设场地土层基本参数如表5所示，地下水位为地表以下0.5 m处。由于土质条件、应力状态等沿长度方向变化不大，可简化为平面应变问题。火车引起的应力可简化为作用在路基面处的均布条形荷载，通过计算得到铁轨中心线下不同深度的附加应力，将其作为土体上的动应力。路基面处动应力经验公式为：

式中：P为火车静轴重，V为火车速度。取火车静轴重为20 t，速度为80 km/h，则火车轨道下路基面处动应力为69 kPa。每年振动次数取为200 000次。其计算模型示意图如图7所示。由于试验时黏土应变随振次的变化曲线形状与孔压随振次变化曲线形状类似，因此采用与孔压相同的拟合公式对应变试验结果进行拟合，得到应变发展模型。利用应变发展模型和孔压发展模型，根据式（3）和式（4）即可对沉降进行预测。

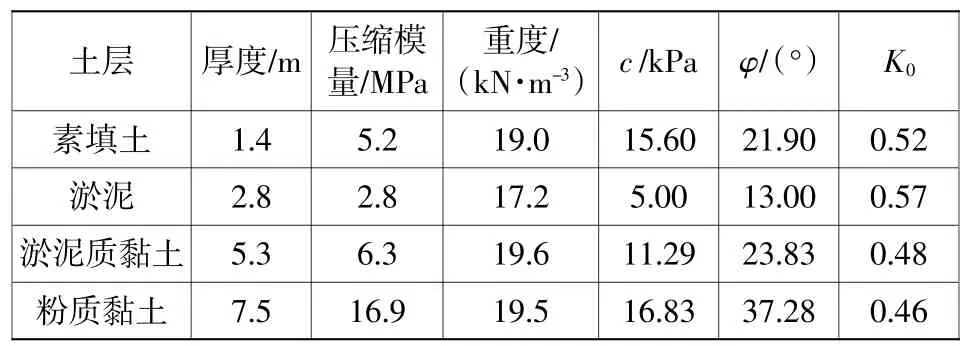
表5 土层基本参数Table 5 Parameters of soil layer

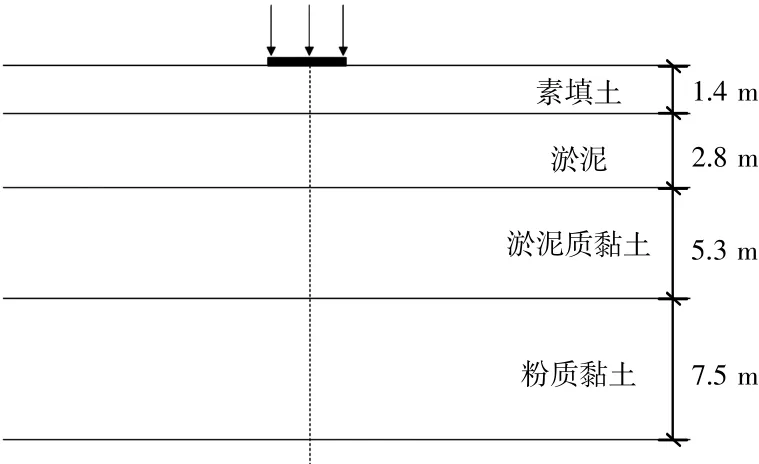
图7 计算模型示意图Fig.7 Schematic diagram of the computational model

根据上述方法，可以得到计算范围内任意时间、任意深度内产生的压缩沉降S1、固结沉降S2以及总沉降S。当压缩层厚度为9.5 m时，通过分层总和法计算得到不同时间内的累积沉降值，如图8所示。从图中可得，在动载下土体长期沉降主要发生在通车后约5 a内，5 a后产生的沉降较小。图9为不同时间条件下总沉降随压缩层深度变化曲线。从图中可得，沉降主要发生在地表以下7 m内，7 m以下土体产生的沉降较小。这些结论对预测和控制长期沉降都具有重要意义。

图8 压缩层为9.5 m时沉降随时间变化曲线Fig.8 Curve of settlement over time when the compression layer is 9.5 m

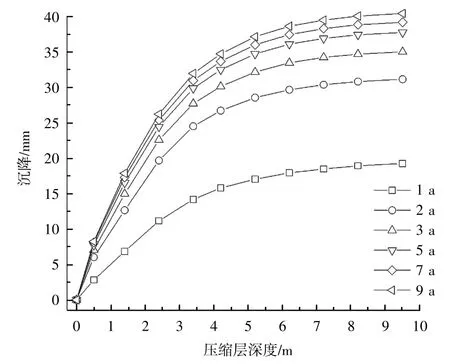
图9 不同时间条件下总沉降随压缩层深度变化曲线Fig.9 Curve of the total settlement over the thickness of the compressed layer under different time conditions

4 结语

本文通过动三轴试验对天津地区黏土孔压发展规律进行了研究，主要结论如下：

1）在不排水条件下，原状土孔压随着振动次数和动应力比的增大而增大，孔压增长速率随着振动次数的增加而逐渐减小，随着动应力比的增加而增大。

2）重塑土由于结构性较差，仅需很少的振动次数即可达到孔压稳定值，并且稳定值较大。稳定后孔压会有略微的下降，土体发生轻微的剪胀现象。

3）针对原状土试验结果，考虑动应力比和振动次数的因素，提出双曲线型孔压发展模型，能较好地模拟天津地区饱和黏土孔压发展。

4）黏土的长期沉降可分为不排水条件下累积塑性变形所产生的压缩沉降和土体累积的孔压消散时所产生的固结沉降，可根据动三轴试验结果建立应变和孔压发展模型预测，为工程实际决策提供支持。

[1]罗启洋.低频循环荷载下饱和软土的动力特性研究[D].广州：广东工业大学，2016.LUO Qi-yang.Research on mechanical response characteristic of saturated muck soil under cyclic loading of low frequency[D].Guangzhou:Guangdong University of Technology,2016.

[2] 郑刚，霍海峰，雷华阳，等.振动频率对饱和黏土动力特性的影响[J].天津大学学报，2013（1）：38-43.ZHENG Gang,HUO Hai-feng,LEI Hua-yang,et al.Contrastive study on the dynamic characteristics of saturated clay in different vibration frequencies[J].Journal of Tianjin University,2013(1):38-43.

[3] 张涛.地铁列车荷载下不同固结度重塑黏土动力特性试验研究[D].杭州：浙江大学，2014.ZHANG Tao.Experimental study on dynamic characteristic of remolded clay with different consolidation degree under subway loading[D].Hangzhou:Zhejiang University,2014.

[4] 丁智，张涛，魏新江，等.排水条件对不同固结度软黏土动力特性影响试验研究[J].岩土工程学报，2015（5）：893-899.DING Zhi,ZHANG Tao,WEI Xin-jiang,et al.Experimental study on effect of different drainage conditions on dynamic characteristics of soft clay under different degrees of consolidation[J].Chinese Journal of Geotechnical Engineering,2015(5):893-899.

[5] 魏新江，张涛，丁智，等.地铁荷载下不同固结度软黏土的孔压试验模型[J].岩土力学，2014（10）：2 761-2 768.WEI Xin-jiang,ZHANG Tao,DING Zhi,et al.Experimental study of pore pressure model of soft clay with different consolidation degreesundersubwayloading[J].RockandSoilMechanics,2014(10):2761-2 768.

[6] 王军，丁光亚，潘晓东.各向异性固结软黏土的循环软化-孔压模型[J].哈尔滨工业大学学报，2009（12）：166-170.WANG Jun,DING Guang-ya,PAN Xiao-dong.Cyclic-degrada原tion-pore pressure generation model for anisotropic consolidated clay[J].Journal of Harbin Institute of Technology,2009(12):166-170.

[7] 霍海峰，雷华阳.静动应力下正常固结黏土循环特性研究[J].岩石力学与工程学报，2015（6）：1 288-1 294.HUO Hai-feng,LEI Hua-yang.Cyclic properties of normal consol原idated clay under coupled effect of static and dynamic stresses[J].ChineseJournalofRockMechanicsandEngineering,2015(6):1288-1 294.

[8] 李晓萍，赵亚品.静止侧压力系数及其试验方法的探讨[J].铁道工程学报，2007，24（8）：20-22.LI Xiao-ping,ZHAO Ya-pin.Discussion on the still lateral pres原sure coefficient and testing method[J].Journal of Railway Engineering Society,2007,24(8):20-22.

[9]周建.循环荷载作用下饱和软黏土的孔压模型[J].工程勘察，2000（4）：7-9，43.ZHOU Jian.Pore pressure model of saturated soft clay under circu原lating load[J].Geotechnical Investigation&Surveying,2000(4):7-9,43.

[10]叶俊能，陈斌.海相沉积软土动强度与孔压特性试验研究[J].岩土力学，2011（S1）：55-60.YE Jun-neng,CHEN Bin.Dynamic strength and pore pressure property of marine deposit soft clay[J].Rock and Soil Mechanics,2011(S1):55-60.

[11]姚兆明，张明慧，陈军浩.饱和软黏土循环累积孔压模型及地铁隧道路基长期沉降计算[J].铁道学报，2012（9）：87-92.YAO Zhao-ming,ZHANG Ming-hui,CHEN Jun-hao.Cylic accu原mulative pore pressure explicit model of saturated soft clay and long-term settlement calculation of subway tunnel roadbed[J].Journal of the China Railway Society,2012(9):87-92.