海上风电复合筒型基础抗波浪液化研究
2018-03-05邓斌张金凤王利华
邓斌,张金凤,王利华
1 研究背景
近些年来,风能发电得到了越来越多的发展。但是海上风电基础周围的海床在波浪循环荷载作用下,可能会发生液化现象,危及上部结构物的安全。因此,波浪作用下的海床抗液化措施的研究不可忽视。
许多学者对海床抗液化措施进行了物理模型和数值模拟研究。Madabhushi[1]通过动态离心机建模,分别研究土壤致密化、排水管和土壤灌浆的方法来增强土体液化抗性。Sumer[2-3]等通过实验发现,用覆盖块石来增加波浪作用下的海床抗液化强度主要取决于块石的厚度和覆盖块石的孔隙率,并且用水槽实验研究了液化回填土中岩石护坡的稳定性。Susana和Rafeal[4]通过有限元模型研究表明密实法能有效地加强土体抗液化能力,减缓地基沉降。
复合筒型风电基础周围土体的动力响应也逐渐有学者开始研究。肖金龙等[5]研究了海上风电复合筒型结构周围土体动力响应,但结构物与土体接触上采用的是完全粘结接触,对真实情况的模拟不足。于聪等[6]利用OpenFOAM和有限元软件ABAQUS耦合,建立风电基础周围海床动力响应模型,但模型只将波压传递给土体,没有实现对波浪与土体相互作用的模拟。
本文将采用基于开源软件OpenFOAM建立的CFD-CSD耦合模型[7],求解波浪作用下海床动力响应及波浪-结构物-海床相互作用(Wave-Structure-Seabed Interaction,简称WSSI)的问题,来研究上覆块石对海床土体的抗液化效果。
2 模型设置
本文采用陈宝清等[7]基于OpenFOAM中的两相流模型和Biot固结方程建立的CFD-CSD耦合模型,且在两相流模型中添加源项进行造波。其中CFD模型控制方程采用RANS方程,并采用VOF法捕捉水体自由表面,CSD控制方程为Biot固结方程,模型已得到了很好的验证。本文将采用CSD-CFD耦合模型建立海上风电复合筒型基础周围的海床动力响应模型,分析基础周围海床在波浪力作用下的动力响应,来研究上覆块石对海上风电基础周围海床的抗液化效果。
2.1 数值模型参数设置
波浪数值模型采用的波浪及水深条件为江苏省盐城市响水地区风电机组项目实际情况的水文条件;波高采用50 a一遇有效波高3.26 m,平均周期8.58 s,波长87.24 m,极端高水位2.28 m。
根据以上波浪及水深条件,波浪数值水槽的具体设置如下:造波中心位于水槽左侧2.5倍波长即2.5L=218.1 m处,造波区为1倍波长即87.24 m;水槽左侧2倍波长区域为消波区,以消除边壁反射波对水槽内波浪稳定性的影响,提高模拟精度;同理,水槽右侧2倍消波区;风电基础应位于距造波区一定距离波浪稳定处,设于距水槽左侧500 m处。
水槽宽度应为风电基础宽度加上一定富裕宽度,以减弱边壁波浪反射对于水槽内波浪的影响,取为60 m。风电基础应相对于水槽宽度对称布置,即风电基础中心坐标为(500,15,30)。具体见图 1。

图1 数值模型示意图Fig.1 Schematic diagram of the numerical model
海床土体长度方向取为200 m,对称于风电基础处布置。高度方向为风电基础下部薄壁筒体的高度加上一定的富裕高度,取为15 m,宽度方向取水槽宽度60 m。取第1层粉土参数代表全部土体参数,且将土体设为各向同性,以垂向渗透系数代表土体渗透系数。
为研究块石层堆积厚度和堆积密度对抗液化效果的影响,土体和块石的参数设置参考Sumer[2]的物理实验设置,本文设置了3组不同的算例,具体设置见表1。

表1 海床土体和上覆块石的参数Table 1 Parameters of soil and stone of seabed
2.2 网格划分
先采用ICEM CFD网格“自上而下”(Up Bottom)的画法,以及2D-Block沿法向均匀拉伸变为3D-Block法分别建立水槽和土体网格。再使用snappyHexMesh将风电基础导入水槽和海床模型,并在海床土体模型基础上设置块石层区域,如图2所示。围绕风电基础外缘铺设5 m宽块石层,图中环形填充区域为块石覆盖区域,块石层为孔隙结构参与计算。

图2 模型网格示意图Fig.2 Schematic diagram of the model grid
3 海床动力响应分析
本文选取Ye[8]判别标准判断海床的液化情况。Ye给出了考虑土体黏聚力及库伦摩擦的液化判别标准:

式中:滓z忆、滓x忆、滓y忆为总有效应力分量,包括初始有效应力和由波浪引起的动有效应力,即滓z忆=滓z0忆+滓zd忆;c表示土体黏聚力;渍为土颗粒内摩擦角;u(x)为单位阶梯函数,即当 x逸0 时,u(x)=1,当 x<0 时,u(x)=0。式(1)中加入 u(x)函数的物理意义为:当土颗粒在水平方向不受压时,库伦摩擦及黏聚力对抗液化的贡献为0。由于波浪导致的海床液化多发生于波谷下方,故本文选取B、C、D三个测点(位置见图2)在波谷作用下的动力响应情况进行分析,并将其和未铺设块石层情况进行对比。本节给出B测点的结果如图3和图4所示,图3给出了B测点在不同算例下的超静孔隙水压力分布情况,图4给出了B测点在不同算例下竖向动有效应力分布情况。
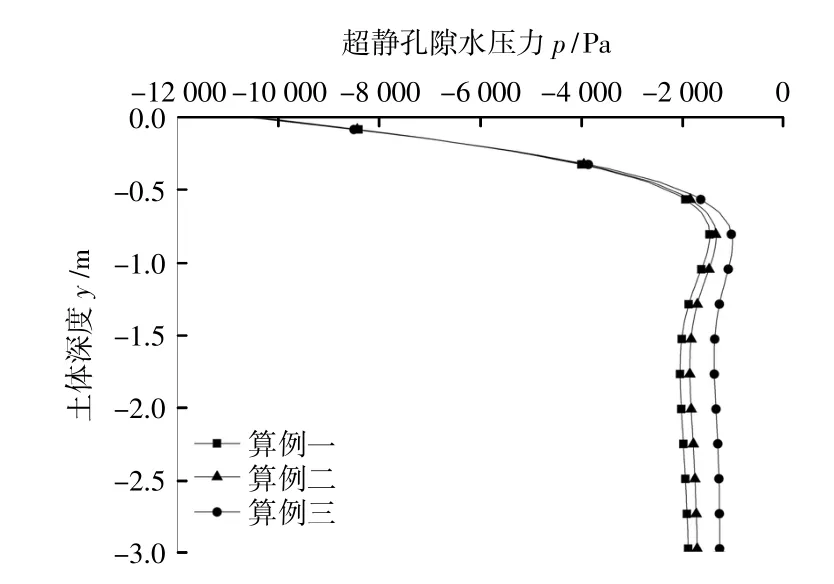
图3 测点B超静孔隙水压力垂向分布Fig.3 Vertical distribution of excess pore-water pressure at point B

图4 测点B竖向动有效应力垂向分布Fig.4 Vertical distributions of dynamic effective stress in Y-direction at point B
各测点超静孔隙水压力垂向上的分布都是在土体表层附近快速衰减,然后达到-0.8 m深度后趋于稳定,其中测点B处超静孔隙水压力衰减幅度最大(如图3所示),即风电基础迎浪侧。但各测点在铺设块石前后差异不大,铺设块石后孔隙水压力的衰减速度略有增加,算例2略小于算例3,而海床表面超静孔隙水压力在铺设块石前后基本无变化。可见,铺设块石层抗液化的原理只在于提高超静孔隙水压力的衰减速率。
各测点竖向动有效应力的整体趋势都是在土体表层附近快速增加,然后在-0.8 m深度后趋于定值,其中测点B处竖向动有效应力增加值最大(如图4所示)。各测点在铺设块石前后竖向动有效应力有明显减小,相比于不覆盖块石的算例1,算例2中竖向动有效应力最大值减小约900 Pa,算例3中减小约3 000 Pa。竖向动有效应力在铺设块石前后有明显变化,可推知铺设块石抗液化原理在于改善波浪作用下海床土体有效应力分布情况。一方面是通过增加了初始有效应力从而增加了土体强度,另一方面是减小了由波浪荷载产生的动有效应力。
4 最大液化深度分析
参照韩涛等[9]分析海床最大液化深度的方法,最大液化深度计算公式为 zlc= 渣-p0/酌忆s渣,其中p0为作用在波浪表面的动水压力,酌忆s为土的浮重度。
图5~图8给出了算例3在不同时刻下海床的最大液化深度分布。其中,t0为波峰到达测点A(见图2)的时刻,图中虚线圈为风电基础外边缘,实线圈为块石层外边缘。

图5 在t=t0时刻作用下海床液化分布(算例3)Fig.5 Liquefactiondistribution of the seabedat t=t0(test 3)

图6 在t=t0+T/4时刻作用下海床最大液化深度分布(算例3)Fig.6 Maximum liquefaction distribution of the seabed at t=t0+T/4(test 3)

图7 在t=t0+T/2时刻作用下海床最大液化深度分布(算例3)Fig.7 Maximum liquefaction distribution of the seabed at t=t0+T/2(test 3)
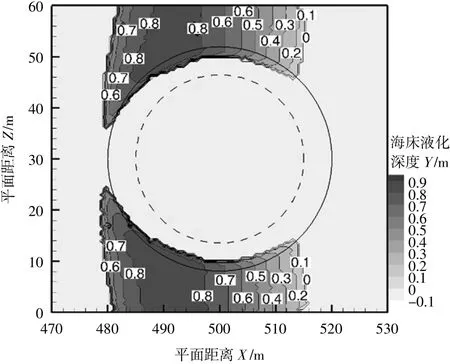
图8 在t=t0+3T/4时刻作用下海床最大液化深度分布(算例3)Fig.8 Maximum liquefaction distribution of the seabed at t=t0+3T/4(test 3)
海床仅在波谷作用区域液化,在单个波谷作用范围下发生液化的土体宽度约为30 m。对比抗液化措施前后,算例1块石覆盖区域的迎浪侧最大液化深度0.9 m,背浪侧最大液化深度0.9 m;算例2中块石覆盖区域的迎浪侧最大液化深度0.8 m,背浪侧最大液化深度0.7 m。在算例2中块石覆盖区域依旧存在液化现象,但液化深度小于算例1中未铺设块石时,而算例3中块石覆盖区域不发生液化,抗液化效果最为显著。分析可知,块石层堆积越厚,抗液化效果越显著。
5 结语
本文通过采用基于开源软件OpenFOAM建立的CFD-CSD耦合模型,来研究波浪作用下的海上风电复合筒型基础周围海床的抗液化效果。通过数值模拟海床表面上覆块石对抗液化的效果,得出上覆块石的厚度是抗液化的重要参数。当块石厚度越大,抗液化的效果越好。铺设块石防液化的原理在于减小海床动有效应力,而与海床超静孔隙水压力无关。而其它的上覆块石抗液化影响因素还需要进一步的研究探索。
[1]MADABHUSHI S P G.Ground improvement methods for liquefac原tion remediation[J].Proceedings of the Institution of Civil Engi原neers-Ground Improvement,2007,11(4):195-206.
[2] SUMER B M,DIXEN F H,FREDS椎E J.Cover stones on liquefi原able soil bed under waves[J].Coastal Engineering,2010,57(9):864-873.
[3] SUMER B M,DIXEN F H,FREDS椎E J.Stability of submerged rock berms exposed to motion of liquefied soil in waves[J].Ocean Engineering,2011,38(7):849-859.
[4] L佼PEZ-QUEROL S,BL佗ZQUEZ R.Identification of failure mech原anisms of road embankments due to liquefaction:optimal corrective measures at seismic sites[J].Canadian Geotechnical Journal,2006,43(9):889-902.
[5] 肖金龙,张金凤,张庆河,等.波浪作用下海上风力发电装置基础海床的液化研究[J].港工技术,2013(4):46-49.XIAO Jin-long,ZHANG Jin-feng,ZHANG Qing-he,et al.Study on liquefaction of seabed around offshore wind power facilities foundation under wave[J].Port Engineering Technology,2013(4):46-49.
[6] 于聪,张金凤,张庆河援复合筒型基础周围土体在波浪作用下的动力响应[J].中国港湾建设,2015,35(1):1-5援YU Cong,ZHANG Jin-feng,ZHANG Qing-he.Wave-induced seabed dynamic response around composite bucket foundation[J].China Harbour Engineering,2015,35(1):1-5.
[7] 陈宝清,张金凤,史小康.基于OpenFOAM的波浪作用下海床动力响应[J].中国港湾建设,2017,37(3):1-5.CHEN Bao-qing,ZHANG Jin-feng,SHI Xiao-kang.Numerical simulation for the dynamic response of seabed under waves based on the OpenFOAM[J].China Harbour Engineering,2017,37(3):1-5.
[8] YE J.3D liquefaction criteria for seabed considering the cohesion and friction of soil[J].Applied Ocean Research,2012,37(4):111-119.
[9] 韩涛,张庆河,张金凤,等.波浪作用下砂质海床最大液化深度[J].中国港湾建设,2006,26(2):27-28.HAN Tao,ZHANG Qing-he,ZHANG Jin-feng,et al.Maximum liquefaction depth of sandy seabed under waves[J].China Harbour Engineering,2006,26(2):27-28.
