冻土热物理性质的统计特征及分布规律

石梁宏，李双洋，王冲，尹楠



冻土热物理性质的统计特征及分布规律

石梁宏1, 2，李双洋1，王冲3，尹楠1

(1. 中国科学院 西北生态环境资源研究院 冻土工程国家重点实验室，甘肃 兰州，730000； 2. 中国科学院大学，北京，100049；3. 兰州大学 土木工程与力学学院，甘肃 兰州，730000)

为揭示冻土热物理性质的随机性及内在规律，以青藏高原粉质黏土为研究对象，分别对5种典型温度条件下冻土的热物理参数进行50组大样本测试。研究结果表明：即使在同一温度下，试样的热物理参数也存在明显的随机性，但又呈现出一定的统计规律；冻土的热物理参数(导热系数和容积热容量)服从正态分布或对数正态分布，并利用总体分布假设的2检验法验证了分布规律的正确性。

冻土；热物理性质；导热系数；容积热容量；概率分布；2检验法

近年来，随着国民经济的发展，我国对高寒、高海拔地区的开发力度不断加大，一系列的重大工程逐渐在冻土地区修建，如何保证这些工程的稳定性一直是施工建设中所关注的热点问题[1]。作为一种多相介质材料，冻土主要由固体土颗粒、未冻水、冰晶体和空气等组成[2]，其物理力学性质对外界环境的变化十分敏感。由于含水量、干密度等内部因素和气候变化、工程扰动等外部因素的相互作用，不可避免地会改变土体的热物理性质，进而影响到土水体系与外界环境之间的热交换过程，由此可能引发次生的不良冻土现象，直接影响到工程的稳定性[3−5]。因此，为了保证冻土地区工程设计和施工的安全，满足结构稳定性的要求，对冻土的热物理性质进行研究具有十分重要的意义。目前，对土体热物理性质的研究主要集中在对热参数的试验测试和影响因素分析2个方面。在热参数的测试方面，国内的相关规范以表格的形式给出了几种典型土在不同密度和不同含水量下的热物理参 数[6−8]。此外，叶万军等[9]对不同含水率下黄土的导热系数进行了测试；OVERDUIN等[10]对相变区附近的土体导热系数进行了研究；徐捷等[11]对淤泥质黏土在高温下的导热系数进行了研究；谈云志等[12]提出了非饱和土热导率的预估模型。在热参数的影响因素分析方面，马祖罗夫[13]通过对大量文献的研究，给出了冻融土的热物理性质与其颗粒组成、容重、含水率、饱和度、孔隙率、密度、塑限之间的关系；陶兆祥等[14]研究了容重和含水量的变化对高含水(冰)冻融土导热系数的影响；ABU-HAMDEH[15]研究了干密度对砂土热导率的影响；ORAKOGLU等[16]考虑了冻融循环次数、纤维体积含量对加筋土体导热系数的影响；COSENZA等[17]研究了初始体积含水量对土体导热系数的影响。以上工作都是将土体的热物理参数视为一个确定值来展开研究，但是在实际的工程中，尤其在负温条件下，由于土体的含水量、含冰量、密度等因素分布的不均匀性，即使在同一温度下，土体的热物理参数也呈现出很强的离散性和随机性。当前的工程热工计算是用乘以安全系数的方法考虑热参数的离散性，这种计算势必会增加工程成本，无法保证工程的经济性，如果不考虑热参数的随机特征，又可能会影响到工程的安全性。因此，为了描述土体热物理参数的随机分布特点，采用概率论与数理统计的方法研究冻土热参数的统计特征及分布规律，为深入分析冻土类材料的热物理性质提供理论依据和参考。目前，对冻土热物理参数不确定性及离散现象的研究较少，吴晓光[18]对高温冻土的热参数进行了统计分析，给出了高温冻土热参数的概率分布函数，但是缺少对其分布函数进行假设检验，且该研究仅限于−1.5 ℃的高温冻土，因而其成果应用有一定的局限性。本文作者对青藏高原粉质黏土在不同温度条件(20，−1，−2，−5和−10 ℃)下的热物理参数(导热系数、容积热容量)分别进行50组大样本试验，通过对试验数据离散程度及分布规律的统计分析，得到冻土热物理参数的概率分布函数，并从理论上验证提出的分布规律的正确性，为进一步研究冻土类材料及工程的热力学性质提供 依据。

1 分布规律模型及检验方法

概率分布函数是研究随机变量的重要工具，为了描述冻土热物理性质的随机分布特点和统计特征，引入3种典型的概率分布函数(正态分布、对数正态分布、威布尔分布)；同时，为了验证概率分布函数的正确性，采用χ2检验法对分布函数进行假设检验。

1.1 分布规律模型

1.1.1 正态分布

正态分布的概率密度函数()：

式中：为样本值；为正态分布的期望；为正态分布的标准差(＞0)。

正态分布的累积分布函数为

1.1.2 对数正态分布

对数正态分布的概率密度函数()：

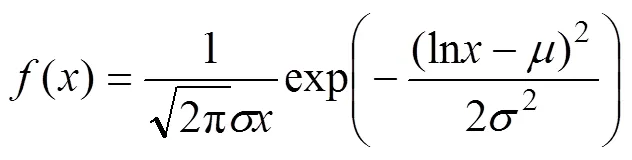
式中：为样本值；为对数正态分布的均值；为对数正态分布的标准差。

对数正态分布的累积分布函数为

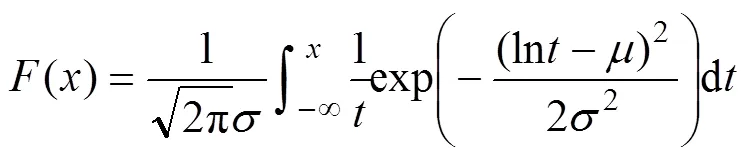
1.1.3 威布尔分布

威布尔分布的概率密度函数()：

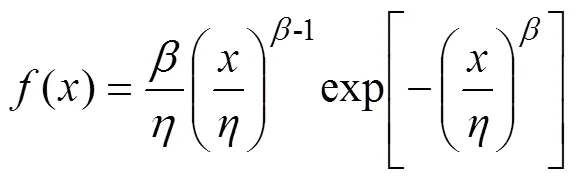
式中：为样本值；为威布尔分布的形状参数；为威布尔分布的尺度参数。

威布尔分布的累积分布函数为

利用最大似然估计法可求得正态分布、对数正态分布、威布尔分布中的未知参数，进而可得到对应的概率分布函数。

1.2 χ2检验法

当不确定随机变量的总体服从何种类型分布时，利用2检验法可检验关于总体分布的假设。首先，根据样本数据的分布特征，提出样本总体可能服从某一概率分布的假设，记为0。由样本观测值求得

式中：2为统计量，可通过样本值求出；f为试验频率；p为估计频率；为样本容量。

若在假设0下，由式 (7)计算后有

则在显著性水平下假设检验通过[19]。式(8)中：为显著性水平；为划分的样本子集个数；为计算概率分布时未知参数的个数。

2 试验

2.1 试验土样

试验土样为青藏铁路北麓河试验段粉质黏土。将原状土过孔径2 mm筛后，取粒径小于2 mm的土样作为本次试验用土。试样的基本物理参数见表1。

表1 试样的基本物理参数

2.2 试验仪器

试验主要使用QL–30热分析仪测定试样的热物理参数，该热分析仪的工作原理为非稳态法中的热脉冲法。

通过可控式恒温冰箱调节不同的测试温度(20，−1，−2，−5和−10 ℃)，冰箱中设置了温度探头，调节冰箱温度可模拟5种温度条件。

2.3 试验步骤

试验所用土样的干密度为1.82 g/cm³，含水量为10.00%。试验步骤如下。

1) 称取一定量的土样烘干，根据所需含水量，将去离子水均匀喷洒在土样上，经过充分搅拌后装入盛土容器中密封24 h，以保证水分在土样中扩散均匀。

2) 将土装入制样的标准模具中，制备直径×高度为61.80 mm×50.00 mm的试样50个。在制备试样的过程中，严格要求分层装入土样，从而保证试样截面的平整性，试样制备完成后，立即用保鲜薄包裹，以减少水分蒸发。

3) 根据GB/T 50123—1999“土工试验方法标 准”[20]，将试样置于恒温冰箱，设置试验温度(温度分别为20，−1，−2，−5和−10 ℃)后等待48 h，使得整个试样温度达到测试温度。

4) 连续3次测定试样表面温度，当3次的温差小于0.1 ℃时，则认为温度稳定，可进行冻土热参数的测量试验。

3 试验结果及统计特征分析

3.1 试验结果

将制备的50个试样放入冰箱，测试每种温度下各组试样的导热系数和容积热容量。不同温度条件下各组试样导热系数和容积热容量的测定值如图1和图2所示。

图1 各组试样的试验导热系数测定值

3.2 统计特征分析

图3和图4所示分别为导热系数和容积热容量试验数据的箱形图，箱形图可直观地反映出数据的离散特点。从图3可以看出：在同一温度下，试样导热系数的离散性均较大；当温度为20 ℃时，导热系数的变化范围为1.281~1.471 W·m−1·K−1，最大值和最小值之间相差15.0%；在−1 ℃时，导热系数最大相差 0.197 W·m−1·K−1，最大值和最小值之间相差14.8%；在−2 ℃时，导热系数最大相差0.079 W·m−1·K−1，最大值和最小值之间相差5.4%，为5种试验温度下的最小差值；在−5 ℃时，导热系数最大值和最小值之间相差7.5%；在−10 ℃时，导热系数最大相差6.2%。

图2 各组试样的试验容积热容量测定值

图3 各组试样导热系数的箱形图

图4 各组试样容积热容量的箱形图

由图4可以看出：在同一温度下，试样的容积热容量不是某一确定值，也呈现出较强的离散性。例如，在20 ℃时，容积热容量的变化范围为1.45~1.50 MJ·m−3·K−1，其他4种温度下的容积热容量也均在一定的范围内波动。

经过对试验数据分析后发现：在同一温度下，冻土的热物理参数(导热系数、容积热容量)存在较强的离散性和随机性，用确定的数值来描述冻土的热物理参数并不符合实际，因而需要对其进行概率统计分析。

4 热物理性质的分布规律分析

将每个温度下冻土热物理参数(导热系数和容积热容量)的试验值代入正态分布、对数正态分布和威布尔分布中，绘制出3种典型分布函数的理论概率分布图像；然后，根据理论概率分布和实测概率分布图像的吻合情况，提出热物理参数可能服从的概率分布假设；最后，利用2检验法进行假设检验，验证所提出分布函数的正确性。

4.1 导热系数的分布概型确定

将每个温度下导热系数的50个数据分别代入式(2)，(4)，(6)，得到3种理论概率函数的分布图像，然后与实测概率分布图像进行比较。图5所示为根据导热系数的分布情况后假设的3种函数概率分布及实测概率分布图像。从图5可以看出：正态或对数正态的概率分布与实测值的概率分布吻合得更好。

表2所示为计算理论与实测概率分布曲线的最大差值，其中，威布尔分布的差值较大，尤其在20 ℃和−5 ℃下，威布尔的概率分布与实测概率分布的差值分别为0.322 6和0.463 6；而正态和对数正态的概率分布均与实测概率分布相差较小，其中最大差值出现在−10 ℃下，相差仅为0.109 9。为了验证导热系数是否满足假设的3种经典分布，本文利用2检验法对导热系数可能服从的概率分布函数进行假设检验。

根据2检验法，检验各温度条件下假设的导热系数的分布函数。首先由概率分布曲线的吻合情况，提出导热系数可能服从的概率分布假设0，通过式(7)和(8)计算2可判断假设的函数是否成立。假设的导热系数概率分布函数2的计算结果如表3所示。从表3可以看出：在20 ℃和−5 ℃下，威布尔分布的2均较高，超出了其限值2α(−−1)，故拒绝在20 ℃和−5 ℃下导热系数服从威布尔分布的假设。而在5种温度条件下，正态分布和对数正态分布的2均在其限值范围内，即在不同温度下，均可接受导热系数服从正态分布或对数正态分布的假设。

温度/℃：(a) 20；(b) −1；(c) −2；(d) −5；(e) −10

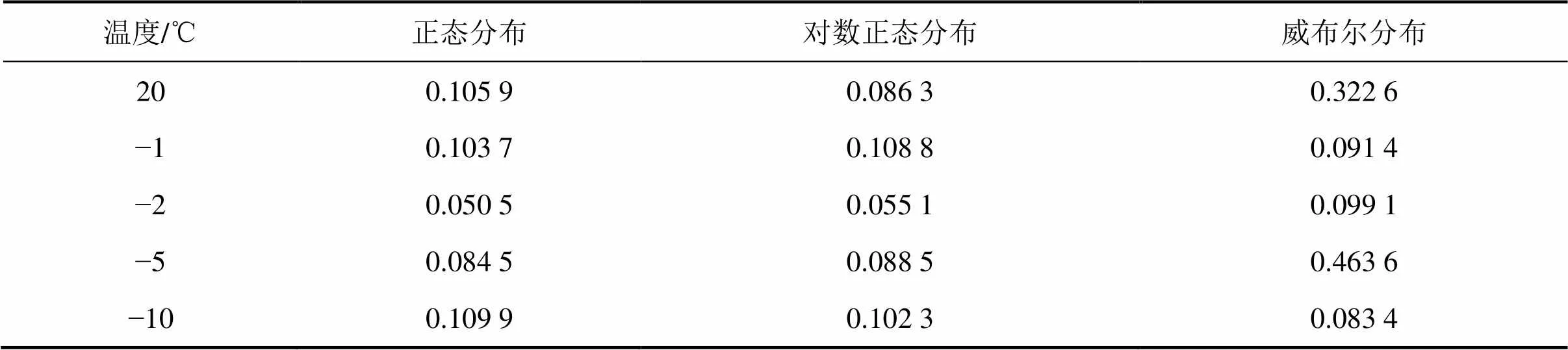
表2 导热系数实测概率分布与理论概率分布之间的最大差值

结合表2、图5以及表3可以得到：在5种温度下，正态或对数正态的概率分布与实测导热系数的概率分布更接近，且能通过假设检验。因此，总体来看，不同温度下导热系数的概率分布适宜采用正态分布或对数正态分布描述。

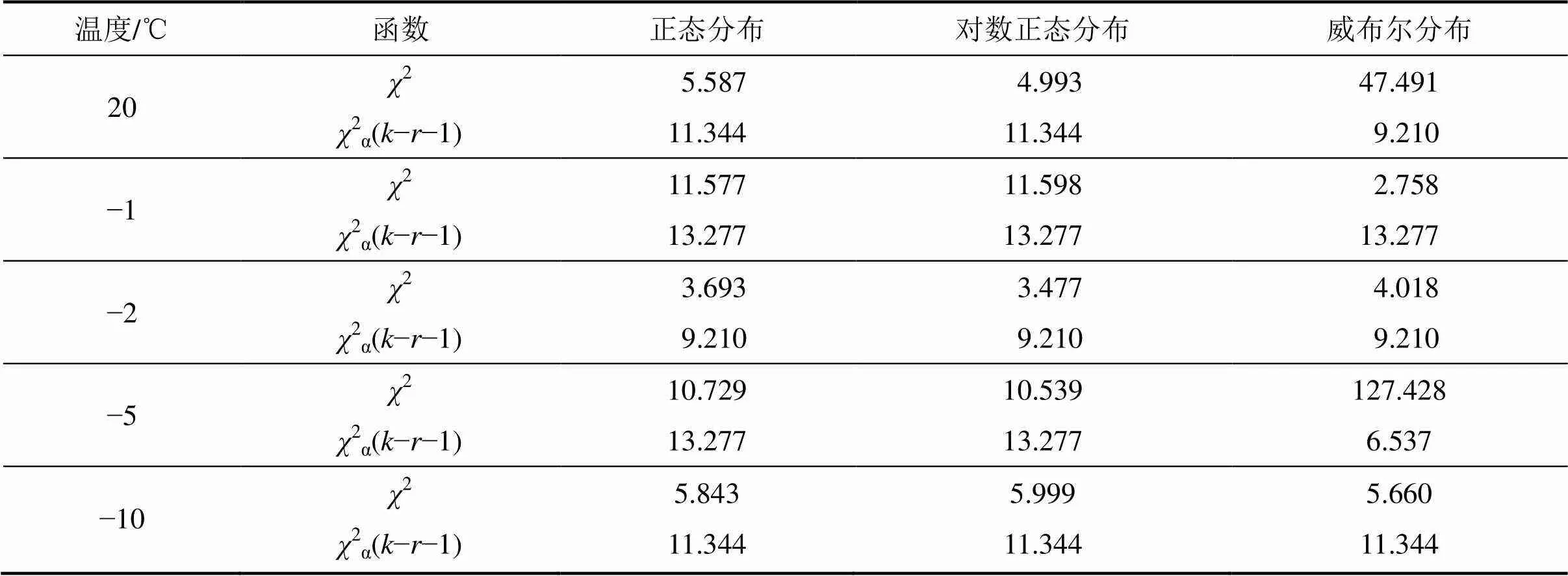
表3 不同温度下各个分布的χ2(α=0.01)

4.2 容积热容量分布概型的确定

将每个温度下容积热容量的试验值代入式(2)，(4)和(6)，得到3种理论概率函数的分布图像，然后与实测概率分布图像进行比较(见图6)。

从图6可以看出：假设的3种容积热容量的理论概率分布曲线与实测概率分布曲线都较接近；在20，−1，−2和−10 ℃下，正态和对数正态的概率分布与实测概率分布的吻合程度更高；而在−5 ℃下，威布尔的概率分布与实测值的概率分布吻合得更好。

表4所示为统计假设的3种容积热容量概率函数分布与实测概率分布的最大差值。从表4可以得出，在不同的试验温度下，正态和对数正态的概率分布与实测概率分布的差值均较小，其中，最大差值出现在−2 ℃时的正态分布下，相差仅为0.109 3；相比之下，威布尔的概率分布与实测概率分布之间的差值均较大。同样，采用2检验法，对不同温度下容积热容量可能服从的概率分布函数进行假设检验。根据式(7)和(8)计算2后，可判断假设是否成立。

温度/℃：(a) 20；(b) −1；(c) −2；(d) −5；(e) −10

表4 容积热容量实测概率分布与理论概率分布之间的最大差值

不同温度下各种分布概型的2如表5所示。由表5可以看出：在20、−1、−2、−5和−10 ℃下，3种理论分布的2均小于2(−−1)。故综合来看，假设检验通过，3种理论分布函数均可描述不同温度下冻土容积热容量的分布规律。

结合图6和表5可以得出：正态和对数正态的概率分布与实测容积热容量的概率分布差值更小，吻合效果更好，且能通过假设检验。故总体来看，不同温度下容积热容量的概率分布更适宜采用正态分布或对数正态分布进行描述。

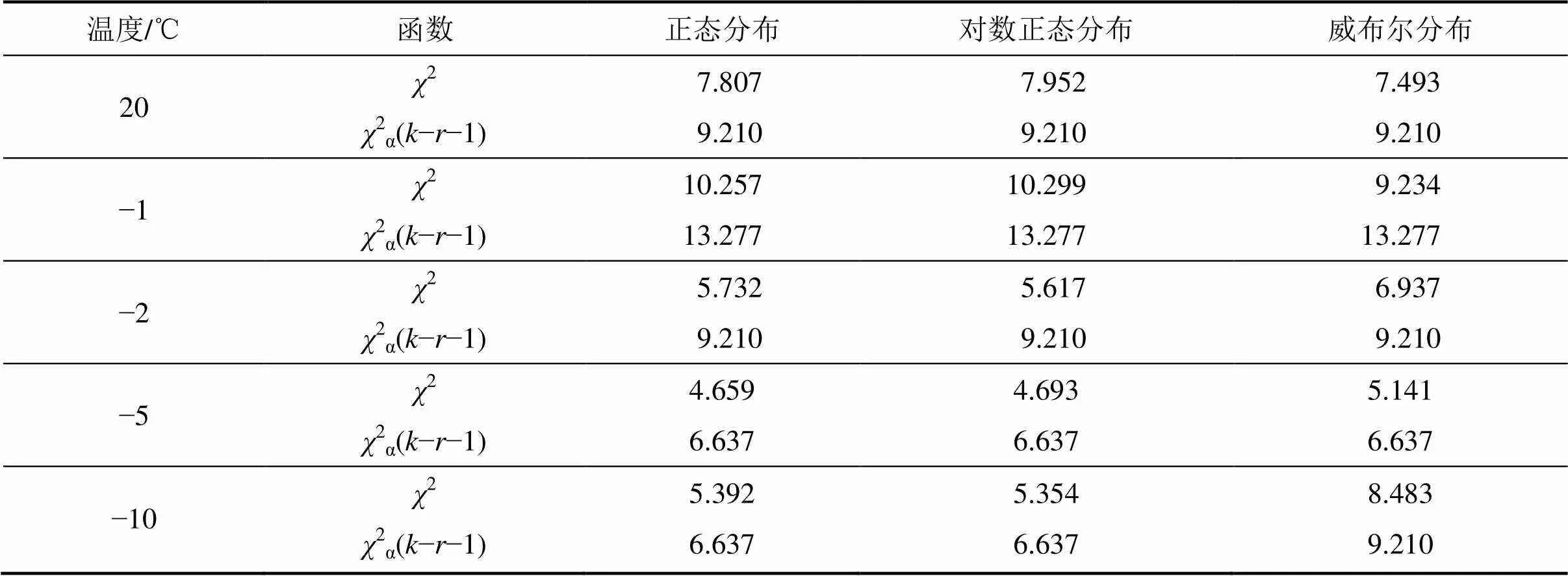
表5 不同温度下各种分布概型的χ2(α=0.01)

5 结论

1) 由于密度、水分和含冰量等内部因素的不均匀性，以及工程扰动、气候变化等外界因素的影响，冻土的热参数呈现出较强的离散性，但又具有一定的统计规律，因此，使用某一确定值来描述冻土的热参数并不合理，而采用概率分布函数对热参数的分布规律进行描述更准确。

2) 在进行冻土导热系数和容积热容量的统计特征分析时，均宜采用正态分布或对数正态分布。

3) 本文通过对冻土热参数的随机性和统计特征进行分析研究，得到了描述冻土热物理性质分布规律的概率函数，并采用2检验法对所提出分布函数的正确性加以验证。本文所提出的冻土热物理性质的分布规律可为今后冻土材料的研究和工程热力学的计算提供参考。

[1] 徐斅祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001: 250−281. XU Xiaozu, WANG Jiacheng, ZHANG Lixin. Frozen soil physics[M]. Beijing: Science Press, 2001: 250−281.

[2] 马巍, 王大雁. 冻土力学[M]. 北京: 科学出版社, 2014: 1−37. MA Wei, WANG Dayan. Mechanics of frozen ground[M]. Beijing: Science Press, 2014: 1−37.

[3] 马巍, 穆彦虎, 李国玉, 等. 多年冻土区铁路路基热状况对工程扰动及气候变化的响应[J]. 中国科学: 地球科学, 2013, 43(3): 478−489. MA Wei, MU Yanhu, LI Guoyu, et al. Responses of embankment thermal regime to engineering activities and climate along the Qinghai-Tibei Railway[J]. Scientia Sinica Terrae, 2013, 43(3): 478−489.

[4] LI Shuangyang, LAI Yuanming, ZHANG Mingyi, et al. Seasonal differences in seismic responses of embankment on a sloping ground in permafrost region[J]. Soil Dynamics and Earthquake Engineering, 2015, 76: 122−135.

[5] 程国栋, 马巍. 青藏铁路建设中冻土工程问题[J]. 自然杂志, 2015, 28(6): 315−320. CHENG Guodong, MA Wei. Frozen soil engineering problems in construction of the Qinghai-Tibet Railway[J]. Chinese Journal of Nature, 2015, 28(6): 315−320.

[6] GB/T 50324—2014, 冻土工程地质勘察规范[S]. GB/T 50324—2014, Code for engineering geological investigation of frozen ground[S].

[7] 原喜忠, 李宁, 赵秀云, 等. 非饱和(冻)土导热系数预估模型研究[J]. 岩土力学, 2010, 31(9): 2690−2694. YUAN Xizhong, LI Ning, ZHAO Xiuyun, et al. Study of thermal conductivity model for unsaturated unfrozen and frozen soil[J]. Rock and Soil Mechanics, 2010, 31(9): 2690−2694.

[8] JGJ 118—2011, 冻土地区建筑地基基础规范[S]. JGJ 118—2011, Code for design of soil and foundation of building in frozen soil region[S].

[9] 叶万军, 董西好, 杨更社, 等. 含水率和干密度对黄土热参数影响的试验研究[J]. 岩土力学, 2017, 38(3): 656−662. YE Wanjun, DONG Xihao, YANG Gengshe, et al. Effect of moisture content and dry density on thermal parameters of loess[J]. Rock and Soil Mechanics, 2017, 38(3): 656−662.

[10] OVERDUIN P P, KANE D L, VAN LOON W K P. Measuring thermal conductivity in freezing and thawing soil using the soil temperature response to heating[J]. Cold Regions Science and Technology, 2006, 45(1): 8−22.

[11] 徐捷, 朱合华, 闫治国. 淤泥质黏土火灾高温下导热系数的试验研究[J]. 岩土工程学报, 2012, 34(11): 2108−2113. XU Jie, ZHU Hehua, YAN Zhiguo. Experimental studies on coefficient of thermal conductivity of silty clay[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2108−2113.

[12] 谈云志, 喻波, 胡新江, 等. 非饱和土热导率预估模型研究[J]. 岩土工程学报, 2013, 35(1): 129−133. TAN Yunzhi, YU Bo, HU Xinjiang, et al. Prediction model for thermal conductivity of unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 129−133.

[13] 马祖罗夫Г П. 冻土物理力学性质[M]. 梁惠生, 伍期建, 译. 北京: 煤炭工业出版社, 1980: 15−40.МАЗУРОВ Г П. Physical-Mechanical property of frozen soil[M]. LIANG Huisheng, WU Qijian, Trans. Beijing: China Coal Industry Publishing House, 1980: 15−40.

[14] 陶兆祥, 张景森. 大含水(冰)量融冻土导热系数的测定研究[J]. 冰川冻土, 1983, 5(2): 75−80. TAO Zhaoxiang, ZHANG Jingsen. The thermal conductivity of thawed and frozen soils with high water(ice) content[J]. Journal of Glaciology and Geocryology, 1983, 5(2): 75−80.

[15] ABU-HAMDEH N H. Measurment of the thermal conductivity of sandy loam and clay loam soils using single and dual probe[J]. Journal of Agricultural Engineering Resrarch, 2001, 80(2): 209−216.

[16] ORAKOGLU M E, LIU Jiankun, NIU Fujun. Experimental and modeling investigation of the thermal conductivity of fiber-reinforced soil subjected to freeze-thaw cycles[J]. Applied Thermal Engineering, 2016, 108: 824−832.

[17] COSENZA P, GUÉRIN R, TABBAGH A. Relationship between thermal conductivity and water content of soils using numerical modelling[J]. European Journal of soil Science, 2003, 54(3): 581−587.

[18] 吴晓光. 概率统计在高温冻土热学及力学性质研究中的应用[D]. 兰州：兰州大学土木工程与力学学院, 2013: 10−23. WU Xiaoguang. The application of probability and statistics in the study on thermal and mechanical properties of warm frozen soil[D]. Lan Zhou: Lanzhou University. College of Civil Engineering and Mechanics, 2013: 10−23.

[19] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008: 1−20. SHENG Zhou, XIE Shiqian, PAN Chenyi. Probability and mathematical statistics[M]. 4th ed. Beijing: High Education Press, 2008: 1−20.

[20] GB/T 50123—1999, 土工试验方法标准[S]. GB/T 50123—1999, Standard for soil test method[S].

Statistical characters and distribution laws of thermophysical properties of frozen soil

SHI Lianghong1, 2, LI Shuangyang1, WANG Chong3, YIN Nan1

(1. State Key Laboratory of Frozen Soil Engineering, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. College of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China)

To reveal the randomness and intrinsic regularity of the frozen soil, thermal physical parameters of 50 sets of silty clay in Qinghai—Tibet Plateau were tested in each temperature state. The result shows that even though under the same temperature, the thermal parameters of samples exhibit great randomness and uncertainty, but obey statistical rules to some extent. According to the analysis with probability and mathematical statistics method, the thermal physical parameters (thermal conductivity and volumetric heat capacity) of the frozen soil obey normal distribution or lognormal distribution, and this hypothesis is proven to be valid by the2hypothesis testing method.

frozen soil; thermophysical property; thermal conductivity; volumetric heat capacity; probability distribution;2testing method

10.11817/j.issn.1672−7207.2018.12.020

TU411.2

A

1672−7207(2018)12−3060−08

2018−01−29；

2018−03−18

国家自然科学基金资助项目(41672315, 41230630)；中国科学院前沿科学重点研究项目(QYZDY-SSW-DQC015)；中国科学院“西部之光”项目(2014)；中国科学院青年创新促进会项目(2015349)；冻土工程国家重点实验室自主研究课题(SKLFSE-ZY-18)；中国科学院STS项目(HHS-TSS-STS-1502)(Projects(41672315, 41230630) supported by the National Natural Science Foundation of China; Project(QYZDY-SSW-DQC015) supported by Key Research Program of Frontier Sciences of Chinese Academy of Sciences; Project(2014) supported by Light of West China Program of Chinese Academy of Sciences; Project(2015349) supported by Youth Innovation Promotion Association of Chinese Academy of Sciences; Project(SKLFSE-ZY-18)supported by State Key Laboratory of Frozen Soil Engineering; Project (HHS-TSS-STS-1502) supported by STS Project of Chinese Academy of Sciences)

李双洋，博士，副研究员, 从事冻土力学与寒区岩土工程研究; E-mail：lisy@lzb.ac.cn

(编辑 赵俊)