基于图像分割的目标尺寸特征测量

王 颖，王鹏飞，杨余旺

(南京理工大学 计算机科学与工程学院，江苏 南京 210094)

1 概 述

不同于传统的测量方式需要与物体直接接触，图像测量技术不需要直接接触被观测物体，这样不会对被观测物体造成影响，观测者也处于安全地带。运用图像分析技术能够对传统方法不易测量的物理量进行测量，例如过于微小或者物体上的个别部分等[1]。除此之外，如对象处于人不能到达或者不能长时间停留的恶劣环境，也可以通过先投放或预设的采集设备采集图像后再进行处理分析。更优越的是，图像测量的自动化程度高，图像的采集、处理、分析、理解可由计算机程序预先设定，无需人工干涉，减少了工作量和时间。相比于直接测量，图像测量需要对硬件图像采集系统的参数进行标定和修正，这直接影响了测量的精度和正确性。对图像采集系统的标定和误差修正需要使用数字图像处理技术，这是后续对象测量的先觉条件和基础[2]。

随着计算机技术和硬件设备的高速发展，国内外的图像测量应用和技术都有了很大进展，众多领域都需要进行尺寸测量，应用范围涵盖到工业元件的尺寸测量、物体形状子检测、模式匹配等诸多方面[3]。

文中研究了基于边缘检测的霍夫变换对矩形等规则形状的检测和最小外接矩形对不规则形状的检测。其关键思想是：检测出目标的矩形度，根据矩形度的大小选择霍夫变换或最小外接矩形法检测目标矩形，然后计算目标的尺寸特征。

2 图像分割

文中算法属于图像分割技术，图像分割是一种计算机视觉技术，是进行图像分析的基础。它用于将图像划分出需要关注的目标或区域相关的部分，可以分为完全分割和局部分割[4]。文中主要使用两种分割技术：基于边缘分割和基于区域分割[5]，这两种方法解决了一个对偶问题。每个区域可以用该区域的封闭边界表示，而任意封闭边界也可以显示一个区域。

图像采集时同时采集多个目标，经OSTU(大津法或最大类间方差法)分割后，再用标记法标记多个目标，分别分割出来后，对每个目标逐个进行运算测量。

基于边缘的分割对应上文中的局部分割，先使用边缘检测子检测出图像的边缘，再在边缘图像上进行处理，边缘图像中的强度最高的就是图像在灰度、颜色、纹理等维度上梯度较大的位置。但边缘检测子直接检测到边缘图像后必须采用后续步骤将边缘合并为边缘链，这样才能形成闭合边界，从而更好地拟合图像真实边界。最终目的是至少完成部分分割，将局部边缘集成到一幅图像中，使图像中只存在与目标物体对应的边缘链。基于边缘的分割会出现两个常见的错误：一是在没有真实边界的位置生成噪声边缘；二是在实际存在边界的位置没有产生边缘点，这是受图像噪声或图像中的不当信息影响造成的。这样的错误对分割结果有显著的负面影响。

在分割处理之前掌握越多的先验知识，获得的分割效果越好。例如，文中可以先计算目标的矩形度：

(1)

其中，As为连通域S的面积；Ar为包围该连通域的最小矩形面积。根据一定训练集的训练，得到最优的阈值Prt，若测得Pr>Prt，则选用霍夫变换方法，否则选用最小外接矩形方法。

3 特征提取检测算法

由于物体的走向随机，图像中水平和垂直方向的度量不一定是所需要的，所以有必要确定物体的主轴并测量与之相关的长度和宽度。主轴可用内部点拟合直线或者应用物体的最小外接矩形。根据目标特征选择不同检测方法，若是矩形度高，选择霍夫变换；若矩形度低于阈值，选择最小外接矩形。

3.1 霍夫变换法

霍夫变换[6]是一种检测图像中线性结构的有效方法。文中使用的是基于梯度信息改进的霍夫变换，流程为图像采集、预处理、边缘检测。重点是利用梯度信息，缩小霍夫变换搜索范围，提高效率和准确度。

边缘检测提取出对象的边界点集[7]，由于噪声的存在，得到的边缘通常是孤立的或分小段连续的。所以需要某种算法将边缘的点连接或找出某种规律，然后进行后续处理。霍夫变换[8]利用像素空间和参数空间两个空间之间的变换，在同一个像素空间有相同形状参数的曲线或直线变换到参数坐标空间会在一个点上形成峰值，从而把像素空间检测形状参数的问题转化为参数空间统计峰值问题。

在直角坐标系下，一条直线可以表示为：

y=kx+b

(2)

霍夫变换的原理就是点线对偶性[9]，两个空间的参数和变量可以相互转换，即像素空间上一定点坐标x,y作为参数，k,b作为坐标轴变量，这样k,b就对应参数空间自变量和因变量。一个空间的点对应另一个空间的线，线对应另一个空间的点。所以要检测边界点集共有的线参数，只需要找到参数空间线的相交点即可。

k,b的值都可能趋近无穷大，如当直线倾角接近90°，k的值会逼近无穷大。为了计算方便，将参数空间使用极坐标表示，直线的极坐标方程如下：

xcosθ+ysinθ=ρ

(3)

其中，ρ表示坐标原点到直线的距离；θ表示直线与横坐标的夹角。

由于同一条直线上的点具有一致参数(γ,θ)，因此可以先检测出图片的边缘，然后对图像上每一个边缘像素点，在参数极坐标下变换为一条正弦曲线，像素空间中在同一条直线上的点映射到参数空间就是多条正弦曲线，它们会相交于一点[10]，该点具有相同的直线参数。霍夫变换就是用该基本思想进行直线检测。

图像空间点对应参数极坐标系的正弦曲线如图1所示。

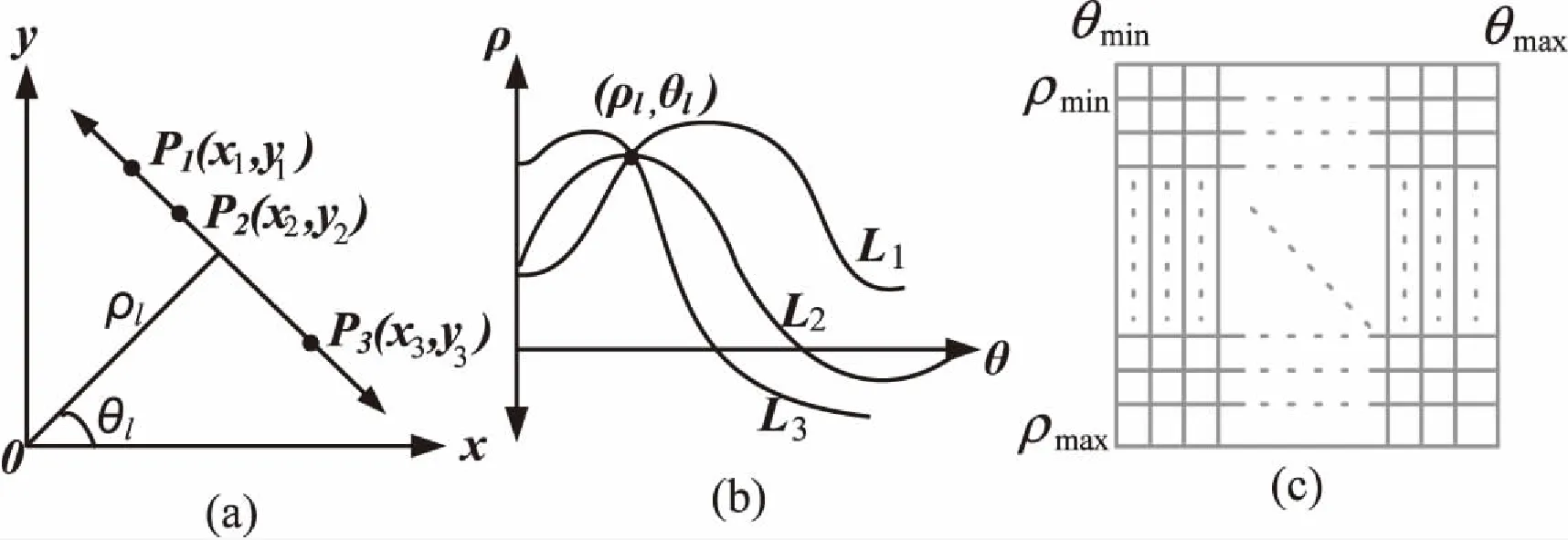
图1图像空间点对应参数极坐标系的正弦曲线

为检测规则的四边形，可根据四边形的特殊几何特征。矩形的几何特征包括：具有四条直线，两两成对，针对任意一条直线，有一条直线与之平行，还有两条与之垂直。根据边缘直线的检测结果，可以判断图像中是否存在矩形图形[11]，有几个，并且计算矩形几何参数。

矩形检测算法如下：

算法1：矩形检测算法。

输入：包含目标的二值图像；

输出：矩形尺寸参数。

(1)边缘检测；

(2)应用霍夫变换算法求出4个峰值点，对应原图像中边缘的4条直线，即矩形的4条边所在直线；

(3)由4条直线的参数，根据几何学可以求出4个交点的坐标，交点成对求距离可获得矩形尺寸参数；

(4)将4个交点坐标连线，获得矩形的轮廓线。

这一类方法还可以用来检测多种由直线段组成的几何图形，如梯形、三角形等。文中的改进在于利用了梯度信息，由于霍夫变换选择峰值点时，会受到拐角的影响导致较大误差，同时可能选取到同一方向部分边界的两段略有差异的线段造成检测测量失败。利用边缘检测时得到的梯度方向，由于是规则形状如平行四边形，梯度方向应该有两个，根据这两个方向分割边缘点集，而后分别做霍夫变换。

3.2 最小外接矩形法

本节致力于找到一个能覆盖输入的两维面积最小的任意偏向矩形-最小包围矩形(MER)[12]，然后根据找到的矩形，提取矩形的长度和宽度，即为目标的长轴长度和短轴长度。

初始状态为长轴与坐标系x轴-90°的矩形，长在水平方向，宽在竖直方向。在[-90°,0°)区间以每次顺时针旋转一个增量，最后选取面积最小的矩形。最小面积就是目标连通区域的边界矩形，可根据角度和截距计算外接矩形的面积(见图2)，公式如下：

area=(h1-h2)·(h3-h4)·|cosα·sinα|

(4)

图2 最小外接矩形几何计算

凸包旋转法是根据任意多边形的外接矩形的每一条边与其凸多边形至少有一个交点的原则设计的，具有比单纯旋转法更好的速度和精确性。计算多边形的最小凸包，在所得凸包中选择一条边作为起始边，并绕该边左顶点旋转，直至该边平行于x轴。最后计算并保存其最小外接矩形(MBR)的坐标、边的编号及旋转角度。依次选择剩下的边，并按照同样方法计算并保存同样的度量。比较所得的MBR的面积，找到面积最小的对应的旋转角度和边，以该边的左端点为圆心逆向旋转就是所求的MABR。

显而易见，任意一个多边形的MABR必定经过它的凸包的一条边，由此可以推导出以上算法所求得的MABR为准确解。

3.3 自适应研究

算法的自适应研究(Self-Aadaptation)是指根据物体、控件的不同恰当地挑选自身的算法，或调节算法的参数以适应物体、控件的多样性，用户的不同需求和系统自身容错的需求。通过检测目标的形状，对目标的形状进行描述，提取特定的特征来表示。例如以下几个简单的几何特征，如凹凸面积、矩形度、紧密度等。

矩形度已经在上文阐述了。紧密度是用来表示目标区域的形状是否紧密的度量：

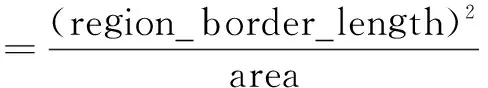
(5)

根据这几个特征自适应地选择以上两种方法。

4 算法设计实现

4.1 霍夫检测矩形

通过检测两个正交方向上的直线，从而检测矩形。算法如下：

算法2：霍夫变换四边形检测。

输入：包含多个目标的图像；

输出：多个目标的多个矩形参数。

(1)图像预处理；

(2)OTSU算法二值化，删除小面积连通区域；

(3)区域标记；

(4)选择一个目标区域，进行边缘检测；

(5)对边缘使用改进的霍夫变换检测出四条边；

(6)重复步骤(4)和(5)，直到所有区域都被选择过。

4.2 最小外接矩形检测

使用的最小外接矩形算法如下：

算法3：最小外接矩形检测。

输入：包含多个目标的图像；

输出：多个目标的多个外接矩形参数。

(1)图像预处理；

(2)OTSU算法二值化，删除小面积连通区域；

(3)区域标记；

(4)选择一个目标区域，进行最小外接矩形检测；

(5)重复步骤4，直到所有区域都被选择过。

5 实验结果与分析

使用工业相机拍摄的多个元件的图像作为实验数据。实验图像需要经过校正以及配准等预处理工作[13]，选取各个区域进行分割、处理、测量分析。文中选取出一个区域进行展示，已经进行圈划标注。实验装置和拍摄图片如图3所示。

图3 装置和实验图

实验系统截图如图4所示。

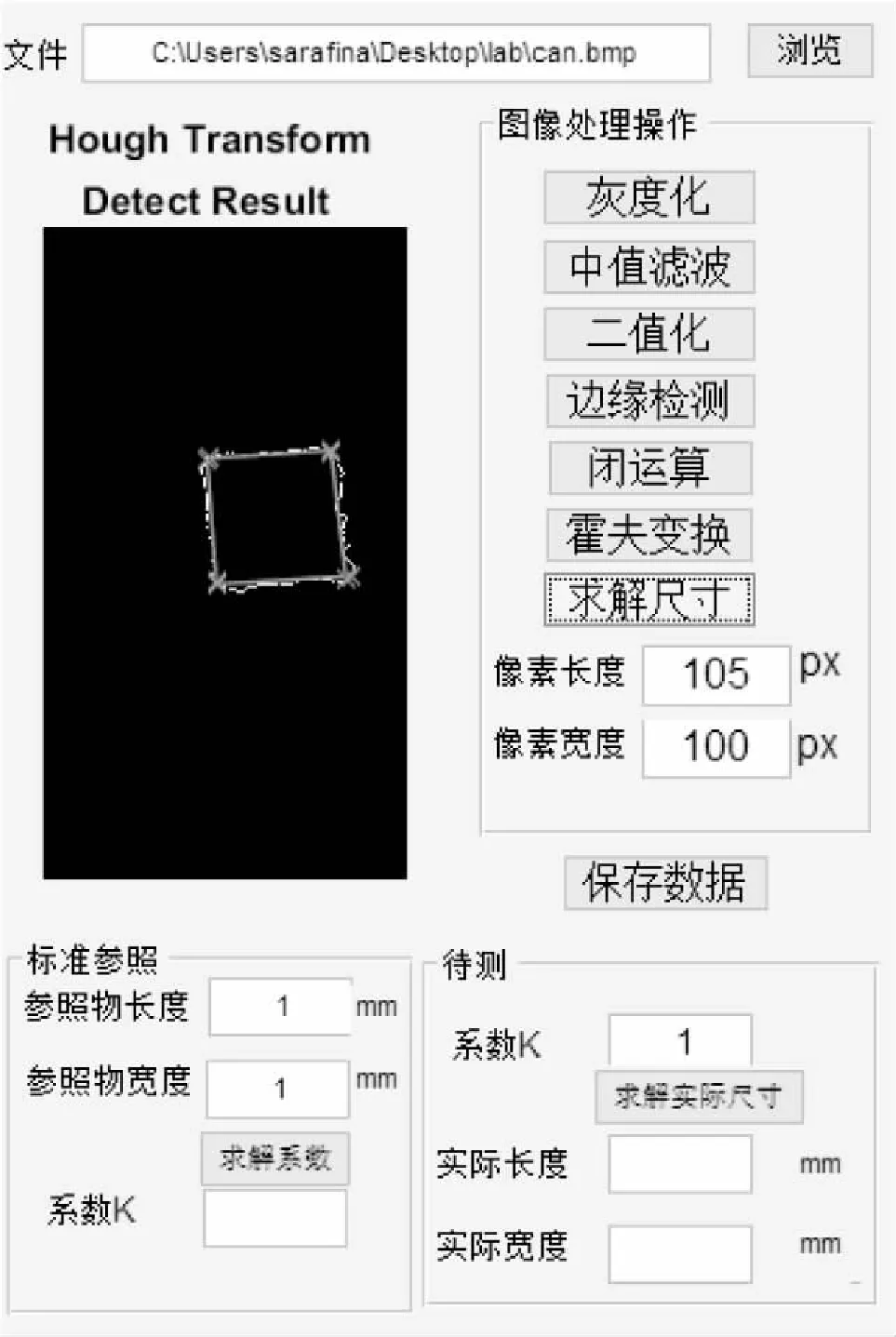
图4 系统界面图

原图分割出的目标区域如下，分割结果经过剪裁，去除了噪声、干扰区域，仅对目标区域进行检测。对目标区域分别进行最小外接矩形检测和霍夫变换检测，矩形标画与原区域对比如图5所示。

图5 目标区域检测

对于同一图像的分割同一区域图像，测量结果中最小外接矩形算法所求得的区域像素尺寸为108×108，霍夫变换所求得的像素尺寸为100×100。

最后需要将像素尺寸缩放成实际尺寸，这里应用了比例标定的方法，就是在确定图像采集系统的工作距离后，采集已知尺寸的标准元件的图像。对采集图像进行一系列图像处理分析，计算出标准元件的尺寸测量值。若标准元件的已知实际值为s，在图像测量系统中求出的测量值是S,可以求出缩放比例。而待测元件获得的测量值是l，则零件的实际长度可根据测量长度乘以缩放比例求得。为了提升系统标定的精确度，可执行多次标定求均值，得到最无偏的标定系数K[14]。然后图像分析算法所得的像素尺寸乘以标定系数K即可得实际尺寸。

从实际物体到结果数据的整个图像处理和分析过程是一个估计过程，不可避免地存在误差，可以分为系统误差和随机误差。影响测量的准确度的因素有许多，文中主要关注的是[15]：

(1)光学镜头分辨率。

(2)图像采集的采样密度；高准确度需要大过采样，不能仅仅根据采样定理选取采样率[16]。

(3)图像分割的算法；采用不同的分割算法或同一算法中选取不同参数时都会导致分割结果的变化。霍夫变换方法中主要有4个参数会对检测结果产生影响:角度范围、角度步长、ρ范围、ρ步长。最小外接矩形算法对检测结果产生影响的参数主要是角度步长α。

最小外接矩形理论上会较物体偏大，本质因为物体边缘会有一些毛刺，可以对区域图像进行开运算进行优化，但总体依旧会略微偏大。而霍夫变换所取得的矩形与区域较为接近，有较大的可能偏小，偏大的可能性比较小。实验中，物体的形状比较规则，所以使用霍夫变换的精度较高。而当形状不规则时，霍夫变换就无效了，所以最小外接矩形算法的应用范围广，适应度高，而霍夫变换的应用范围小，但是在可适用范围内的精度较高。

表1是分别使用直接传统测量、霍夫变换和最小外接矩形方法得到的估计值的统计数据。

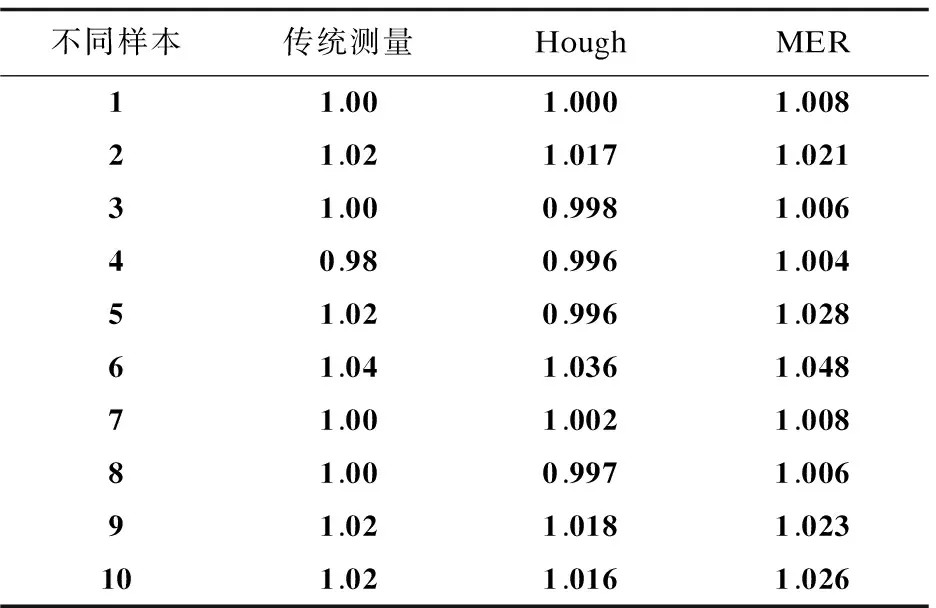
表1 不同算法的测量宽度结果对比 mm

3种计算方式得到的估计值的均值和方差如图6所示。

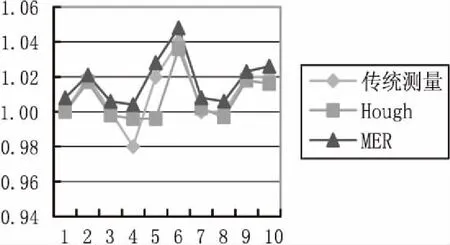
图6 测量结果对比图

如图6可得，传统测量估计值的均值是1.01；霍夫变化估计值的均值是1.0076，平均误差是0.59%；最小外接矩形估计值的均值是1.071，平均误差是0.76%。由此可见，在矩形度较高时霍夫变换相对于直接测量的误差较小，准确性较高，方差也较小。

6 结束语

设计实现了两种图像测量尺寸的算法，取得了不错的测量效果，实验结果证明了算法的正确性、可行性，并验证了这两种算法在尺寸上的有效性和互补性。下一步工作是增加算法的自适应性和并行性，使之可以在集群中工作，提高效率；并以尺寸特征作为分类属性，自动化地分辨合格品与非合格品。

[1] 章毓晋.图像工程[M].北京:清华大学出版社,2013.

[2] GONZALEZ R C,WINTZ P.Digital image processing[M].北京:电子工业出版社,2007.

[3] EKSTROM M P.Digital image processing techniques[M].[s.l.]:Academic Press,2012.

[4] 黄志坚，张金芳，徐帆江.关键点检测的线要素综合算法[J].中国图象图形学报,2012,17(2):241-248.

[5] 张大朴，李玉山，刘 洋，等.采用拟梯度方向信息的随机Hough变换直线检测[J].计算机科学,2006,33(4):208-210.

[6] 郭斯羽，翟文娟，唐 求，等.结合Hough变换与改进最小二乘法的直线检测[J].计算机科学,2012,39(4):196-200.

[7] 张 彤，刘 钊，欧阳宁.基于图形处理器的实时直线段检测[J].计算机应用,2009,29(5):1359-1361.

[8] SATHYANARAYANA S S,SATZODA R K,SRIKANTH-AN T.Exploiting inherent parallelisms for accelerating linear Hough transform[J].IEEE Transactions on Image Processing,2009,18(10):2255-2264.

[9] MUKHOPADHYAY P,CHAUDHURI B B.A survey of ho-ugh transform[J].Pattern Recognition,2014,48(3):993-1010.

[10] AGGARWAL N, KARL W C. Line detection in images through regularized Hough transform[J].IEEE Transactions on Image Processing,2006,15(3):582-591.

[11] FREEMAN H.Determining the minimum-area encasing rectangle for an arbitrary closed curve[J].Communications of the ACM,1975,18(7):409-413.

[12] JUNG C R，SCHRAMM R.Rectangle detection based on a windowed Hough transform[C]//Computer graphics and image processing.[s.l.]:[s.n.],2004:113-120.

[13] GONZALEZ R C,WOODS R E.Digital image processing (3rd Edition)[C]//IEEE international electric machines & drives conference.[s.l.]:IEEE,2013:1160-1165.

[14] JAVADI M,EBRAHIMI M.Fast width detection in corridor using Hough transform[J].International Journal of Image Graphics & Signal Processing,2012,15(2):179-187.

[15] 马艳娥,张波涛,高 磊,等.基于图像处理的零件尺寸测量研究[J].电子测试,2011(8):39-41.

[16] 张少军,艾矫健,李忠富,等.利用数字图像处理技术测量几何尺寸[J].北京科技大学学报,2002,24(3):284-287.