一种改进的OMP算法及其在图像重构上的应用

石曼曼，李 雷

(南京邮电大学 理学院，江苏 南京 210023)

0 引 言

传统的信号采样建立于奈奎斯特(Nyquist)定理上。其要求采样速度必须超过原始信号两倍频宽，才能恢复出原始信号。随着数字信号处理的迅猛发展，待处理的信号越来越多，导致传输的压力过大。因此，迫切需要一种全新的采样方式，去满足采集存储信息的要求。于是，压缩感知(compressed sensing,CS)[1-2]理论应运而生。

CS与奈奎斯特取样不同的是，它利用了信号更多的信息，包含稀疏性和相干性，不再受带宽的限制，实现取样、压缩一体化，不仅节省了存储空间，而且降低了元件损耗的风险。目前，CS广泛应用于遥感成像[3]、医疗成像[4]、无线传感网络[5]、雷达成像[6]等众多领域。

重构是CS技术关键的一步，主要有三大类方法[7]，包括最小l1范数的凸松弛算法、贪婪算法以及组合算法。凸松弛算法包含基追踪(basic pursuit,BP)算法[8]、基于梯度投影的一类算法[9]等等。贪婪算法基于最小l0范数，包含正交匹配追踪(orthogonal matching pursuit,OMP)[10]、正则化的正交匹配追踪(regularized orthogonal matching pursuit,ROMP)[11]以及压缩采样匹配追踪(compressive sampling matching pursuit,CoSaMP)[12]等算法。组合算法是通过分组测试实现快速重构。因每一类算法在重构耗时和重构结果上各有利弊，不少学者针对算法的各种缺点进行优化[13-14]。

贪婪算法凭借重构速度快的优势，得到了广泛的应用。其中OMP算法采用自下而上的方式更新，在未得到最终解时通过预设某个起始解，但是重构时间较长，重构精确度不高。OMP作为经典的贪婪算法之一，目前有很多学者对其进行了改进[15-17]。在此基础上，文中针对OMP算法重构时间慢、重构效果不好的缺点，加入双阈值，在OMP迭代至残差小于第一阈值后引入回溯思想，采用CoSaMP继续更新，直至残差小于第二阈值。将OMP的优点和回溯思想相结合，通过双阈值分阶段调控迭代，提出改进的双阈值分段迭代匹配追踪(DTSIMP)算法。

1 压缩感知理论

相比于奈奎斯特采样定理，CS利用观测矩阵直接得到可压缩或稀疏信号的特征信息。

假设x是一维离散随机信号，稀疏度为K，长度为N，即x∈RN×1。对于x，线性观测过程能用某个M×N维随机矩阵Φ表示(M≪N)，通过投影能够观测到M×1维列向量y，即

y=Φx

(1)

在这一过程中Φ是不变的，因此观测过程并非自适应过程。由式(1)可知，需要求解一个含M个等式的线性方程组。但由于M≪N，即方程个数远大于未知数个数，因此式(1)有无穷多解。若已知x的稀疏度为K≪M，也就是说x中含N-K个零项，同时已知位置，由CS知，这个欠定问题能够得到解决。只要观测矩阵Φ符合约束等距(restricted isometry property，RIP)[1]特征，即Φ满足下式：

(2)

其中，ε∈(0,1)，那么能够由y来获得K个稀疏观测。

将式(1)转化为l0范数极小化问题，求解得到原始信号，即：

(3)

在实际求解过程中，一般转化为次最优问题求解。即：

min‖x‖0s.t. ‖y-Φx‖2<δ

(4)

用贪婪算法求解此类问题，重构精度会略有降低，但缩短了运行时间，和其他类算法相比，具有更广泛的应用。

2 双阈值分段迭代匹配追踪算法

2.1 匹配追踪类算法

贪婪追踪匹配算法，采用多次迭代的思想，利用不同的特定准则实现迭代，最终通过特定的迭代终止条件，以观测矩阵作为原子库，从中判断筛选出能够准确表达原始信号的原子。由这些匹配原子经计算得到最优稀疏解。这类算法的最大特点是重构速度快，重建时间短。

OMP算法需要已知信号的稀疏度。在每一步迭代时，均从观测矩阵中选取与当前残差内积最大的原子，将其加入到支撑集，然后求解最小二乘，更新残差，进入下一次迭代。不妨假设信号是K稀疏的，则更新次数为K次。因为OMP算法在迭代中仅挑选唯一的原子来扩充支撑集，虽然得到的原子大部分是准确的，但会增大重构时间。且原子一旦并入支撑集，无论该原子是否准确，都只能保留。文中针对此缺点引入双阈值，并将迭代分为两部分，引入回溯思想，从而实现精准快速重构。

2.2 双阈值分段迭代匹配追踪算法

OMP算法每步更新只筛选出唯一原子加入支撑集，且加入的原子不能剔除，导致精度降低、耗时增加。而且作为一种经典的贪婪算法，其重构精度也有很大的提升空间。因此文中考虑改变OMP算法迭代的过程。为了不增加算法复杂度，第一阶段利用OMP算法迭代若干次，迭代停止阈值为α，然后引入回溯思想，利用CoSaMP算法更新，并将OMP更新所得残差和原子集当作第二阶段的输入值，第二阶段迭代停止阈值为δ，且δ<α，从而缩短重建耗时，实现准确重建。新算法步骤如下：

输入：观测矩阵Φ，观测向量y，信号稀疏度K，阈值δ；

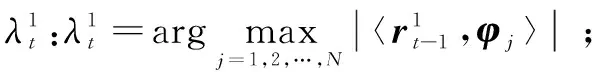
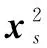
改进算法在残差不小于第一阈值α的条件下用OMP算法求解，之后引入回溯思想，采用CoSaMP算法迭代，用上一次更新得到的残差和原子集作为第二阶段初始值，并且通过第二阈值来终止迭代。且OMP算法迭代选择出的原子大部分是精确的，从而回溯过程开始时，会因为初始输入的精确性，使得信号得以快速重建，因此新算法是可行的。

3 实验结果和性能分析

给出不同算法的重构性能对比，以此分析算法的性能。实验对象为一维离散随机信号和二维图像。实验结果为各算法在相同实验条件下运行200次取平均所得。

3.1 重构性能分析

为了验证算法的有效性及优越性，在给定的采样率下，给出一维高斯随机信号的OMP与文中算法的重构成功率和重构时间与稀疏度的关系，并对仿真结果进行分析。

3.1.1 重构成功率分析

重构对象为一维高斯随机信号，长度N=256，测量矩阵Φ:M×N为高斯随机矩阵，分别用OMP算法和文中算法进行重构。第一阈值为α，第二阈值为δ，在大量实验基础下，均衡重构时间和精度，取α=6×10-3*‖y‖2，δ=10-5*‖y‖2。采样率取0.5时，两种算法在改变稀疏度的情况下，重构成功率如图1所示。

由图1可知，随稀疏度的增加两种算法的重构成功率均降低，但文中算法的实验结果优于OMP算法。和OMP算法相比，新算法重构成功率大幅提高。稀疏度为40时，用OMP恢复出x的成功率约为60%，但文中算法对x恢复的成功率仍接近100%；当稀疏度为50时，OMP算法对应恢复信号成功率小于20%，无法保证重构成功，但文中算法依旧有90%以上的重构成功率，可见新算法具备成功重建信号的优势。

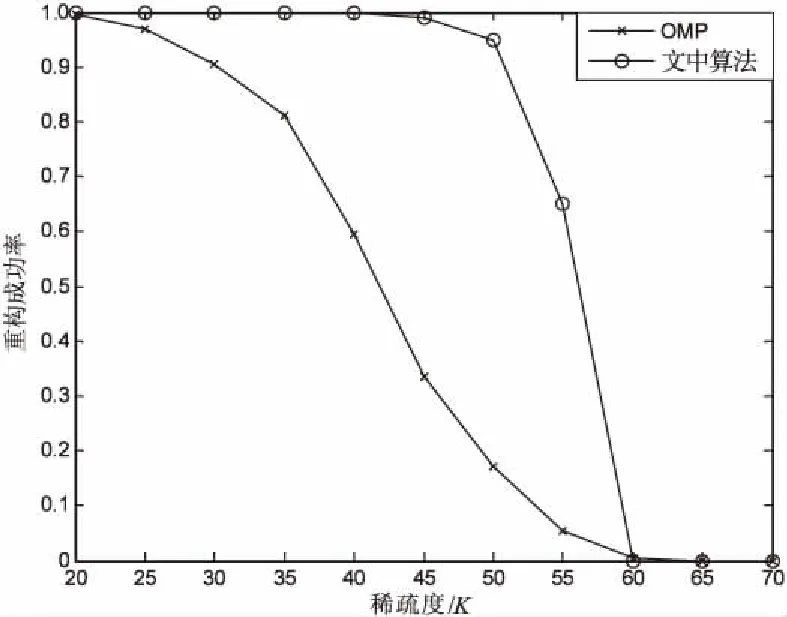
图1 重构成功率和稀疏度关系对比

3.1.2 重构运行时间比较

采样率相同时，给出文中算法和OMP算法重构所需时间与稀疏度的关系曲线，如图2所示，其中采样率取0.5。

图2 重构时间和稀疏度关系对比

由图2可知，稀疏度增大时，OMP和改进算法运行时间均有所增加，但新算法增加缓慢且重构时间比OMP算法少。这是因为文中算法采用双阈值两阶段迭代。首先，OMP算法迭代若干次之后，通过第一阈值控制进入第二阶段迭代；其次，引入回溯思想，使其快速正确地挑选原子，并由第二阈值约束控制，算法收敛时间变短。跟OMP算法比较，改进算法不仅具有很强的重构成功率，而且恢复速度快。

3.2 改进OMP算法在图像上的应用

将文中算法用于二维图像的重构，实验对象为256×256的Lena标准灰度图像。首先用DWT基对图像稀疏表示，之后用高斯随机矩阵线性观测，得到观测值，分别用三种算法重构，采样率取0.5，实验结果见图3。

由图3不难看出，文中算法的重建结果更接近原始图像，而OMP和CoSaMP重建的某些部分较为模糊，因此文中算法在图像上的重构也是可行且效果较好。

图3 重构效果对比图

表1和表2分别在采样率取0.5、0.6和0.7时，对比了不同算法的重构时间和峰值信噪比(PSNR)。

表1 重构时间和采样率的关系 s

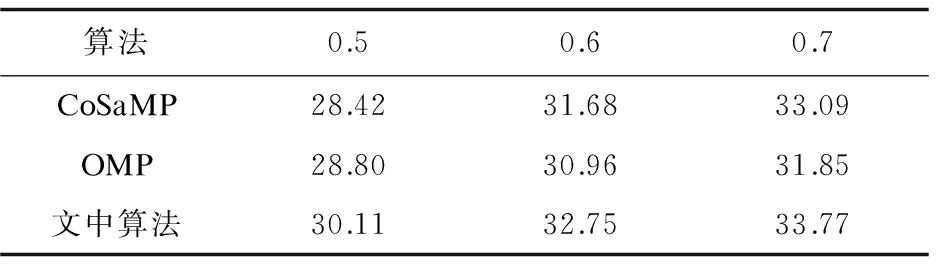
表2 峰值信噪比和采样率的关系 dB

由表1可知，随采样率的增大，三种算法重构时间变长，但文中算法在采样率相同时，耗时均最短，较CoSaMP算法耗时大幅减少，也比OMP算法平均快2 s，算法的速度快、耗时短。

由表2可知，随采样率的增加，PSNR增大，即图像恢复的更好。相同采样率时，文中算法的PSNR值略高于CoSaMP算法，且平均比OMP算法高出1 dB，重建结果最好。结合表1表明，文中算法重构性能更好。

4 结束语

提出了一种改进的OMP算法，利用双阈值两阶段控制迭代。首先利用OMP算法迭代若干次，至残差小于第一阈值时引入回溯思想，采用CoSaMP继续更新，残差小于第二阈值时停止迭代，从而精确快速地重构出稀疏信号。实验结果表明，与OMP算法相比，文中算法对一维的随机高斯信号和二维图像信号的重构成功率高，重构迅速且重构效果好。

[1] KUTYNIOK G.Compressed sensing:theory and applications[M].[s.l.]:Cambridge University Press,2012.

[2] 邵文泽,韦志辉.压缩感知基本理论:回顾与展望[J].中国图象图形学报,2012,17(1):1-12.

[3] 李烈辰,李道京.基于压缩感知的连续场景稀疏阵列SAR三维成像[J].电子与信息学报,2014,36(9):2166-2172.

[4] LIU Y,ZHAN Z,CAI J,et al.Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging[J].IEEE Transactions on Medical Imaging,2016,35(9):2130-2140.

[5] 黄海平,陈九天,王汝传,等.无线传感器网络中基于数据融合树的压缩感知算法[J].电子与信息学报,2014,36(10):2364-2369.

[6] 李少东,杨 军,陈文峰,等.基于压缩感知理论的雷达成像技术与应用研究进展[J].电子与信息学报,2016,38(2):495-508.

[7] 刘 芳,武 娇,杨淑媛,等.结构化压缩感知研究进展[J].自动化学报,2013,39(12):1980-1995.

[8] 张小亚,张 慧,王红霞.基追踪问题的近点算法及其应用研究[J].计算机工程与科学,2016,38(1):120-124.

[9] 张本鑫,朱志斌.全变差图像恢复的自适应步长梯度投影算法[J].自动化学报,2016,42(9):1347-1355.

[10] 刘记红,黎 湘,徐少坤,等.基于改进正交匹配追踪算法的压缩感知雷达成像方法[J].电子与信息学报,2012,34(6):1344-1350.

[11] NEEDELL D,VERSHYNIN R.Signal recovery from inaccurate and incomplete measurements via regularized orthogonal matching pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316.

[12] 蒋留兵,黄 韬.一种新的压缩采样匹配追踪算法[J].计算机应用研究,2013,30(2):402-404.

[13] 刘盼盼,李 雷,王浩宇.压缩感知中基于变尺度法的贪婪重构算法的研究[J].通信学报,2014,35(12):98-105.

[14] 陈善雄,何中市,熊海灵,等.一种基于压缩感知的无线传感信号重构算法[J].计算机学报,2015,38(3):614-624.

[15] 曾春艳.匹配追踪的最佳原子选择策略和压缩感知盲稀疏度重建算法改进[D].广州:华南理工大学,2013.

[16] 石曼曼,李 雷.基于分段可调节OMP算法的图像压缩感知算法[J].计算机技术与发展,2016,26(11):14-18.

[17] ZHANG D,ZHANG Y,HU X,et al.Fast OMP algorithm for 3D parameters super-resolution estimation in bistatic MIMO radar[J].Electronics Letters,2016,52(13):1164-1166.