基于遗传算法的多目标路径优化算法的研究

金仙力，李金刚

(南京邮电大学 计算机学院 软件学院，江苏 南京 210003)

1 概 述

车辆路由问题(VRP)可以描述为从一个或多个仓库中心到许多的地理位置分散的客户的行进路线的问题，此问题受制于许多方面的约束。VRP的目标是提供一套以最低成本的车辆路线完成客户交付的方案。

VRP问题在物流领域起着核心的作用。自从Dantzig和Ramser将VRP问题描述为旅行销售人员问题(TSP)以来，国内外的研究人员已经对VRP问题进行了大量的研究。例如简单的车辆路由问题(CVRP)，在此类问题中，任意一个客户对所需的商品都有要求，而且车辆的负载也有一定的限制；带时间限制的车辆路由问题(VRPTW)，在此类问题中，必须在一个特定的时间约束范围内访问每个客户；与装载和交付相关的车辆路由问题(VRPPD)，在此类问题中，必须以某个特定的数量装载和交付商品。

在静态VRP中，所有的客户在规划之前就已确定且不再更改。然而，常见的情况是，一旦服务已经开始，客户、服务时间或路由成本都可能会时时变化。由于定位系统和通信技术的最新发展，目前已经可以解决动态车辆路由问题(DVRP)了。

国内外的一些研究人员对DVRP进行了大量研究。比如，Montemanni等[1]对具有容量和持续时间约束的DVRP做了细化。这些研究人员不仅提出了DVRP的一些基准实例，而且进行了一个关于活动度如何影响最终成本的研究。此外，Montemanni等通过将DVRP分解为静态VRP序列，然后使用蚁群系统(ACS)算法求解问题，可以将DVRP视为标准VRP的扩展。Branchini等[2]提出了自适应粒度局部搜索启发式算法。Creput等[3]研究了将自组织图(SOM)神经网络操作为基于群体的进化算法的混合方法。Khouadjia等[4]研究了粒子群优化(PSO)和可变邻域搜索(VNS)。Elhassania等[5]将蚁群优化(ACO)算法和大邻域搜索(LNS)算法进行了新的混合。

基于静态VRP，可以研究许多不同版本的DVRP。例如，动态VRPTW被认为是一个标准问题，能很好地适用于允许对一组公共基准的启发式和元启发式的比较评估。为了解决这个问题，Housroum等[6]提出了一种进化方法；Hong[7]提出了一个改进的大型邻域搜索算法。此外还有其他各种DVRP的研究。Attanasio等[8]为动态多车辆拨号问题提供了一个平行的禁忌搜索启发式方法。Gendreau等[9]提出了邻居搜索启发式方法，以拾取和递送位置的实时新请求为基础优化车辆的计划路线。张迅等[10]研究了快递的同时送取货车辆路径问题(VRPSDP)，设计了一种优化算法，算法通过基于适应度排名和最优个体保留的选择策略和自适应交叉概率参数控制遗传算法，以保证所求结果的优良性。文献[11-16]中则是成功将遗传算法应用于解决各类VRP问题，为其他研究提供了有效的参考价值。薛明等[17]基于Small-World模型构建了云网格路网模型，实现了车辆的集成调度,提高了车辆运输效率。侯占亭[18]则是针对多个优化目标进行了研究，通过改进基于分解的多目标进化算法，实现了路径优化。于锐等[19]考虑了多种约束条件，比如时间约束、车载约束等，通过改进节约算法解决了开放式VRP。

综上。关于VRP问题的研究众多，但它们都有一个共同的问题，即服务点都是无序的。然而有些情况下，一些服务点是有顺序要求的，即必须按一定顺序为这些点提供服务。而在这方面的研究相对较少，因此文中的重点就是研究服务点有序的VRP问题。

2 DVRP问题的描述与建模

2.1 问题描述

以餐饮配送环境下的研究为目标，DVRP可以描述为：送餐人员从配送点出发到多个商家和客户进行取餐或送餐(对于同一订单，必须先取餐再送餐)，选择合适的送餐人员并合理组织其送餐路径，使送餐人员从配送点出发，能够合理地经过每个商家和客户点，并在满足每个商家和客户取餐量和送餐量的需求、送餐人员的承载限制以及商家和客户的时间限制需求等约束条件下，以最低的总成本为每个商家和客户提供服务。文中研究的问题属于DVRP，结合餐饮配送的特点，可以对问题做一些相应的假设，如下所示：

(1)只考虑单送餐人员，且具有载重量约束条件；

(2)送餐人员从配送中心出发，且送餐人员配送途中不接单，在服务点的取餐和送餐不消耗时间；

(3)每个服务点都会被访问，且只访问一次；

(4)商家服务点和客户服务点均有时间约束，超过这个时间就会产生惩罚；

(5)路径优化的目标：行驶成本最低，惩罚成本最低，总成本最低。

2.2 建立模型

(1)总成本最低化模型。

配送总成本包含三个部分，即不变成本、行驶成本与惩罚成本。其中不变成本包含车辆维护、送餐人员工资等，此成本是固定不变的；行驶成本则包含油耗等，此成本和行驶时间相关；惩罚成本是指因未在客户要求的时间内提供服务而产生的成本。

(2)行驶成本最低化模型。

行驶成本和行驶的距离相关。假设送餐人员行驶速度固定，则行驶距离和行驶时间线性相关，所以行驶成本也就和行驶时间相关。用n表示客户数量，tij表示送餐人员从客户i到客户j之间的行驶时间。可建立最低化行驶成本的数学模型如下：

(1)

决策变量：

(2)

(3)

其中，Xij为0表示送餐人员没有从服务点i到服务点j提供服务，Xij为1表示送餐人员从服务点i到服务点j提供服务；Yi为0表示送餐人员没有给服务点i提供服务，Yi为1表示送餐人员给服务点i提供服务。

约束条件为：

(4)

Yi=1

(5)

(6)

(7)

(8)

式(4)中，Pi表示服务点i的需求量，此式的含义是送餐人员的实际载重量小于或等于额定载重量Q；式(5)的含义是指每个服务点只能由一个送餐人员提供服务；式(6)、(7)表示送餐人员只能从一个服务点出发，并最终到另一个服务点去；式(8)的含义是必须要为每个服务点提供服务。

(3)惩罚成本最低化模型。

每个商家和客户都有时间约束要求，送餐人员必须在规定时间内提供服务，否则会产生时间惩罚。根据外卖配送特点，假定服务点i的时间约束要求为[0,Ei]，送餐人员到达服务点i的时间点为Ti，则可建立最低化惩罚成本的数学模型如下：

(9)

(4)综合总成本模型。

因固定成本不变，所以要使配送总成本最低化，只需考虑行驶成本与惩罚成本即可。可建立最低化总成本的数学模型如下：

Z=w1Z1+w2Z2=

(10)

其中，Z表示总成本；Z1表示行驶成本；Z2表示惩罚成本；w1、w2表示两种成本的权重值。

3 基于遗传算法的路径优化

3.1 遗传算法

遗传算法(genetic algorithm)是一种基于适者生存思想的算法。由于遗传算法采用随机化搜索，所以由遗传算法得出的结果存在一定的不确定性，即无法保证得到的结果是最好的结果。不过，通过一些改进方法，可以有效改善遗传算法的局限性，可以在可接受的代价下得到所需的结果。

3.2 遗传算法的设计

(1)染色体编码。

文中采用自然数编码，用1,2,…,n表示n个服务点。编码时，将两个“0”(代表配送中心)分别作为染色体的头部和尾部，如“0,1,2,3,0”，次染色体表示送餐人员从配送中心出发，依次经过服务点1、服务点2、服务点3，最终回到配送中心。

(2)产生初始种群。

最终解的优劣和初始种群有很大关系，因此初始种群的质量和规模要合理。为了得到一个比较合理并且能够较快收敛的初始种群，采用随机方法产生初始种群。即先得到[1,n]之间的所有整数，并打乱这些整数的排列，然后作为初始种群。

(3)计算适应度。

适应度是遗传算法中一个非常重要的因素，它是遗传算法进行遗传操作时的重要依据。因此一个科学合理的适应度计算方法能够有效地改善遗传算法，使之更加合理，更加高效。适应度的计算所遵循的规则也比较简单，即个体的结果越接近目标值，个体的适应度就越高。

(4)选择算子。

选择操作是从已知的种群中挑选出一个个体。因此，选择操作的优劣在一定程度上决定了遗传算法的优劣。选择操作以适应度为依据，因此适应度的计算非常关键。选择操作的结果往往是选择出适应度高的个体。

(5)交叉算子。

将选择出的个体，采用随机的方法进行匹配，产生一个完全不同的个体。具体操作方法为：随机在上一代个体中选择两个个体，并产生两个交叉段，将所选择的交叉段插入到另一个个体前端，并逐一去掉个体中与交叉段重复的染色体，以此得到新一代的个体。

(6)变异算子。

为了使种群更加丰富多样，可以执行变异操作。变异操作就是改变个体两个算子的位置。变异算法选择算子位置的方法是随机的，因此有一定的可能性会得到一个新的个体。

(7)调整算子。

结合餐饮配送的特点，即必须先到商家取货后才能给客户送货，需要对新产生的种群进行调整。将不满足条件的算子进行位置调整。

文中优化算法流程如下：

Step1：对客户点进行编码，并获得初始种群。

Step2：首尾插入0并标记适应度，获得一个种群。

Step3：对种群进行选择、交叉、变异、调整操作，获得新的个体。

Step4：若满足收敛条件，终止算法，否则进入Step2。

4 算法验证与分析

为了验证模型与算法的合理性与有效性，以南邮附近的外卖配送为例。假设配送员手中有5个订单，订单具体情况如表1所示。

如表1所示，每个订单包含商家地址、客户地址和时间窗信息。如1号订单，送餐人员要先到小马牛肉面取货，然后才能到学6宿舍送货，并且必须在15分钟内到达小马牛肉面和学6宿舍，否则将会产生时间惩罚。

表1 订单详情

假定配送中心为南邮大厦，根据以上订单信息，可整理出服务点的编号和地理位置、取货量、送货量和时间窗信息，如表2所示。

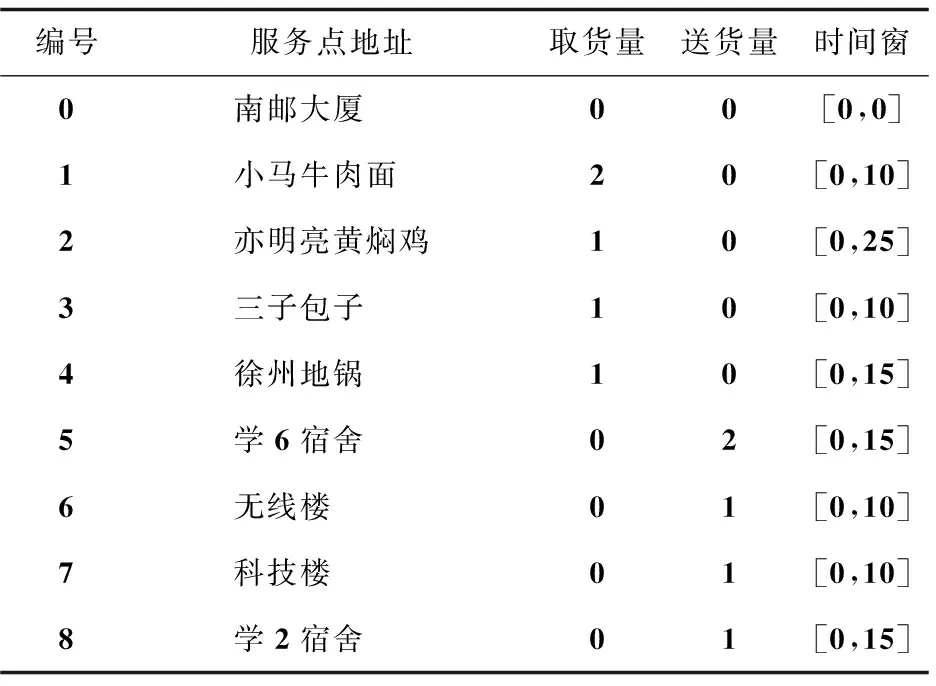
表2 服务节点的地理位置、取货量、送货量和时间窗信息

如表2所示，若服务点的取货量不为0，且送货量为0，则代表此服务点为商家；若服务点的取货量为0，且送货量不为0，则代表此服务点为下订单的客户。

为了计算总成本，需要知道每个服务点之间的行驶时间，从百度地图应用上可获取各个服务点之间的行驶时间，结果如表3所示。

表3 各个服务点之间的行驶时间 min

在表3中，每个编号代表一个服务点，其对应关系如表2所示。表3中的每个数据代表在两个服务点之间行驶所需要的时间。如4(第3行第4列)代表从编号1服务点到编号2服务点所需行驶时间为4min，即从小马牛肉面到亦明亮黄焖鸡需要行驶4min。

假设行驶成本的权重w1和惩罚成本的权重w2分别取值1和5，此时在WAMP上运行6次，所得结果如表4所示。

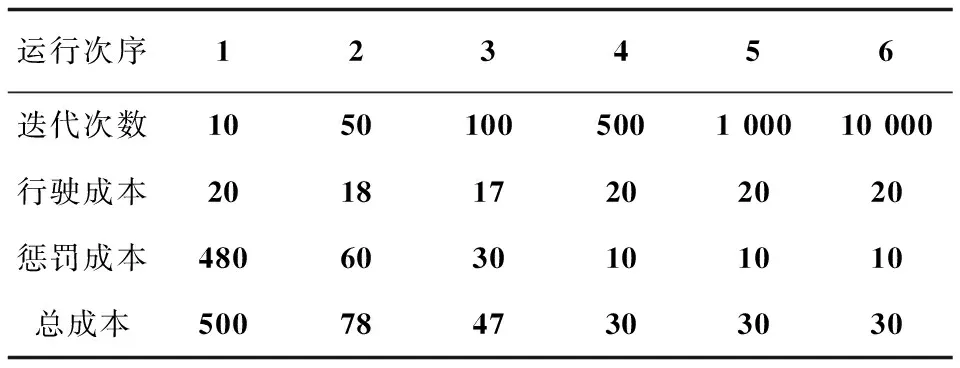
表4 运行结果

在表4中，迭代次数表示算法运行次数，当满足迭代次数时，算法会终止。此时，会出一个解集。由于遗传算法的特性，每次运行时，虽然迭代次数可能相同，但解集却可能不同，最终导致得到的解也可能不同。不过随着迭代次数的增加，得到的解会慢慢趋于一个稳定值。稳定后的解的总成本为30，其中行驶成本20，惩罚成本10。此时得到的路径为0231657480，即送餐人员送餐的路径为：南邮大厦-亦明亮黄焖鸡-三子包子-小马牛肉面-无线楼-学6宿舍-科技楼-徐州地锅-学2宿舍-南邮大厦。经验证结果有效。

和传统遗传算法做比较，它们的收敛情况如图1所示。

图1 算法收敛曲线

从图1中可以看出，文中算法的收敛速度明显高于普通的遗传算法，其收敛更快，效率更高，说明该算法有效、可行。

5 结束语

根据外卖配送的特点，提出了一种基于遗传算法的改进算法。基于外卖配送的实例进行了实验验证，表明该算法能够更快收敛，可以很好地解决服务点有序的VRP问题。

[1] MONTEMANNI R,GAMBARDELLA L M,RIZZOLI A E,et al.Ant colony system for a dynamic vehicle routing problem[J].Journal of Combinatorial Optimization,2005,10(4):327-343.

[2] BRANCHINI R M,ARMENTANO V A,LOKKETANGEN A.Adaptive granular local search heuristic for a dynamic vehicle routing problem[J].Computers & Operations Research,2009,36(11):2955-2968.

[3] CREPUT J C,HAJJAM A,KOUKAM A,et al.Self-organizing maps in population based metaheuristic to the dynamic vehicle routing problem[J].Journal of Combinatorial Optimization,2012,24(4):437-458.

[4] KHOUADJIA M R,SARASOLA B,ALBA E,et al.A comparative study between dynamic adapted PSO and VNS for the vehicle routing problem with dynamic requests[J].Applied Soft Computing,2012,12(4):1426-1439.

[5] ELHASSANIA M,JAOUAD B,AHMED E A.A new hybrid algorithm to solve the vehicle routing problem in the dynamic environment[J].International Journal of Soft Computing,2013,8(5):327-334.

[6] HOUSROUM H,HSU T,DUPAS R,et al.A hybrid GA approach for solving the dynamic vehicle routing problem with time windows[C]//Information and communication technologies.[s.l.]:IEEE,2006:787-792.

[7] HONG L.An improved LNS algorithm for real-time vehicle routing problem with time windows[J].Computers & Operations Research,2012,39(2):151-163.

[8] ATTANASIO A,CORDEAU J F,GHIANI G,et al.Parallel Tabu search heuristics for the dynamic multi-vehicle dial-a-ride problem[J].Parallel Computing,2004,30(3):377-387.

[9] GENDREAU M,GUERTIN F,POTVIN J Y,et al.Neighborhood search heuristics for a dynamic vehicle dispatching problem with pick-ups and deliveries[J].Transportation Research Part C:Emerging Technologies,2006,14(3):157-174.

[10] 张 迅,刘海东,李 丹,等.基于遗传算法的快递配送车辆路径问题研究[J].物流技术,2013,32(3):263-267.

[11] 王振锋,王 旭,葛显龙.基于遗传算法的不同约束条件车辆调度问题研究[J].计算机应用研究,2010,27(10):3673-3675.

[12] 袁麟博,章卫国,李广文.一种基于遗传算法-模式搜索法的无人机路径规划[J].弹箭与制导学报,2009,29(3):279-282.

[13] 邝航宇,金 晶,苏 勇.自适应遗传算法交叉变异算子的改进[J].计算机工程与应用,2006,42(12):93-96.

[14] 卢月品,赵 阳,孟跃强,等.基于改进遗传算法的狭窄空间路径规划[J].计算机应用研究,2015,32(2):413-418.

[15] 雷伟军,程筱胜,戴 宁,等.基于改进遗传算法的多模型加工路径规划[J].机械工程学报,2014,50(11):153-161.

[16] 庄 健,杨清宇,杜海峰,等.一种高效的复杂系统遗传算法[J].软件学报,2010,21(11):2790-2801.

[17] 薛 明,许德刚.基于云网格集成调度的防拥堵车辆路径规划算法[J].计算机科学,2015,42(7):295-299.

[18] 侯占亭.基于分解和决策空间相似性度量的进化多目标车辆路径规划算法研究[D].西安:西安电子科技大学,2014.

[19] 于 锐,曹介南,朱培栋.车辆运输路径规划问题研究[J].计算机技术与发展,2011,21(1):5-8.