两种改进的遥感影像地物分类方法对比研究
2018-03-05刘亮亮
刘亮亮,谢 菲,孟 鸣,2
(1.云南大学 资源环境与地球科学学院,云南 昆明 650000;2.云南省地理研究所,云南 昆明 650000)
0 引 言
遥感图像分割是对遥感图像内容理解和地物识别的关键技术,它可以将遥感图像的同质区域分离,使后续的分析和应用研究针对同质区域进行,有效提高了地物识别的精度和效率[1]。遥感图像分类识别的发展方向是使判别结果无限接近于实际地物,大量新技术新方法的不断研究与应用,将航空航天和卫星遥感上采集的数据信息经过加工处理,从宏观角度更为广阔地观察、理解和把握自己所赖以生存的这个星球。目前研究的遥感图像分类方法是对传统分类方法的重大改进,由于待分类的遥感图像都属于数字图像,而数字图像的分类是通过计算机来实现的。这种分类方法能充分利用遥感数据提供的各种统计信息,从理论上其分类结果必定是高度定量化的,可以精确到图像对应地面上的像元,容易进行面积统计[2-4]。做好图像分类以及分类后的处理工作,进行适当的人为释译,可以在节省经费、时间的同时,达到比经过人工解译、勾绘、转绘、量算和传统的统计方法结合处理后的分类精度更高的精度。随着传感器技术及计算机模式识别技术的不断发展,遥感图像由单波段发展到多光谱再到高光谱,遥感图像分类方法也得到了越来越深入的研究与应用[5-6]。
1 改进的贝叶斯最小错误率的遥感影像分类算法
贝叶斯最小错误率分类方法的设计初衷很简单,就是进行“分类”这一操作。为方便说明,令{ω1,ω2,…,ωc}表示有限个类别集,{a1,a2,…,aa}表示有限的a中可能采取的动作集,风险函数λ(ai|ωj)描述类别状态为ωj时采取行动ai所产生的风险[7-9]。
1.1 定义损失函数
已知使用贝叶斯公式可以通过先验概率P(ωj)、概率密度函数(似然函数)p(x|ωj)以及证据因子p(x)求出后验概率P(ωj|x):
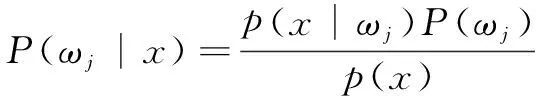
(1)
假设样本具有特征值x,并且将采取ai行动,而样本的真实归属类别为ωj,那么将可能造成损失λ(ai|ωj),而后验概率P(ωj|x)表示特征值为x时,样本属于类别ωj的概率,因此,与行为ai相关的损失为:
(2)
其中,R(ai|x)称为与行为ai相关的损失函数。
计算损失函数的步骤如下:
Step1:通过将特征值、似然函数、先验概率带入贝叶斯公式,求出具有特征值x的样本分属各个不同类别的可能性(后验概率);
Step2:将样本属于各个不同类别的可能性乘上将样本误判到这一类别所需付出的代价;
Step3:将Step2的结果相加即可得出对具有特征值x的样本进行ai操作所可能产生的损失。显然,要计算损失函数,先验概率、似然函数、风险函数都必须已知。
1.2 贝叶斯决策规则
为了最小化总风险,对所有的i=1,2,…,a计算条件风险R(ai|x),并选择行为ai使R(ai|x)最小化。最小化后的总风险值称为贝叶斯风险,记为R*,它是可获得的最优风险。
假设判决规则为函数a(x),它用来说明对于特征值x应采取哪种行为(即a1,a2,…,aa中选择哪种行为)。如果有一种规则,使得损失函数R(ai|x)对每个特征值x都尽可能小,那么对所有可能出现的特征值x,总风险将会降到最小[8-9]。而理想的规则就是贝叶斯决策:“对所有的i=1,2,…,a,计算条件风险R(ai|x),并选择行为ai使R(ai|x)最小化”。而在实际操作过程中,通常没有那么多已知条件,不过贝叶斯决策理论至少提供了一个与其他分类方法做对比的评价依据,也就是说贝叶斯决策很多情况下是作为对比对象而存在的。
1.3 影像分类改进判别函数的建立
针对遥感影像进行地物类型分类问题,首先定义一个风险评价函数:过程表现是wi类,判别为wj类时造成的风险为Lij;最小风险判别准则:选取j,使rj(X)最小。利用贝叶斯公式重新定义风险函数[10-12]:
(3)
如果r1(X)
设i类判为除i之外的地物时所承担的损失是0.11,判断正确时的损失是0,从而得到如下的判别公式:
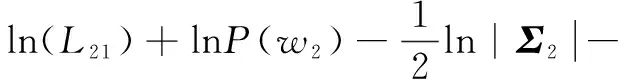
(4)
函数值达到最大时即得到所判定的地物类型,最后显示重新还原的RGB遥感图像。
1.4 遥感图像分类结果分析
图1为贝叶斯最小错误率算法的影像分割分类结果。

图1 贝叶斯最小错误率算法的影像分割分类结果
从整体来说,贝叶斯最小错误率算法将水体和陆地进行了很好的区分,对于大部分地物来说也进行了很好的分类,从视觉角度来看分类结果比较理想;但是从(c)、(d)两张分类结果的局部放大图来看,从视觉上具有相同色彩的部分耕地也被误分为水域,而且对于城市内部来讲,城市建筑物产生的阴影也对分类结果的准确性造成了很大的影响,而且对于细小的地物类型也都被归入了附近的地物大类之中。从统计学的角度来讲(见图2),水域约占影像整体分类的43%,耕地约占18%,居民点约占29%,耕地约占10%,而交通用地和未利用地约占不到总和的1%。
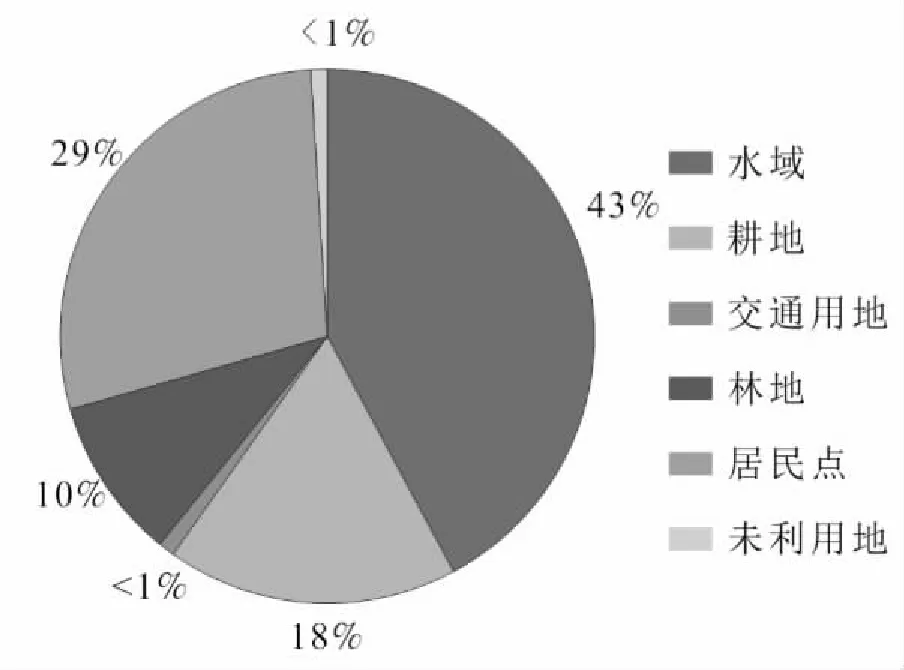
图2 改进的贝叶斯最小错误率算法的影像分类结果统计图
从上述例子可以看出,证据因子p(x)对函数做出哪种分类判断的结果没有实质性的决定作用,它的存在仅仅是作为一个标量,用来表示一种比例,即表示实际测量的具有特征值x的模式的出现频率[3]。如果把它去掉,也可以将判决规则改为:“如果p(x|ω1)P(ω1)>p(x|ω2)P(ω2),则判决为ω1类,否则为ω2类”。然后用贝叶斯公式来帮助做决策的大概思路,就是计算出某个特征值为x的待测样本属于各个不同类别的可能性,然后根据判断规则,选择概率最大(即可能性最大)的一个作为决策结果。
2 基于小波变换的改进K-mean算法的影像分类技术
K-means是一种广泛使用的基于划分的动态聚类算法。该算法以K为参数,把n个对象分为K个类别。根据一个类别中对象的平均值进行相似度计算,以达到使相同类别之间具有较低的相似度、类别之内具有较高的相似度的目的[10-13]。传统的均值-方差K-mean聚类算法有着不可避免的缺点:分类精度较低;由于初始聚类中心的选取具有随机性,初始值的选取会导致分类结果具有较大的差异性。
针对传统算法的缺点,提出了基于小波变换的改进K-mean算法。小波变换分析是一种基于应用数学理论的知识,其优势在于具有良好的时域频域局部化、尺度变化和方向选择性等特征,尤其近年来在纹理结构特征信息提取方面也有一定的应用研究[11]。文中采用Daubechies1小波,以云南省昆明市滇池流域海口镇遥感图像为分类目标,在非监督类方法基础上融合监督类方法的思想,对遥感图像进行小波变换,提取样本图像的纹理特征向量,同时将各类地物的样本图像纹理特征向量作为初始聚类中心;读取样本数据的纹理特征向量进行分类,并返回分类图像的RGB图,进行遥感图像分类,同时显示各类地物的面积比例。
2.1 样本纹理特征提取
当地物类型的光谱信息比较接近时,仅依靠光谱信息进行分类结果误差较大。在这种情况下,分类过程中可以引入纹理特征信息,因为不同地物的光谱特性可能相同,但是其纹理特征肯定存在明显的区别,所以就可以达到区分地物的目的。在计算机视觉研究领域,纹理是描述图像的一个重要特征,基于小波变换的纹理分割方法是一种理想的图像分割算法[13-14]。
设定小波包分解的层数为m,对Bi(i=1,2,…,p)分别进行m层二维小波包分解,对于每个图像子块,均得到4m个分解子频带图像。这里为了简便,决定进行单尺度的小波变换,m取1,共得到4个分解子频带的图像[5]。将每个图像子块的4个子频带的绝对值平均能量值作为一个特征分量,其表示为:
(5)
其中,M、N为子频带X的宽和高;X(i,j)为频带系数值。
因此第i个子块的特征向量为:
wi=[ei,1,ei,2,ei,3,ei,4]
(6)
其中,ei,k表示第k个子频带的平均能量值。
2.2 样本特征向量提取
通过下载的图像资料中如土地利用类型图和植被分布图等,根据图像各波段的光谱色调、纹理、形状等特征(见表1)在屏幕上直接选取有代表性的地物类型的区域。

表1 昆明市滇池流域遥感图像典型地物类型的目视解译标志
对待分类图像进行二维单尺度小波变换(DWT2),通过指定小波或者分解滤波器进行二维单尺度小波分解,提取特征向量。
2.3使用改进的K-mean算法进行遥感图像分类
实验分割对象为云南省昆明市滇池流域海口镇的2015年谷歌地球遥感图像(见图3)。算法在MATLAB.R2010a平台上实现,经过反复对实验区原始图像进行分割实验,选取迭代次数为25~30,可以获得较好的分割结果。

图3 小波变换改进的K-mean算法影像分割分类结果
按照各地物类型占总研究区的比例得到如图4所示的饼状图。
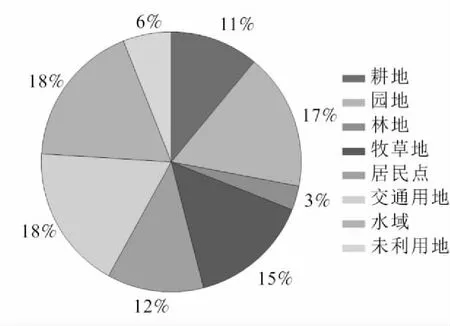
图4 K-mean算法分割影像分类结果统计图
2.4 遥感图像分类结果分析
根据海口镇土地利用总体规划2010年土地利用现状变更调查结果显示,全镇土地总面积为17 437.57公顷,已利用土地16 181.52公顷,占全镇总面积的92.80%,未利用土地1 256.05公顷,占总面积的7.20%,土地利用较为充分。在已利用的土地面积中,耕地为2 880.33公顷,占16.52%,林地10 690.97公顷,占61.31%,园地224.33公顷,占1.29%,居民点及工矿用地1 570.66公顷,占9.01%,交通用地为455.45公顷,占2.61%,水域用地184.38公顷,占1.06%。根据海口镇土地环境条件,规划前有零星牧草地约占1%,后期规划调整中不再配置增加牧草地。
分割性能评价误分率是指错误分割的像素占理想分割图像总的像素的百分比,误分率越低,说明对于被分割的图像其被错误归类的像素越少,即分割效果越好,归类越准确。反之,误分率越高,说明对于被分割的图像其被错误归类的像素越多,即分割效果越差,归类越模糊。将2015年的遥感影像分类结果和2010年海口镇土地利用现状变更调查结果进行对比(见图5),结果显示林地、园地、牧草地、水域以及交通用地影像自动分类结果和调查数据差距较大,误分率均达到70%以上。但同时在对园地、林地、牧草地提取图像特征时,三种地物类型具有明显的相似性,包括颜色和外表轮廓等,如将三者进行合并进行统计分析,则误差率降低为35.5%,则分类结果较为可信。按照海口镇经济发展趋势进行分析,2015年的全镇经济水平明显高于2010年,部分耕地、未利用土地转化为居民及交通用地是经济发展中一个不可避免的趋势,因此对于耕地、未利用地以及交通用地的变化可以认为分类结果准确,误差在合理的波动范围之中;对于水域分类结果的差异则是由于2010年进行土地利用现状变更调查中统计的水域面积扩大以及由于遥感影像的图像色阶差异导致误分,也是后续研究中需要解决的一个问题。
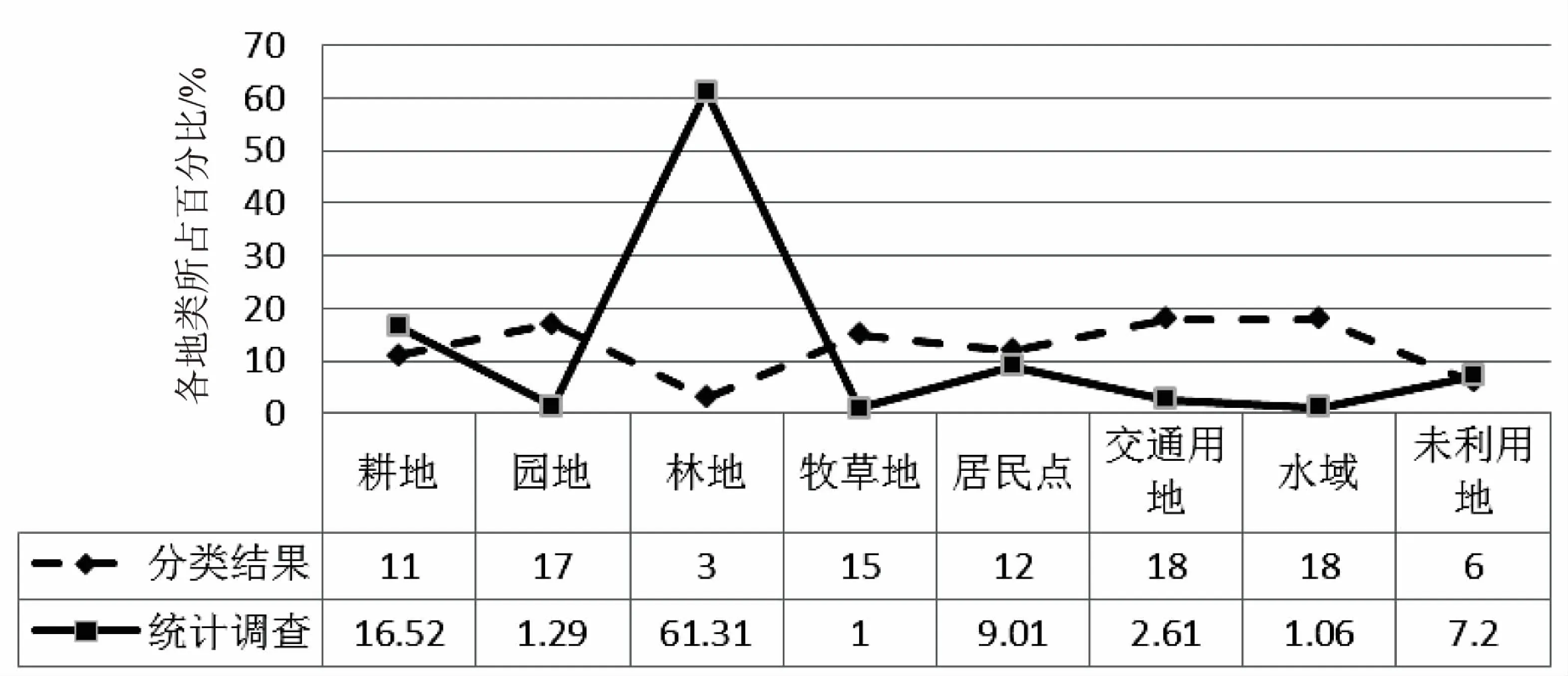
图5 遥感影像分类结果和调查结果对比图
总体来说,从统计以及人工识别的角度进行综合分析,利用该算法进行的遥感影像自动分类结果较为可信,如能获取更加精确的土地利用类型数据,则影像总体分类精度将会进一步提高且更加可信。
3 结束语
上述两种算法的实验仿真结果表明,经过改良的小波纹理分割遥感影像计算方法能够清晰地对高分辨率遥感图像进行分割,待分类图像经过单尺度二维离散小波变换后,削弱了相同地物类型内部的噪声,提高了不同地物类型的边缘差异性[15];而贝叶斯最小错误率分类方法在大范围调查中且不追求高精度的统计数据时有很好的利用前景,而基于小波变换的K-means算法对于精确数据统计应用效果较好。文中方法尽管能够完成大部分图像的分割以及分类研究,但是在实验过程中也发现,对于图像中的个别区域以及阴影区
域出现了较大的误差,误分概率较大,所以算法还存在很多不足之处,需要加强。对于实验结果中图像分类效果好坏的评价是通过目视观察和来自官方的统计数据进行对比分析,这种评价方法不仅费时而且常带有人的主观因素,因此,该领域迫切地需要一种好的图像分割方法评价标准。
[1] 侯立华.图像分割方法综述[J].科技创新导报,2008(22):249.
[2] 黄 煌,肖鹏峰,王结臣.多尺度归一化割用于遥感图像分割[J].遥感信息,2015,30(5):20-25.
[3] 谢娟英,高红超.基于统计相关性与K-means的区分基因子集选择算法[J].软件学报,2014,25(9):2050-2075.
[4] 王晓年,冯远静,冯祖仁.一种基于主动轮廓模型的蚁群图像分割算法[J].控制理论与应用,2006,23(4):515-522.
[5] 胡建强,李涓子,廖桂平.一种基于多维服务质量的局部最优服务选择模型[J].计算机学报,2010,33(3):526-534.
[6] CHAKRABORTY R S.Hardware security through design obfuscation[D].USA:Case Western Reserve University,2010.
[7] DORIGO M,BLUM C.Ant colony optimization theory:a survey[J].Theoretical Computer Science,2005,344:243-278.
[8] 曹永春,蔡正琦,邵亚斌.基于K-means的改进人工蜂群聚类算法[J].计算机应用,2014,34(1):204-207.
[9] 翟东海,鱼 江,高 飞,等.最大距离法选取初始簇中心的K-means文本聚类算法的研究[J].计算机应用研究,2014,31(3):713-715.
[10] WANG X,DU J,WU S,et al.Cluster ensemble-based image segmentation[J].International Journal of Advanced Robotic Systems,2013,10:297-308.
[11] 张亚利,睢 丹.改进小波算法在图像分割技术中的应用[J].数字技术与应用,2016(3):137-138.
[12] 赵 越,周 萍.改进的K-means算法在遥感图像分类中的应用[J].国土资源遥感,2011,23(2):87-90.
[13] 季 虎,孙即祥,邵晓芳,等.图像边缘提取方法及展望[J].计算机工程与应用,2004,40(14):70-73.
[14] 白 杨,孙 跃,王 君,等.基于动态自适应蚁群算法的MRI图像分割[J].计算机科学,2008,35(2):226-229.
[15] NEZAMABADI-POUR H,SARYAZDI S,RASHEDIE.Edge detection using ant algorithms[J].Soft Computing,2006,10(7):623-628.
