Magnus效应动力演示仪
2018-03-03王志鹏王四海
王 仿,李 昊,英 模,王志鹏,王四海
(北京邮电大学 a.软件学院;b.信息与通信工程学院c.计算机学院;d.理学院,北京 100876)
虽然Magnus效应已发现100多年,但真正深入地开展应用研究只是在近十几年[1]. Magnus效应曾被用来借助风力推动船舶航行,用几个迅速转动的铅直圆柱体代替风帆. 试验是成功的,但由于不经济,所以未被采用. 20世纪出现了大量的关于Magnus力的应用,尤其是在船舶上,如转柱舵、风筒推进装置、Magnus螺旋桨、Magnus减摇装置等. 这些装置增加了能源利用率,主要因为Magnus效应能够利用某方向上的流体动能在其正交方向上产生力. 足球、排球、网球以及乒乓球等的侧旋球和弧圈球的运动轨迹之所以有大的弧度也是起因于Magnus效应[2]. 为了获得更直观、更形象的Magnus效应效果,设计并制作了演示仪.
1 Magnus效应
Magnus效应以发现者Magnus命名,当旋转物体的旋转角速度矢量与物体飞行速度矢量不重合时,在与旋转角速度矢量和平动速度矢量组成的平面相垂直的方向上将产生横向力,在横向力的作用下物体飞行轨迹发生偏转的现象称作Magnus效应. 旋转物体之所以能在横向产生力的作用,是由于物体旋转可以带动周围流体旋转,使得物体一侧的流体速度增加,另一侧的流体速度减小[3].
根据伯努利定理,流体速度增加将导致压强减小,流体速度减小将导致压强增加,这样就导致旋转物体在横向的压力差,并形成横向力. 同时由于横向力与物体运动方向相垂直,因此该力主要改变飞行速度方向,即形成物体运动中的向心力. 用位势流理论解释,则旋转物体的飞行运动可以简化为“直匀流+点涡+偶极子”的运动,其中点涡是形成升力的根源. 在二维情况下,旋转圆柱绕流的横向力用儒可夫斯基定理来计算,即横向力=来流速度×流体密度×点涡环量[4].
2 实验仪设计
Magnus原理图见图1,旋转的转子会带动周围的空气旋转形成1层均匀环流,如果在此基础上叠加直匀流就会造成转子两侧产生速度差,由伯努利方程,就会产生压强差,从而产生Magnus力. Magnus力本质上是通过转子的旋转利用流体的动能产生在其正交方向上的力.
演示仪实体模型见图2,小车中间是转子,左边是涵道风扇. 转子利用软件3D建模,将质量减小到最小,然后3D打印,目的是保证筒壁各个部位都均匀;另外,由于制作工艺很难保证转子质心在几何中心,在内壁上同一高度均匀贴上4块小磁铁,再把其他小磁铁按照不同的分配方式吸上去,通过观测转子旋转时的抖动程度判断哪种搭配方式能够达到目标. 转涵道风扇用于模拟自然风. 通过遥控器可以控制转速和风速从而控制产生的Magnus力的大小. 为使演示效果达到最好,设计时让小车空间利用率最大,并且用稳压源供电,避免空间和重量的赘余. 现在小车能够在Magnus力的驱动下以较快的速度做直线运动,演示效果比较直观.

图1 Magnus原理图

图2 演示仪实物俯视图
在不影响演示效果的前提下,尽可能准确地采集物理参量.
1)风速仪:风力使得风速仪上面的螺旋桨受力转动,产生变化的磁场,霍尔传感器输出信号,经过计算模块显示为风速V风.
2)转速仪:转速仪发出激光,转子某处贴反光纸,当激光经过反光纸反射回转速仪时输出信号,经过计算模块可以算出转速n.
3)拉力传感器:内部为惠斯通电桥,当其中的电阻应变片受到压力F,长度或横截面积发生改变,使得输出电压线性改变,通过定标可以得到电压-压力曲线. 实验用的传感器200 g,如果输入电压是5 V,那么满量程输出电压为5 mV,初始电压可能有略微的系统误差,不过可以消除.
转速是通过激光仪接受由贴在转子上的反光纸反射回来的周期信号计算得到,然后近似到十位. 风扇输出口风速的分布是不均匀的,所以将风速仪固定在某位置. 至于F,已经尽可能地消除了误差,比如通过斜面来平衡阻力,避免在曲线中出现阈值的情况;在压力传感器上固定1根铁棍,铁棍的两端引出尼龙扎带与小车进行连接,两点接触能够较大程度地避免在实验中小车前进的方向发生变化. 通过上述改进示数已经比较稳定,但是还是存在波动,主要来源于转子和风扇的电机产生的噪声,只能在示数的波动中取平均值.
3 实验结果与分析
先测量不同V风下不同n对应的F,再测量相同n下不同V风对应的F.
1)不同V风下F与n的关系
根据儒科夫斯基定理,得到的曲线应该是若干条斜直线,但是从实验结果(图3)来看,除了V风=11.9 m/s的曲线基本正相关,其他曲线都存在极大值,所以猜想,当V风小于某个值时,曲线就会出现极大值. 将下面几条曲线的极值点标出,发现随着V风的增加,极值点右移,而且经过拟合,发现极值点近似满足nR=2.25V风,图3中蓝色点为实际极值点,竖线为据此式计算出的极值点,非常接近. 据此,猜测11.9 m/s曲线也应该存在极大值,只是实验域太小没有将极大值显示出来.
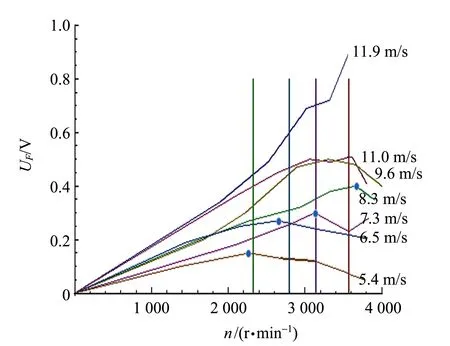
图3 不同V风时F与n关系图
2)不同n下F与V风的关系
同样,理论上得到的应该是若干条斜直线,而实际情况中上部若干条曲线都近似满足正相关(图4),唯独n=1 210 r/min曲线出现极大值,所以同样推测,当n小于某个值时曲线会出现极值. 但是由于实验中只看到极大值点,所以没法推测极值点和n与V风的关系.

图4 不同n时F与V风关系图
3)F与nV风的关系
由得到的散点图线性拟合,如图5所示. 尽管散点的离散度很大,但是拟合直线截距很小,基本近似于1条正比例直线,这和理想情况是相吻合的.
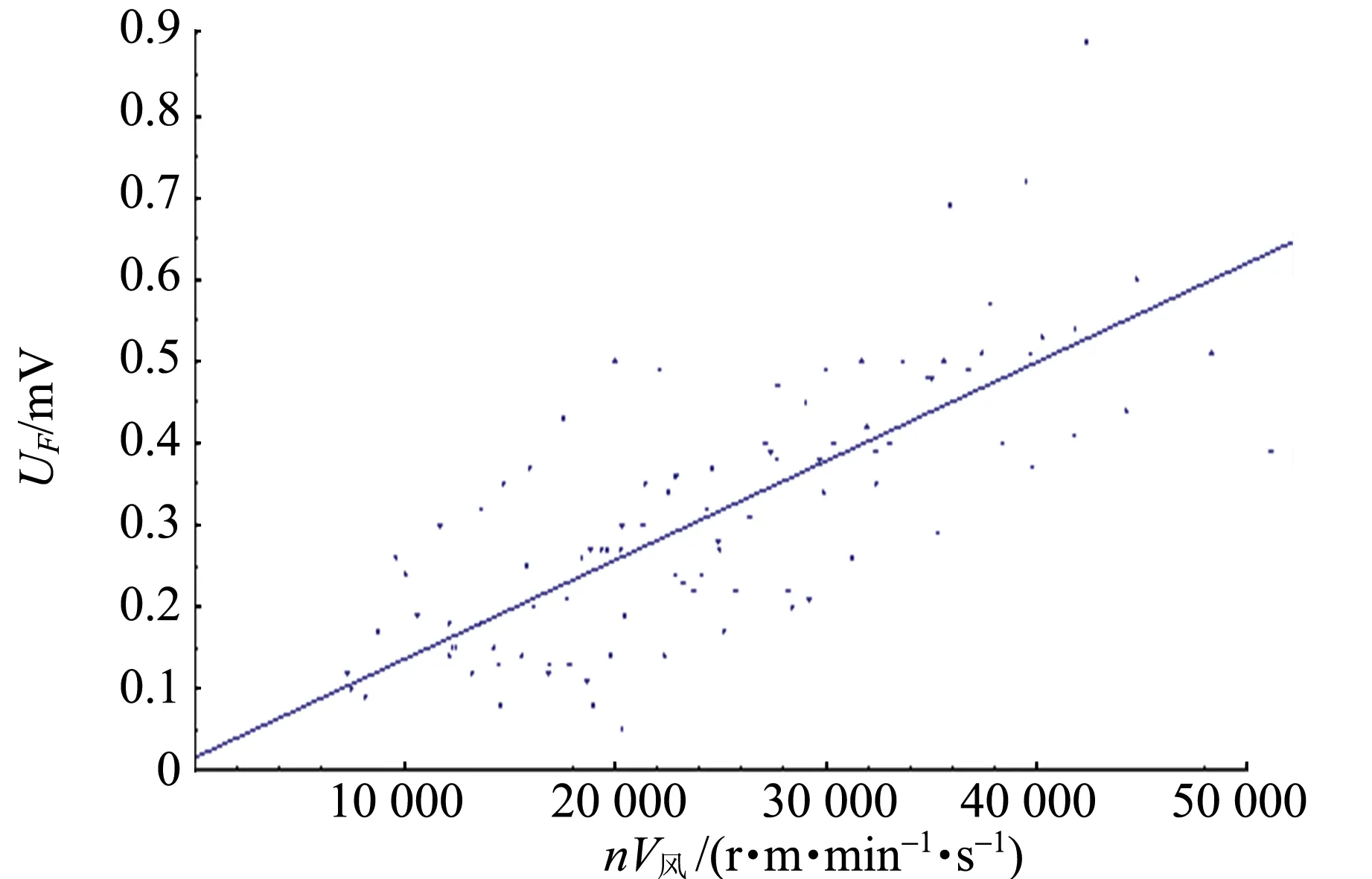
图5 F与nV风关系图
4 结束语
Magnus效应动力演示仪可以使运动生物力学在流体课的教学上获得更直观、更形象的效果. 就理论研究方面,实际工程中有很多基于Magnus的应用,但是应用中普遍错误地认为要想产生更大的Magnus力,只要增加V风或者n就可以了,但是实验证明了当V风或者n增加到一定程度时反而会使F减小,并且通过实验能够计算出如何控制2个变量得到F的最大值,有助于工程上确定变量范围.
[1] 彭东升. 马格努斯效应及其在船舶上的应用[J]. 江苏船舶,1990(2):23-25.
[2] 吴望一. 中国大百科全书74卷(物理学)[M]. 2版. 北京:中国大百科全书出版社,2009:352.
[3] 吕逢娇. 马格努斯效应在流量仪表上的应用[J]. 大学物理实验,2013,26(2):48-50.
[4] 张兆顺,崔林香. 流体力学[M]. 3版. 北京:清华大学出版社,2015:184.
