基于旋量理论的仿人机械臂正运动学与可操作性分析*

李文威 周广兵,2 陈再励 吴亮生 黄炜聪 陈惠纲



基于旋量理论的仿人机械臂正运动学与可操作性分析*

李文威1周广兵1,2陈再励1吴亮生1黄炜聪1陈惠纲1

（1.华南智能机器人创新研究院 2.广东省智能制造研究所）

为研究仿人机械臂的运动性能，采用旋量理论对SRU构型仿人机械臂进行正运动学与可操作性分析。首先基于指数积公式对机械臂进行正运动学分析，获得通用的正解解析式；其次基于运动旋量计算机械臂的雅克比矩阵，并通过雅克比矩阵获得机械臂操作空间中任意一点的全局相对可操作度；最后以某六自由度仿人机械臂为算例，对该机械臂进行正运动学和可操作性分析，给出可视化计算结果。

仿人机械臂；旋量理论；正运动学；指数积；雅克比矩阵

0 引言

D-H参数法和基于旋量理论的指数积（product of exponential，POE）公式是机器人运动学分析的2种重要方法，并在机械臂的运动学分析中广泛应用[1-2]。

D-H参数法需要针对每个杆件建立局部坐标系，然后在局部坐标系下，基于杆件的4个参数建立相邻杆件间的位姿变换矩阵，继而以首端到末端一系列变换矩阵的乘积表示机器人的末端位姿。D-H参数法建模过程复杂，当局部坐标系建立不恰当时，易产生奇异性；当自由度增多时，易形成累积误差。

应用基于旋量理论的POE公式进行机械臂的正运动学分析，基本过程是：1）分别在机械臂的基座和末端建立基坐标系和工具坐标系；2）在基坐标系下，确定机器人的初始位姿、关节的位置向量和轴向量；3）将关节位置向量和轴向量变换为运动旋量；4）通过POE矩阵指数连乘形式表达机械臂的末端位姿。可见，机械臂末端位姿误差只来源于位置向量和轴向量，可从根本上避免奇异性和累积误差的产生。

采用旋量理论建立的机械臂运动学分析模型不仅具有形式统一、描述简洁的优点，并且可应用在更深入的理论分析中，如，兰陟等采用旋量理论计算了五自由度机械臂的雅克比矩阵[3]；Zhu S等采用旋量理论对串联机械臂进行了动力学分析[4]。

1 正运动学分析

正运动学分析是给定各关节角，求机械臂末端位姿的一类问题。一种六自由度仿人机械臂的初始位姿状态及其结构参数如图1所示。该机械臂具有类似人臂的SRU（球面副-转动副-万向节副）串联构型，其构型特点为：1）前3个自由度正交于一点，其肩关节等效于一个球面副（S）；2）肘关节为转动副（R），只有1个自由度；3）后2个自由度正交于一点，其腕关节等效于一个万向节副（U）。这种具有类似人臂结构特征的仿人机械臂能够较好地模拟人臂运动[5]。

图1 SRU构型仿人机械臂的结构参数

在图1的基坐标系下，机械臂末端的初始位姿齐次矩阵为

按图1所示位置，计算各自由度的运动旋量坐标，所得结果整理后列于表1中。

表1 各自由度的运动旋量坐标

将机械臂各自由度的运动旋量坐标表示为

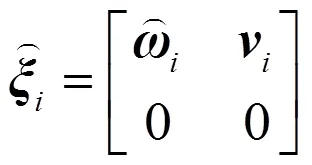
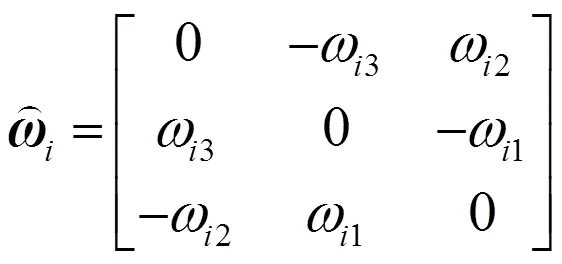
根据旋量的POE原理，目标位姿为

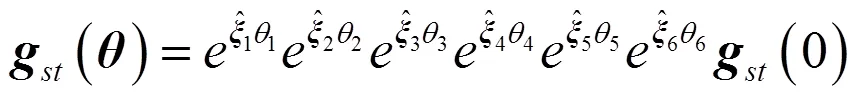
根据指数映射关系

可计算得到运动学正解计算式为

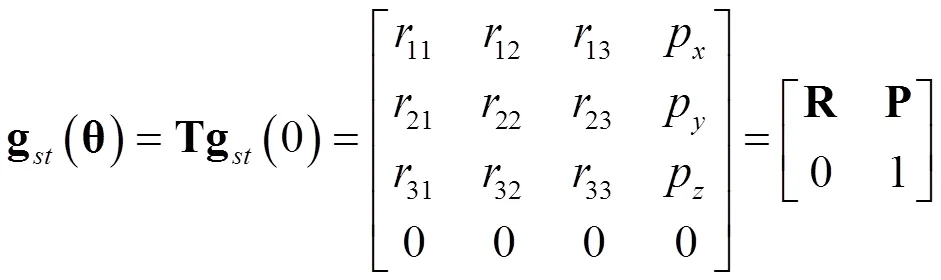
以符号运算形式在Matlab中编写运动学正解计算程序，得到式(5)中各元素的解析式为

11=6{5[4(13+123) –214] –5(13–

312)} –6[4(13+123) +241]

12= –6[4(13+123) +241] –

6{5[4(13+123) –214] –

5(13–312)}

13=5[4(13+123) –214] +

5(13–312)

21=6{5[4(31–123) +124] –5(13+

132)} –6[4(31–123) –124]

22= –6[4(31–123) –124] –

6{5[4(31–123) +124] –

5(13+132)}

23=5[4(31–123) +124] +

5(13+132)

31= –6[5(24+243) +235] –

6(42–234)

32=6[5(24+243) +235] –

6(42–234)

33=235–5(24+243)

p= –121–2241–2134–21234

p=112+2124–2314+21234

p=0–12–242+2234

其中，C= cosθ；S= sinθ。

2 可操作性分析

对于机器人来说，可操作性反映了整个系统对力和运动的全局转换能力，也就是机器人在任意方向上的运动和施加力的能力[6]。

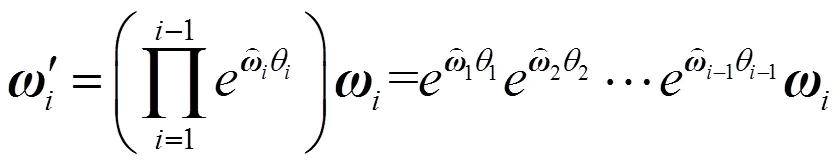
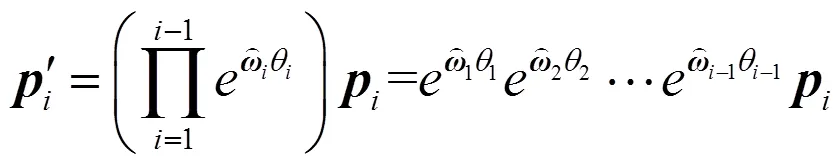
以求出的雅克比矩阵为基础，可进一步求得经过归一化处理的空间点全局相对可操作度[5]：

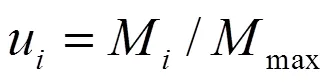
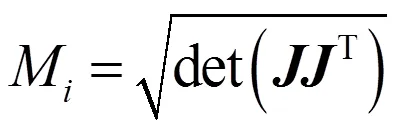
3 算例

为检验本文推导的运动学正解和可操作度计算式的正确性，以结构参数为(0,1,2)T= (0.15 m, 0.25 m, 0.25 m)T的仿人机械臂为实际算例进行验证。

首先，以特殊位姿验证正运动学分析结果的正确性。给定一组关节角(1,2,3,4,5,6)T= (0, 0, 0,–π/2, 0, 0)T，根据式(5)可计算得到末端位姿为

与式(13)对应的机械臂位姿的仿真效果如图2所示，可见，该位姿与机器人的实际末端位姿一致，说明正解计算正确。

采用蒙特卡洛法随机抽取机械臂关节空间内10000个点；再根据正运动学计算式(5)求出机械臂操作空间内相对应的10000个空间点坐标；最后利用式(7)~式(12)求出各空间点对应的全局相对可操作度值。经计算，机械臂工作空间内可操作度的最大值max= 0.0372。

为使机械臂操作空间内的全局相对可操作度的分布以可视化的方式呈现，在每个空间点位放置一个小圆球，并以圆球的直径代表u值的大小，所得机械臂操作空间内的可操作性分布如图3所示。由图3可见，机械臂的操作空间大致呈椭球型，椭球的外表面、中心点及上下顶点等极限位置附近可操作性较差。表2列出了机械臂操作空间内若干点位的全局相对可操作度数值。

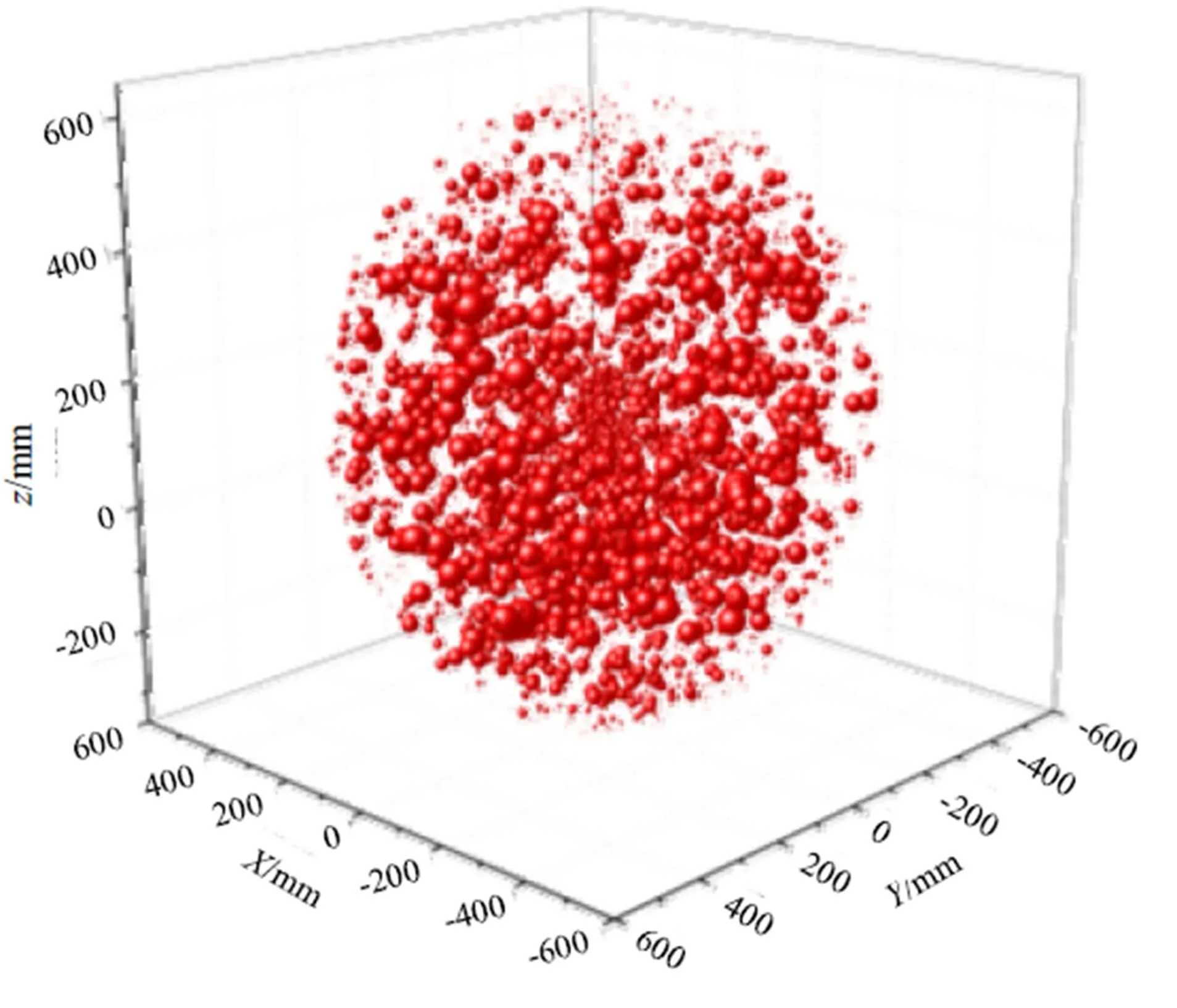
图3 机械臂操作空间内的可操作性分布

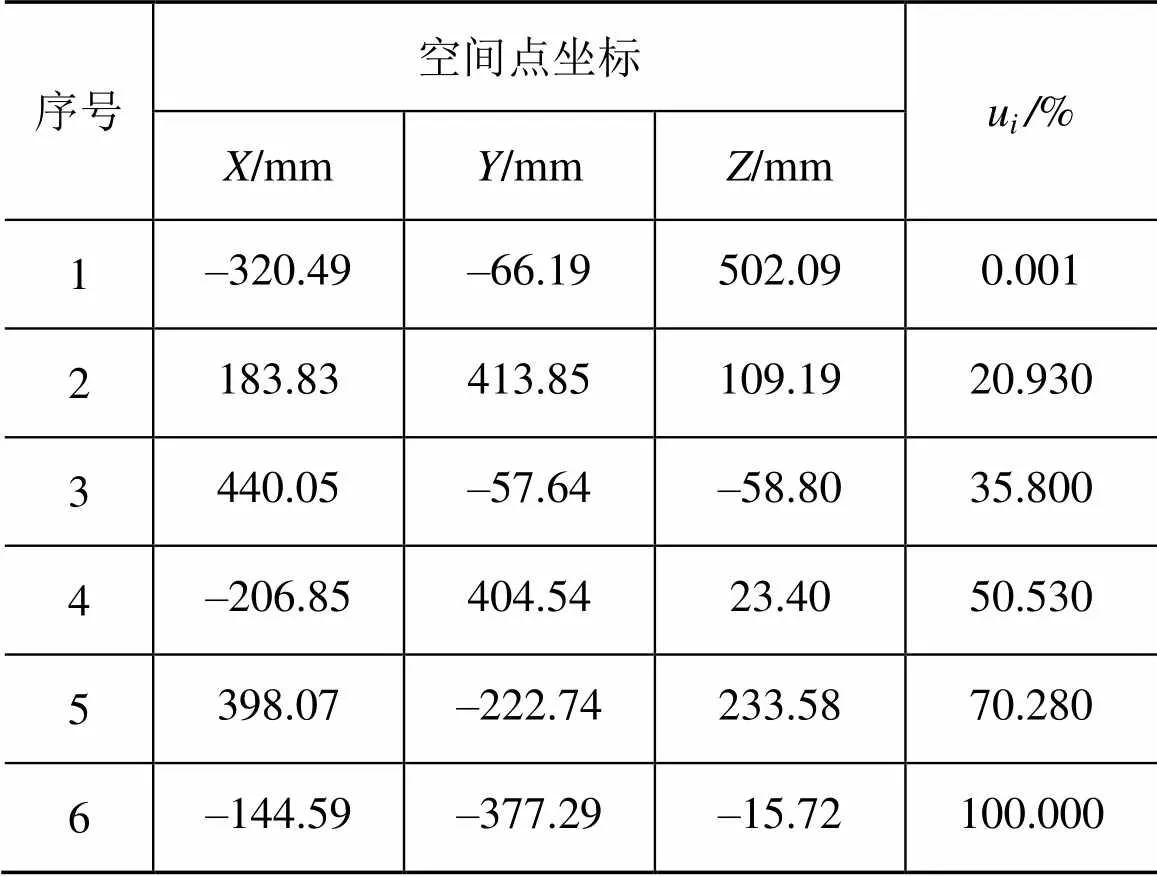
表2 机械臂操作空间内若干点位的全局相对可操作度

4 结语

基于旋量理论研究机械臂的运动性能，具有几何意义明确、表达形式统一和编程计算简便等优势。本文基于旋量理论推导了SRU构型仿人机械臂的运动学正解与全局相对可操作度的解析计算式，并针对一给定尺寸参数的六自由度仿人机械臂进行了相应的数值计算，文中的计算过程与所得结论对相似构型机械臂的运动性能分析具有一定的参考意义。后续将进一步研究运动旋量中包含随机误差时，仿人机械臂运动学性能的变化规律，并据此分析影响机械臂运动精度的关键因素。

[1] 朱齐丹,王欣璐.六自由度机械臂逆运动学算法[J].机器人技术与应用,2014(2):12-18.

[2] Kevin M L, Frank C P. Modern robotics: mechanics, planning, and control[M]. Cambridge: Cambridge University Press, 2017.

[3] 兰陟,李振亮,李亚.基于旋量理论的5-DOF上肢康复机器人雅克比矩阵求解[J].机械设计,2011,28(5):51-53,74.

[4] Zhu S, Chen Q, Wang X, et al. Dynamic modelling using screw theory and nonlinear sliding mode control of serial robot[J]. International Journal of Robotics and Automation, 2016, 31(1): 63-75.

[5] 赵京,宋春雨,杜滨.基于人体工程学的仿人机械臂构型[J].机械工程学报,2013,49(11):16-21.

[6] 刘迎春,余跃庆,姜春福.机器人可操作性研究进展[J].机械设计与研究,2003,19(4):34-37,7.

Forward Kinematics and Maneuverability Analysis of Humanoid Arm Based on Screw Theory

Li Wenwei1Zhou Guangbing1,2Chen Zaili1Wu Liangsheng1Huang Weicong1Chen Huigang1

(1.South China Robotics Innovation Research Institute 2.Guangdong Institute of Intelligent Manufacturing)

In order to analyze the motion performance of the humanoid arm, the forward kinematics and maneuverability analysis of the SRU humanoid arm were carried out by means of screw theory. Firstly, the forward kinematics of the arm was analyzed based on the product of exponential formula, and the general analytical formula of the forward kinematics solution was obtained. Secondly, the Jacobian matrix of the arm was calculated based on the motion screws, and the global relative maneuverability of any point in the operating space was derived by the Jacobian matrix. Finally, the forward kinematics and maneuverability of a humanoid arm with six degrees of freedom were analyzed, and the visualization results were given.

Humanoid Arm; Screw Theory; Forward Kinematics; Product of Exponential; Jacobian Matrix

李文威，男，1981年生，博士，助理研究员，主要研究方向：智能机器人、CAE仿真与优化、机械动力学。E-mail: liwenwei011@163.com

周广兵，男，1984年生，硕士，工程师，主要研究方向：智能服务机器人、智能制造装备。

陈再励，男，1989年生，硕士，工程师，主要研究方向：机器人智能控制、无人机飞行控制。

吴亮生，男，1988年生，本科，助理研究员，主要研究方向：图像处理、数据通讯。

黄炜聪，男，1988年生，硕士，工程师，主要研究方向：管理信息系统开发。

陈惠纲，男，1984年生，本科，工程师，主要研究方向：仪器、仪表开发。

2018年佛山市军民融合及可持续发展科技项目（2018AG100143）