一种改进的应用于多模式串匹配的KR算法
2018-03-02董志鑫李馨梅
董志鑫, 李馨梅
(1 哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001; 2 对外经济贸易大学 保险学院, 北京 100029)
引言
KR算法[1]是一种直观的基于某个散列函数的模式匹配算法,KR算法首先对模式串和文本中相同长度的子串按哈希函数[2]求值,如果哈希值相同,则逐一比较模式串和子串。一个良好的哈希函数,不同子串的哈希值相同的概率很小,且匹配速度快。KR算法理论上最坏情况下的时间复杂度是O(m×n),但实际应用中平均时间复杂度是O(m+n)[3]。KR算法属于暴力算法[4]的改进型。KR算法设计的最初思想是考虑到每一次模式串在与目标串进行匹配时需要比较每一个字符,效率很低。而KR算法在每次比较时,使用哈希函数,分别计算出模式串以及目标文本段的hash映射,通过比较映射哈希值是否相等来确定字符串。但是因为存在hash冲突的可能性,所以在哈希值相同时还需进一步比较字符串是否相同。在每次比较时需计算哈希值,所以选择合适的哈希算法将尤为重要。
1 常见的哈希函数分析
哈希函数具有很多的用途,其中心思想是把一个大对象映射到另一个比较小的对象,可节省空间,以便于数据保存;或者进行转换,来加密原来的对象;或者在对字符串等数据研究处理后,便于查找、比较等功能实现。本文主要利用哈希函数应用于字符串,来进行字符串的比较[5]。
1.1 哈希函数分类
研究可知,哈希函数可以分为4类,现给出阐释解析如下。
(1)加法哈希函数[6]。就是把字符串中所有元素均加起来,这种方法不用考虑字符串中每个字符的顺序,比较适合本文算法的要求。一般加法哈希函数的构造如下:
intadditiveHash(stringkey, intprime)
{
inthash,i;
for (hash=key.length(),i= 0;i hash+=key.charAt(i); return (hash%prime); } 其中,prime为一个比较大的素数,保证每个字符串的哈希值不会很大。 (2)位运算哈希函数[6]。就是利用移位或者异或等各种位运算来处理输入的字符串,此种方法在计算整个字符串的哈希值时,都要对前期运算得到的哈希值进行位运算,这是基于字符串中字符的顺序来定制设计了,字符相同但位置顺序不同的字符串经过位运算后得到的哈希值不同,不适用于本文中的算法。一般位运算哈希函数的构造如下: static introtatingHash(stringkey, intprime) { inthash,i; for (hash=key.length(),i= 0;i hash= (hash<<4)^(hash>>28)^key.charAt(i); return (hash%prime); } (3)乘除法哈希函数[7]。就是对字符串中的字符进行乘除运算,由此得到字符串的哈希值。一般乘法哈希函数的构造如下: static introtatingHash(stringkey, intprime) { inthash,i; for (hash=key.length(),i= 0;i hash=hash*33 +key.charAt(i); return (hash%prime); } (4)混合哈希函数[8]。就是综合利用上述方式进行哈希运算,得到字符串的哈希值。 KR算法一般所使用的哈希函数算法为加法和乘法混合使用的算法,可以表示为: Hash(x[0,1,2,…,m-1])=(x[0]*2^(m-1)+x[1]*2^(m-2)+…+x[m-1]*2^0) 对于模式串其哈希值是不变的,而目标串每移动一个字符需重新计算,即: Hash(x[i+1,i+2,…,i+m])=(Hash(x[i,i+1,…,i+m-1]) -x[i] * 2^(m-1)) *2+x[i+m] 很明显,该算法考虑了字符串中每个字符的顺序,字符相同、顺序不同的哈希值则不同,这与本文对KR算法改进的思想不同,本文需要寻找一个不考虑字符顺序的哈希函数设计方法。 综合分析了上述多种哈希算法,针对本文需求设计提出了如下的哈希函数算法。本算法的根本思想是利用加法哈希函数,首先设计一个等比数列,公比和首项的选取根据模式串的规模和其中包含的不同字符数目来决定,模式串集合中每个字符对应等比数列中的一项,在计算整个模式串的哈希值时,直接将对应字符的哈希值相加得出的结果作为整个模式串的哈希值。设等比数列为arr[n],则: 选取等比数列中的值作为模式串中每个字符的哈希值,是因为在相同项数的情况下,等比数列的各项相加和不可能相等。本文借助计算机用暴力枚举的方法进行逐一列举,并未发现哈希值相同的情况。 本文提出一种基于上述哈希算法的DKR算法,并运用到多模式串匹配上。研究中,该算法能够准确地匹配到模式串,对比实验显示了该算法的有效性。 2.1.1 预处理中的值设定 首先对于模式串中出现的字符,选取包含整个模式串集所有字符的最大集合M,必须能涵盖所有模式串中出现的所有字符,通常可选取ASCII码集,记为集合H。对于互联网上网址型数据,URL只能使用英文字母、阿拉伯数字和某些标点符号,不能使用其他文字和符号。这是因为网络标准RFC 1738[9]做出了硬性规定:只有字母和数字[0-9a-zA-Z]、一些特殊符号“$ - _ . + ! * ’ ( ) ,”[不包括双引号]、以及某些保留字,才可以不经过编码直接用于URL。 对集合H中的每个字符赋值,该值直接关系到哈希函数的好坏,本文选取字符对应的ASCII码值减去某固定值b,得到的值取另一个定值x(x>1)的次幂。减去固定值b是因为ASCII码表所对应的某些字符一般不出现在模式串集合中,使得模式串字符集M中字符对应的哈希值都比较小,避免出现较大数的情况。针对不同的模式串集合,值b可以变化。本文在处理数据时,采用了ASCII码集作为模式串的字符集合,因为ASCII码表中,用十进制数表示字符,则0~31及127(共33个)是控制字符或通信专用字符,这些不出现在模式串中,而且32代表的空格,也不会出现在模式串中,所以在ASCII码表中,模式串中代表数字最小的字符为叹号(!),其所代表的数字为33,因此在本文的实验测试中,固定值b取33。 对于x的取值,不仅关系到每个字符对应哈希值大小,而且还涉及到运算是否简便。x取2时进行幂运算的花费时间较少,但是会造成部分字符对应的哈希值太大。此时应该调取mod(k)函数,k为一个较大的素数,保证在字符集M中的每个字符都可得到一个合理且不相同的哈希值,并尽量保证不同字符的哈希值相加结果不同。 这里,基于上一节中设计的哈希函数,研究将选取等比数列,计算出字符集M中的字符个数m,确定等比数列公比q,生成首项为1,公比为q的等比数列,并选取前m项,由此构成的集合S作为模式串字符集M对应的哈希值集合。根据上述分析可知,集合S中任意相同数量的项相加和均不相同,所以对于每个字符所对应等比数列中具体哪一项,不用考虑顺序。而且,还可依据目标文本发生动态改变。对于目标文本中出现次数较多的字符可以选用等比数列中位置排前的项,对应的哈希值较小,有利于计算机的求值,可进一步减少运算时间;对于出现较少的字符选用等比数列中相对偏后的项,字符对应的哈希值较大。 2.1.2 求得基准长度PLBase 研究中,求出模式串集合P中最短和最长模式串的长度,分别记为PLmin和PLmax;若PLmax-PLmin<10(该值表示最短模式串长度和最长模式串长度相差不大),对模式串集合P中的模式串长度大于PLmin的取前PLmin个字符,若前PLmin个字符与之前某个模式串的前PLmin个字符相同或者字符对应的哈希值不计顺序相加结果值相同,则从该模式串的第二个字符开始选取PLmin个字符;若仍与之前某个模式串的前PLmin个字符相同或者字符哈希值之和相同,则从该模式串的第三个字符开始选取PLmin个字符,依此类推,直到选取出模式串PLmin长度的代表段所对应的哈希值均不相同。 对于最短模式串长度和最长模式串长度相差比较大的情况,研究采取另一种方法,对其展开论述如下。 对每个模式串的长度进行统计,选取出现频率最高的模式串长度记为PLbase。把小于PLbase长度的模式串与大于等于PLbase长度的模式串分类,各自存储起来,而且并行地开启模式串匹配识别流程。对于小于PLbase长度的字符串,按照上述方法,选取这些模式串中的最短长度,记为PLmin,继续按照上述方法进行处理,得到每个模式串的哈希值。对于不小于PLbase长度的模式串,以PLbase为基准,选取前PLbase个字符,若前PLbase个字符与之前某个模式串的前PLbase个字符相同或者字符所对应的哈希值不计顺序相加结果值相同,则从该模式串的第二个字符开始选取PLbase个字符;若仍与之前某个模式串的前PLbase个字符相同或者字符哈希值之和相同,则从该模式串的第三个字符开始选取PLbase个字符,依此类推,直到选取出模式串PLbase长度的代表段所对应的哈希值均不相同,此时选出的PLbase个字符串段代表原模式串段。在匹配时,首先匹配代表段,若代表段相同,再匹配代表段所对应的原模式串,两次匹配成功才能完成匹配。 不失规范性,将上述2种方法中的PLmin和PLbase统称为PLbase。方法不变,则将利于后续文章的书写。同时为了方便上述的处理,对模式串进行存储时,增加存储模式串的长度,并在新增、修改模式串时,一并新增或更改模式串长度的数值,这样在预处理时就可对模式串的长度做出整合统计,选取出现次数最多的模式串长度,以及最长、最短的长度,不仅实效便捷,而且不会增加太多存储空间。 2.1.3 哈希值的研究设定 经过上述处理后,按照集合M中字符对应的哈希数值,对每个模式串中包含的字符对应数值不计顺序相加,得到每个模式串对应的哈希值,尽可能地实现每个模式串对应的哈希值唯一。若不唯一,可采取3种方法进行处理使哈希值唯一,执行方法具体如下: (1)对字符集合M重复赋值,在上述赋值的基础上每个值再乘以(或除以)一个相同的素数,或者对每一个值都乘以一个不同的素数。 (2)调整变换字符集M所对应的等比数列集合S,进行更改,更改等比数列的公比q,在(1,2)之间进行取值。 (3)对具有相同哈希值的模式串,若这些模式串的长度大于基准长度PLbase,按照上述选取方法,继续后移一位选取PLbase长度的标志字符段,直到各个模式串的哈希值不同。 若经过前述3种方法仍然无法避免每个模式串的哈希值不同,那就先按相同来检控处理,当与目标文本匹配成功时,再多比较一步,看具体与哪个模式串相同,但此种情况的概率较低,在本文实验中还并未出现。 最终,模式串集合P有一个对应的哈希值表PH。然后求出每个模式串前半段和后半段对应的哈希值hash_half_before和hash_half_after,仍然保存在表PH中。当模式串长度为奇数时,即PLbase是奇数时,在选择半段(前后半段的统称)长度时,取PLbase/2整数部分加1;当PLbase为偶数时,直接取PLbase/2。这种做法就使得与目标串段匹配时,只考虑包含大于等于模式串50%的部分,保证算法的有效性。 接下来,将继续求出包含该模式串前半段或者后半段的具有PLbase长度的最小哈希值MinH,即选取包含前半段的最小值和包含后半段的最小值中的最小的那个记为MinH。设该半段的长度为L_half,对于PLbase-L_half部分用字符集H中具有最小哈希值的字符来补充,这样补全的长度为PLbase的字符串的哈希值即为MinH,该哈希值一定是包含该半段模式串的任何字符串中具有的最小哈希值,因为如果别的字符串包含该半段,则其余部分肯定具有大于最小哈希值的字符,那最终的哈希值肯定不是最小哈希值MinH。这样保证在匹配时,只要该目标段的哈希值比最小哈希值MinH小,则该目标段就必然不能与该模式串匹配,将该模式串记为无效,在对该目标段进行的后续匹配中,无需比较无效的模式串。而后将hash_half_before,hash_half_after,MinH三个值均保存在表PH中。如果用结构体表示模式串的每个属性,则该结构体如下: struct _pattern_data { unsigned chardata[MAX_PATTERN_LEN]; //模式串 unsigned chardata[MAX_PATTERN_LEN]; //模式串代表段 intlen; //模式串长度 doublehash; //模式串哈希值 doublehash_half_min; //包含模式串半段的最小哈希值 doublehash_half_befor; //模式串前半段的哈希值 doublehash_half_after; //模式串的后半段的哈希值 intflag_is_useful; //模式串在当前匹配时,是否有效 } pattern_data ; 首先利用上述算法计算出每个模式串的哈希值,再利用上述数据结构来存储每个模式串的信息,对模式串施以统一的预处理后,将相关信息进行存储,以备后续使用。 引理1对于长度为m的字符串Str,将其分成2个字符串Str1和Str2,则Str1或者Str2至少有一个其中包含不少于50%的Str中的字符个数。该引理可用反证法证明。 证明假设Str1和Str2没有一个包含不少于50%的Str的字符个数。 设Str1包含a%的字符个数,Str2包含b%的字符个数(a% < 50%,b% < 50%)。 则a%+b% < 100%,这与字符串Str分成两个字符串Str1和Str2矛盾。 所以,该理论为真。 根据引理1可知,任何一个模式串只要被包含在目标串中,目标串的PLbase划分中一定有一个分段包含该模式串至少50%的字符,运用该引理,对目标串T进行PLbase划分,对于每个划分设立一个变量p,表示该划分包含模式串的概率。然后根据2.1节中字符集M中字符对应的哈希数值表,对每个划分求取哈希值B。将哈希值B与模式串的哈希值A进行比较,分析处理过程如下: (1)若与某个值A相等,则将该划分的概率p设为100%,并将该划分与哈希值为A的模式串进行比较,若2个字符串相等,则进一步验视该模式串是否为模式串的代表段。若是代表段,则还要续接与原模式串的设计匹配,因为原模式串长度肯定比划分的长度(PLbase)大,此时应在该划分后面继续比较,一直比较到某个字符与原模式串不同,或者匹配到原模式串长度后,则表示匹配成功,继续下一划分的匹配。 (2)否则,与表PH中的最小哈希值hash_half_min进行比较,若小于该表中的某个模式串的最小哈希值,则将该划分在当前匹配中的有效性flag_is_useful置为无效,表示该划分不包含该模式串不小于50%部分,后续无需对该划分处理时考虑该模式串。 (3)对该划分从第一个字符开始计算前PLbase/2个字符的哈希值,将此哈希值与模式串前后半段的哈希值(hash_half_befor和hash_half_after)进行比较,若与某个模式串前半段的哈希值相等,则将该划分的PLbase/2个字符与这些字符后的PLbase/2个字符进行相连,然后与该模式串进行比较,若相等则匹配成功,否则匹配失败,从下一字符开始继续计算PLbase/2个字符的哈希值,继续按照上述方法进行比较,直至该划分的第PLbase/2个字符时比较终止,停止该划分比较,继续下一划分的匹配。举例说明如下。 假设目标串T为12345abcdefghij67890,划分段Tk为abcdefghij,详细过程可阐释为: (1)首先计算Tk的哈希值Hash(Tk),与每个模式串的哈希值比较,若与模式串Px相同,则分析Px是否为原模式串。若为原模式串,则判断Tk与Px是否相同,得出匹配结果;若Px不是原模式串,则将原模式串与目标串划分段及其后续字符(67890部分)进行比较,比较时保证2个字符串长度相同。 (2)若Tk的哈希值Hash(Tk)小于模式串Py的最小哈希值,则将该模式串的有效位置为无效。 (3)选取Tk的前PLbase/2个字符abcde,计算这5个字符的哈希值H_temp,将H_temp与每个模式串前后半段的哈希值(hash_half_befor和hash_half_after)进行比较,若与某个模式串Pz的前半段相等,则将字符a的前面的PLbase/2个字符12345,与字符abcde相连,构成字符串12345abcde,与模式串Pz进行比较,若相同,匹配成功,继续下一划分匹配;若与某个模式串Pz的后半段相等,则将最后一个字符e后续的PLbase/2个字符fghij,与字符abcde相连,构成字符串abcdefghij,与模式串Pz进行比较,若相同,匹配成功,继续下一划分匹配。否则,继续从第二个字符b开始,选取PLbase/2个字符bcdef这5个字符,计算相应的哈希值,进行同样的比较,一直到目标串结束。 因为根据引理1,若目标串存在模式串,必然有一个划分包含大于等于50%的模式串,因此只需考虑每次单元划分的50%,在这个划分的50%里没有查到,就不可能存在该划分中,因而将继续在下一个划分中查找,则无需查找该划分中全部的字符。 按照上述方法从目标串第一划分开始处理,一直到最后一个划分,若最后一个划分小于PLbase长度,则直接可以不用比较。原因在于此时模式串的长度都大于该划分,故而不再存在匹配的情况。 本文提出的针对多模式串的匹配算法,与AC自动机算法[10]相比,首先在空间复杂度上就具有显著优势。本算法的空间复杂度为O(n),而AC自动机算法的空间复杂度则为指数级的。并且无论将如何优化,AC自动机算法都很难达到本算法的空间复杂度。 在时间复杂度方面,本算法也具有突出优势,主要探讨解析如下。 2.3.1 预处理上的时间复杂度分析 本文研究中主要是对模式串进行预处理,设模式串个数为m,模式串的平均长度为基准长度,即PLbase。过程中涉及指定的操作主要有统计模式串中所有出现的字符,构成字符集M,时间复杂度为O(m*PLbase);统计每个模式串的长度,时间复杂度为O(m);选取出现最多的长度PLbase,时间复杂度为O(m);计算每个模式串的哈希值、模式串前后半段的哈希值、模式串对应的最小哈希值,这3项操作的时间复杂度均为O(m*PLbase),所以预处理最终的时间复杂度为O(m*PLbase)。 2.3.2 匹配过程的时间复杂度分析 对于每一个文本段,本算法在实际的运用中都会有多个模式串无需送入验证比较。因为在对每一段目标串进行处理时,首先计算该目标串段的哈希值,如果该目标串段的哈希值比某个模式串所对应的最小哈希值还小,则该模式串对于本目标段不会匹配成功,属于无效模式串,在处理本目标串段时可以忽略该模式串。 假设每次无需比较的模式串为h个,目标串长度为n,模式串的基准长度为p,则完成一次匹配,可优化减少的匹配次数为hn/p次。相对于每个字符均需比较的情况,本算法可以减少的比较次数占总比较次数比值为h/p。在实际的测试中该比值并不小,在本次研究测试中,该比值平均为24.49%。 在比较的过程中,每次以模式串基准长度PLbase为标准长度,即目标文本段的长度,对各段每次需要比较PLbase次,获得目标文本段加上前后目标文本段的后半段和后个目标文本段的前半段之后的总文本段,对其计算哈希值,也就是计算PLbase个长度为PLbase的目标文本段的哈希值,经过与上述第一步后仍然有效的模式串哈希值进行比较,比较结束后每次跳跃PLbase个长度。相较于AC自动机算法,本算法每次跳跃的距离很大,因为在处理目标串时的方法原理不同,不能只是简单地比较跳跃距离,还应计算一个长度为n的目标串,2个算法将调用展开的比较次数。设模式串个数为m个,模式串平均长度为L,目标串长度为n,研究可得分析过程如下。 2.3.2.1 最坏情况下比较 AC自动机算法的最坏情况下比较次数C为: C=m*n*L (1) DKR算法的最坏情况下比较次数C为: C=m*n/L (2) 如果再加上求取哈希值所使用的加法运算,把加法运算与比较运算都算作一次运算的情况下(因为在汇编语言指令下都是一个操作,而且实质上比较大小是做减法),DKR算法的最坏情况下比较次数C为: C= (L*L/4+2m) *n/ 2L (3) 基于前文探讨结果,对其给出说明如下。在加法运算与比较运算都算作一次运算的前提下,此时将PLbase基准模式串长度看作模式串平均长度L,则目标串总共可分为n/L段,对于每一目标段只需计算该段的前半段哈希值。因为根据引理1的结论,模式串若存在目标段中,对于任意目标段肯定有一段是包含不少于一半模式串,研究只考虑半段即可。对于每一段目标串,都要计算L/2个字符相加得到哈希值,对于该半段中以每个字符开头的PLbase/2长度的段,都要计算哈希值,统共要计算L/2次。所以,加法运算的运算次数为L*L/ 4。计算出哈希值后,需要与模式串的前后半段的哈希值设定比较,对于m个模式串每段就需要比较2*m次。 从上述3个公式可以发现,在不考虑加法运算的情况下,只要L>1,公式(1)中比较次数C就大于公式(2)中的比较次数。考虑加法运算后,只需要在L*L> 8*m/ (8*m-1)时,公式(3)中的比较次数C就小于公式(1)的比较次数,即DKR算法的比较次数小于AC自动机算法的比较次数。因为在运行实践中,无论m多大,L*L都会远大于8*m/ (8*m-1)。所以,在最坏情况下,DKR算法的比较次数明显小于AC自动机算法,即DKR算法的时间复杂度明显优胜于AC自动机算法。 2.3.2.2 一般情况下比较 AC自动机算法在匹配过程中存在可跳跃的情形,从而达到减少比较次数的目的。跳跃的情况,则根据不同的模式串有不同的情况。在最优的情况下,时间复杂度可以达到O((m+n)L)。 DKR算法在匹配过程中对每段不同的目标文本段,都包含不用比较的模式串个数,而当目标串与文本串差别较大时,算法效率则将提升。理想情况,每次只剩下一个模式串,即命中模式串,无需与别的模式串比较。至于匹配成功的目标串的前半段比较就相等,即2*m= 1,此时算法效率极高,时间复杂度为O((L/8+1 /8*L)*n),约为O(n*L/8)。 存在直接找到的情况也并不少见,即目标串划分的哈希值与模式串哈希值相同,但却非一定是匹配成功,需要再次验证一次即可,而且可能存在顺序不同,因为本哈希函数不考虑顺序问题。最高出现次数的模式串长度PLbase,所以不论什么样的文本都有很高的几率,即使只有1%的机会直接命中,对于分类型数据的效率提升也相当高。 本算法自动包含坏字符规则,对于并未在字符集中出现的字符,则没有相关的哈希值与该字符对应,可直接跳过,将匹配串直接移动到该字符下一字符进行匹配。 在实际应用中,比如一些网络监测系统,模式串是有一定的规则和格式的,那么子串重复的可能性就会减少。因此,使用哈希函数h(X) 计算字符串的值,通过比较函数值来代替逐一的字符串比较可以减去至少(l-lm) 的无用子串比较。 本算法在预处理上,主要存储模式串的4个哈希值表,其空间复杂度为O(m)。而AC算法,因为存在Trie树的存储和失败指针的存储导致可观空间消耗,不管采用怎样的存储优化,其空间消耗也都是指数级的,由此带来的空间复杂度均为指数级。因此算法在空间复杂度上的优势相当明显,在模式串数量较多的情况下,本算法将呈现巨大优势。 为了对上述算法提供合理全面的性能验证,本节将DKR算法和AC算法在同样的实验环境下,对同样的模式串和目标串进行验证,验证的主要标准是比较各自的时间效率和空间占用情况,然后通过对结果的分析得出最终结论。 操作系统:Ubuntu 16.04(64位); 处理器:Intel(R)Core(TM) i7-2670QM CPU @ 2.20 GHz ; 处理器核心数:4核; 编译器:gcc version 5.4.0; 编程语言:c语言。 因本文主要研究算法的高效性,而且是在线匹配的高效,所以只对2种算法的匹配时间效率进行分析,暂不考虑算法的空间效率(占用内存大小)和算法的预处理时间。 实验选用的数据中,测试目标文本大小为100 M;模式串集个数分别为1 000,5 000,10 000,模式串长度则为5~1 000内,任意长度。 算法运行预处理时间可见表1。 表1 不同模式串个数对应算法预处理时间Tab. 1 Preprocessing time of string matching in different patterns 算法运行匹配时间可见表2。 表2 不同模式串个数对应算法匹配时间Tab. 2 Matching time of string matching in different patterns 算法采用的是Linux中/usr/bin/time命令,内存的占用选取的是最大驻留集的大小来表示程序运行中内存占用的最大量。 算法运行内存最大占用量可见表3。 表3不同模式串个数对应算法内存最大占用量 Tab.3Maximummemoryusageofstringmatchingindifferentpatterns 模式个数/个DKR算法/KBAC算法/KB1000102376138892500011059229078810000120876478124 通过对以上结果的分析,本文所提出的DKR算法在多模式串匹配的预处理和内存占用上具有显著鲜明优势。而且随着模式串个数的增多,本算法实际展现出来的优势就越发明显。但是本算法在匹配时间上效率并不如AC算法,这在此后的实验中,将进一步展开研究优化,以达到更好的效果。 本文首先论述了KR算法,分析了常见的哈希函数,根据DKR算法的思想提出了相应的哈希函数算法,同时详细研究了该算法对模式串的预处理过程以及算法的匹配过程,并将该算法与AC算法在时间复杂度和空间复杂度两个方面进行了阐释分析。实验结果显示,该算法在多模式串匹配的预处理和内存占用上具有相当大的优势,证明了算法的有效性。 [1] KARP R M, RABIN M O. Efficient randomized pattern-matching algorithms[J]. IBM Journal of Research and Development—Mathematics and computing,1987,31(2):249-260. [2] “科普中国”百科科学词条编写与应用工作项目. 哈希函数[EB/OL].[2017-06].http://baike.baidu.com/link?url=_mdPrKjxu9EOMuUgQ18D55OO9Mti5FJ1pE7Ov_3gO9Ccs7fGarPGN_VVWCOboUm33y1AX6lksC6iLsl8VezzbDXxLgPIN17luuKQ-IPc B1tkHjvqFVyIkLu_vQGBIv0T. [3] KNUTH D E,MORRIS J H,PRATT V R.Fast pattern matching in strings[J]. SIAM J Computing,1977,6(2):323-350. [4] 毛先森. 字符串匹配—暴力匹配算法[EB/OL]. [2016-08-12]. http://www.cnblogs.com/Kevin-mao/p/5764726.html. [5] 叶军伟. 哈希函数构造方法及其适用情况[J]. 科技致富向导,2014(8) :278. [6] HORSPOOL R N. Practical fast searching in strings [J]. Software Practice and Experience,1980,10(6):501-506. [7] WU Sun, MANBER U. A fast algorithm for multi-pattern searching[R]. Tucson:University of Arizona, 1994. [8] Chinaunix.几种常用hash算法及原理[EB/OL].[2016-08-09]. http://blog.chinaunix.net/uid-30592332-id-5749402.html. [9] Network Working Group. RFC 1738 - Uniform Resource Locators[EB/OL].[1994-11]. https://tools.ietf.org/html/rfc1738.html. [10]AHO A V, CORASICK M J. Efficient string matching: An aid to bibliographic search[J]. Communications of the ACM, 1975, 18(6):333-340.1.2 KR算法解析
1.3 本文设计的哈希函数算法
2 DKR算法
2.1 模式串的预处理
2.2 目标串的处理与匹配
2.3 算法分析
3 实 验
3.1 实验环境
3.2 实验结果
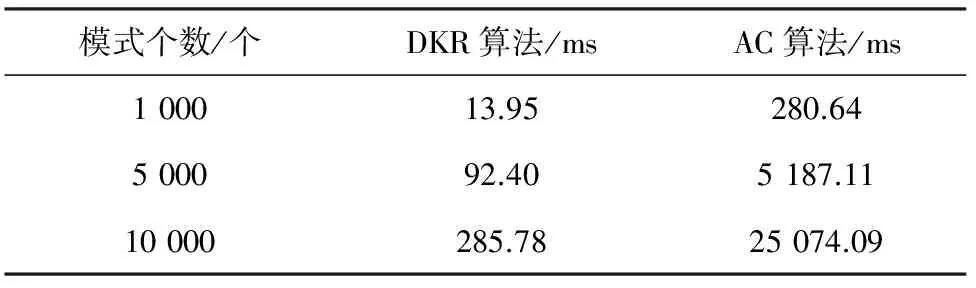
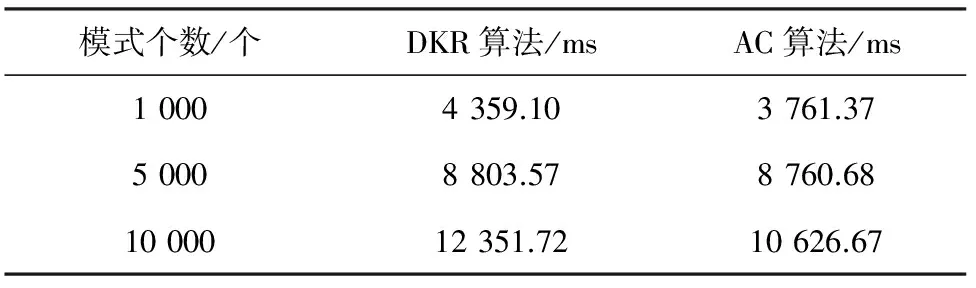
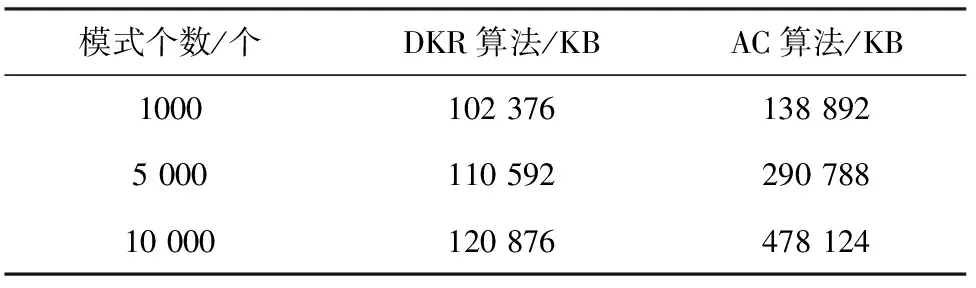
3.3 实验分析
4 结束语
