基于模糊神经网络的油气运输管道调度技术

王 子， 朱朋勇

(中石油管道有限责任公司 西气东输分公司, 杭州 310006)

引言

油气管道是油气运输的重要载体，油气运输管道网络的优化节点部署设计是保障油气运输网络可靠稳定运行的关键，通过对油气运输管道网络的优化路径规划和调度设计，降低管道部署的开销，提高油气运输的吞吐性能。油气运输管道网络具有自组织性，以各个压气站为节点进行全局网络设计，在整个管道组网设计中，受到地理环境、用户分布情况以及压气站分布情况等各种因素的影响，导致油气运输管道运输调度变得复杂，油气运输的管道调度是一项系统性的综合网络工程，需要研究一种优化的油气运输管道调度技术，提高油气运输管道的全局稳定性和畅通性，保障大型油气运输工程的安全稳定运行[1]。

对油气运输管道调度是建立在对管道网络的综合节点定位和路由优化设计基础上的，通过建立管道网络的无线组网结构模型，采用自适应传感器组网设计方法进行路由分发设计，提高管道网络的连通性和覆盖能力，传统方法中，对油气运输管道组网和调度方法主要有最大角度路由选择算法、不规则三角网组网调度方法、最少跳数路由调度方法等[2-3]，通过优化的路由算法设计，最大化油气运输管道的覆盖范围和吞吐量，提高管道油气运输能力，取得了一定的研究成果。其中，文献[4]中提出一种剩余能量均衡调度的油气运输管道的组网调度模型，采用动态自适应性路由节点定位技术进行管道节点的组网设计，设计均衡控制方法提高油气运输管道网络传输的均衡性，但该组网控制方法抗局部干扰能力不强，全局均衡性不好；文献[5]提出一种基于量化传感融合跟踪识别的油气运输调度技术，采用无线传感组网技术进行管道节点的优化部署设计，结合量化分析方法提高管道节点对油气的自组织收发能力，整个网络的畅通性较好，但该组网结构复杂，在应对大规模的油气运输管道调度时的工程实践应用性不好。

针对上述问题，本文提出一种基于变结构模糊神经网络控制的油气运输管道调度技术。首先采用三层变结构的PID神经网络模型进行油气运输管道的网络结构模型，然后采用地理位置寻优算法进行油气运输管道组网的最优路由设计，以各个压气站为Sink节点进行能量融合均衡调度，建立油气运输管道调度的控制目标函数并进行全局稳定性求证，根据模糊神经网络的积分控制方法进行管道调度的路径规划最优解求解，缩短了管道组网路径，提高管道网络的吞吐性能和均衡性。最后进行仿真测试，得出有效性结论。

1 油气运输管道的网络结构模型

1.1 三层变结构的PID神经网络

为了实现对油气运输管道调度优化，首先进行网络组网结构模型分析，采用三层变结构的PID神经网络模型进行油气运输管道的网络结构模型研究[6]，如图1所示。

图1 油气运输管道三层变结构的PID神经网络

Fig.1ThreelayervariablestructurePIDneuralnetworkforoilandgaspipeline

在图1所示的油气运输管道组网PID网络结构模型中，输入层有2n个相同的神经元，作为网络的Source与Sink节点，神经元的输入为油气运输管道的当前负载:

(1)

油气运输管道网络过载边的神经元状态为：

usi(k)=netsi(k)

(2)

式(2)表示油气运输管道网络过载边，输入层神经元的输出为：

(3)

表示每个转运节点的能量消耗和路径损耗，为了使得整个网络的路径消耗最小，选定任意一个结点作为开始结点进行均匀遍历，给定能量阈值，令管道运输的失效过载比可表述为：

(4)

当不考虑整个油气运输管道调度系统的不确定因素时，通过2×(m0-1)条有向边连接每个压气站节点，得到管道网络的拓扑控制函数描述为：

(5)

在上述构造的三层变结构的PID神经网络模型中，采用地理位置寻优算法进行油气运输管道组网的最优路由设计，实现管道优化调度。

1.2 地理位置寻优算法

地理位置寻优算法的原理是将运输管道的遍历过程看作一个时间离散的马尔科夫过程[7]，在不同管道铺设路段中，以管道的流量和阻抗状态为约束参量，构造管道调度的滑模面，定义为：

s=ce1+e2

(6)

则根据流量模型可以确定管道网络有向边的分布特征函数：

(7)

令:

(8)

则得到油气运输管道调度的阻抗模型为：

(9)

从已生成的网络中选择终端结点，各支路输出量x1，x2，…，xn分别乘上权重值w1j，w2j，…，wnj，得到油气运输管道调度的等效控制律为：

(10)

考虑系统存在不确定因素，在任意时刻t，对模糊神经网络的第j个神经元进行自学习优选控制，选择到达律为：

(11)

遍历管道网络的结点列表，得到油气运输网络的路由分配函数为：

(12)

对上式进行Lyapunove泛函，实现油气运输网络铺设组网的地理位置自适应寻优，有效降低组网的路径开销。

2 油气运输管道调度模型优化

2.1 能量融合均衡调度

在上述构建了油气运输管道的网络结构模型的基础上，进行油气运输管道调度算法优化设计，本文提出一种基于变结构模糊神经网络控制的油气运输管道调度技术，以各个压气站为Sink节点进行能量融合均衡调度[8]，给出第r轮，节点ni的最优接收油气流量的输出函数由f(·)决定，以神经元状态uj为自变量，得到管道的输出流量状态函数为：

xj(k)=f(uj(t))

(13)

这里采用Sigmoid函数作为能量融合的传导模型，其表达式为：

(14)

采用模糊神经网络控制方法进行管道节点输出流量的自适应调节，对于神经网络的2个Sink神经元，在任意采样时刻k，其输入的油气吞吐量为：

neti(k)=ri(k)i=1,2

(15)

在最优调度策略下，输入层神经元的油气流量控制状态函数为：

(16)

(17)

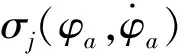
(18)

2.2 油气运输管道调度全局稳定性分析

下面对所设计的油气运输管道调度模型的稳定性进行证明分析。

(19)

假设2在全局综合调度过程中，油气运输量和路径损耗存在不确定控制约束变量的上界满足：

(20)

(21)

(22)

定义Lyapunov函数为：

(23)

(24)

基于Lyapunove稳定性原理，得到本文设计的基于模糊神经网络的油气运输管道调度模型是全局渐进稳定的，系统的稳定性得证。

3 仿真实验与性能测试

为了验证本文设计算法在实现油气运输管道优化调度中的应用性能，进行仿真实验，实验采用Matlab仿真软件设计，实验以1 000 m×1 000 m二维平面作为油气运输管道网络的覆盖区域，管道的Sink节点数量为100，Source节点数量为12，管道网络区域分割的网格大小为24 m2，簇头分布节点数目分别为15,30,30,50,100，在管道中的油气传输速率记为10 Mbps，路由跳数间歇时间为0.2 s，簇首节点的最大覆盖距离为50 m，神经网络的级数为24，神经元个数为100，信道衰减常数为12，传输能量损失为3.249 77 KJ，根据上述仿真环境和参量设定，进行油气运输管道调度仿真，在不同流场下测试不同的调度模型进行油气运输管道调度的均衡性，得到结果如图2所示。

(b)石油流场(b) Oil flow field

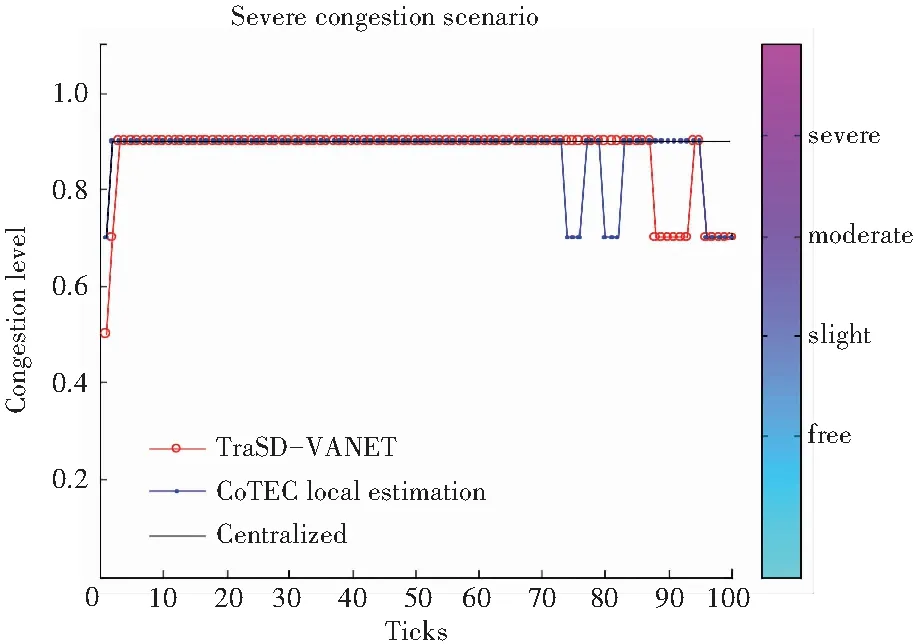
(c)混合流场(c) Mixed flow field图2 不同流场下不同模型进行调度均衡性对比

Fig.2Comparisonofschedulingequilibriaofdifferentmodelsunderdifferentflowfields

分析图2结果得知，采用本文模型进行油气运输管道调度的均衡性较好，输出流量分布曲线的平滑性较好，说明管道输出的全局稳定性较好，最后统计分析得知，本文方法提出的油气运输管道调度的吞吐量比传统方法提高了25.87%，管道铺设路径节省12.65%，效能改善显著。

4 结束语

本文研究一种优化的油气运输管道调度技术，提高油气运输管道的全局稳定性和畅通性，提出一种基于变结构模糊神经网络控制的油气运输管道调度技术。采用三层变结构的PID神经网络模型进行油气运输管道的网络结构建模，采用地理位置寻优算法进行油气运输管道组网的最优路由设计，进行管道运输的能量融合均衡调度，并对调度模型进行全局稳定性分析，研究表明，采用本文模型进行油气运输管道调度的均衡性较好，缩短了管道组网路径，提高管道网络的吞吐量和油气运输的平稳性。

[1] 尤冬石,刘亚龙,殷若鹏. 基于定量递归分析的天然气管线输送流量均衡调度方法[J]. 智能计算机与应用,2016,6(4):16-19.

[2] JIANG Yizhang, CHUNG Fulai, WANG Shitong, et al. Collaborative fuzzy clustering from multiple weighted views[J]. IEEE Transactions on Cybernetics, 2015, 45(4): 688-701.

[3] LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Adaptation regularization: A general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076-1089.

[4] PATRICIA N, CAPUTO B. Learning to learn, from transfer learning to domain adaptation: A unifying perspective[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA:IEEE, 2014: 1442-1449.

[5] SUN Leilei, GUO Chonghui. Incremental affinity propagation clustering based on message passing[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(11): 2731-2744.

[6] 李可,米捷. 基于变结构PID的仿生机器人机电控制算法[J]. 河南工程学院学报(自然科学版),2016,28(2):32-37.

[7] 崔永君,张永花. 基于特征尺度均衡的Linux系统双阈值任务调度算法[J]. 计算机科学,2015,42(6):181-184.

[8] 薛明,许德刚. 基于云网格集成调度的防拥堵车辆路径规划算法[J]. 计算机科学,2015, 42 (7):295-299.

[9] 龚聪. 改进神经网络煤矿安全评价模型仿真研究[J]. 计算机仿真,2012,29(1):156-159.

[10]宋明红,俞华锋,陈海燕. 改进量子进化算法在计算机网络路由选择中的应用研究[J]. 科技通报,2014,30(1):170-173.