基于S修正RBUKF的自适应网格交互式多模型算法

张 园，董受全，刘淑波，初俊博

（海军大连舰艇学院，辽宁 大连 116018）

0 引言

机动目标跟踪中，普通的UKF针对状态方程和观测方程均为非线性、噪声为非加性的这种最一般情况。实际应用会遇到仅观测方程为非线性，而状态方程为线性，且噪声为加性的情况，这时普通的UKF算法可简化为 RBUKF（Rao-Blackwellised UKF）算法。本文首先对这种情况的RBUKF算法进行了修正［1-3］。

机动目标跟踪的主要挑战来自于目标运动模式的不确定。机动目标的多模型方法通过使用不止一个模型来应对这种模型的不确定性，发展至今已经历三代［4］。前两代多模型方法模型群组的成员不随时间变化，称为固定结构多模型（FSMM：Fixed Structure Multiple Model）算法。第三代算法模型集可变，称为变结构多模型 （VSMM：Variable Structure Multiple Model）算法［5］。自适应网格（AG：Adaptive Grid）是基于图论的一种变结构多模型算法。本文采用自适应网格交互式多模型（AGIMM）策略，结合上述修正的RBUKF滤波方法，形成基于S修正RBUKF的自适应网格交互式多模型算法（SRBUKF-AGIMM）。

1 系统描述

设系统的状态空间表达式为

式中，xk为n维状态矢量，对于本文使用的CV和CT模型，；zk为m维观测矢量；Φk、Γk分别为状态转移阵和干扰转移阵；wk、vk分别为系统噪声和观测噪声，假设为零均值、互不相关的高斯白噪声，方差阵分别为Qk和Rk；假定雷达在极坐标系观测，则观测矢量与状态矢量间的非线性函数关系。

采用多模型算法时，可假设第j个模型的状态方程为

2 算法步骤

SRBUKF-AGIMM算法步骤如下。

2.1 输入矢量的交互

设模型集中有模型r个，则对于j=1，…，r

2.2S修正的RBUKF

对于模型集中的每个模型j=1，…，r

2.2.1 线性时间更新

2.2.2 选取sigma采样点

2.2.3 非线性量测更新

2.2.4 防发散修正［6］

其中，s为一标量常数，可根据经验选取，一般取s＞1。

返回2.2.2；否则，继续2.2.5。

2.2.5 后续量测更新

两式中，

这里，β=2。

2.2.6 滤波矢量的更新

2.3 模型概率的更新

似然函数：

模型概率更新：

2.4 输出矢量的交互

2.5 模型集自适应网格调整

3 仿真实验

为了验证SRBUKF-AGIMM算法性能，将其与IMM3 和 IMM7 进行比较，这里 IMMn（n=3，7）表示IMM算法中模型集分别由3和7个固定模型组成。滤波算法采用基本UKF算法。

假设目标在x-y平面蛇形机动，仿真中采用的测试轨迹如图1所示，仿真场景如下［9-10］：初始位置为（-1 000 m，-3 000 m），初始速度为 500 m/s（与 x轴的夹角为45°），仿真时间为200 s。仿真轨迹由5段角速度不同的转弯运动组成：目标在0≤t≤75 s内 ω=-0.02 rad/s，在 76 s≤t≤125 s内 ω=0.04 rad/s，在 126 s≤t≤160 s内 ω=-0.06 rad/s，在 161 s≤t≤183 s内角速度为ω=0.08 rad/s，在184 s≤t≤200 s内 ω=-0.10 rad/s。

仿真时，IMM3 使用的模型集为{ω=-6°/s，ω=0°/s，ω=6 °/s}， 模 型 转 移 概 率 均 为 p=［0.7，0.2，0.1；0.2，0.7，0.1；0.1，0.2，0.7］。IMM7 使用的模型集为{ω=-6°/s，ω=-4°/s，ω=-2°/s，ω=0°/s，ω=2°/s，ω=4°/s，ω=6°/s}，模型转移概率为。pii=0.9，i=1，7；pii=0.8，i=2，6；pii-1=0.1，i=2，…，7；pii+1=0.1，i=1，…，6。设量测噪声为零均值、标准差为diag［150 0.3］高斯噪声。

SRBUKF-AGIMM算法中每个时刻的模型集由3个模型组成，模型集中各模型交互概率同IMM3算法。最小网格间隔取为δω=0.5°，重要模型概率门限取为t2=0.92，不可能模型概率门限取为t1=0.05。

取采样周期为T=1 s，分别对各算法进行100次Monte Carlo仿真，IMM3和SRBUKF-AGIMM算法的位置均方根误差（Root Mean Squared Error，RMSE）和速度RMSE的仿真曲线分别如图2～图5所示。SRBUKF-AGIMM、IMM3和 IMM7算 法 的 位 置RMSE和速度RMSE的仿真结果如表1所示，3种算法的平均计算时间如表2所示。

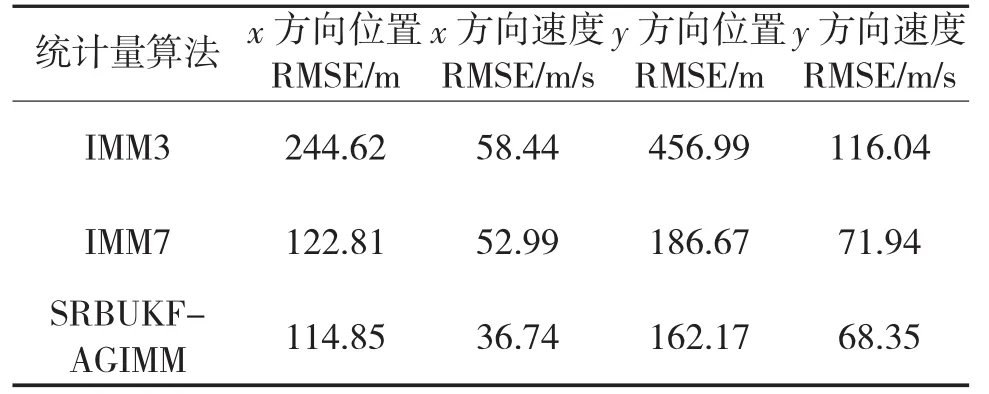
表1 100次蒙特卡罗仿真结果

表2 100次蒙特卡罗仿真平均计算时间

由仿真过程、图2～图5和表1、表2可以看出：

1）本文提出的SRBUKF-AGIMM算法与IMM3算法相比，模型集使用模型个数相同（3个）、计算时间相当，跟踪精度大幅提升（x、y两个方向的位置RMSE分别减小113%和181%，x、y两个方向的速度RMSE分别减小59%和70%）；与IMM7算法相比，跟踪精度有所改善（x、y两个方向的位置RMSE分别减小7%和15%，x、y两个方向的速度RMSE分别减小44%和5%），使用模型个数大幅减少（由7个减为3个），计算时间大幅缩短（由2.21 s减为0.323 s）。因此，可以说，SRBUKF-AGIMM算法与固定结构多模型（FSMM）算法相比，可在计算量相当的情况下大幅提高跟踪精度，或在保持跟踪精度相当的情况下大幅降低计算复杂度和计算时间。总之，可以大幅提高算法的费效比。

2）与模型集模型个数相同的固定结构多模型（IMM3）算法相比，SRBUKF-AGIMM算法在模型集可跟踪范围内，目标的机动性越强，跟踪精度的改善优势越明显。在 0≤t≤75 s、76 s≤t≤125 s目标转弯机动的角速度比较小时，SRBUKF-AGIMM算法的跟踪精度优势不够明显；在126 s≤t≤160 s、161 s≤t≤183 s、184 s≤t≤200 s目标转弯机动的角速度比较大时，跟踪精度有明显改善，并且目标在这3个时间段的角速度依次增加时，跟踪精度改善的幅度依次变大。

3）在仿真过程中，保持前三段的角速度的值不变，增大后两段的角速度的值，使其值分别超出左模型（ω=-6°/s）和右模型（ω=6°/s）。以 x方向为例，设x方向位置RMSE最大容许误差为1 500 m（即当方向位置RMSE超过1 500 m时，则认为算法无法跟踪），对于左转弯运动时，应用IMM3算法时，目标的角速度超过左模型（ω=-6°/s）的 15.7%时，就无法跟踪；而应用SRBUKF-AGIMM算法时，目标的角速度超过初始左模型（ω=-6°/s）303%时，才无法跟踪。目标右转弯运动时结果与此类似。这充分显示了变结构多模型在目标机动超出模型集覆盖范围时强大的自适应能力，因此，SRBUKF-AGIMM算法能够弥补固定结构多模型算法在这方面的先天劣势。

4 结论

本文研究了一种S修正Rao-Blackwellised UKF和自适应网格的机动目标跟踪变结构交互多模型算法。该算法与固定结构多模型（FSMM）算法相比，可在计算量相当的情况下大幅提高跟踪精度，大幅提高算法的费效比。并且在模型集可跟踪范围内，目标的机动性越强，跟踪精度的改善优势越明显。另外，该算法在目标机动超出模型集覆盖范围时表现出强大的自适应能力。

［1］刘江，陆明泉，王忠勇.RBUKF算法在GPS实时定位解算中的应用［J］. 系统工程与电子技术，2009，31（11）：2578-2581.

［2］王海霞.舰船组合导航信息综合集成技术应用研究［D］.哈尔滨：哈尔滨工程大学，2009.

［3］康叶伟，黄亚楼，孙凤池，等.一种基于RBUKF滤波器的SLAM 算法［J］.计算机工程，2008，34（1）：17-20.

［4］刘高峰.高速强机动目标跟踪算法及应用研究［D］.武汉：华中科技大学，2008.

［5］张园.空中单机动目标跟踪算法研究［D］.大连：大连海事大学，2014.

［6］张园，沈鹤鸣.卡尔曼滤波及其军事应用［M］.北京：国防工业出版社，2016.

［7］张园，郭晨，刘淑波，等.基于S修正卡尔曼滤波的自适应网格模糊交互多模型算法研究［J］.舰船科学技术，2014，36（3）：13-18.

［8］ZHANG Y，GUO C，HU H，et al.An algorithm of the adaptive grid and fuzzy interacting multiple model［J］.Journal of Marine Science and Application，2014，13（3）：340-345.

［9］刘德虎，周希辰，匡华星.一种修正的自适应网格交互多模型算法［J］.火力与指挥控制，2014，39（1）：79-82.

［10］郑雅聪.基于交互式多模型的机动目标跟踪算法研究［D］.石家庄：石家庄铁道大学，2014.