基于ReliefF特征加权的人工蜂群聚类算法*

龙金辉，叶阳东

（1河南机电职业学院，郑州 451191；2郑州大学信息工程学院，郑州 450052）

0 引言

聚类分析是非监督模式识别中的重要分支，已经被广泛应用于人工智能、模式识别、计算机视觉和模糊控制等许多领域［1-5］。聚类分析处理数据方法就是将数据集合依据某种相似度标准划分为若干数据的子集，力图使该数据集中具有相似特征的数据划归为同类。

模糊聚类算法最初由Dunn提出，后被Bezdek等人加以扩展，由于模糊聚类算法模式简明有效，引发了许多学者的研究兴趣。通过对模糊聚类算法的大量研究，学者们发现了算法存在的一些问题，诸如聚类数目难以确定、对初始值敏感、迭代难以取得全局最优、对噪声敏感等。针对这些问题各种改进方法的不断提出，对模糊聚类算法的研究也日趋深入。

模糊聚类算法没有度量各维特征对聚类结果的贡献程度，针对这个问题，一些学者提出了基于特征加权的聚类算法。文献［6］提出了一种改进模糊聚类算法，通过引入隶属度约束函数，得到了数学含义明晰的隶属度迭代公式，从而使得算法运行时的迭代次数显著减少；可能性模糊C-均值聚类算法（Possibilistic Fuzzy C-means）［7］和 IPCM 算法（Improved Possibilistic C-Means）［8］可以解决一致性聚类问题，然而算法收敛速度较慢。文献［9］提出了一种基于特征加权的模糊聚类算法，通过ReliefF算法对特征进行加权处理，使样本数据的聚类效果得以改进，文献［10］提出了改进模糊划分的FCM聚类算法GIFP-FCM，该算法比FCM算法具有更好的参数适应性。

人工蜂群算法（Artificial Bee Colony，ABC）是Karaboga于2005提出并加以拓展的一种群体智能优化算法［11］，该算法模拟了蜂群的群体行为。人工蜂群算法思想方法简明有效，同时算法又具有相应的理论基础。该算法在函数优化、聚类分析以及一些工程项目应用等领域取得了较好的应用效果［12-14］。人工蜂群算法主要特点是算法在确定的解决方案运行中需要循环比较对解决问题的可能解的优劣并择优，将各种蜜蜂个体的局部寻优行为以及蜜蜂群体中的全局寻优行为相结合，从而找到最优的可能解。

本文提出一种基于特征加权的人工蜂群聚类算法，算法对蜂群进行初始化，使得初始蜂群在解空间中覆盖面广泛，随着迭代次数增加，使蜜蜂在迭代过程中尽可能在各种可能区域进行搜索，侦察蜂的随机搜索尽可能有效地跳出局部最优从而找到全局最优解，兼顾算法的局部搜索能力与全局搜索能力。利用特征加权算法ReliefF对特征属性进行度量，求出特征属性集中每一特征属性的权重，使得各个特征能够明显反映出其聚类样本的贡献。根据权值大小对数据样本进行处理并进行聚类分析。本文将ReliefF特征加权与人工蜂群聚类算法相结合，旨在提高聚类算法的综合性能。

1 Relieff算法与FCM算法

1.1 Relieff算法

基本的Relief算法是 Kira和Rendell在1992年提出的［15］，经过扩展所得到的ReliefF算法可以解决多类问题，ReliefF算法基本思想是求取特征属性集中每一特征属性的权重。突显权值较大特征聚集同类样本的作用。

设diff_miss是N×1矩阵，表示mij与xi在特征上的差异。

P（l）为l类出现的概率，由第l类的样本个数除以数据集中样本的总个数。ReliefF算法中Weight由下式更新

如此循环执行指定次数，从该算法可以得到每一个特征的权重。

1.2 模糊c均值聚类算法（Fuzzy C-Means，FCM）

目标函数为：

其中，dij为第i个聚类中心与第j个样本点的距离。

在满足式约束条件下使得目标函数达到最小值。根据拉格朗日乘数法，得出目标函数取得最小值的必要条件为：

步骤1：在区间［0，1］内随机初始化隶属矩阵；

步骤2：根据式（6）计算聚类中心；

步骤3：根据式（5）计算目标函数，如果相对上次目标函数值的改变量小于确定的阈值，算法停止；

步骤4：根据式（7）更新隶属矩阵，转到步骤2。

1.3 WFCM 算法（Weighted Fuzzy C-Means）

采用欧式距离度量的模糊聚类算法对不同特征属性聚类结果的影响因素没有深入探讨。各个特征属性对聚类的影响是不同的。所以需要度量各个特征属性对聚类结果的贡献程度，求得数据对象的每一维特征的权重，然后再进行聚类。将特征加权引入到模糊聚类算法中，其目标函数可定义如下：

1.4 人工蜂群算法（Artificial Bee Colony，ABC）

人工蜂群算法由3种蜂构成：采蜜蜂、观察蜂和侦察蜂。采蜜蜂负责探索蜜源并为观察蜂提供信息；观察蜂依据分享的信息决定是否开采蜜源；侦察蜂随机搜索新的蜜源。蜂群中一半是采蜜蜂，一半是观察蜂。开采完蜜源的采蜜蜂将会转变为采蜜蜂。蜂群智能行为可以概括如下：初始阶段，采蜜蜂随机在蜂巢附近搜索蜜源。找到蜜源后，蜜蜂成为采蜜蜂并对该蜜源进行开采，采蜜蜂返回蜂巢卸下蜂蜜，然后在舞蹈区通过跳摇摆舞将蜜源信息分享给观察蜂。如果蜜源已开采完，采蜜蜂就成为侦察蜂，并随机搜索新的蜜源。等待在蜂巢的观察蜂依据蜜源质量选择更好的蜜源。在人工蜂群算法中，蜂群的搜索范围覆盖了优化问题的所有可能解，采蜜蜂所开采的随机蜜源位置对应了解决问题的一个可能解，蜜源的花蜜量对应了解的适应度函数值。采蜜蜂或观察蜂的数量对应了解的个数。该算法的基本实现流程如下：

首先，人工蜂群算法根据式（9）随机地生成N个侦察蜂的初始蜂群，即初始解，N也是采蜜蜂的数量，同时也是蜜源数量。每个解是一个D维向量，表示求解的优化问题维度。

随后进行算法的迭代，采蜜蜂在当前位置附近展开邻域搜索，产生一个新位置，如式（10）所示：

采蜜蜂在采蜜时采用贪婪原则，将已经找到的最优解和邻域搜索解进行比较，当搜索解优于已经找到的最优解时，替换记忆解；反之，保持不变。

在所有的采蜜蜂完成邻域搜索后，观察蜂根据轮盘赌原则选择采蜜蜂，适应度大的采蜜蜂吸引观察蜂的概率大于适应度小的采蜜蜂，这样可以充分搜索到质量较好解，随后每一个观察蜂根据式（10）对采蜜蜂进行邻域探索。

在人工蜂群算法中，观察蜂选择采蜜蜂的概率Pi由式（11）计算：

其中：fiti为第i个解的适应度，对应于蜜源的丰富程度，花蜜量越丰富，被选择的概率越大。

为防止算法陷入局部最优，在每次迭代过程中，记录每个采蜜蜂的适应度值，若经过limit次循环适应度值没有改进则放弃该解，由采蜜蜂根据式（10）产生新的位置代替该解。

在全部迭代次数maxCycle完成以后，将适应度最大的最优解作为最终得到的结果。

2 基于ReliefF特征加权的人工蜂群聚类算法（WABCFCM）

本文提出的算法，蜂群中的蜜蜂担任不同的角色进行协同工作。首先对蜂群进行初始化，使得初始蜂群在解空间中覆盖面广泛，使蜜蜂在迭代初期进行各种可能区域的搜索，侦察蜂的随机搜索尽可能有效地跳出局部最优从而找到全局最优解。为了取得更好的聚类效果，通常需要度量各维特征属性对聚类的贡献程度，对聚类越有利的特征属性其权值也应该越大；利用特征加权算法ReliefF对特征属性进行度量，求出特征属性集中每一特征属性的权重，使得各个特征能够明显反映出其聚类样本的优势；最后，根据权值大小对数据样本进行处理并进行聚类分析。本文将ReliefF特征加权与人工蜂群聚类算法相结合，旨在提高聚类算法的综合性能，算法具体概括如下。

步骤1：初始化种群参数，包括采蜜蜂、观察蜂和侦察蜂的数量，最大迭代次数maxCycle，搜索次数 limit，聚类数 c；

步骤2：随机产生初始聚类中心，计算所有蜜蜂的适应度函数值，根据蜜蜂的适应度进行排序，将前50%作为采蜜蜂，后50%作为观察蜂；

步骤3：令计数器初始值为1，循环开始；

步骤4：对采蜜蜂根据式（10）进行邻域搜索产生新位置，计算新的适应度值，采蜜蜂利用贪婪算法对旧位置和新位置进行择优；

步骤5：根据式（11）计算观察蜂与蜜源相关的概率值，对选取的观察蜂根据式（10）产生新位置，计算新的适应度值，观察蜂利用贪婪算法对旧位置和新位置进行择优；

步骤6：如果采蜜蜂、观察蜂搜索次数超过限定次数limit，仍然没有找到更高适应度值的蜜源，则放弃该蜜源，同时蜜蜂的角色由采蜜蜂或者观察蜂转化为侦查蜂，并随机产生一个新蜜源；

步骤7：记忆当前时刻适应度值最大蜜蜂位置；

步骤8：判断循环结束条件是否满足，如果满足，则适应度函数值最大的蜜蜂位置就是最优聚类中心；否则，计数器增加1，并跳转到步骤4；

步骤9：使用ReliefF度量各维特征权重，然后对数据样本加权后进行类别划分。

3 实验结果分析

为了验证基于ReliefF特征加权的人工蜂群聚类算法（WABCFCM）的有效性与可行性，分别采用FCM算法、WFCM算法、本文算法进行对比实验。实验环境为Windows XP操作系统，2.09 GHz处理器，2 G内存，程序运行环境为Matlab 2012 b。

采用UCI中的Iris数据集进行测试，该数据集通常用于测试算法性能。数据集由四维空间中的150个数据样本组成，每个样本有5个分量，分别表示Iris 数据集的 Petal length、Petal width、Sepal length、Sepal width和类标号。数据集含有Setosa、Versicolor和Virginical 3种类型，每个类型有50个数据样本。使用3种算法对该数据集进行聚类，本文算法参数的设置如下：蜂群个数：N=200，最大循环次数：max-Cycle=100，limit=30。采用聚类准确率（Accuracy，ACC）、归一化互信息（Normalized Mutual Information，NMI）、芮氏指标（Rand Index，RI）、运行时间等指标对3种算法性能进行综合评价。3种算法分别重复10次实验，所得各项指标取平均值，所得的测试结果如表1所示。

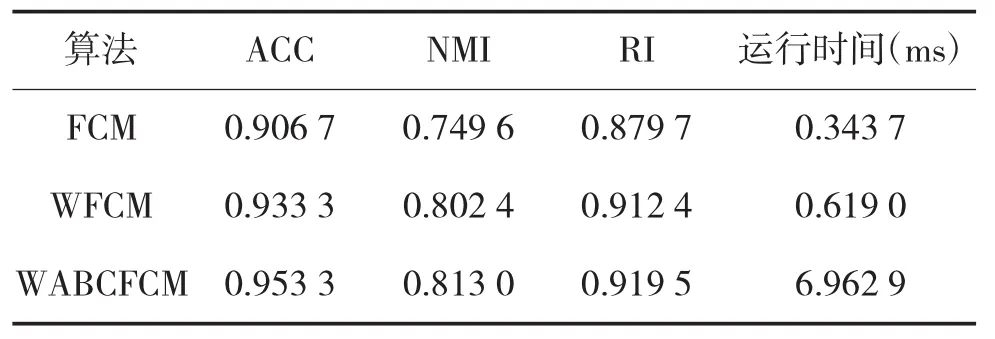
表1 Iris数据集的几种聚类算法对比

下页图1为Iris数据集取前二维样本点真实类型分布，图2为FCM聚类结果，图3为WFCM聚类结果，图4为WABCFCM聚类结果。

表2 几种算法聚类中心对比

在表1中，通过对比各项指标，首先可以看出本文提出的算法聚类准确率、归一化互信息与芮氏指标均要高于FCM和WFCM算法，尽管运行时间稍长；其次，再来对比聚类中心位置，文献［16］给出了测试数据集Iris的实际类中心的位置：p1=（5.00，3.42，1.46，0.24），p2=（5.93，2.77，4.26，1.32），p3=（6.58，2.97，5.55，2.02）。本文分别采用 WFCM 与WABCFCM对该数据集进行聚类，聚类中心如表2所示。从表中可知，WABCFCM算法得到的聚类中心更接近实际的类中心位置。图5为运行WFCM算法与WABCFCM算法所得特征权重，从图中可以看出第三维特征贡献最大，第四维特征贡献最小。

Wine数据集是一个用来测试算法在高维数据集的性能表现，其来源于葡萄酒，数据集含有178个数据样本，有13个特征属性值。所有数据样本分为3个类，这3类分别包含59、71、48个数据样本。下面对该数据集使用3种算法进行聚类，结果如表3所示。

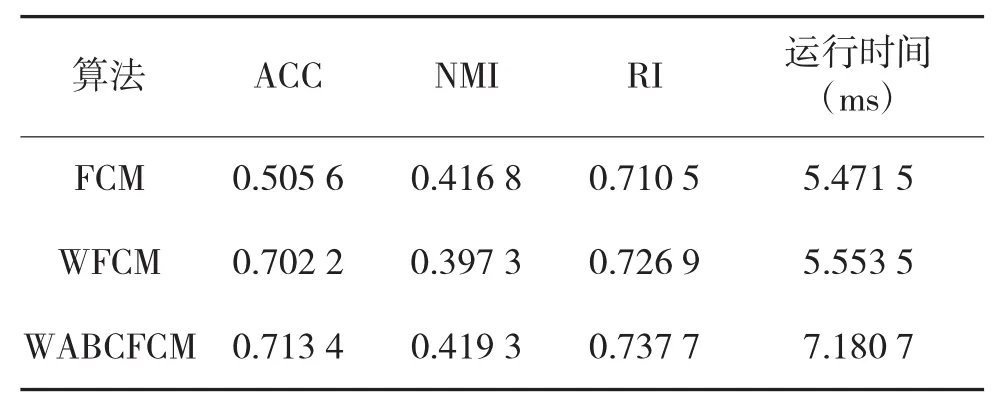
表3 Wine数据集的几种聚类算法对比

分析表3可以看出，对于高维数据集，WFCM算法同样要比传统的FCM算法优越，在聚类的准确率、归一化互信息、芮氏指标方面表现都比较好。图6为运行WFCM算法与WABCFCM算法所得特征权重，从图中可以看出第11维特征权重较小而第12维特征权重较大。

通过比较各项实验结果可知，本文算法在聚类准确率、归一化互信息、芮氏指标等方面有明显的改进，在UCI数据集上实验显示出了算法的优良性能，且多次实验结果也比较稳定，充分说明本文算法避免聚类中心局部收敛、提高聚类准确率以及算法的综合性能。

4 结论

本文提出了一种基于ReliefF特征加权的人工蜂群聚类算法，通过ReliefF度量数据集各维特征权重，弱化了冗余特征对聚类的干扰，强化了有效特征对聚类的贡献，利用人工蜂群中观察蜂对蜜源的全局搜索，找到的聚类中心位置更加接近实际位置，同时提高了聚类算法的综合性能。UCI标准数据集中实验结果表明了该算法具有较高聚类准确率、归一化互信息、芮氏指标。本文算法也存在着一些不足：能否在不确定k值的情况下提高聚类算法的综合性能等。如何解决这些问题将是下一步的研究方向。

［1］孙吉贵，刘杰，赵连宇.聚类算法研究［J］.软件学报，2008，19（1）：48-61.

［2］修宇，王士同，吴锡生.方向相似性聚类方法 DSCM［J］.计算机研究与发展，2006，43（8）：1425-1431.

［3］KIRINDIS S，CHATZIS V.A robust fuzzy local information c-means clustering algorithm［J］.IEEE Trans Image Process，2010，19（5）：1328-1337.

［4］CAI W，CHEN S，ZHANG D.Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation ［J］.Pattern Recognition， 2007，40 （3）：825-838.

［5］PAL N R，PAL K，BEZDEK J C.A new hybrid c-means clustering model［C］//Proc of the IEEE Int Conf on Fuzzy Systems，Piscataway：IEEE Press，2004：179-184.

［6］HOPPNER F，KLAWONN F.Improved fuzzy partitions for fuzzy regression models ［J］.Journalof Approximate Reasoning，2003，32（2）：85-102.

［7］PAL N R，PAL K，BEZDEK J C.A possibilistic fuzzy c-meansclustering algorithm ［J］.IEEE Trans Fuzzy Systems，2005，13（4）：517-530.

［8］ZHANG J S，LEUNG Y W.Improved possibilistic c-means clustering algorithms［J］.IEEE Trans Fuzzy Systems，2004，2（12）：209-217.

［9］李洁，高新波，焦李成.基于特征加权的模糊聚类新算法［J］.电子学报，2006，34（1）：89-92.

［10］朱林，王士同，邓赵红.改进模糊划分的FCM聚类算法的一般化研究［J］. 计算机研究与发展，2009，46（5）：814-822.

［11］KARABOGA D.An idea based on honey bees warm for numericaloptimization ［D］.Kayseri，Turkey：Erciyes University，2005.

［12］AKAY B，KARABOGA D.A modified artificial bee colony algorithm for real parameter optimization［J］.Information Sciences，2012，192（1）：120-142.

［13］KARABOGA D，OZTRUKC.An novel clustering approach：artificial bee colony（ABC）algorithm ［J］.Applied Soft Computing，2011，11（1）：652-657.

［14］刘路，王太勇.基于人工蜂群算法的支持向量机优化［J］.天津大学学报，2011，44（9）：803-809.

［15］KIRA K，RENDELL L A.A practical approach to feature selection ［C］//Proceedings of the 9th International Workshop on Machine Leaning.San Francisco，CA：Morgan Kaufmann，1992：249-256.

［16］HATHAWAY R J，BEZDEK J C.Nerf C-means：Non-Euclide-an relation fuzzy clustering ［J］.Pattern Recognition 1994，27（3）：429-437.