建构反应题中能力估计准确性的影响因素：评分者人数和项目个数的交互作用

孙小坚，康春花，曾平飞，辛 涛

(1.北京师范大学中国基础教育质量监测协同创新中心，北京 100875；2.浙江师范大学教师教育学院，金华 321004)

1 前言

建构反应题(Constructed Response item，CR题)因其可以对个体的分析、综合、应用等能力进行较为准确地测量(康春花，辛涛，2010)，受重视程度也日益增加。但由于CR题没有统一的标准答案，因此需要额外的评分人员对学生的作答进行评分，而各评分员由于其自身的知识、能力、经验和情绪状态的不同，导致CR题的评分误差相对较大(Attali，2014；Kim，Walker，& McHale，2010；周群，2007)，以及不同评分员之间的误差也各不相同(田清源，2006)。如此，评分者信度问题将受到一定程度的挑战。如何一方面保证学生能力估计值的准确性，另一方面分离出评分者宽严度等随机误差的大小及其影响因素是当前研究的一个重要问题。

目前，从测量学的角度，主要通过多水平模型来分离学生能力水平、评分误差及其影响因素，从而达到对学生能力特质更为精确的估计，如多水平随机系数模型(Multilevel Random Coefficient Model，MRCM)，广义分部评分多水平侧面模型(G-MLFM；Wang & Liu，2007)。然而，MRCM是线性模型，而G-MLFM不适于继时性加工的任务情境(Andrich，1995；Tutz，1990)。为此，康春花等(2016)将多面Rasch模型、多水平模型和等级反应模型(GRM)三者结合，构建了等级反应多水平侧面模型(Grade Response Multilevel Facets Model，GR-MLFM)，并通过两个模拟研究探讨了GR-MLFM的返真性，结果表明：模型可以很好地估计出被试参数、项目参数和评分者参数，具有较好地适用性和可行性。GR-MLFM兼具多面Rasch模型、MRCM和GRM的特征，可用于CR题如数学应用题问题解决，公式推导等逻辑性强，解法多样的评分情境，以考察评分者的宽严度及其相关的影响因素。根据GR-MLFM的特征，不难看出，在对CR题评分数据的分析中，影响GR-MLFM能力参数估计准确性的因素主要有被试特质、项目特质和评分者特质，而评分者特质又可包括评分者人数多少及评分者个人特质如评分经验、人格特征等。

就被试特质而言，研究认为被试作答态度的随意性和偶然性会影响其能力估计的准确性，偶然性作答分为两种情况，一种是低能力被试答对较难的项目，另一种是高能力被试答错较容易的题目，这两种情况的出现均会影响对被试能力估计的准确性(戴海崎，简小珠，2005；Wright，1977)。关于项目特质，有研究指出，在不增加评分者人数的情况下，通过增加测验项目数便可以提高被试能力估计的准确性(Decarlo，2010；Decarlo，Kim，& Johnson，2011；Kim，2009)。而在评分者特质方面，有研究指出(Hombo，Donoghue，& Thayer，2001；Linacre，2007；Wolfe，2004)，在固定项目个数的前提下，通过增加每个项目上的评分者人数则可提高能力参数估计的准确性。此外，评分者的评分经验、人格特质等也会影响其评分的准确性，从而间接影响了对被试能力估计的准确性(Wolfe，2004)。

由上可以看出，以往研究对多水平IRT模型在被试能力特质估计准确性的影响因素上有所涉及，但在探讨评分者人数和项目个数对被试能力估计准确性时，只对其中的一个因素进行分析，将另一个因素作为控制变量。而实际上，不同的题目个数或测验长度，所需的评分者人数是否也存在不同？是否无论题目个数的多少，只要增加评分者人数就可达到准确估计的目的？为找到问题的答案，为主观题测验编制及评分设计提供有用信息，节约考试成本，研究拟基于GR-MLFM的模拟设计，进一步探讨项目个数与评分者人数对被试能力估计准确性的影响模式。

2 方法

2.1 研究目的

采用康春花等(2016)提出的GR-MLFM探讨项目个数和评分者人数对被试能力估计准确性的影响，以期为测验的组织者在项目个数和评分者人数的选择上提供参考。

2.2 研究模型

考虑到研究主要关注被试的能力估计准确性的问题，研究将使用GR-MLFM中的评分者固定效应模型，其公式如下

水平1公式：

(1)

水平2公式：

Bij=γijDr=γr

(2)

将式(1)和式(2)进行整合，得到：

(3)

2.3 模拟设计

2.3.1 评分情境

考虑到完全交叉设计在小规模评价中经常使用(Muckle & Karabatsos，2009；钟晓玲，康春花，陈婧，2013)，故研究以该设计为例。50个被试作答2到5个项目，同时2到5个评分者对所有被试的作答情况进行1到4级的评定，1表示作答情况非常差，4则表示作答情况非常好。

2.3.2 实验变量

研究采用4 × 4的被试间实验设计。自变量有两个：项目个数(2个、3个、4个、5个)和评分者人数(2人、3人、4人、5人)。因变量有4个，分别为能力估计值与真值的相关r、偏差(Bias)、平均绝对偏差(Mean Absolute Bias，MAB)和误差均方根(Root Mean Square Error，RMSE)。

2.3.3 参数设定

模型涉及到被试、项目和评分者三个层面的参数，各层面的参数设定如下：

被试参数：设定被试总体的能力均值为0，即γ00=0，各被试随机效应从标准正态分布N(0，1)中随机抽取。

项目参数：(1)为保证模型可被识别和方便设计，项目1的区分度参数固定地设置为1，而剩余的项目区分度则从对数标准正态分布中随机抽取。(2)项目难度参数则从标准正态分布中抽取，考虑到每个项目均有3个难度阈值，此时将逐个生成项目的难度参数，具体过程为：针对第一个项目，从标准正态分布中随机抽取3个值，之后对这3个值由小到大进行排序，最后将排序后的3个值分别作为该项目的第1、2、和第3个难度阈值。其它项目的难度参数也依此步骤依次生成。

评分者参数：Muckle和Karabatsos(2009)将Dr=1和Dr=-1 分别称为评分者中等严格和中等宽松。研究将评分者参数限定在此区间内并进行细分，具体的宽严度为D=(-1，-0.5，0，0.5，1)，而各评分者的具体宽严度值将从该向量中随机抽取。

2.4 数据生成

被试的作答反应数据将通过R软件自编程序实现。具体步骤为：(a)从标准正态分布N(0，1)中生成50名被试的能力值；(b)根据2.3.3章节中关于项目和评分者参数的设定方法生成相应的参数；(c)将生成的被试、项目和评分者参数代入到公式(3)中，计算相应的累积概率和类别概率；(d)将(c)中得到的累积概率和从均匀分布U(0，1)中生成的随机数进行比较，如果该随机数小于第一个累积概率，则令随机数为1，若随机数在第一个和第二个累积概率之间，则令随机数为2，以此类推，最终得到所有评分者对于所有被试在所有题目上的作答数据。为减少抽样误差，每种实验条件均重复50次。之后用R2OpenBUGS程序包在R软件中调用OpenBUGS软件进行参数估计，最终的估计值为50次估计值的均值。

2.5 评价标准

拟合指标有4个：估计值与真值间的相关r、偏差(Bias)、平均绝对偏差(MAB)和误差均方根(RMSE)。其中相关系数r反映能力估计值与真值间的相互关系及方向；偏差则反映估计值与真值之间的系统误差(de la Cruz，1996)，越接近于0越好；MAB和RMSE则用于测量估计值与真值之间的整体误差(Wetzel，Böhnke，& Rose，2016)这两个指标则是越小越好。各指标的计算公式为：

3 结果

3.1 估计值与真值的相关

表1呈现了各实验条件在50次重复试验下各被试能力估计值与真值相关系数的描述统计量。由表可知，总体而言，随着项目个数的增加，估计值与真值间的相关程度不断加强，并且最大值与最小值之间的差距也在不断缩小，且该趋势不受评分者人数的影响。再者，当项目个数和评分者人数均为2个时，估计值与真值之间的相关最低，且其标准差最大(SD=0.051)，说明二者间的相关有比较大的波动，该波动可从其变化范围给予验证。当然，需要注意的是当只有2个项目时，4种评分者人数条件下的能力估计值与真值的相关均在0.80以下，说明当项目个数相对较少时，被试能力估计值与真值差异较大，且不易受评分者人数的影响。此外，当项目个数为5个时，在4种评分者人数条件下被试能力真值与估计值间的相关均在0.90以上，且在4个评分者时达到所有条件下的最大相关(0.98)，说明此时被试能力估计值与真值间的关系最为密切。

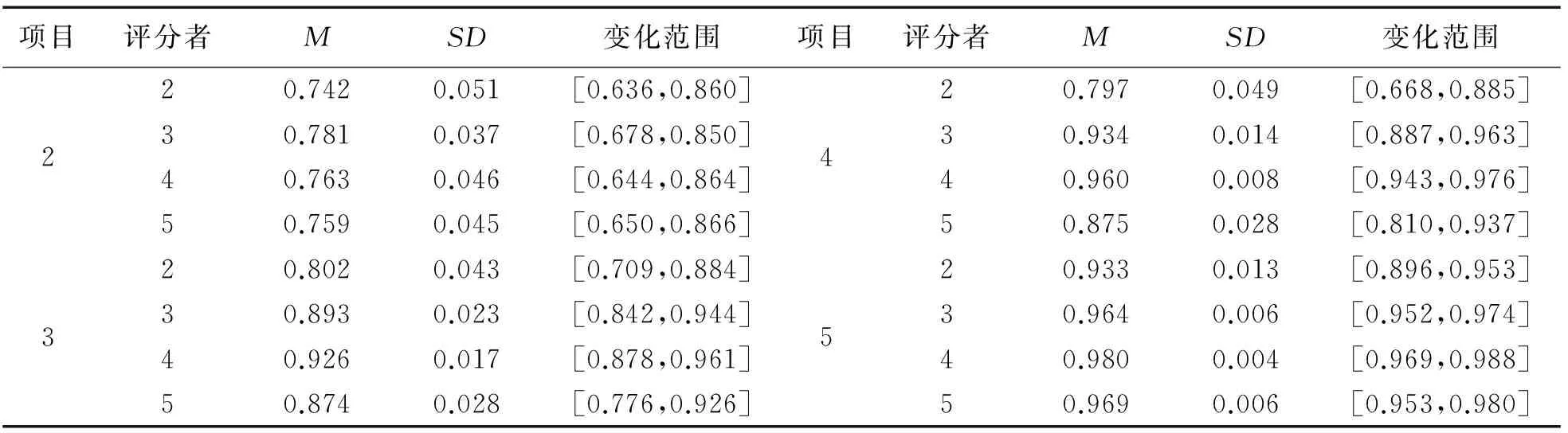
表1 各实验条件下的相关系数的描述统计结果

3.2 估计值与真值的Bias

表2为各条件下的偏差统计结果。表中的结果显示，在所有16种条件下，大部分条件下的偏差值为负值(10个)，说明大多数条件下被试的能力值被低估。同时，不同项目个数下，各偏差值的范围分别为：-0.083 ～ 0.135，-0.289 ～ 0.055，-0.134 ～ 0.124，以及-0.183 ～-0.101。可见，3个项目条件下的偏差变化最大，且大部分的偏差值均为负数，说明该条件下的被试能力易被低估。当具体到每一个条件时，2个项目和2个评分者组合下的偏差变化范围最大(全距=2.584)，且偏差的SD也是最大的，说明该条件下的能力估计值不稳定，模型无法较为准确地估计出被试的真实能力。其次，2个项目4个评分者组合下的偏差波动范围和SD标准也相对比较大，在该条件下，模型也较难估计出被试的真实能力。

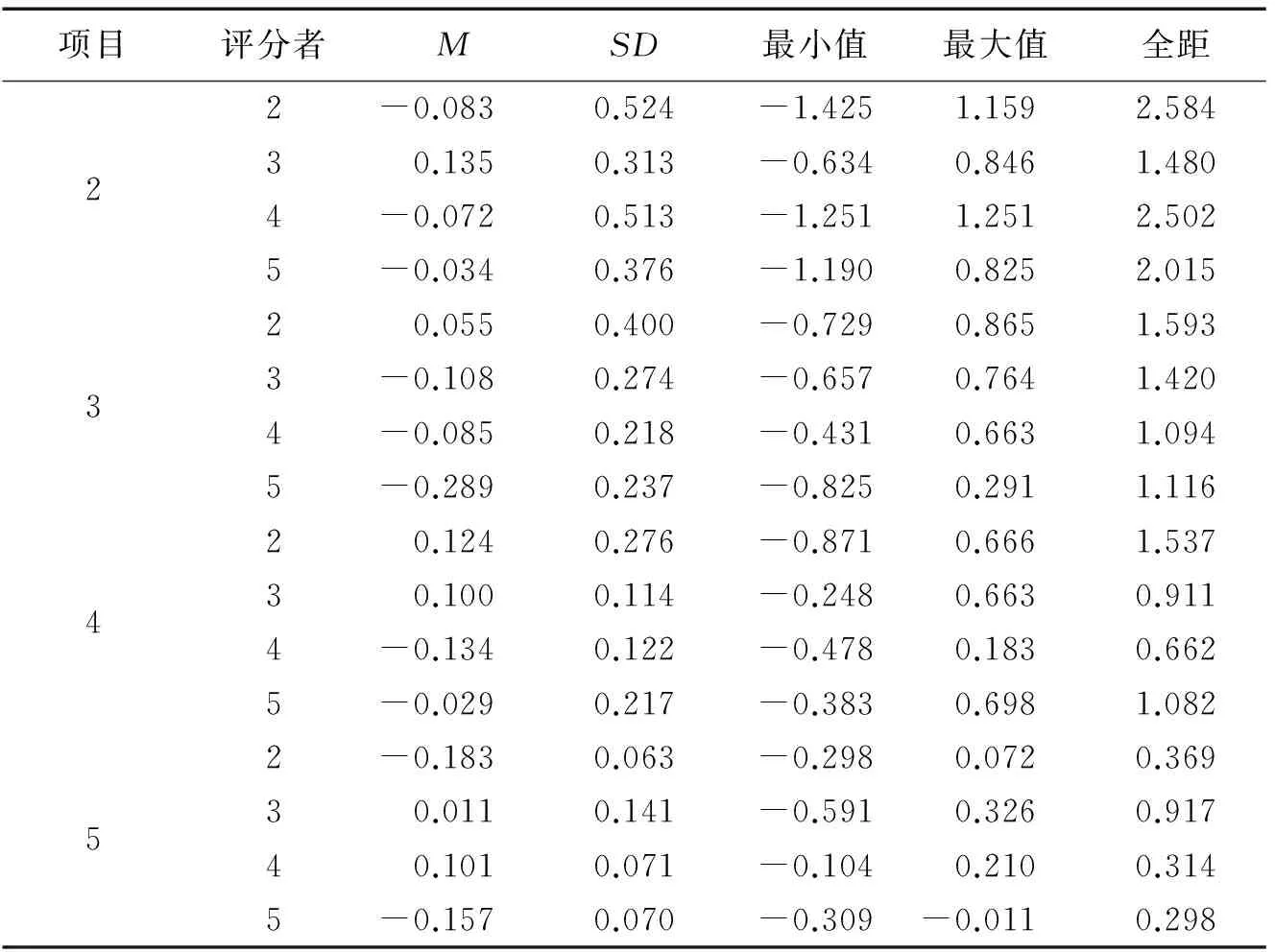
表2 各实验条件下的偏差估计结果

图1更为清楚地呈现了各组合条件下的偏差分布情况。由图可知，5个项目3个评分者时的偏差值最接近0，而3个项目5个评分者条件下的偏差离0值最远。此外，3个评分者和5个评分者在不同项目个数上的变化模式是一样的，均为先向下，后向上，最后再向下的变化趋势；而2个评分者和4个评分者的变化模式则相反：2个评分者的变化趋势是先向上，然后再向下；而4个评分者则是先向下，然后向上变化，并与2个评分者发生交叉。

图1 各实验条件下偏差值分布情况

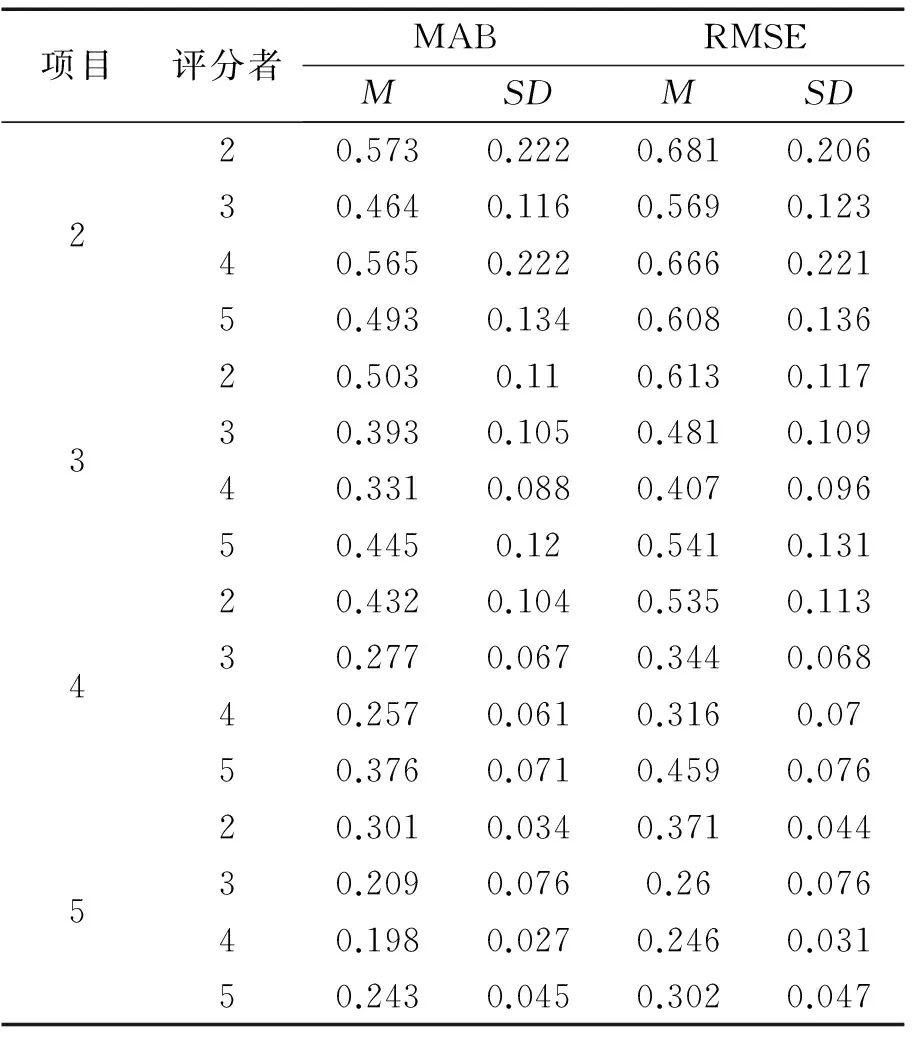
项目评分者MABRMSEMSDMSD220.5730.2220.6810.20630.4640.1160.5690.12340.5650.2220.6660.22150.4930.1340.6080.136320.5030.110.6130.11730.3930.1050.4810.10940.3310.0880.4070.09650.4450.120.5410.131420.4320.1040.5350.11330.2770.0670.3440.06840.2570.0610.3160.0750.3760.0710.4590.076520.3010.0340.3710.04430.2090.0760.260.07640.1980.0270.2460.03150.2430.0450.3020.047

3.3 估计值与真值的MAB和RMSE

表3呈现了被试的能力估计值与真值在50次重复条件下MAB和RMSE的描述统计量。由表3可知，5个项目4个评分者组合下的MAB和RMSE的均值和标准差均最小，而2个项目2个评分者组合下的MAB和RMSE的均值最大。各实验条件下的两个指标的标准差均比较小(分别为：0.027～0.222和0.031～0.221)，说明两个指标在50次试验下的估计结果相对比较稳定。同时，各条件的RMSE和MAB的相对位置和发展趋势是一致的。

方差分析的结果发现，RMSE的分析结果与MAB的结果大致相同，故研究只呈现MAB的结果。表4呈现了被试能力估计值的MAB的方差分析结果。由表4可知，评分者变量和项目变量二者均存在显著的主效应；并且二者的交互效应也显著，其效果量(ηp2)达到了中等效果量的标准(Cohen，1988)。

表4 能力估计值的MAB方差分析结果汇总表

由于评分者和项目个数二者间存在交互作用，有必要对它们进行简单效应分析，二者的交互效应见图2。经简单效应分析发现评分者人数在项目个数上的简单效应均显著(2个项目：F(3，196)=4.407**，ηp2=0.063；3个项目：F(3，196)=23.714***，ηp2=0.266；4个项目：F(3，196)=56.477***，ηp2=0.464；5个项目：F(3，196)=44.514***，ηp2=0.405)；同时，不同评分者人数在各个项目个数条件下的多重比较结果发现：2个项目情况下，2个评分者和4个评分者间的MAB不显著，3个评分者和5个评分者间的MAB不显著，其它的多重比较结果均存在显著差异(此时，3个评分者时的能力估计准确性最高)；3个项目情况下，不同评分者人数间存在显著差异，此时MAB由小到大为4个、3个、5个和2个评分者；再者，在4个和5个项目情况下的MAB值由小到大的顺序与3个项目情况MAB的顺序相同，但无论是在4个还是5个项目情况下，4个评分者和3个评分者之间的差异均不显著，而在其它评分者多重比较中(如2个VS. 3个、4个和5个评分者；5个VS. 3个和4个评分者)存在显著差异。另一方面，项目个数在不同评分者人数也存在显著的简单效应(2个评分者：F(3，196)=36.631***，ηp2=0.359；3个评分者：F(3，196)=75.356***，ηp2=0.536；4个评分者：F(3，196)=84.555***，ηp2=0.564；5个评分者：F(3，196)=59.974***，ηp2=0.479)，并且在4种不同评分者人数上均表现出项目个数越多表现越好的趋势。

图2 评分者人数与项目个数的交互效应

4 讨论

作为教育与心理测验中常用的考试题型，CR题评分的准确性会影响被试的测验分数，而评分者效应作为CR题评分中的系统误差(Scullen，Mount，& Goff，2000)，该效应的出现一方面降低了评分者的信度，另一方面将极大地影响被试能力估计值的准确性。研究在前人的基础上将评分者人数和项目个数两个变量同时加以考虑，并使用康春花等(2016)提出的GR-MLFM来探讨此二者的不同水平对被试能力估计准确性的影响。

4.1 项目个数越多能力估计准确性越高

通过模拟研究发现，随着项目个数的增加，估计值与真值间的相关系数逐渐增大，该趋势不受评分者人数影响，而偏差、MAB以及RMSE三个指标均不断减小，说明被试能力估计的准确性在不断增加，该结果与前人的研究结果及论断相一致(Decarlo，2010；Decarlo，Kim，& Johnson，2011；Kim，2009)。该结果是可理解的，教育与心理测验中，项目可以看作是测量被试潜在能力的外部行为指标，被试在项目上的作答反应是其能力的外在表现。IRT中，测验所包含的项目数越多，测验的标准误就越小，则对被试能力的掌握情况越清楚，从而对其能力的估计就越发的精确(罗照盛，2012)。

4.2 项目个数不同，则所需评分者人数不同

事后分析的结果表明，随着项目数的增加，评分者人数与能力估计准确性之间呈倒U关系。当被试作答的项目数比较少时，3个评分者的评分结果相对较好，此时被试的能力估计值比较准确；而当项目个数增加到3个时，4个评分者可以得到最优的能力估计值；此后，随着项目个数的增加，3个和4个评分者得到的被试能力估计准确性并没有显著性差异，但此二者与1个和2个评分者条件下均存在显著差异。此结果与前人的研究结果并不一致，前人的结果表明被试能力估计的准确性随着评分者人数的增加而不断提高(Hombo et al.，2001；Linacre，2007；Wolfe，2004)。出现不一致结果的原因可能是变量设置上的差异，前人的研究(如Hombo et al.，2001)主要是在控制项目个数的情况下，探讨评分者人数对被试能力估计准确性的影响，得出评分者人数越多估计越准确的结论。但正如研究得出的结果所示，评分者人数与项目个数之间具有交互作用，如此，若只考虑评分者人数对能力准确性的影响，其结论可能有失偏颇。

与此同时，研究的结果也有较大的实践意义。实际条件下，人们若为了提高被试能力估计的准确性而无限制地增加评分者人数，该做法将极大地增加测验的成本，不利于测验的发展。而本研究则说明，提高被试估计的准确性并不需要不断增加评分者人数，只需将评分者人数控制在一定范围即可。

4.3 研究展望

研究通过一个模拟研究得到了一些比较有指导作用的结果，同样研究还存在一些值得进一步研究的地方，主要表现在：(1)评分情境的研究。研究采用的是完全交叉设计，该设计要求所有评分者评定所有被试的所有作答，其相对于嵌套设计和混合设计来说，评分者的工作量比较大，所需的资源也比较多，故当测验的被试量较大时，该设计将变得较复杂和繁琐，因此未来研究有必要探讨在嵌套设计和混合设计下评分者人数与项目个数对被试能力估计准确性的影响。(2)项目参数的研究。研究使用2 ～ 5个项目进行研究，结果表明项目个数越多，能力估计准确性越好。那么，随着项目个数的继续增加，该趋势是否会一直持续下去？也是未来值得关注的重要问题。

5 结论

研究通过模拟研究探讨了项目个数和评分者人数对被试能力估计准确性的影响，得到以下几个结论：

(1)项目个数和评分者人数的主效应和交互效应均显著。

(2)无论评分者人数多少，被试能力估计值的准确性均随着项目个数的增加而提高。

(3)项目个数不同时，被试能力估计的准确性随评分者人数的不同而不同。项目数为2个时，3个评分者得到的准确性最高；随着项目数的增加，4个评分者得到的能力估计的准确性变得最高。

戴海崎，简小珠.(2005).被试作答的偶然性对 IRT 能力估计的影响研究.心理科学，28(6)，1433-1436.

康春花，孙小坚，曾平飞.(2016).基于等级反应模型的多水平多侧面评分者模型.心理科学，39(1)，214-223.

康春花，辛涛.(2010).基于 IRT 的评分者效应模型及其应用展望.中国考试，(08)，3-8.

刘红云，骆方.(2008).多水平项目反应理论模型在测验发展中的应用.心理学报，40(1)，92-100.

刘慧，简小珠，张敏强，熊悦欣.(2012).多水平 IRT 的发展与应用述评.心理科学进展，20(4)，627-632.

罗照盛.(2012).项目反应理论基础.北京：北京师范大学出版社.

田清源.(2006).主观评分中多面Rasch模型的应用.心理学探新，26(1)，70-74.

钟晓玲，康春花，陈婧.(2013).基于 CTT、 GT、 IRT 的评分者信度研究——以某届奥运会女子跳水决赛为例.考试研究，(05)，41-52.

周群.(2007).主观题评分标准研究.考试研究，(01)，005.

Andrich，D.(1995).Distinctive and incompatible properties of two common classes of IRT models for graded responses.AppliedPsychologicalMeasurement，19(1)，101-119.

Attali，Y.(2014).A ranking method for evaluating constructed responses.EducationalandPsychologicalMeasurement，74(5)，795-808.

Cohen，J.(1988).Statisticalpoweranalysisforthebehavioralsciences(2ed).Hillsdale，NJ：L.Lawrence Earlbaum Associates.

DeCarlo，L.T.(2010).Studies of a latent class signal detection model for constructed response scoring II：Incomplete and hierarchical designs.ETSResearchReportSeries，(1)，i-65.

DeCarlo，L.T.，Kim，Y.，& Johnson，M.S.(2011).A hierarchical rater model for constructed responses，with a signal detection rater model.JournalofEducationalMeasurement，48(3)，333-356.

de la Cruz，R.E.(1996).Assessment-biasissuesinspecialeducation：Areviewofliterature.ERIC Document Reproduction Service No.ED390246.

Hombo，C.M.，Donoghue，J.R.，& Thayer，D.T.(2001).A simulation study of the effect of rater designs on ability estimation.ETSResearchReportSeries，(1)，i-41.

Kim，S.，Walker，M.E.，& McHale，F.(2010).Investigating the effectiveness of equating designs for constructed-response tests in large-scale assessments.JournalofEducationalMeasurement，47(2)，186-201.

Kim，Y.(2009).Combiningconstructedresponseitemsandmultiplechoiceitemsusingahierarchicalratermodel.Unpublished doctoral dissertation，Columbia University，New York，NY.

Linacre，J.M.(2007).Auser’sguidetoFacets：Rasch-measurementcomputerprogram.Chicago.Online：www.winsteps.com/facets.htm(01.02.08).

Muckle，T.J.，& Karabatsos，G.(2009).Hierarchical generalized linear models for the analysis of judge ratings.JournalofEducationalMeasurement，46(2)，198-219.

Scullen，S.E.，Mount，M.K.，& Goff，M.(2000).Understanding the latent structureof job performance ratings.JournalofAppliedPsychology，85(6)，956-997.

Tutz，G.(1990).Sequential item response models with an ordered response.BritishJournalofMathematicalandStatisticalPsychology，43(1)，39-55.

Wang，W.-C.，& Liu，C.-Y.(2007).Formulation and application of the generalized multilevel facets model.EducationalandPsychologicalMeasurement，67(4)，583-605.

Wetzel，E.，Böhnke，J.R.，& Rose，N.(2016).A simulation study on methods of correcting for the effects of extreme response style.EducationalandPsychologicalMeasurement，76(2)，304-324.

Wolfe，E.W.(2004).Identifying rater effects using latent trait models.PsychologyScience，46，35-51.

Wright，B.D.(1977).Solving measurement problems with the Rasch model.JournalofEducationalMeasurement，14(2)，97-116.