群组发展模型——干预研究的新方法

吕浥尘 赵 然

(中央财经大学社会与心理学院，北京100081)

1 引言

心理学研究的目的是对心理与行为进行描述、解释、预测和控制(彭聃龄，2011)。其中控制是建立在描述、解释和预测的基础之上，对不利于发展的行为或心理状态实施干预。心理学研究者一直致力于干预研究，试图通过教育、咨询、知识普及等方式改善个体行为，促进个体的心理健康。

干预研究作为广义追踪研究的一种形式(刘红云，张雷，2005)，通常采用随机对照实验设计(Lee et al.，2014)，将被试随机分配到干预组和对照组，在干预前和干预后对被试进行多次的测量，关心干预组与对照组在平均水平和发展趋势的差异。研究者不仅关注干预的即时效果，也越来越关注干预的持续效果(Armitage，Rowe，Arden，& Harris，2014)，以及观测值的整体发展趋势、个体发展趋势及趋势中的个体差异等(李丽霞，郜艳晖，张敏，张岩波，2012)。

根据研究目标的不同，采用的数据处理方法也有所差异。重复测量方差分析侧重于总体平均发展趋势，而潜变量增长曲线模型(latent growth curve model，LGM)和多层线性模型(hierarchical linear model，HLM)除了总体平均发展趋势之外，同时注重个体发展趋势之间的差异(刘红云，张雷，2005)。唐文清、方杰、蒋香梅和张敏强(2014)统计了中国1982年至2013年发表的研究论文，发现2005年之前国内追踪研究主要运用t检验和重复测量方差分析追踪数据，2005年后多层线性模型、潜变量增长曲线模型等分析方法有所应用，开始关注个体间的发展差异。

上述模型均假设研究样本存在相同的发展轨迹，即内部同质(homogeneity)，大多数个体具有共同的发展轨迹。然而很多心理状态和行为的发展过程并不存在普适的变化趋势，这一假设并非总能满足(王孟成，毕向阳，叶浩生，2014)。

以未成年人加入不良团体的研究为例。当研究者认为个体是同质的，男生加入不良团伙的概率在个体间是相同的，则可以用一条曲线模拟发展轨迹，如图1中的左图所示。而群组发展模型分析发现，可以将群体进一步分为三个亚组(如右图所示)。其中，74.4%的青少年几乎不可能加入不良团伙，12.8%的青少年则是“青春期”组，而最后的一组为“童年”组占总体的12.8%(Lacourse，Nagin，Tremblay，Vitaro，& Claes，2003)。可以看出，群体中由此往往存在不同的发展轨迹。如果将个体视为同质，那么估计的概率会被“折中”。

干预研究也开始关注个体的异质性(heterogeneity)(Peer & Spaulding，2007)。Nagin(1999)提出群组发展模型*巫锡炜(2009)曾将其译为“组基发展建模”。(group-based trajectory model，GBTM)，用以识别群体内遵循不同发展轨迹的亚组，并描绘亚组成员的发展轨迹曲线。Eggleston，Laub和Sampson(2004)认为群组发展模型是一种潜类别分析(latent class analysis)，而纪林芹和张文新(2011)将其归为潜类别增长分析(latent class growth analysis，LCGA)。

图1 个体同质与个体异质发展轨迹对比

2 群组发展模型的异质性

正如上文所说，多层线性模型、潜变量增长曲线模型认为群体是同质的，而群组发展模型的基本逻辑是群体具有异质性，为了更好地说明个体异质性，接下来将具体讨论这三种模型的区别。

多层线性模型和潜变量增长曲线模型认为个体可能存在变异性，并对这种变异性进行检验(截距和斜率)，但是认为群体中的个体是同质的，群体只具有一般的发展轨迹。Morgan，Farkas和Wu(2011)使用多层线性模型分析儿童学习的发展轨迹，发现患有学习障碍或语言障碍的儿童与健康儿童在阅读测试的平均值和变化速率(斜率)上均存在差异，并用种族、性别和自尊水平等因素解释这种差异。

与上述两种模型不同，群组发展模型认为个体间的发展轨迹可能存在质性差异，可以将群体划分为不同的轨迹组(或亚组)，群体是一个包括有限个轨迹组的混合。其中轨迹组的划分是基于统计分析和相关理论获得的，并非依据研究者的事后分析或特定的划分标准而确定的。因此，群组发展模型具有一定的统计效度，能够区分个体差异中的随机变异和真实变异，可验证模型的拟合效果。群组发展模型更近于真实情况，在实际应用中具有重要的意义。对17～42个月婴儿的攻击性研究发现，可以划分为三个轨迹组。28%的婴儿属于“低攻击组”，攻击性较低近似没有；14%的婴儿具有较高的攻击水平，且不断提高，为“高攻击组”；大多数儿童(58%)则属于“中度攻击组”，具有适度的攻击性，缓慢上升(Tremblay et al.，2004)。并且不同亚组的发展轨迹不同，其预测变量和结果变量很可能也有所差异。

基于两个研究的对比可以发现，潜变量增长曲线认为群体是同质的，分组依靠于测量指标，关注不同类型儿童的平均轨迹，以及个体特征如何影响个体对平均轨迹的偏离。群组发展模型则关注个体间的差异，识别潜在的轨迹组，包括不同轨迹的形状、轨迹组间的差异、区别轨迹组成员的因素以及可能改变轨迹的事件等(Nagin，2005)。因此，这两种研究方法是互相补充的，而不是相互对立的。潜变量增长曲线适用于分析具有共同发展轨迹的心理现象或行为，或特定分组(如性别、种族等)的发展轨迹等研究。而群组发展模型可以发现群体中无法确定亚组的、潜在的、具有质性差异的发展轨迹，而且可以研究干预、转学等转折点对发展轨迹的影响。

王孟成、毕向阳和叶浩生(2014)指出，群组发展模型与潜变量混合增长模型(latent growth mixed model，GMM)是目前两种最常用也是影响最大的处理群体异质增长的模型。二者最大的区别在于，群组发展模型假定各轨迹组内的个体具有相同的发展轨迹，组间同质而组间异质，通过不同轨迹组之间的差异来估计发展轨迹中的个体变异。而潜变量混合增长模型在确定亚组轨迹的同时，允许发展轨迹的增长参数(截距、斜率等)存在亚组内变异(刘红云，2007)，模型的估计更加复杂。

3 基本模型的建立

3.1 建立似然函数

与传统的聚类分析不同，群组发展模型的基础是最大似然估计，基其本思想是通过参数估计使得所有观测数据发生的概率最大。群组发展模型认为总体是由有限个潜在亚组构成的，可以用有限个多项式函数进行表达。每个亚组的发展轨迹不同，其概率分布也会存在差异。因此观测值发生的概率依赖于个体i所属轨迹组j的概率分布，以及个体i属于该轨迹组的可能性πj。最大似然估计的目的就是得出令观测值发生概率最大的参数值。

轨迹组的函数是观测值关于时间的变化，必须要考虑到不同时间点间的关系，因此不得不提到群组发展模型的另一基本原理——条件独立假设(conditional independence assumption)。这一假设认为对于指定轨迹组j的每一个体，任意时间上测量值的分布独立于之前时间点的测量结果。虽然这一假设看似难以置信，当下的行为表现通常与之前的行为相关，但是条件独立性假设是假定个体的偏离程度之间互不存在相关。因此指定轨迹组j中观测值的概率分布函数是相互独立的，不包括之前的测量值的影响。

基于这两个原理，可以建立两个函数进行估计：(1)使用适宜的概率分布函数描述观测值发生的概率，(2)以时间为自变量建立函数定义观测值与时间的关系，从而将发生概率、观测值、时间和参数联系起来，进行参数估计。

3.2 确定轨迹组数和轨迹形状

群组发展模型中每个亚组均具有不同的轨迹趋势，亚组的数量也就是描述发展轨迹的函数数量。因此，组数会影响最大似然估计中的参数数量，每个亚组的具体轨迹形状，以及模型的拟合程度。所以建立群组发展轨迹模型的第一步，也是最具挑战的一步就是确定轨迹组组数J。

首先，要明确划分亚组的原则。群组发展模型假定轨迹组内同质而组间异质，组间的差异近似于群体差异。因此，划分亚组的目的是发现具有相似发展轨迹的亚群体。模型应该能够以尽可能简洁、有效的方式呈现群体中的差异(Nagin & Odgers，2010)。轨迹组的划分不仅依赖于统计标准，也要基于理论支持和一定的主观分析。

在群组发展模型中，用于评估模型拟合的指标包括贝叶斯信息标准(Bayesian information criteria，BIC)、赤池信息标准(Akaike information criteria，AIC)等，其中最常用的是贝叶斯信息标准进行轨迹模拟，BIC=log(L)-0.5klog(N)(L是模型的似然值，N是样本量，k是模型中参数的数量)，最高的模型最为适宜。利用BIC选择最佳拟合模型时，需要不断调整参数量，而参数量受到亚组数J和发展轨迹阶数两方面的影响。因此，Nagin(2005)提出选择最佳模型为两步：

第一步，预设方程阶数，估计模型的组数J。发展轨迹可以是零阶(平坦直线)，一阶(有斜率的直线)，二阶(曲线)或者三阶等等。其中二阶曲线能够反映出多样的发展趋势，较为灵活。三阶函数太为复杂，难以抓取特征。因此通常假设发展曲线是二阶的，从而确定组数。

第二步，组数确定的基础上，调整方程阶数使得轨迹拟合更优。例如，第一步发现4个二阶函数的轨迹组最优，但是其中一个轨迹组模型的标准差较大，或从经验上认为可能存在一个零阶轨迹，则进一步对比两个模型。在组数J确定的基础上进行微调，确定最为适宜的发展轨迹阶数。

3.3 后验概率及模型检验

群组发展模型建立之后，还需要检验模型的准确性，计算轨迹组分配的后验概率(posterior probability)，判断模型是否真实反映了样本数据的情况。

对于已经确定的模型，具有已知观测值的个体在组J的可能性即为后验概率。可以通过在组J出现观测值的概率计算而得，然后根据最大后验概率分配原则分派个体。

Nagin(2005)总结出四种检验模型准确率的具体方法，其中两种方法以最大后验概率分配的准确性为衡量标准，另两种方法则关注估计πi的准确度：

(1)轨迹组中个体的后验概率均值大于0.7；

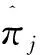
3.4 对轨迹组的概况描述

基于最大后验概率分配原则将个体进行分配，即可获得了每个轨迹组的成员构成。结合样本数据中的个体特征信息，就可以进一步对不同轨迹组进行简单描述。

通常采用交叉列联表的形式，不仅可以清晰呈现每个轨迹组中具有该特征的人员比例，而且可以比较不同轨迹组间的差异(如表1所示)。

需要注意的是，概况描述是基于后验概率之上的，而不是参数估计。概况描述只是描述性数据，缺乏统计检验，只能说明每个轨迹组的个体更倾向于具有哪些特点，无法证明这些特征会影响轨迹组的分配。在下一部分将会具体介绍如何进行统计检验，发现影响个体进入该轨迹组的因素。

表1 犯罪轨迹发展曲线的概况描述

注：来自于Nagin(2005)

4 干预研究中的应用

假设要研究记忆方法的干预对学生阅读理解能力的影响，如何分析这一方法的学习对学生发展轨迹潜在影响呢？在群组发展模型中，描绘群体中结果变量的分布具有两个核心指标——发展轨迹和人员分配比例πj。因此群组发展模型对干预的研究存在两种完全不同的逻辑。

一种研究逻辑是将干预视为预测变量(predictor)，探讨干预是否引起分组比例变化。其前提是认为轨迹稳定，干预只会改变个体所属的轨迹组，影响人员分配比例πj。因此关注干预是否能够预测分配比例πj。这种逻辑的核心在于，干预会引起质的改变(从轨迹组1到组2)。

另一种则认为干预是轨迹的转折点(turning point)，探讨干预是否改变了发展轨迹。这种思路认为人员分配比例πj是固定的，干预不会改变个体所属的轨迹组，而是直接影响整个轨迹组的发展轨迹。研究者关注干预前后轨迹趋势是否发生变化。因此，该逻辑倾向于认为干预会导致量的变化(轨迹的扭转)。

4.1 作为预测变量

正如3.4所说，不同轨迹组发展轨迹的描述性数据缺乏统计检验，不足以确定该特征是否能够预测分组。因此，确定预测变量需要进行进一步的参数估计。

发展轨迹是一个观测值的长期发展趋势。如果初始状态时变量X的水平能够估计个体未来的发展趋势，那么X则是一个预测变量。因此若研究者将干预视为一个预测变量，则干预应当在第一次测量之前。

从统计分析上而言，当个体i在变量X上的水平xi能够有效预测人员分配比例πj，则变量X为预测变量。因此建立函数关系πj(xi)，用Logit分布函数进行参数估计。对于具有J个轨迹组的模型，需要选择一个固定的对照组，对照组的参数设定为零，对其他J-1个轨迹组的参数进行Z检验。要进一步比较J-1个轨迹组间的差异，可采用Z分数检验或Wald检验。

4.2 作为转折点

当把干预视为发展轨迹的转折点时，干预发生在发展轨迹的时间区间内，基于干预之前的发展趋势进行对比。如果轨迹发生了变化，则说明干预使发展轨迹发生了偏离，干预对观测值存在一定影响。这也是在干预研究中使用群组发展模型的优势之一。

除此之外，此时干预前后的比较是轨迹组内的，均都具有相似的发展历程，个体是同质的。并且群组发展模型有助于发现发展轨迹和干预的交互作用，即干预对不同轨迹组的影响差异。但是需要注意，在群组发展模型中，是否参与干预往往不是随机分配的，因此不能获得因果结论，难以确定参与干预和结果变量之间的因果关系。

当把干预作为轨迹的转折点，考察事件(或干预)Z对发展轨迹的影响时，需要建立事件Z和发展轨迹的关系，即重新建立关于时间的多项函数。

综上所述，根据研究者关注的内容和干预的程度，可以采用不同的方法进行分析。如图2所示，若认为干预会引起质的改变，则作为预测变量X，探讨干预对分组的影响；如果只是发生量的变化则将其视为转折事件Z，研究干预如何影响发展轨迹。

图2 干预研究总模型

5 未来发展

Nagin和Land(1993)为了研究人群中犯罪行为的异质性提出了一种统计方法，渐渐发展为群组发展轨迹模型，并尝试将其应用于各个领域，对模型不断扩展。为了解决干预研究中非随机分组问题，可以将群组发展模型与倾向分数模型(propensity score modeling)相结合，促进因果推断的获得(Haviland，Nagin，& Rosenbaum，2007)。另外还提出了双轨迹模型用以分析同时发展的两个结果变量(Nagin & Tremblay，2001)，以及多轨迹模型(Nagin，2005)。近年来，群组发展模型的应用主要围绕着犯罪领域(Ward et al.，2010)，在干预研究中的具体应用还较为缺乏。

目前有两个成熟的插件用于分析群组发展模型：SAS程序的Proc TRAJ模块(Jones & Nagin，2007)和Stata软件的Traj插件(Jones & Nagin，2013)，都可以从http：//www.andrew.cmu.edu/user/bjones免费获得。

5.1 模型优势

(1)群组发展模型关注个体的异质性，能够识别群体中具有相似发展轨迹的个体，发现群体中典型的和非典型的发展历程(Nagin & Odgers，2010)；

(2)基于统计分析和相关理论划分轨迹组，而不是根据特定的分组标准(如性别、种族)或事后分析，具有一定的统计效度，能够区分个体的真实变异和随机变异；

(3)可以将干预作为预测变量或转折事件进行分析，从不同角度考察干预作用。作为转折事件进行分析时，在轨迹组内进行比较能够发现干预前后轨迹的变化，以及干预对不同轨迹组的影响差异。

5.2 应用局限

(1)群组发展模型是对纵向数据的分析，因此对缺失值的处理也是影响群组发展模型一个重要问题。虽然有相关的统计方法和模型有助于解决缺失值问题(Haviland，Jones，& Nagin，2011)，但是缺失值的存在或多或少都会影响模型的可靠性。

(2)群组发展模型需要足够的被试量。当被试较少时，观察值较少，往往难以发现群体中比例较小的轨迹组。研究发现当样本量超过200之后，轨迹组的划分趋于稳定(Nagin & Piquero，2010)。

(3)轨迹组的划分和轨迹形状是非固定的，没有最完美的模型。追踪时间长短也会影响轨迹的拟合。

综上所述，群组发展模型可以发现群体中无法确定亚组的、潜在的、具有质性差异的发展轨迹，获得不同轨迹组的分配比例和轨迹形状，更接近生活实际。而且能够获得干预前后轨迹组的变化情况，以及对不同轨迹组的影响差异。因此群组发展模型对干预研究效果的检验具有重要意义，可以有效出识别干预效果最好的群体，进行针对性的干预。

纪林芹，张文新.(2011).发展心理学研究中个体定向的理论与方法.心理科学进展，19(11)，1563-1571.

李丽霞，郜艳晖，张敏，张岩波.(2012).潜变量增长曲线模型及其应用.中国卫生统计，29(5)，713-716.

刘红云，张雷.(2005).追踪数据分析方法及其应用.北京：教育科学出版社.

刘红云.(2007).如何描述发展趋势的差异：潜变量混合增长模型.心理科学进展，15(3)，539-544.

彭聃龄.(主编).(2011).普通心理学(修订版).北京：北京师范出版社.

唐文清，方杰，蒋香梅，张敏强.(2014).追踪研究方法在国内心理研究中的应用述评.心理发展与教育，30(2)，216-224.

王孟成，毕向阳，叶浩生.(2014).增长混合模型：分析不同类别个体发展趋势.社会学研究，4，220-241.

巫锡炜.(2009).中国高龄老人残障发展轨迹的类型：群组发展建模的一个应用.人口研究，33(4)，54-67.

Armitage，C.J.，Rowe，R.，Arden，M.A.，& Harris，P.R.(2014).A brief psychological intervention that reduces adolescent alcohol consumption.JournalofConsulting&ClinicalPsychology，82(3)，546-550.

Eggleston，E.P.，Laub，J.H.，& Sampson，R.J.(2004).Methodological sensitivities to latent class analysis of long-term criminal trajectories.JournalofQuantitativeCriminology，20(1)，1-26.

Haviland，A.，Jones，B.，& Nagin，N.S.(2011).Group-Based Trajectory Modeling Extended to Account for Non-Random Subject Attrition.SociologicalMethods&Research，40(2)，367-390.

Haviland，A.，Nagin，D.S.，& Rosenbaum，P.R.(2007).Combining propensity score matching and group-based trajectory analysis in an observational study.PsychologicalMethods，12(3)，247-267.

Jones，B.L.，& Nagin，D.S.(2007).Advances in group-based trajectory modeling and an sas procedure for estimating them.SociologicalMethods&Research，35(4)，542-571.

Jones，B.L.，& Nagin，D.S.(2013).A note on a stata plugin for estimating group-based trajectory models.SociologicalMethods&Research，42(4)，608-613.

Lacourse，E.，Nagin，D.，Tremblay，R.E.，Vitaro，F.，& Claes，M.(2003).Developmental trajectories of boys’ delinquent group membership and facilitation of violent behaviors during adolescence.JournalofAdvancedNursing，15(1)，183-197.

Lee，C.M.，Neighbors，C.，Lewis，M.A.，Kaysen，D.，Mittmann，A.，Geisner，I.M.，& Larimer，M.E.(2014).Randomized controlled trial of a spring break intervention to reduce high-risk drinking.JournalofConsulting&ClinicalPsychology，82(2)，189-201.

Morgan，P.L.，Farkas，G.，& Wu，Q.(2011).Kindergarten children’s growth trajectories in reading and mathematics：Who falls increasingly behind?JournalofLearningDisabilities，44(5)，472-488.

Nagin，D.S.(1999).Analyzing developmental trajectories：A semiparametric，group-based approach.PsychologicalMethods，4(2)，139-157.

Nagin，D.S.(2005).Group-basedmodelingofdevelopment.Cambridge，MA：Harvard University Press.

Nagin，D.S.，& Land，K.C.(1993).Age，criminal careers，and population heterogeneity：Specification and estimation of nonparametric mixedpoisson model.Criminology，31(3)，327-362.

Nagin，D.S.，& Odgers，C.L.(2010).Group-based trajectory modeling in clinical research.AnnualReviewofClinicalPsychology，6(4)，109-138.

Nagin，D.S.，& Odgers，C.L.(2010).Group-based trajectory modeling(nearly)two decades later.JournalofQuantitativeCriminology，26(4)，445-453.

Nagin，D.S.，& Piquero，A.R.(2010).Using the Group-Based Trajectory Model to Study Crime Over the Life Course.JournalofCriminalJusticeEducation，21(2)，105-116.

Nagin，D.S.，& Tremblay，R.E.(2001).Analyzing developmental trajectories of distinct but related behaviors：A group-based method.PsychologicalMethods，6(1)，18-34.

Peer，J.E.，& Spaulding，W.D.(2007).Heterogeneity in recovery of psychosocial functioning during psychiatric rehabilitation：An exploratory study using latent growth mixture modeling.SchizophrRes，93，186-193.

Tremblay，R.E.，Nagin，D.S.，Séguin，J.R.，Zoccolillo，M.，Zelazo，P.D.，Boivin，M.，& Japel，C.(2004).Physical aggression during early childhood：Trajectories and predictors.TheCanadianChildandAdolescentPsychiatryReview，14(1)，3-9.

Ward，A.K.，Day，D.M.，Bevc，I.，Ye，S.，Rosenthal，J.S.，& Duchesne，T.(2010).Criminal trajectories and risk factors in a canadian sample of offenders.CriminalJustice&Behavior，37(11)，1278-1300.