基于批量订购的铁路集装箱货运多等级运价研究

张小强，张 琪，罗 涛，张蓉蓉*

(1.西南交通大学交通运输与物流学院，成都610031；2.广州铁路集团公司货运处，广州510088)

0 引言

集装箱运输在经济性和方便性方面的优势突出，是铁路降低运输成本、提高运作效率的有效方法之一.然而，相比于其他发达国家，我国铁路集装箱运输目前仍然处于落后阶段，仅占铁路总货运量的2%～3%.现行的铁路集装箱定价方法仍存在一定的不足，例如没有根据市场需求进行及时反应，而损失了部分货源，尤其是在铁路运价逐步放开的大环境下，原有的定价方法更加缺乏竞争力.为了提高铁路集装箱货运的竞争力，增大铁路的收益，寻求更为科学合理的定价方案是必要的.

动态定价作为企业提高收益能力的一种重要管理工具，在国内外航空运输、铁路客运领域的研究和应用已较为成熟.Levin[1]采用期权理论，假设售票公司向客户销售有期权的产品，并建立了离散时间的动态定价模型.李豪等[2]首先研究了两种相同易逝品在两个零售商竞争的环境下考虑客户策略行为的动态定价模型，并将模型拓展到考虑顾客分类和库存控制的情况.关于集装箱货运定价的研究，目前多数应用在海洋运输和多式联运当中，Rajkovic[3]建立了使海运集装箱运输成本和运输时间最小的多目标数学模型，并提供最佳的运输路线.刘迪等[4]从单起讫点着手，研究了随机需求下海铁联运的集装箱动态定价，建立对协议销售进行舱位控制的同时对自由销售进行动态定价的两阶段模型.

关于批量订购的研究，李根道等[5]分别提出了完全信息下，考虑需求学习的动态定价模型，并将模型拓展到考虑批量购买的情况.Zhang Xiaoqiang等[6]为了降低团体旅客的流失率从而提高列车的期望收益，建立了考虑团体旅客的高速铁路客运动态定价模型，并计算出使铁路收益最大的团体旅客最优折扣.这两篇文献是从易逝品销售及高铁客运角度研究的，目前研究集装箱批量订购的定价问题者较少.

综合当前研究的不足，本文针对铁路集装箱批量订购问题，建立了考虑批量订购的铁路集装箱动态定价模型.该模型能够优化客户订购不同数量舱位时的最优价格，使得铁路运营企业收益最大化.

1 构建模型

1.1 问题描述

(1)提前T时刻开始出售某趟货运列车的集装箱舱位，预售舱位数量为C，出售的舱位按标准TEU(Twenty-foot Equivalent Unit)集装箱.

(2)根据客户一次订购的集装箱舱位数将对应的订购价格划分成不同等级.

(3)客户需求到达，并以一定的概率订购j个舱位.

(4)客户在不同时间到达铁路系统并订购j个舱位的概率服从独立同分布.

(5)不考虑超订、退订的情况.

1.2 符号说明

j——客户订购的集装箱舱位数；

i——运价的等级，运价共分为I={1 ,2,…,n}等级；

Ji——i等级运价下的客户订舱数；

p——每个TEU舱位出售的基准价；

W——折扣集合其中每一个ωl代表一个折扣；

ωi——第i等级运价可以接受的折扣，且ωi∈W；

Pj——客户订购j个集装箱舱位的概率，服从泊松分布；

V(t,k)——t时刻，剩余舱位为k时铁路的期望收益.

1.3 建立模型

根据方程max[V(t-1,k-j)+pi'j,V(t-1,k)]确定铁路是否接受折扣集合中的各个折扣.当t=T时刻，表示铁路开始销售集装箱舱位，当t=0时刻，表示列车开行.该方程第1项表示在t-1时刻，铁路以价格pi'售出j个舱位的期望总收益，此时剩余舱位为k-j；第2项表示在t-1时刻，铁路未出售任何舱位的期望总收益，此时剩余舱位仍为k；只有当售出时的期望总收益大于未售出时的期望总收益时，决策者才愿意出售集装箱舱位.进而，客户愿意以价格pi'订购舱位的概率为F(pi')，则对应的期望收益为F(pi')max[V(t-1,k-j)+pi'j,V(t-1,k)]；而 不 愿意以价格pi'订购舱位的概率为1-F(pi')，则对应的期望收益为[1 -F(pi')]V(t-1,k).进而，客户订购j个舱位的期望收益为而客户未订购舱位的期望收益为P0V(t-1,k).为了实现铁路收益最大化，从所有满足以上条件的折扣中选择使得期望收益最大的折扣作为最优折扣进行销售.因此，铁路在t时刻，剩余舱位为k时的期望总收益可以表示为

其中，式(3)表示所有价格等级下客户订购集装箱舱位数集合构成了允许客户订购集装箱舱位数全集；式(4)表示任意两个等级的允许订购舱位数不重复.

参考Logit模型，给出了旅客的购买概率模型为

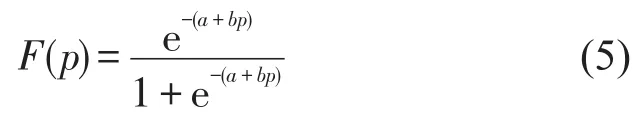
式中：参数b为正数，表示客户对于价格的敏感程度，当b越大时表示客户对价格越敏感；参数a=-p*b，其中p*可近似认为市场价格.

1.4 求解过程

Step 1设置，给一次性最多订购舱位数Z赋值.

证明

Step 2将舱位预售期分为T个时刻，在每一个时刻t下进行如下计算.

Step 3给k赋初始值，k=1.

Step 4t时刻客户可能订购的集装箱舱位数m=min(k,Z)，并根据该订购数量m确定运价等级i.

Step 5从l=1开始循环，

将折扣集合W中的第l个值ωl赋给ωi，即ωi←ωl，计算pi'=pωi.

根据价格pi'，按照式(1)计算期望收益V(t,k)，每次循环完执行l←l+1，直到l=L结束循环.

Step 6选择以上期望收益中最大的V(t,k)，并取对应的ωl作为本次优化的最优折扣.

Step 7执行k←k+1，并重复Step4～Step7，计算每个k情况下的最大的期望收益V(t,k)及最优折扣，直到k=K结束循环.

通过以上步骤，可求解动态定价下的最优折扣价格，使得铁路收益最大.

2 性能分析

2.1 最优解性质

当p满足关系式时，取得的p为最优价格.

可将该方程简化为

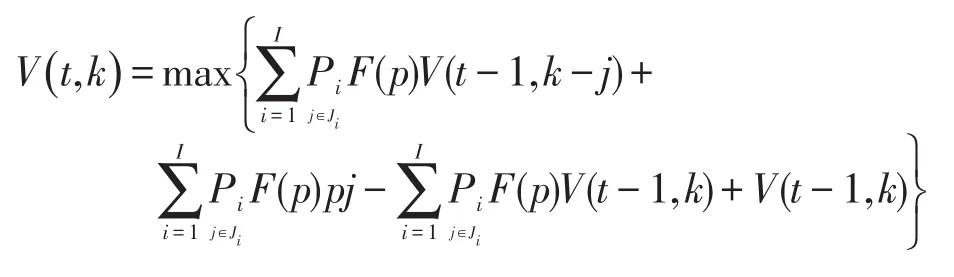
因此可将该问题转化为求方程的最大值问题.

对V(t,k)求二阶导数得

所以，当p满足关系式时，取得的p为最优价格，根据公式即可求出对应的最优折扣.

2.2 性能分析

性质1期望收益是a的减函数.

证明

对G(a)求一阶导数，得

∴G'(a)＜0恒成立

∴期望收益是a的减函数

因为a=-p*b，所以该性质也可以等价为期望收益是市场价格的增函数.

性质2当a+bp＞0时，期望收益V随着b的增大而减小；当a+bp=0时，期望收益V不变；当a+bp＜0时，期望收益V随着b的增大而增大.

证明

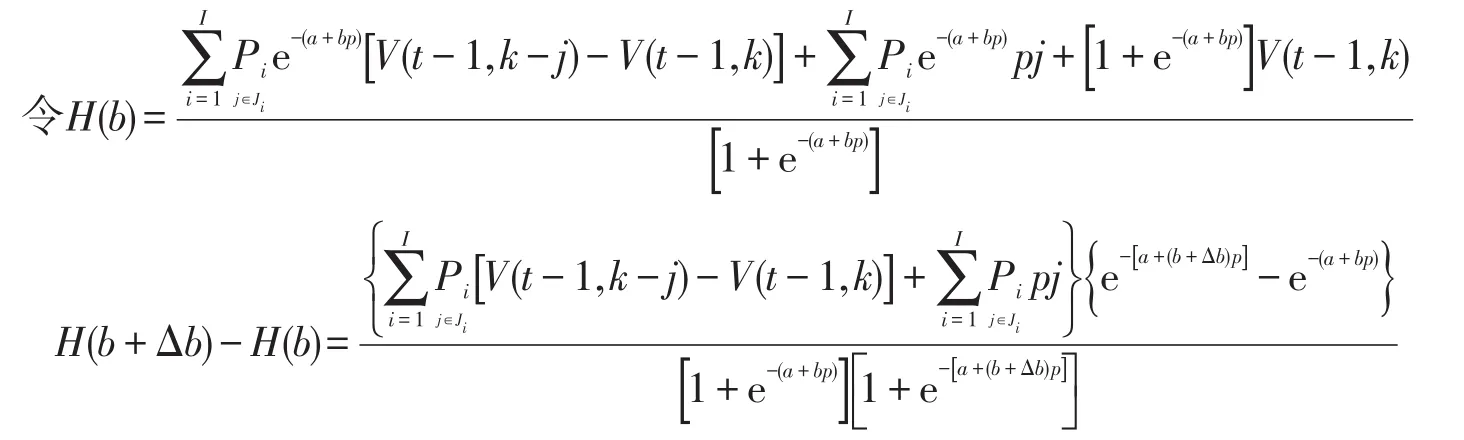
(1)当a+bp＞0时，e-(a+bp)为减函数.

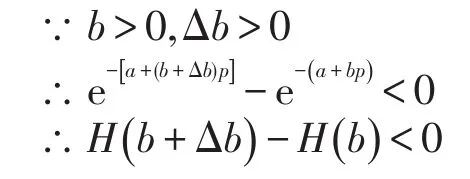
即期望收益V随着b的增大而减小.

(2)当a+bp=0时

即期望收益V不变.

(3)当a+bp＜0时，e-(a+bp)为增函数.

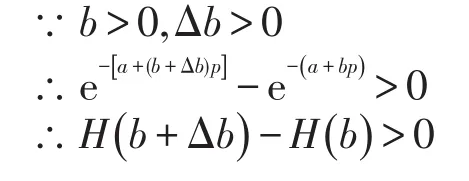
即期望收益V随着b的增大而增大.

通过最优解条件可以在已知市场价格和客户敏感性系数的情况下，对最优价格和期望收益进行估计，而根据性能分析的性质，可以在市场价格和客户敏感性变化时，对铁路可获得的期望收益进行估计，从而优化出最优价格.

3 算例分析

大朗到大红门的集装箱直达班列，满轴40辆车，每车可装2个TEU，即列车预售舱位数C为80TEU.以整车出售，每个集装箱舱位售价3万元.允许客户对集装箱舱位进行批量订购.为了对运价进行细分，铁路按照客户订购的集装箱舱位数，将运价分为不同的等级：将一次性订购1～10个集装箱舱位数对应的运价，分为10个价格等级，即一次性订购1个集装箱舱位对应的价格设为第1级价格，以此类推.由于客户一次性订购超过10个集装箱舱位的情况为小概率事件，因此本文未将其作为主要研究对象，并将一次性订购10个以上集装箱舱位情况下的价格按照一次性订购10个的价格进行优化.客户到达铁路并订购j个集装箱舱位的概率服从λ=1.5的泊松分布.客户订购集装箱舱位的购买概率分布函数的参数a、b的取值如表1所示.

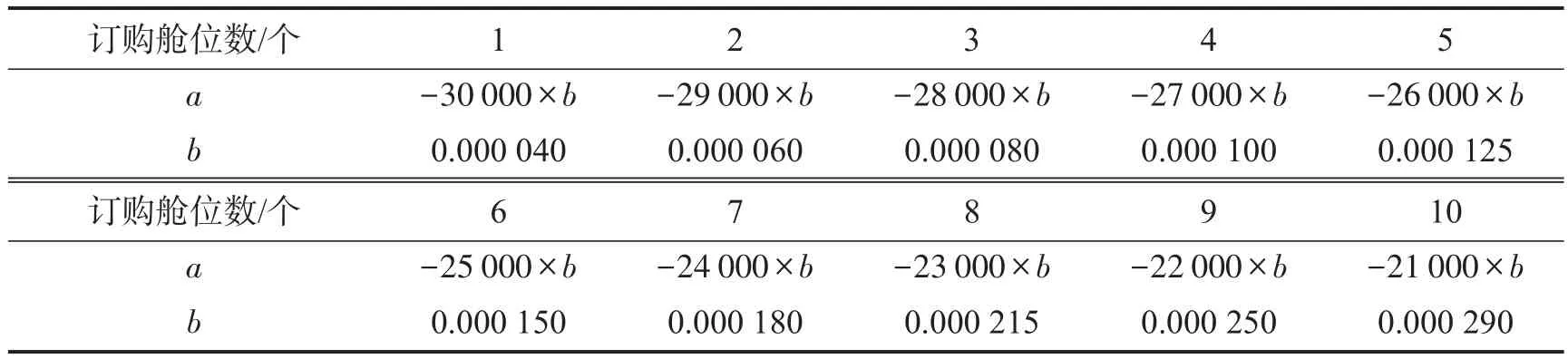
表1 购买概率的参数取值Table 1 The parameter of purchase probability

3.1 结果分析

通过动态定价模型，优化得出的在不同时刻订购不同数量的集装箱舱位时，使收益最大的最优折扣如图1所示.

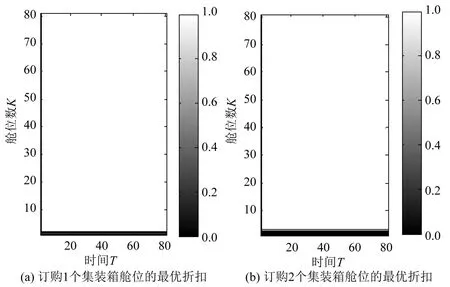
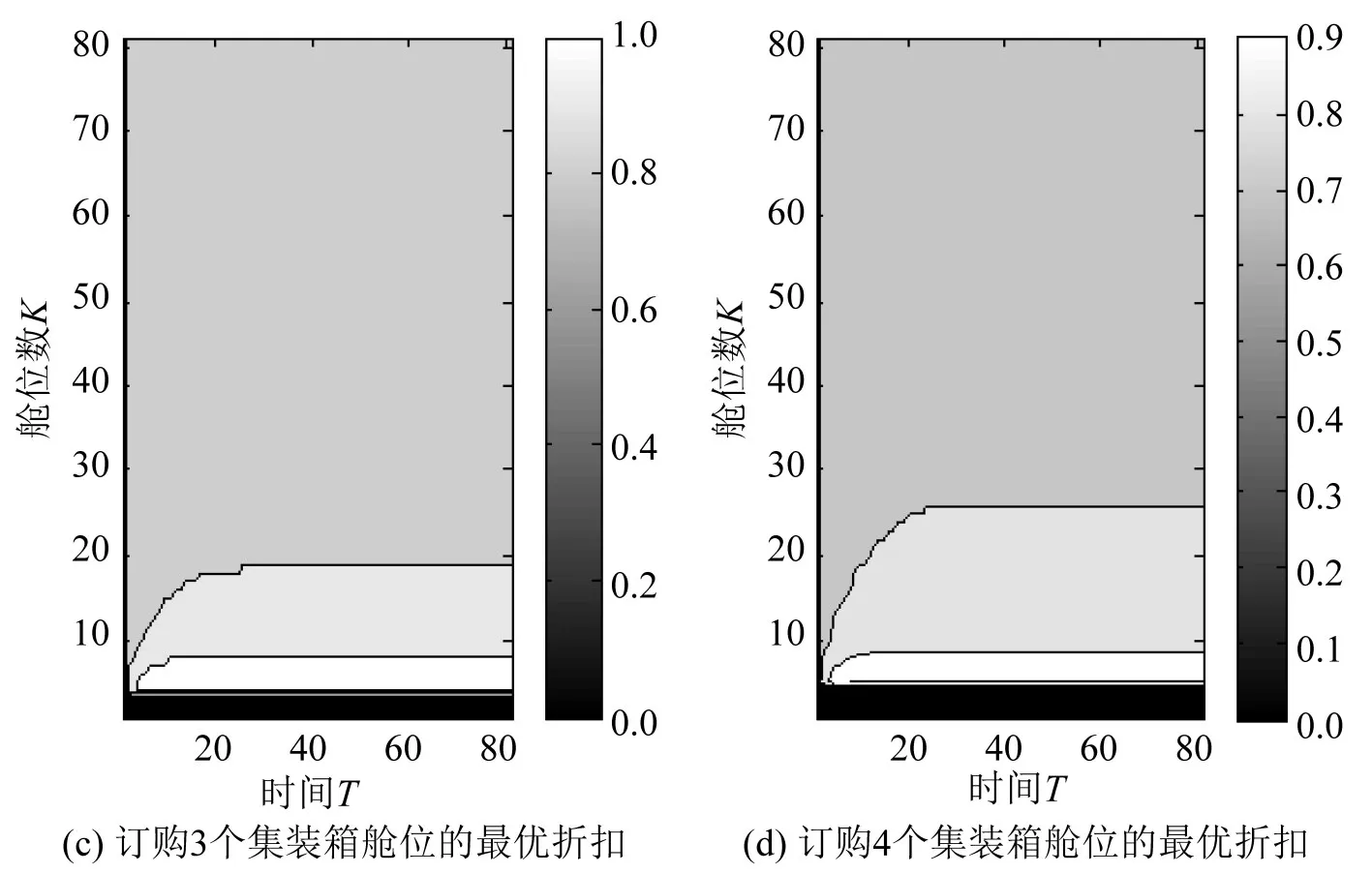
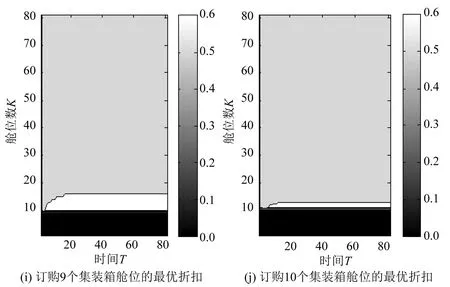
图1 订购集装箱舱位的最优折扣图Fig.1 Optimal discount of ordering containers

图1为等高线图，取图中的点及其灰度，并对比右侧色条，即可知该处对应的最优折扣.图中下部黑色区域表示未满足该等级价格下客户的订购需求时，未对其进行优化，即第10等级运价要求客户预定10个舱位，当舱位数k小于10时，不满足客户享受第10等级运价的订购要求，因此不对此种情况进行优化.从图中可知，当剩余时间相同时，剩余舱位越多，最优折扣越低；当剩余舱位数相同时，剩余时间越少，最优折扣越低.同时，对比10张图可以看出，单次订购的舱位数越多，能够享受的折扣越大.通过以上结果可知，在不同时刻订购不同数量的集装箱舱位时，能够计算出满足铁路收益最大的最优折扣价格，解决了铁路货运定价无法根据市场变化做出反应的问题.

客户需求到达铁路系统时，订购数量已确定.根据广铁集团实际的订购数据信息分析，需求到达服从λ=1.5的泊松分布.因此在这种情况下，铁路系统接收的是确定性需求，可将模型简化为

式中：V(i)表示第i个集装箱舱位订购需求到达时铁路的期望收益.

在该种情况下，假设所有订购数量的情况都存在，根据模型优化出的最优折扣如图2所示.

图2 模拟实际订购需求的最优折扣Fig.2 Optimal discount simulating the real order

根据优化结果可知，一次性订购的集装箱舱位数越多，能够享受的折扣越大.

根据订购需求到达服从的泊松分布，通过MATLAB模拟的客户需求为].由于本问题研究的是客户需求到达铁路系统并订购舱位的问题，而随机数中产生的0表示客户需求未到达铁路系统，因此将该种情况舍去.

按照购买概率进行求算，当按照全价向客户出售时，购买概率如表2所示.

表2 按照全价出售时的购买概率Table 2 Purchase probability according the whole price

按照表2的购买概率及随机模拟的订单需求，可获得的期望收益为1 109 600元.

根据模型可以求算出各个订单对应的最优折扣，如图3所示.

图3 模拟实际订购需求的最优折扣Fig.3 Optimal discount simulating the real order

通过模型求算可知，客户订购1、2个集装箱舱位时均不享受折扣优惠，客户订购3个集装箱舱位时享受8.8折优惠，客户订购4个集装箱舱位时享受7.9折优惠，客户订购5个集装箱舱位时享受6.4折优惠，在随机生成订单需求模拟实际订购情况下可获得的最大期望收益为1 158 700元.由此可知，采用该模型优化使得铁路的收益提高了4.24%.

3.2 性能分析

以第4等级运价为例，分别对该等级运价情况下，购买概率的参数a、b进行性能分析.

(1)确定参数a不变.

确定参数a=-27 000×b不变，通过变化参数b得到不同的期望收益和最优折扣，如图4所示.

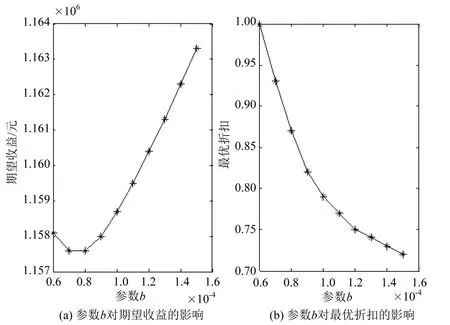
图4 参数b变化时期望收益及最优折扣变化图Fig.4 Expected revenue and optimal discount when parameterbchanging

根据图4可知，当确定参数a不变时，随着参数b的增加，反映出客户的敏感性不断提高，结果使最优折扣从1.00逐渐降低到0.72，并且其下降速度逐渐减慢.对期望收益而言，当满足a+bp=0时，p=270 000，介于价格27 900和26 100之间，对应b的取值在[0.000 07,0.000 08]之间，因此在此区域期望收益达到最低点，而在该区域左侧，满足a+bp＞0，期望收益不断减小，在该区域右侧，满足a+bp＜0，期望收益不断增加，均符合性质2.

在实际情况中，当客户对于价格的敏感性提高时，铁路可以通过适当降价来提高收益，客户的敏感性提高的越快，价格降低得应该越慢.

(2)确定参数b不变.

确定参数b=0.000 15不变，通过变化参数a得到不同的期望收益和最优折扣，如图5所示.

图5 参数a变化时期望收益及最优折扣变化图Fig.5 Expected revenue and optimal discount when parameterachanging

从图5可以看出，随着a的不断增大，期望收益和最优折扣都呈现比较均匀的减小，符合性质1.

由于a=-p*b，且b确定不变，因此该性质可以等效为，当市场价格不断减小时，期望收益不断减少.

在实际情况中，当市场价格减小的情况下，铁路应该适当降低价格，以达到该市场价格下的最大收益，同理，当市场价格提高的情况下，铁路应当适当提高价格，以达到该市场价格下的最大收益，并且价格的变化应该参考市场价格的变化而均匀浮动.

4 结论

本文针对批量订购集装箱舱位进行研究，按照客户一次性订购集装箱舱位的数量，将对应的运价进行等级细分.以大朗到大红门的集装箱班列为例，建立使得铁路集装箱货运期望收益最大的动态定价模型，能够求算出在不同时刻客户需求到达铁路并订购不同数量的集装箱舱位时，能够满足铁路期望收益最大的最优折扣，并按照客户订购j个舱位服从的概率分布随机生成一组确定性需求，当需求确定的情况下，为使铁路收益最大，对客户订购不同数量的集装箱舱位应采取的最优折扣价格.最后，通过性能分析得出市场变化情况下，铁路应采取的策略：一方面，当客户对于价格的敏感性提高时，铁路可以通过适当降价来提高收益，客户的敏感性提高的越快，价格降低得应该越慢；另一方面，当市场价格提高的情况下，铁路应当适当提高价格，反之亦然，并且价格的变化应该参考市场价格的变化而均匀浮动.

[1]LEVIN Y,MCGILL J,NEDIAK M.Price guarantees in dynamic pricing and revenue management[J].Operations Research,2007,55(1):75-97.

[2]李豪.竞争环境下考虑顾客行为的易逝品动态定价策略研究[D].重庆:重庆大学,2010.[LI H.Dynamic pricing strategy for perishable products in competitive markets with consumer behavior[D].Chongqing:Chongqing University,2010.]

[3]RAJKOVIC R,ZRNIC N,COKORILO O,et al.Multi-objective container transport optimization on intermodal networks based on mathematical model[C].Proceedings of the Second International Conference on Traffic and Transport Engineering(ICTTE),2014:26-35.

[4]刘迪,杨华龙.单起讫点间集装箱海铁联运动态定价模型[J].交通运输系统工程与信息,2012,12(4):122-127.[LIU D,YANG H L.Dynamic pricing model of container sea-rail intermodal transport on single OD line[J].Journal of Transportation Systems Engineering and Information Technology,2012,12(4):122-127.]

[5]李根道.模型不确定下的收益管理动态定价策略研究[D].重庆:重庆大学,2009.[LI G D.Dynamic pricing strategy for revenue management with model uncertainty[D].Chongqing:Chongqing University,2009.]

[6]ZHANG X Q,ZHANG Q,LI Q Q,el al.Dynamic pricing for passenger groups of high-speed rail transportation[J].Journal of Rail Transport Planning&Management.2017,6(4):346-356.