VSi2嵌锂性质的第一性原理

龙科成，李 智，丁 静，龙朝辉，李小波，尹付成



VSi2嵌锂性质的第一性原理

龙科成1, 2，李 智1, 2，丁 静3，龙朝辉1, 2，李小波1, 2，尹付成1, 2

(1. 湘潭大学 材料设计及制备技术湖南省重点实验室，湘潭 411105；2. 湘潭大学 材料科学与工程学院，湘潭 411105；3. 中南大学 冶金与环境学院，长沙 410083)

采用基于密度泛函理论的第一性原理计算Li嵌入VSi2的各种可能反应的嵌Li形成能、理论比容量和体积膨胀率，从热力学上证实VSi2可以与Li反应，并得到最有可能的反应路径为：Li嵌入VSi2中首先生成V5Si3和Li13Si4；然后Li13Si4与Li反应形成Li21Si5；V5Si3不再与Li反应；最终态为V5Si3和Li21Si5。通过对嵌Li路径的分析，得到Li-Si-V三元系0K相图。进一步计算VSi2和V5Si3的电子结构和弹性性质，发现嵌Li前后硅化物的导电性质没有改变，但嵌Li产物V5Si3的导电性和延展性优于基体VSi2。计算结果表明：VSi2在嵌Li过程中生成的V5Si3，可以作为缓解体积膨胀的缓冲相和具有更好导电性能的导电剂，从而提高其脱嵌Li的循环性能。

第一性原理；VSi2；嵌锂性质；相图；电子结构；弹性性质

随着社会的飞速发展，能源危机与环境问题日益凸显，全球能源的消耗正逐渐从传统化石能源转向其它清洁高效能源。高效清洁能源的存储是电动汽车和智能电网的关键技术，对新能源汽车等国家战略新兴产业的发展具有重要意义。锂离子电池是目前广泛应用的一种能源存储器件[1]。目前，商业化生产的锂离子电池负极材料普遍采用的是石墨类碳材料，但这类负极材料存在比容量低(理论比容量372 mA∙h/g)、易发生有机溶剂共嵌入等特点，更不能满足未来高比容量动力锂离子电池的需要[2−3]。因此，开发新型高比容量的锂离子电池负极材料已极具迫切性。Si因具有已知最高的比容量(4209.7 mA∙h/g)、低嵌脱Li电位(0.02~0.6 V(vs Li+/Li))、资源丰富以及环境友好等优点而备受瞩目[3−5]。但是纯Si在嵌Li过程中体积将会发生剧烈膨胀，这易导致电极容量急剧衰减、循环性能恶化。研究发现[6−7]，将Si与惰性嵌Li金属合金化或复合化可有效缓解Si基负极材料在嵌Li过程中产生的体积剧烈膨胀所引起的失效，从而提高其循环性能，如Si-Cr[8−9]、Si-Mo[9−11]、Si-Ni[12−13]、Si-Fe[12, 14]、Si-Zr[15]、Si-V[11]等。但在过渡金属硅化物是否与Li发生反应这个问题上存在争论。FLEISCHAUER等[7]在研究TM-Si/Si(TM=Fe,Mn,Cr,Ni)作为负极材料时，认为最终的容量全部由Si提供，所以过渡金属硅化物是非活性物质，只有Si是活性物质。而文献[11, 13]中报道，TM-Si(TM=Ni，Ti，V，Mo)基合金作为负极材料的最终嵌Li容量远大于单纯由Si所提供的容量，说明过渡金属硅化物也可成为活性物质。HWANG 等[11]研究发现Si0.58V0.42合金薄膜电极在嵌Li过程中形成的金属硅化物作为缓冲相，缓解了嵌Li过程中的体积膨胀效应，循环100次后的放电比容量衰减了15%。而纯Si薄膜电极循环100次后的放电比容量衰减了68%。所以，与纯Si薄膜电极相比，由于硅化物相的缓冲作用，Si0.58V0.42合金薄膜电极的循环性能提升了很多。但缓解体积膨胀效应的缓冲机制没有合理的解释，哪些V-Si化合物是活性物质也不确定。也就是说嵌Li反应机理还不是很清楚。因为嵌Li反应的具体过程，实验很难检测到。已有研究[16−17]表明，用第一性原理的方法可以计算锂离子电池电极材料的嵌Li性质，并可以与实验较好地符合。因此，有必要采用第一性原理计算来研究V-Si化合物中富Si相VSi2的嵌Li路径并阐明其嵌Li性质。本文作者采用基于密度泛函理论的第一性原理计算方法，计算并讨论了Li嵌入VSi2的各种可能的反应，从而推导出Li嵌入VSi2最有可能的反应路径，并分析了该路径下各个V-Si化合物的电子结构和弹性性质，预测了VSi2作为锂离子负极材料的嵌Li性能。这种计算模拟VSi2嵌Li过程的研究思路，可预测新材料的的嵌Li性能，对设计和研发新型锂离子电池负极材料具有重要的理论指导意义。

1 计算方法

本文作者采用基于密度泛函理论的第一性原理计算软件VASP(Vienna Ab-initio simulation package)[18−19]进行计算。离子和电子之间的相互作用采用全电子Blöchl投影缀加波函数(Projector augmented waves，PAW)[20]方法描述。交换关联势用广义梯度近似(GGA)下的Perdew-Burke-Emzerhof(PBE)泛函[21]进行处理。各原子的最外层电子组态分别为Li-1s22s1、Si-3s23p2和V-3d34s2。平面波截断能取400eV，以保证足够收敛。布里渊区的K点对于六角晶系按Monkhorst-Pack方法以Gamma点为中心自动产生，其他晶系采用Monkhorst-Pack特殊K点网络方法[22]。K点网络数目经过了优化测试，如VSi2的K点网络设置为13×13×9。在结构优化过程中，每个结构都进行了全优化，直到原子间的Hellmann-Feynman力小于0.01 eV/Å为止。

VASP计算的能量全部是在0 K下进行的，所以本研究中计算出的形成焓值也是在0 K的条件下模拟的，而各个化合物的形成焓的实验值都是在常温下测得的，因此，不能排除温度的差别所带来的影响，当然也不能排除理论算法的选择所带来的误差以及实验本身所产生的误差。本研究的计算值与实验值的误差在5%以内是可以接受的。有研究[23]表明：Li-Si化合物在0~300 K之间的自由能的变化不超过20 meV/atom。所以用第一性原理计算的方法来模拟实际的嵌Li过程是合理的。

嵌Li形成能(Δ)定义为

平均嵌Li电位可表示为[24]

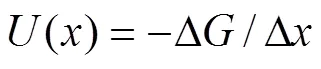
式中：吉布斯自由能Δ=ΔΔ−Δ；Δ为反应前后体系能量的变化(嵌Li形成能)；Δ为嵌Li量。Δ和Δ分别是反应前后的体积变化和熵值变化导致的吉布斯自由能变化项，通常Δ的数量级远大于Δ和Δ，因此，平均嵌Li电位可近似等于平均嵌Li形成能，即嵌Li形成能(Δ)除以嵌Li量(Δ)：

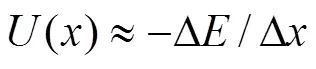
理论质量比容量cal定义为

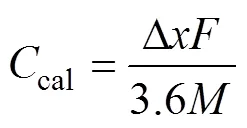
式中：Δ为单元晶胞的嵌Li量；为法拉第常数；为该电极材料的相对分子质量。

根据电极材料嵌Li前后的体积变化，定义体积膨胀率()为

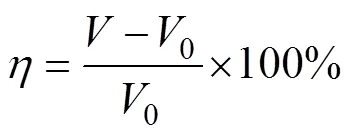
式中：为嵌Li后电极材料单元晶胞的体积；0为嵌Li前电极材料单元晶胞的体积。

在=0 K和=0 Pa下，原子几乎不振动，所以原子振动增加的能量可以不用考虑，此时，化合物的形成焓与化合物的形成能的计算值是等同的。比如V-Si二元化合物的单位原子的形成焓(Δf(VSi(1−)))可定义为

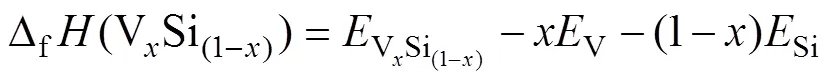
通过对晶体原胞施加一系列微小应变得到相对应的总能，可以求得弹性常数。对于六方晶系，有5个独立的弹性常数：11、12、13、33和44。就四方晶系而言，有6个独立的弹性常数：11、12、33、13、44和66。四方晶系和六方晶系的体积模量()、剪切模量()和泊松比()的详细计算步骤可参考文献[25−26]。

2 计算结果与讨论

2.1 Li-Si-V三元系中各个化合物的总能和形成焓

根据V-Li二元相图，Li与V之间未能形成化合物。根据LOZOVA等[27]的报道，Li-Si-V三元系没有出现新的三元化合物。所以，只考虑Li-Si和V-Si的化合物。利用最新的无机晶体结构数据库(Inorganic crystal structure database，ICSD)，首先计算了Li-Si二元系和V-Si二元系中各相的总能。为了保证计算的准确性，优化了各化合物的晶格常数，并与实验值对比，然后根据式(6)计算出所有化合物的形成焓，进一步与已报道的计算值或实验值对比，见表1。从表1中可以看出：Li-Si二元系和V-Si二元系中各相的晶格常

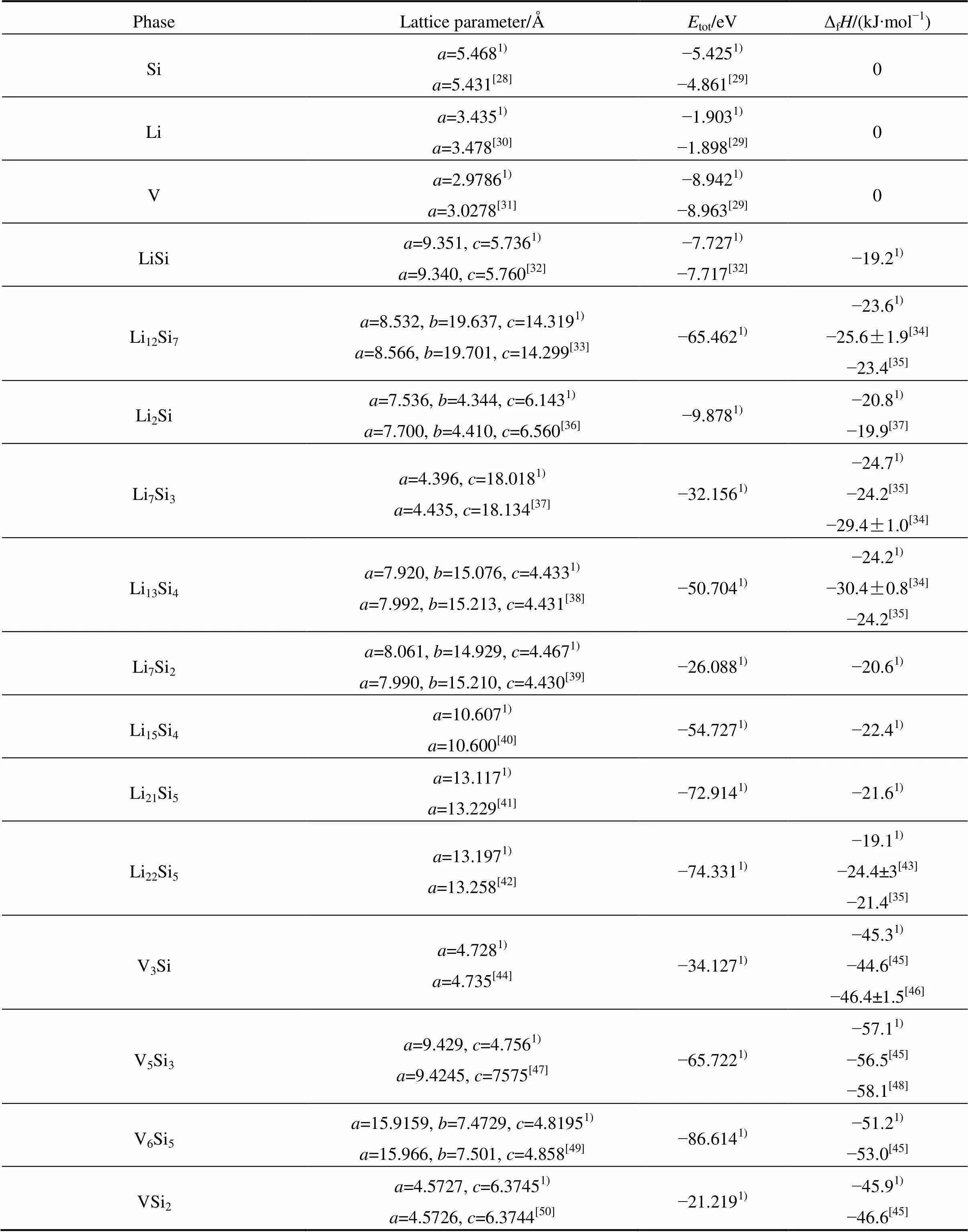
表1 Li-Si-V三元系各化合物的晶格常数、单位晶胞的总能和形成焓

1) Present work.

数的计算值与文献报道的实验值之间很接近，形成焓也与文献报告的计算值或实验值较为吻合。这为下一步计算反应式的反应形成能、体积膨胀率提供了可靠的保证。但并不是所有的化合物都稳定存在，因此，有必要对V-Si二元系和Li-Si二元系中各相的稳定性进行研究，筛选出最稳定的化合物，从而得到稳定的嵌Li反应。通过以上计算得到每个化合物的形成焓，由此获得Li-Si和Si-V各化合物的形成焓与成分的关系曲线，如图1所示。根据热力学分析，曲线的上方是不稳定的化合物。接下来的计算，只考虑最稳定的化合物。

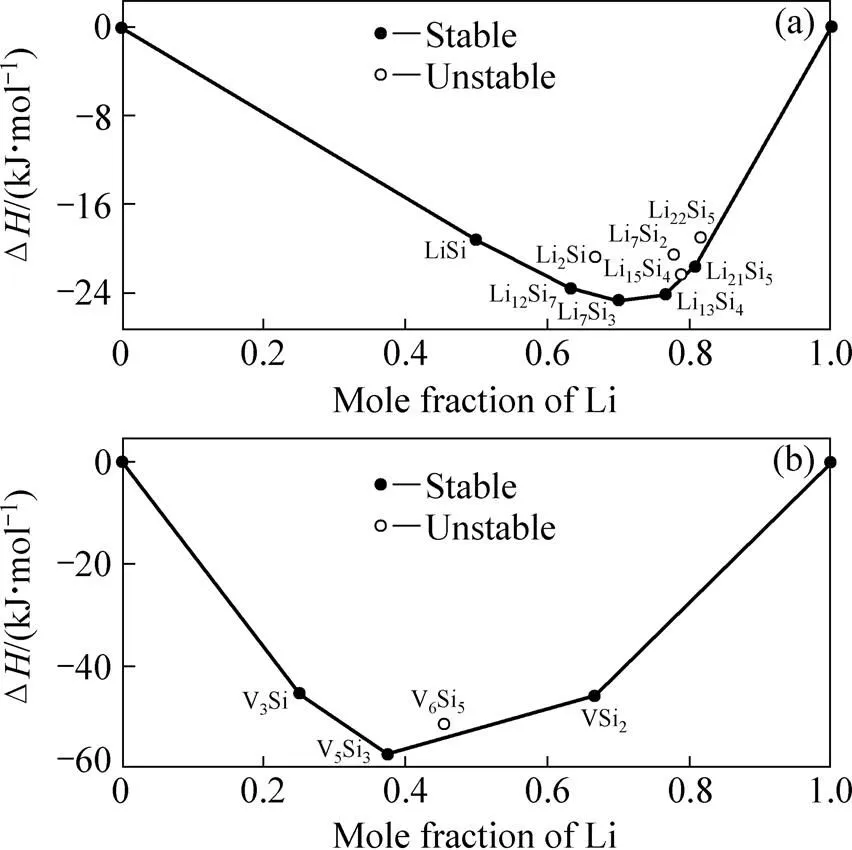
图1 Li-Si和V-Si二元系中各化合物的形成焓与成分的关系曲线

2.2 VSi2的嵌Li路径和计算的0 K相图

从热力学方面考虑，如果一个反应的形成能(反应物的总能减去生成物的总能)大于0，那么这个反应是可以自发进行的，且形成能越大，反应越容易发生。Li嵌入VSi2优先发生的那个反应，必然是平均嵌Li形成能最大的那个反应。为了筛选出最可能发生的反应，得到最有可能的反应路径，可把平均嵌Li形成能的大小作为判断反应发生先后的判据。当Li嵌入VSi2化合物中，Si是活性元素，能与Li反应形成Li-Si化合物，而V不与Li反应。Li与VSi2反应，会生成Li-Si化合物和Si含量更低的V-Si化合物或直接生成单质V。为了研究Li与VSi2的反应路径，本文作者根据式(1)~(3)计算了Li与VSi2反应生成V5Si3或V3Si或V的各种可能反应的平均嵌Li形成能，并分析最有可能的反应路径。

表2、3和4所列为Li与VSi2反应生成LiSi和V5Si3、V3Si、单质V的平均嵌Li形成能ΔΔ。从表2、3和4可以看出，各个嵌Li反应的嵌Li形成能大部分为正，说明VSi2是活性物质，可以与Li发生电化学反应。与表2相比，表3和4中各反应的平均嵌Li形成能明显较小，其中还有几个反应的平均嵌Li形成能为负。根据以上所述判据，说明Li刚开始嵌入VSi2时，VSi2最先变为V5Si3。再比较表2的各个反应，反应4的平均嵌Li形成能是最大的。因此，Li与VSi2反应首先生成V5Si3和Li13Si4。

在随后的嵌Li过程中，Li继续与V5Si3和Li13Si4反应。但是Li与V5Si3和Li13Si4中哪一个相先反应，有必要对Li-Si二元系的嵌Li路径进行讨论。根据前述，得出了Li嵌入Si的反应路径结果如下所示。

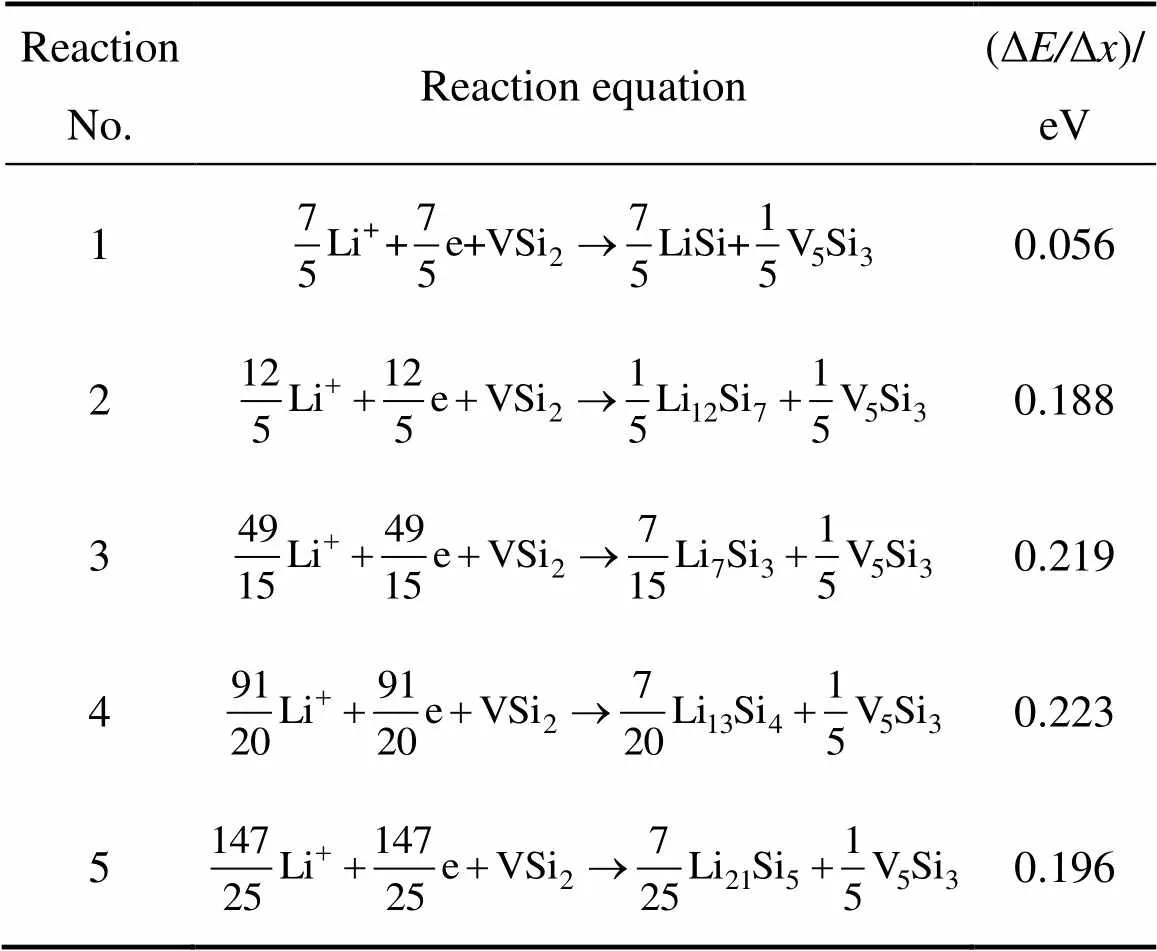
表2 Li++e+VSi2→LixSiy+V5Si3的平均嵌Li形成能(ΔE/Δx)

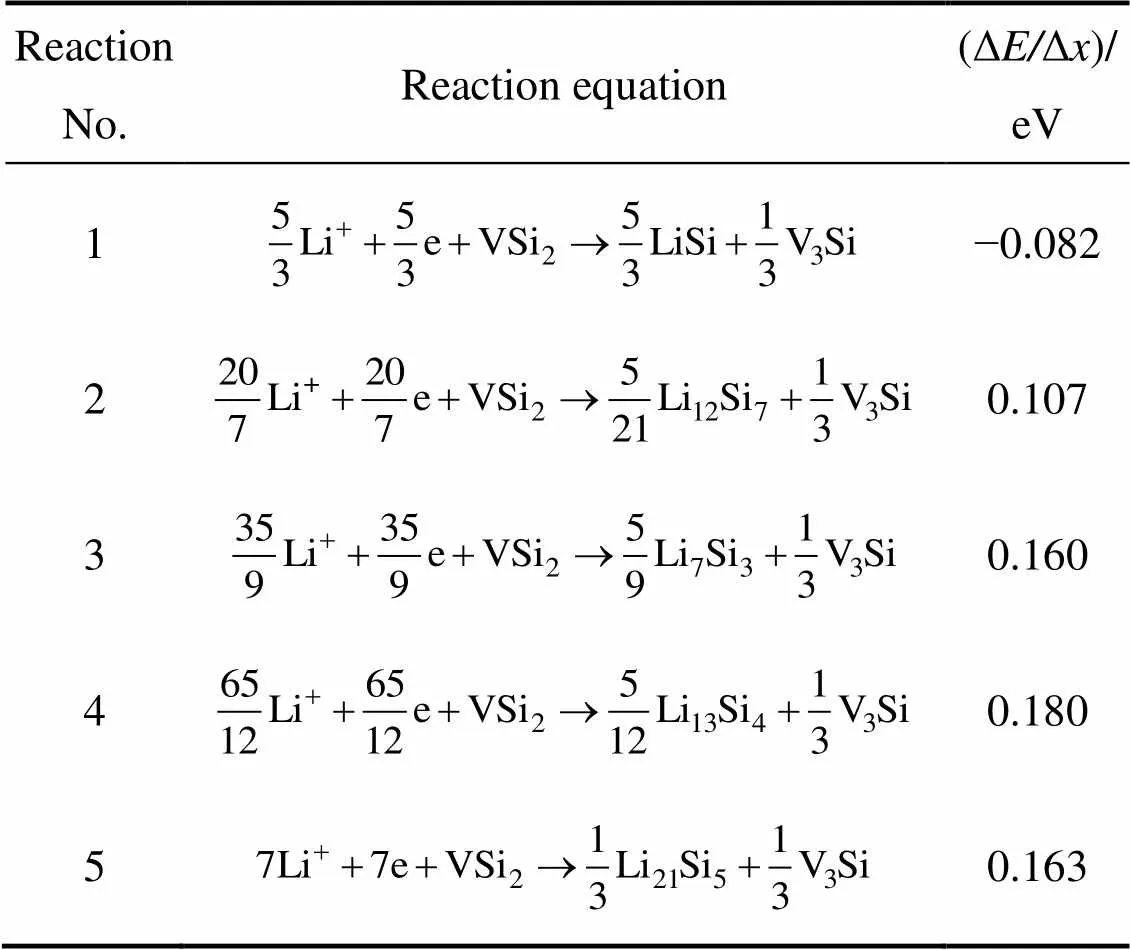
表3 Li++e+VSi2→LixSiy+V3Si的平均嵌Li形成能(ΔE/Δx)

表4 Li++e+VSi2→LixSiy+V的平均嵌Li形成能(ΔE/Δx)

Li嵌入Si的反应路径为

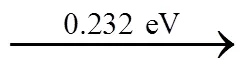
式(7)中箭头上的数值分别表示计算出的每一步的平均嵌Li形成能。该反应路径分为5步：Li嵌入Si中，首先形成LiSi；然后Li嵌入LiSi形成Li12Si7；Li继续嵌入Li12Si7形成Li7Si3；Li进一步嵌入Li7Si3形成Li13Si4；Li继续嵌入Li13Si4最终形成Li21Si5。

进一步计算Li与V5Si3生成V3Si和Li-Si化合物以及生成单质V和Li-Si化合物的平均嵌Li形成能Δ，其具体结果分别如表5和6所示。

表5和6中各反应的平均嵌Li形成能都为负值，说明Li不会再与V5Si3反应，即V5Si3为非活性物质。通过Li与Si的反应路径可以看出，在继续嵌Li的过程中，Li会与Li13Si4反应最终形成Li21Si5。综上所述可知，通过计算和分析可以得出Li嵌入VSi2最有可能的反应路径如下：

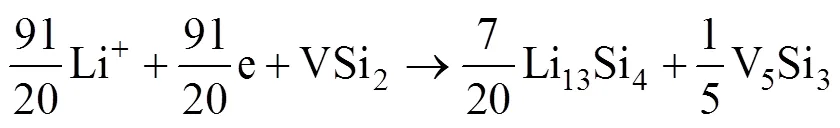
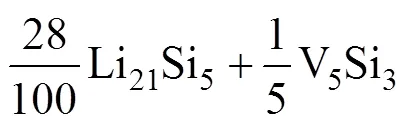
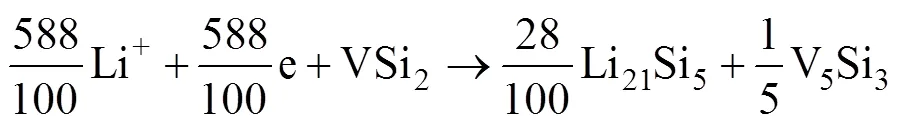
反应式(8)为第一步反应，反应式(9)为第二步反应，反式(10)为总反应。

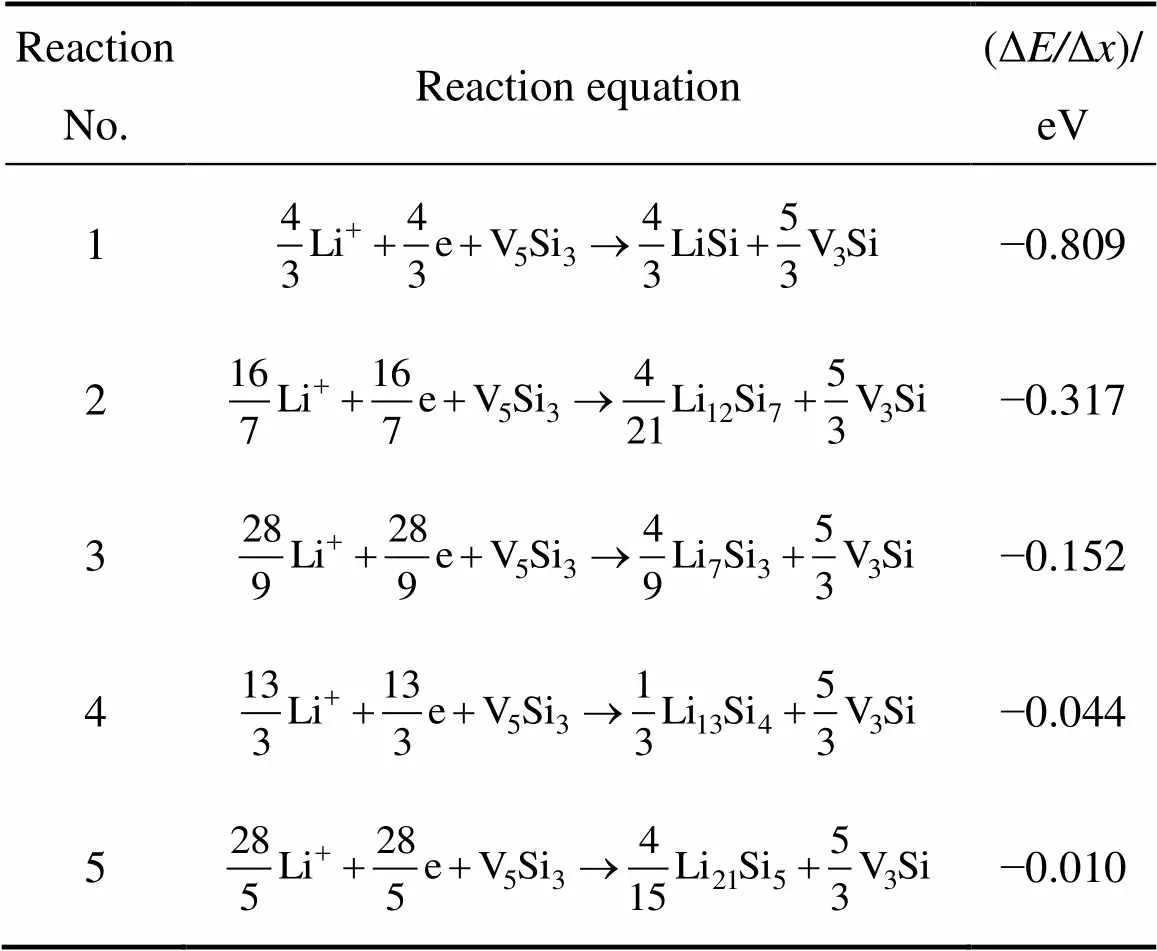
表5 Li++e+V5Si3→LixSiy+V3Si的平均嵌Li形成能(ΔE/Δx)

表6 Li++e+V5Si3→LixSiy+V的平均嵌Li形成能(ΔE/Δx)

由于三元等温截面中的每个相区都是热力学上最稳定的，也就是说，每个相区的相组成法则是，组成这个相区的所有相的总能必须是最低的。而以上述分析判断VSi2的嵌Li路径的方法正是寻找能量最低的反应物。所以相图上VSi2与Li之间的连线，所穿过的各相区，都是能量最低相区，这条连线就相当于VSi2的嵌Li路径。这也正是文献[51]所指出的，三元相图的每个三相区，对应于一个嵌Li反应。由此计算出的V-Si-Li在0 K时的等温截面如图2所示。这和Materials Project网站上提供的Li-Si-V三元系0 K相图符合。这为计算相图提供了一种新的思路。

2.3 VSi2嵌Li前后V-Si化合物的电子结构

图3所示为VSi2和V5Si3的总态密度和分波态密度。分析VSi2的态密度图(见图3(a))可知，在费米能级以下−14~−5 eV的态密度主要是Si(3s)提供，其次是Si(3p)电子的贡献，在−5至0 eV之间的态密度主要是V(3d)电子的贡献；在费米能级以上的态密度主要由V(3d)电子贡献，其他电子的贡献相对较少。此外，在−4.5 eV和1 eV附近，V的电子轨道和Si的电子轨道发生杂化。分析V5Si3的态密度图(见图3(b))可知，在费米能级以下−12~−5.8 eV之间V的电子和Si的电子提供的态密度相当，而Si(3s)电子的贡献稍多，在−5.8 eV以上的态密度则主要由V(3d)电子提供。此外在−7.3至−5.8 eV之间，V的电子轨道和Si的电子轨道发生杂化。图3(a)和(b)中显示的VSi2和V5Si3在费米能级处的态密度(F)都不为0，说明V5Si3和VSi2呈金属性质，这和能带结构的结果自洽。比较VSi2和V5Si3的总态密度图，VSi2费米能级两侧的尖峰相距较宽，即赝能隙较宽，说明VSi2的共价键较强。还可以看出，VSi2的(F)≈2.88 states/eV，V5Si3的(F)≈9.16 states/eV，这表明V5Si3的电子共有化运动较强，随着嵌Li量的增加，V—Si原子间的成键电子减少，提供导电电子增多，材料导电性增强。这说明嵌Li之后的V5Si3不仅起到抑制体积膨胀效应的缓冲相，还可以作为导电剂分布在基体中。

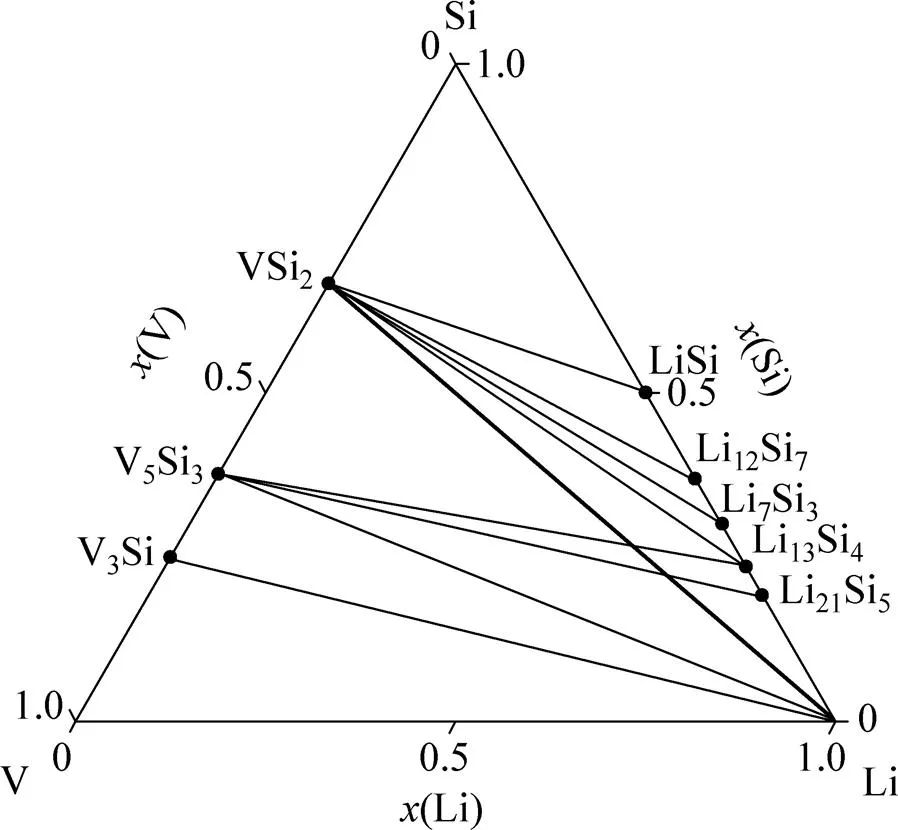
图2 Li-Si-V在0 K时的计算相图

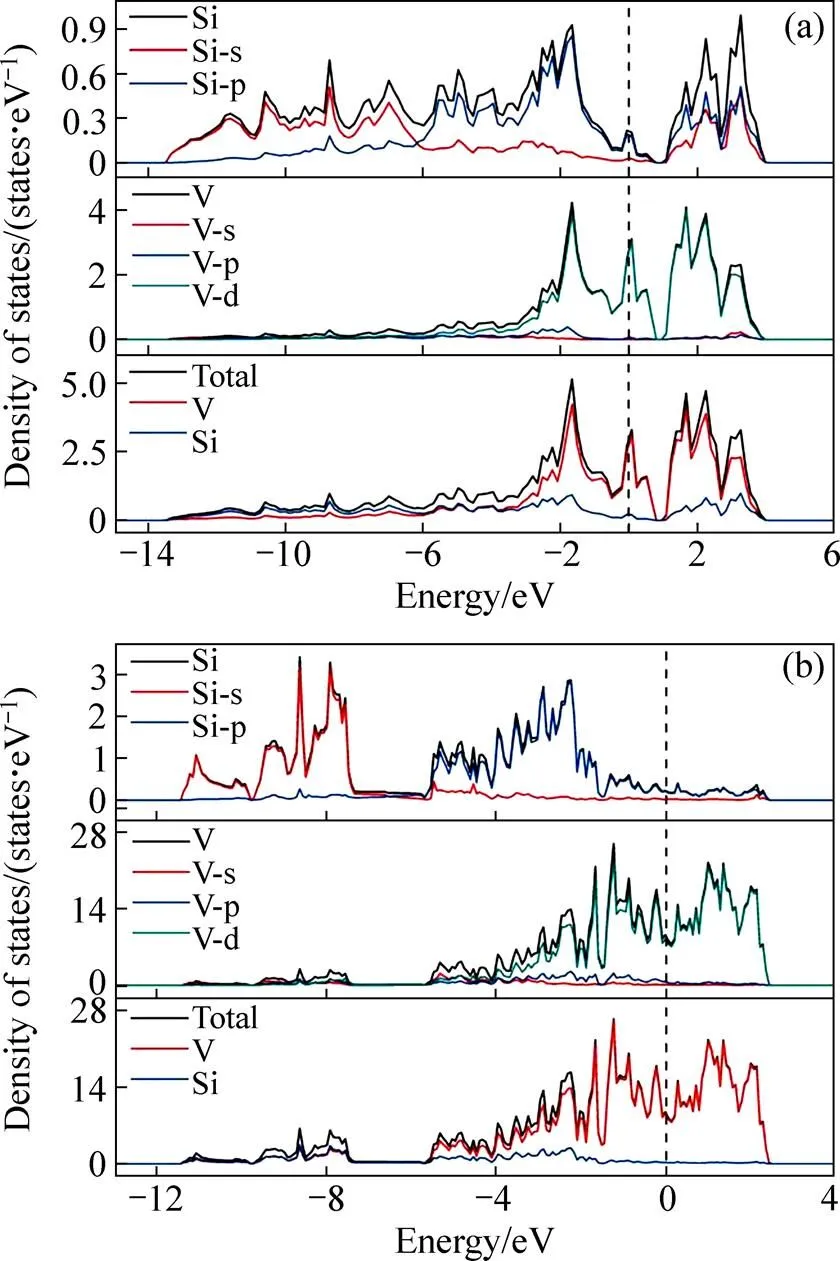
图3 嵌Li前后V-Si化合物的电子态密度图

2.4 VSi2嵌Li前后V-Si化合物的弹性性质

锂离子电池负极材料Si在嵌Li时体积膨胀，导致电极开裂和粉化，使循环性能变差。研究表明，采用Si与过渡金属复合生成的硅化物作为缓冲相能够有效地缓解体积膨胀效应。缓冲相的延展性优于基体时，抑制体积膨胀效应的作用越大。因此，有必要计算VSi2和V5Si3的弹性性质。本文作者采用第一性原理的方法计算VSi2和V5Si3的弹性常数以及根据Voigt-Reuss-Hill经验公式和泊松比公式[25−26]计算得到的体积模量()、剪切模量()和泊松比()，如表7所示。

表7 VSi2和V5Si3的弹性常数、体积模量(B)、剪切模量(G)、泊松比(μ)

V5Si3的弹性常数计算结果与文献[52]的计算值很接近。在判断一个相的弹性性质之前，首先要考虑该相在基态下是否满足力学稳定性的条件。根据四方晶系力学稳定性的判据[53]：

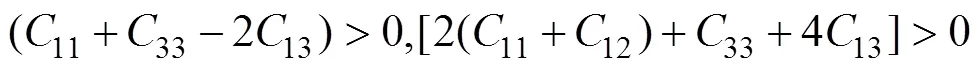
以及六方晶系力学稳定性的判据[54]：

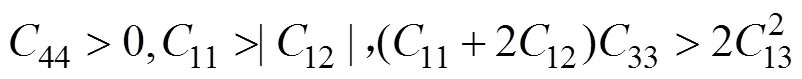
VSi2(Cr2Si-type)为六方晶系，V5Si3(W5Si3-type)为四方晶系，根据计算结果都满足力学稳定性的判定标准，所以这两种化合物结构稳定存在。

常用来预测材料的延展性和脆性[54]，/值越大，材料的延展性越好，反之，材料的脆性越大。的临界值为1.75。值大于1.75时为韧性材料，/值小于1.75时为脆性材料。此外，根据泊松比()也可以判断材料的韧性和脆性，泊松比()越大，材料的韧性越好。由表7可以得出，V5Si3和VSi2都为脆性材料，但V5Si3的泊松比()和值都大于VSi2，且V5Si3的/值非常接近临界值。这说明V5Si3的延展性和韧性大于VSi2的。这说明，VSi2经嵌Li后形成延展性更好的V5Si3能作为缓冲相，从而可以较好地抑制体积膨胀效应。

2.5 VSi2作为锂离子负极材料的嵌Li性能预测

根据式(1)~(5)计算VSi2嵌Li过程和总反应的平均嵌Li形成能(Δ/Δ)、嵌Li电压()、比容量(cal)和体积膨胀率()，如表8所列。

锂离子电池负极材料的嵌Li电压过小，嵌Li电压平台接近Li的析出电压，容易导致形成Li的树枝晶，电池的安全系数下降；而嵌Li电压过大，会对电池电压有负面影响，比如会降低电池的能量密度。新型的负极材料的比容量一定要大于石墨的理论比容量，但比容量与体积膨胀率成正比。KIRKLIN等[51]指出新型的锂离子负极材料最适当的性能参数为：嵌Li电压()为0.25~0.75 V；比容量(Cal)为372~1200 mA∙h/g。

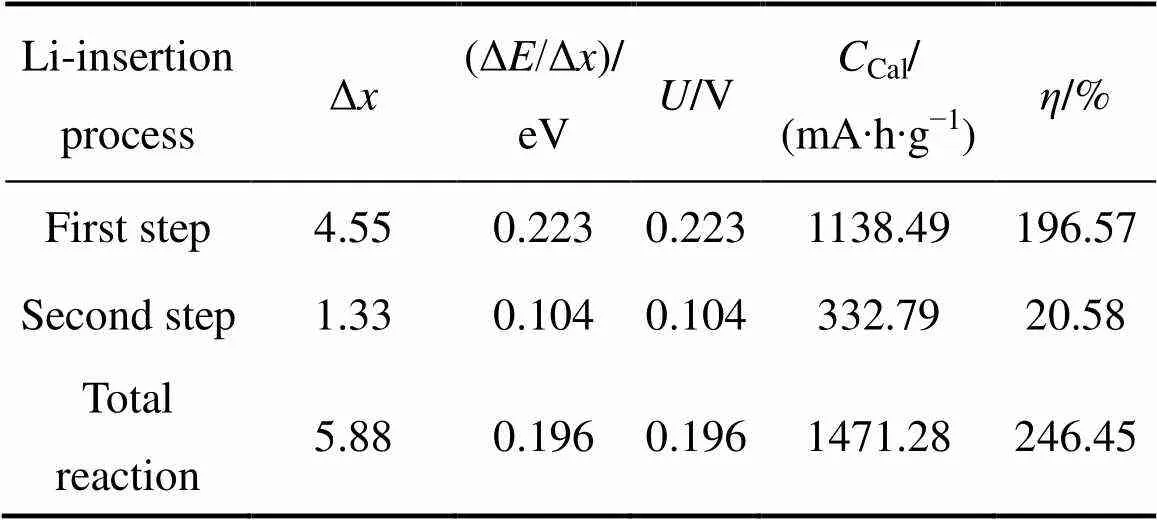
表8 VSi2嵌Li过程中的嵌Li量(Δx)、ΔE/Δx、U、CCal 和η

结合表8可知，VSi2作为锂离子负极材料，理论比容量为1471.28 mA∙h/g，小于文献[11]中Si0.58V0.42合金薄膜电极的比容量(Cal=1750 mA∙h/g)，这是由于合金Si0.58V0.42有多余的Si作为活性物质。VSi2的理论比容量远大于石墨的理论比容量(Cal=372 mA∙h/g)，体积膨胀率偏大，但小于Si负极体积膨胀率(Si≥300 %)。VSi2的嵌Li电压非常接近0.25 V，大于传统的石墨负极材料(≈0.1 V)，在充电时不易引起表面Li沉积的现象，其安全性能优于石墨负极材料的。此外，从表8中可以看出，刚开始嵌Li时，嵌Li电位较大，意味着容易嵌Li，这有利于锂离子电池的充电过程，随后嵌Li快达到饱和时，嵌Li电位较小，有利于锂离子的脱嵌过程。VSi2呈现金属导电特性，导电性优于半导体Si，且在嵌Li过程中，并未改变其本身的导电性质，而是会形成导电性和延展性更好的V5Si3。最终形成的硅化物V5Si3既缓解了体积膨胀，起到了缓冲相的作用，又提供了更好的导电性能，这在一定程度上缓解了体积膨胀率偏大带来的负面影响。综上所述可知，VSi2是一种有潜力的高比容量动力锂离子电池负极材料。

3 结论

2) V5Si3和VSi2都呈导体性质，且V5Si3的导电性比VSi2好，说明随着嵌Li量的增加，V—Si原子间的成键电子减少，提供导电电子增多，材料导电性增强。

3) V5Si3和VSi2都是脆性材料，但V5Si3的延展性较好。说明随着嵌Li进行，会生成延展性优于基体材料的缓冲相，从而缓解体积膨胀效应。

4) 通过对VSi2的嵌Li路径的分析，得到了Li-Si-V三元系0K相图，可为实验相图的测试提供参考。

[1] YANG Z, ZHANG W, SHEN Yue, YUAN Li-xia, HUANG Yun-hui. Next-generation energy storage technologies and their key electrode materials[J]. Acta Phys Chim Sin, 2016, 32(5): 1062−1071.

[2] LIANG Pu, ZHANG Lin-ping, WANG Fei, SUN Zhan-bo, HU Qing, YANG Sen, WANG Li-qun, SONG Xiao-ping. Effects of Cr content on electrochemical properties of melt-spun Al75−xSi25Cralloy anodes for lithium-ion batteries[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(6): 1393−1400.

[3] 苏明如, 王志兴, 郭华军, 李新海, 黄思林, 甘 雷. 粘结剂对锂离子电池 Si/C 复合材料性能的影响[J]. 中国有色金属学报, 2013, 23(4): 1059−1064. SU Ming-ru, WANG Zhi-xing, GUO Hua-jun, LI Xin-hai, HUANG Si-lin, GAN Lei. Effect of binders on performances of Si/C composites for Li-ion batteries[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(4): 1059−1064.

[4] 于志辉, 刘丹丹, 寇艳娜. 锂离子电池负极材料多孔硅/硅铁合金的制备及性能[J]. 北京工业大学学报, 2017, 43(2): 278−284.YU Zhi-hui, LIU Dan-dan, KOU Yan-na. Preparation and properties of Si/Si-Fe alloy porous composite as anode material in Li-ion battery[J]. Journal of Beijing University of Technology, 2017, 43(2): 278−284.

[5] TAO Hua-chao, FAN Li-zhen, QU Xuan-hui. Facile synthesis of ordered porous Si@C nanorods as anode materials for Li-ion batteries[J]. Electrochim Acta, 2012, 71(1): 194−200.

[6] 潘 璇, 王存国, 朱孟康, 刘艺涵, 路乃群. 锂离子电池大容量硅基负极材料的研究进展[J]. 化工科技, 2017, 25(1): 67−72.PAN Xuan, WANG Cun-guo, ZHU Meng-kang, LIU Yi-han, LU Nai-qun. Progress of silicon based negative electrode materials with high capacity for lithium ion batteries[J]. Science and Technology in Chemical Industry, 2017, 25(1): 67−72.

[7] FLEISCHAUER M D, TOPPLE J M, DAHN J R. Combinatorial investigations of Si-M (M=Cr+Ni, Fe, Mn) thin film negative electrode materials[J]. Electrochemical and Solid-State Letters, 2005, 8(2): 137−140.

[8] Weydanz W J, Wohlfahrt-Mehrens M, Huggins R A. A room temperature study of the binary lithium-silicon and the ternary lithium-chromium-silicon system for use in rechargeable lithium batteries[J]. J Power Sources, 1999, 81: 237−242.

[9] Courtel F M, Duguay D, Abu-Lebdeh Y, DAVIDSON I J. Investigation of CrSi2and MoSi2as anode materials for lithium-ion batteries[J]. J Power Sources, 2012, 202: 269−275.

[10] Hwang C M, Lim C H, Yang J H, PARK J W. Electrochemical properties of negative SiMoelectrodes deposited on a roughened substrate for rechargeable lithium batteries[J]. J Power Sources, 2009, 194(2): 1061−1067.

[11] Hwang C M, Park J W. Investigation of Si–M (M = Mo, Ti, or V) negative electrodes fabricated using RF/DC magnetron sputtering for lithium ion batteries[J]. Surface & Coatings Technology, 2010, 205(7): S439−S446.

[12] Wang Guo-xi, Sun Li, Bradhurst D H, ZHONG S X, DOU S X, LIU H K. Innovative nanosize lithium storage alloys with silica as active centre[J]. J Power Sources, 2000, 88: 278−281.

[13] Wang Z, Tian W H, Liu X H, LI Y, LI X G. Nanosized Si–Ni alloys anode prepared by hydrogen plasma-metal reaction for secondary lithium batteries[J]. Materials Chemistry & Physics, 2006, 100(1): 92−97.

[14] 杨 娟, 唐晶晶, 娄世菊, 邹幽兰, 周向阳. 锂离子电池用Si-Fe复合电极材料的制备及其性能[J]. 中南大学学报(自然科学版), 2011, 42(4): 859−864. YANG Juan, TANG Jing-jing, LOU Shi-ju, ZOU You-lan, ZHOU Xiang-yang. Preparation and performance of Si-Fe composite materials for lithium ion batteries[J]. Journal of Central South University (Natural Science Edition), 2011, 42(4): 859−864.

[15] Lee S J, Lee H Y, Baik H K, LEE S M. Si-Zr alloy thin-film anodes for microbatteries[J]. J Power Sources, 2003, 119: 113−116.

[16] Aydinol M K, Kohan A F, Ceder G, CHO K, JOANNOPOULOS J. Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides[J]. Physical Review B, 1997, 56(3): 1353−1365.

[17] 汝 强, 赵灵智, 田 琴, 胡社军. Sb薄膜嵌脱Li性质的平面波赝势法计算与实验研究[J]. 稀有金属材料与工程, 2011(s2): 70−74. RU Qiang, ZHAO Ling-zhi, TIAN Qin, HU She-jun. Investigation of lithium intercalation/extraction mechanism based on plane-wave pseudo-potential calculation and experimental method for Sb thin film[J]. Rare Metal Materials and Engineering, 2011(s2): 70−74.

[18] Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J]. Comp Mater Sci, 1996, 6(1): 15−50.

[19] Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Phys Rev B, 1996, 54(16): 11169−11186.

[20] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Phys Rev B, 1999, 59(3): 1758−1775.

[21] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Phys Rev Lett, 1996, 77(18): 3865−3868.

[22] Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations[J]. Phys Rev B, 1976, 13(12): 5188−5192.

[23] Chevrier V L, Zwanziger J W, Dahn J R. First principles study of Li-Si crystalline phases: Charge transfer, electronic structure, and lattice vibrations[J]. Journal of Alloys & Compounds, 2010, 496(1/2): 25−36.

[24] COURTNEY I A, TSE J S, MAO O, HAFNER J, DAHN J R. Ab initio calculation of the lithium-tin voltage profile[J]. Physical Review B, 1998, 58(23): 15583−15588.

[25] Panda K B, Chandran K S R. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory[J]. Computational Materials Science, 2006, 35(2): 134−150.

[26] Tao X, Jund P, Colinet C, TEDENAC J C. Phase stability and physical properties of Ta5Si3compounds from first-principles calculations[J]. Physical Review B, 2009, 80(10): 104103.

[27] Lozova O. Isothermal sections of phase diagrams for Li-V-{Ge, Si} systems at 570 K[J]. Ukrainskij Chemical Journal, 2001, 67(5): 27−29. (in Ukrainian)

[28] TÖBBENS D M, STÜßER N, KNORR K, MAYER H M, LAMPERT G. E9: The new high-resolution neutron powder diffractometer at the Berlin neutron scattering center[J]. Materials Science Forum, 2001, 378: 288−293.

[29] Wang Y, Curtarolo S, Jiang C, ARROYAVE R, WANG T, CEDER G, CHEN L Q, LIU Z K. Ab initio lattice stability in comparison with CALPHAD lattice stability[J]. Calphad, 2004, 28(1): 79−90.

[30] Berliner R, Fajen O, Smith H G, HITTERMAN R L. Neutron powder-diffraction studies of lithium, sodium, and potassium metal[J]. Physical Review B, 1989, 40(18): 12086−12097.

[31] Karen P, Suard E, Fauth F. Crystal structure of stoichiometric YBa2Fe3O8[J]. Inorganic Chemistry, 2005, 44(23): 8170−8172.

[32] KubotaY,Escano MCS, Nakanishi H, KASAI H. Electronic structure of LiSi[J]. Journal of Alloys and Compounds, 2008, 458(1): 151−157.

[33] NesperR, SchneringHGV, CurdaJ. Li12Si7, eine Verbindung mit trigonal-planaren Si4-Clustern und isometrischen Si5-Ringen[J]. European Journal of Inorganic Chemistry, 1986, 119(12): 3576−3590. (in German)

[34] Dębski A, Gąsior W, Góral A. Enthalpy of formation of intermetallic compounds from the Li-Si system[J]. Intermetallics, 2012, 26: 157−161.

[35] Braga M H, Malheiros L F, Ansara I. Thermodynamic assessment of the Li-Si system[J]. Journal of Phase Equilibria, 1995, 16(4): 324−330.

[36] AXEL H, SCHÄFER H, WEISS A. The crystalline structure of lithium silicide Li2Si[J]. Applied Chemistry, 1965, 77(8): 379−380. (in German)

[37] LAI S C. Solid lithium-silicon electrode[J]. Journal of the Electrochemical Society, 1976, 123(8): 1196−1197.

[38] FRANK U, MÜLLER W, SCHÄFER H. To get the knowledge of the phase Li13Si4[J]. A Journal of Chemical Sciences, 1975, 30(1/2): 10−13. (in German)

[39] SCHÄFER H, AXEL H, WEISS A. Notes: The crystalline structure of the phase Li7Si2[J]. A Journal of Chemical Sciences, 1965, 20(10): 1010. (in German)

[40] KUBOTA Y, ESCAÑO M C S, NAKANISHI H, KASAI H. Crystal and electronic structure of Li15Si4[J]. Journal of Applied Physics, 2007, 102(5): 053704−053706.

[41] NESPER R, SCHNERING H G V. Li21Si5, a Zintl phase as well as a Hume-Rothery phase[J]. Journal of Solid State Chemistry, 1987, 70(1): 48−57.

[42] AXEL H, SCHÄFER H, WEISS A. To get the knowledge of the phase Li22Si5[J]. A Journal of Chemical Sciences, 1966, 21(2): 115−117.(in German)

[43] Dębski A, Zakulski W, MAJOR L, Góral A, GASIOR W. Enthalpy of formation of the Li22Si5intermetallic compound[J]. Thermochimica Acta, 2013, 551: 53−56.

[44] Morozkin A V. Phase equilibria in the Dy-V-Si system at 1200 K[J]. Journal of Alloys and Compounds, 2002, 346(1): L4−L6.

[45] Colinet C, Tedenac J C. First principles calculations in V-Si system. Defects in A15-V3Si phase[J]. Computational Materials Science, 2014, 85: 94−101.

[46] Meschel S V, Kleppa O J. Standard enthalpies of formation of some 3d transition metal silicides by high temperature direct synthesis calorimetry[J]. Journal of Alloys and Compounds, 1998, 267(1): 128−135.

[47] Rawn C J, Schneibel J H, Fu C L. Thermal expansion anisotropy and site occupation of the pseudo-binary molybdenum vanadium silicide Mo5Si3-V5Si3[J]. Acta Materialia, 2005, 53(8): 2431−2437.

[48] Gorelkin O S, Mikhailikov S V. Thermochemistry of the V-Si system[J]. Russian Journal of Physical Chemistry A, 1971, 45: 2682−2683. (in Russian)

[49] SPINAT P, FRUCHART R, HERPIN P. Structures of binary phases V6Si5and Ti6Ge5[J]. Bulletin of French Mineralogy and Crystallography Society, 1970, 93(1): 23−36. (in French)

[50] Tanaka K, Nawata K, Inui H, YAMAGUCHI M, KOIWA M. Refinement of crystallographic parameters in transition metal disilicides with the C11b, C40 and C54 structures[J]. Intermetallics, 2001, 9(7): 603−607.

[51] Kirklin S, Meredig B, Wolverton C. High-throughput computational screening of new Li-ion battery anode materials[J]. Advanced Energy Materials, 2013, 3(2): 252−262.

[52] Tao Xiao-ma, Chen Hong-mei, Tong Xiao-feng, OUYANG Yi-fang, JUND P, TEDENAC J C. Structural, electronic and elastic properties of V5Si3phases from first-principles calculations[J]. Computational Materials Science, 2012, 53(1): 169−174.

[53] WU Zhi-jian, Zhao Er-jun, Xiang Hong-ping, HAO Xian-feng, LIU Xiao-juan, MENG Jian. Crystal structures and elastic properties of superhard IrN2and IrN3from first principles[J]. Physical Review B, 2007, 76(5): 054115.

[54] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1954, 45(367): 823−843.

First-principles of Li-insertion properties of VSi2

LONG Ke-cheng1, 2, LI Zhi1, 2, DING Jing3, LONG Zhao-hui1, 2, LI Xiao-bo1, 2, YIN Fu-cheng1, 2

(1. Key Laboratory of Materials Design and Preparation Technology of Hunan Province, Xiangtan University, Xiangtan 411105, China; 2. School of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, China; 3. School of Metallurgy and Environment, Central South University, Changsha 410083, China)

First-principles calculation based on the density functional theory was employed to calculate the Li-insertion formation energy, specific capacity and volume expansion rate of every possible reactions of Li intercalation into VSi2. VSi2can react with Li, and the most possible reaction pathway of Li intercalation into VSi2is found. Firstly, Li reacts with VSi2to form Li13Si4and V5Si3, then Li reacts with Li13Si4to produce Li21Si5, while V5Si3cannot react with Li. So, the final reactants are V5Si3and Li21Si5. The 0K phase diagram of Li-Si-V ternary system can be determined by analyzing the reaction pathway of Li intercalation into VSi2. The electronic structure and elastic properties of VSi2and V5Si3were calculated further. The results show that both VSi2and V5Si3are characterized with a metallic conductor, but the conductivity and ductility of V5Si3, production after Li-insertion, are better than those of VSi2substrate. The results of calculation predict that V5Si3can act as a buffer phase to release the mechanical stress due to volume change during cycling of the electrode and a conductive agent to provide better conductivity, while improve the cycle performance of lithium intercalation/extraction.

first-principles; VSi2; Li-insertion properties; phase diagram; electronic structure; elastic properties

(编辑 李艳红)

Project (51471140) supported by the National Natural Science Foundation of China

2016-10-25;

2017-06-09

LI Zhi; Tel: +86-18907324649; E-mail: lizhiclsj@163.com

国家自然科学基金资助项目(51471140)

2016-10-25；

2017-06-09

李 智，教授，博士；电话：18907324649；E-mail：lizhiclsj@163.com

10.19476/j.ysxb.1004.0609.2018.01.18

1004-0609(2018)-01-0150-10

TG146.4；O646

A