采用相场法研究γ′相的析出动力学

孙向尚扬，赵 彦, ，鲁晓刚, ，孙晓峰，周 廉



采用相场法研究′相的析出动力学

孙向尚扬1, 2，赵 彦1, 2, 4，鲁晓刚1, 2, 4，孙晓峰3，周 廉4

(1. 上海大学 省部共建高品质特殊钢冶金与制备国家重点实验室，上海 200444；2. 上海大学 材料科学与工程学院，上海 200444；3. 中国科学院 金属研究所，沈阳 110016；4. 上海大学 材料基因组工程研究院，上海 200444)

通过相场法研究了1073K时效过程中Ni-Al高温合金′相的析出动力学。结果表明：在形核长大阶段，随Al成分增加，′相的生长动力学指数值总体呈下降趋势，当≈0.5(为′相半径与平均半径的比值)时，′相数目达到最大，小于该尺寸的′相几乎不存在。在′相的粗化阶段，′相的生长动力学指数值介于2~3之间，′相的生长机制为溶质扩散与界面迁移共同作用的混合机制。粗化阶段′相的尺寸分布符合Gamma分布，且粗化后期满足标度律。在′相的粗化后期，随时间的延长，′相的尺寸均匀性越好，且随Al成分增加，′相的粗化机制有从溶质扩散机制向界面迁移机制的过渡。

镍基高温合金；相场法；析出动力学；生长机制；动力学指数

镍基高温合金以其较高的高温强度、良好的塑韧性以及优良的耐疲劳、抗氧化、抗热腐蚀等性能[1−3]，被用于航空发动机的四大热端部件(导向器、涡轮叶片、涡轮盘和燃烧室)。当前，镍基单晶合金已经发展到第五代，使用温度高达1100 ℃以上，其优异的高温力学性能与在基体-Ni相共格析出具有L12结构的′-Ni3Al相有着密切联系，其中′相体积分数甚至高达65%以获得尽可能好的强化效果[4]。因此，通过理论模拟[5−9]和科学实验研究[10−15]热处理过程中的′相的析出行为仍是研究热点之一。

至今为止，′相的析出动力学的研究包括了实验和计算模拟方法，所采用的实验手段主要包括了TEM、APFIM、HREM、SWNS等。HIRATA等[11]通过TEM方法研究了′相的析出行为并计算了′相的形核率，WENDT等[12]利用原子探针场离子显微镜技术(APFIM)发现，即使在过饱和度很小的合金中，′相的形核也能在很短的时间内完成。XIAO等[13]利用高分辨电子显微镜技术(HREM)研究′相早期析出沉淀 行为。

而另一方面，通过计算机模拟′相的析出也成为研究′相的析出行为的重要手段，模拟方法主要包括解析法、相场法、Monte Carlo法、有限元法等，其中，相场法在′相的析出动力学的研究中具有一定模型上的优势，其通过在自由能泛函中引入体自由能、界面能、弹性能等的影响，可有效地模拟复杂条件下的′相的析出行为。SIMMONS等[16]采用相场方法研究了等温和非等温条件下的′相的析出行为，WEN等[17]通过相场法模拟了连续过程过程中的二次′相的析出行为，ZHU等[18]建立了模拟′相生长的KKS模 型等。

在实验和模拟基础上，统计分析′相的析出行为所得到的规律性结果将为认知和改进热处理工艺提供有效帮助。当前，显微组织生长行为统计规律的讨论可分类两类：一类以显微组织形貌特征数据进行分析，如体积分数、颗粒尺寸分布、平均半径、′相的长宽比等[19−20]，选择恰当的形貌特征分析数据能够有效地给出显微组织的生长机制[ 21−25]、分布特征等信息；另一类以结构函数和动力学标度给出了显微组织生长过程中的谱规律对显微组织生长动力学进行研究，这在研究非晶、有序化等过程中得到应用[26]。借助显微组织的统计分析方法，并将其引入′相的生长动力学的讨论，无疑将有助于解析′相的析出机制。

基于此，本文作者利用相场法研究了1073 K时效过程中Ni-Al高温合金′相的析出动力学，包括′相的形核动力学与粗化动力学行为。通过研究形核长大阶段′相的生长动力学指数与′相的半径与平均半径的比值确定′相的生长机制；研究粗化阶段的′相的尺寸分布及标度律分析′相的粗化机制，最终解析′相的析出机制。

1 计算模型

二元合金的有序态可通过溶质原子在晶格位置的占位几率()进行描述，()的表达式可写为[27]

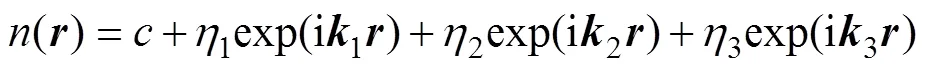
其中，

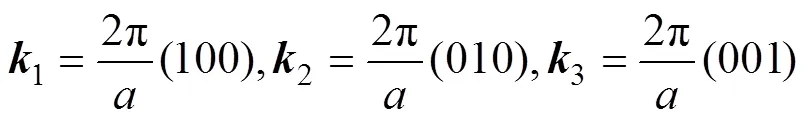
式中：为波矢量；为晶格常数；为溶质原子的成分；1、2、3为长程序参数，对应溶质原子成分波的波幅，当1=2=3=0，所有亚晶格位置的占位几率相等均为，由式(1)表示的晶体结构为FCC固溶体；当1=2=3=，面心立方晶胞顶角位置的占位几率1=+3，面心位置的占位几率2=c−，则式(1)表示12晶体结构；当1=且2=3=0，或2=且1=3=0，或3=且1=2=0时，式(1)描述3种取向的L10晶体结构。

采用(1,2,3)=(0, 0, 0)表征相；(1,2,3)=(1, 1, 1)，(1,2,3)=(−1, 1, 1)，(1,2,3)=(1, −1, 1)和(1,2,3)=(1, 1, −1)表征′相。

为研究′相的析出动力学，计算模型中考虑了溶质原子扩散和有序化，方程采用求解保守场参数的Cahn-Hillard方程(3)和求解非保守场参数的Ginzburg-Landau方程(4)：

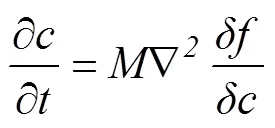
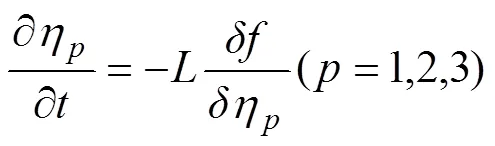
式中：、为动力学常数；为时间；为自由能泛函。

其表达式为

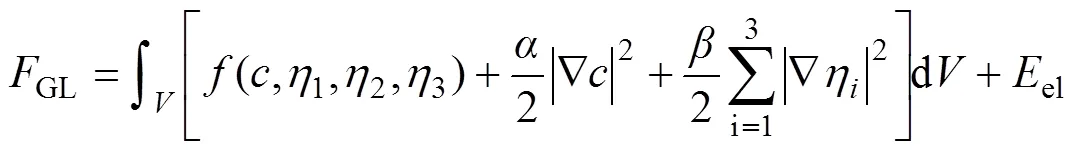
式中：(,1,2,3)为单位体积均匀有序相的非平衡自由能密度函数；和是梯度能系数；el为弹性能。根据弹性力学理论，仅需要3个弹性常数11、12、44即可表征晶体的对称性。因此，对el进行了简化，选用WANG等[28]推导的简化形式：

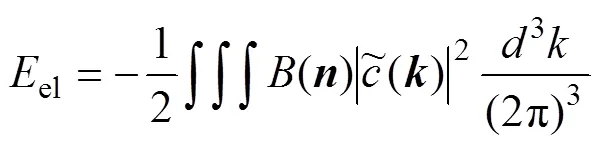
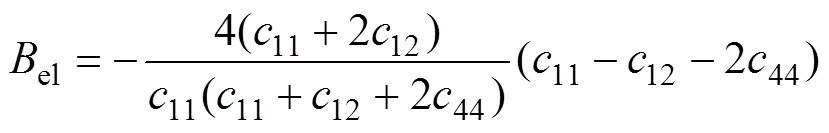
从函数的表达式中看出：el的取值决定弹性应变能的大小，el的符号决定弹性各向异性对应的情况。因此，仅需要改变el的取值即可表示系统所受的弹性应变能大小。

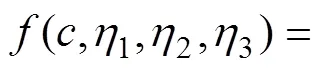
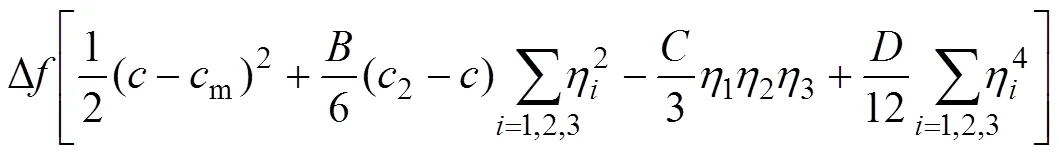
式中：Δ是模型的自由能密度；2是任意成分，取值在相平衡成分m与′相的平衡成分p之间，这里定义2=0.15；、、为正数，为保证相和′相的自由能阱深相等，参数的取值分别为

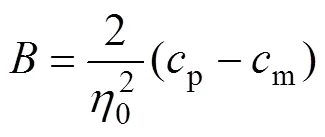
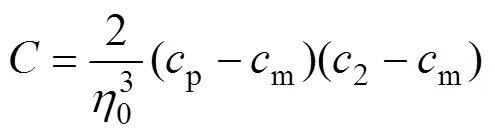
模拟中所采用参数的取值：Δ5×107erg/cm3、0=1、m=0.135、p=0.234、2=0.15、==1、=0.28、=0.1。由此所得到的、、值与Ni-Al合金1073K条件下的Gibbs自由能数据匹配较好，可用于计算。

2 结果与讨论

2.1 1073K时效时γ′相的析出形貌

2.1.1 Ni-Al合金1073K时效时′相的模拟结果

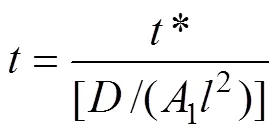
图1 Ni-Al合金1073K时效时γ′相的形貌演化

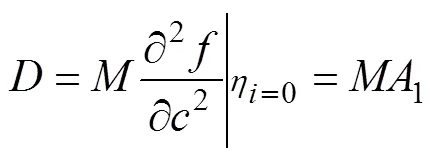
式中：*为时间步；为矩阵长度；1为多项式系数，1=40。

根据文献[11]的取值，选择=6.51×10−15cm2/s。设置512×512矩阵表示′相的形貌演化的区域，相邻两矩阵单元之间所代表的实际空间尺寸为=19Å。系统的初始状态为Al成分Al=0.18的均匀过饱和固溶体，代表基体相。成分起伏作用下，′相开始形核(见图1(a))，析出的′相尺寸较小，弥散分布且呈球状，从灰度的对比不难发现，此时′相的成分与基体相近；到270步时，系统内形成大量的′相的并逐步长大(如图1(b))，此时，′相的形貌仍旧没有明显的取向性；在弹性应变能作用下，′相的形貌演变为方块状，并择优沿á100ñ方向生长，与图1(b)中的′相的形貌相比，此时′相的明显发生粗化(见图1(c))，1200步时，尺寸较小且数目较多的′相逐渐演变为尺寸较大、数目较少的′相；在随后的时效过程中，′相尺寸进一步长大，到30000步时，′相的尺寸稳定，最终形貌如图1(d)所示。

2.1.2 不同合金成分′相的析出行为

图2所示为′相的平均半径和数目随时间的演化。从图2中可以看到，′相的平均半径的演化大致经历了4个阶段：第一阶段为′相的形核孕育期，该阶段没有′相的析出，′相的平均半径和数目均为0；第二阶段为′相的形核长大阶段，在该阶段，′相的析出相的数目和平均尺寸均快速升高，标志大量′相的小核心形成，并长大；达到峰值后，进入第三阶段，该阶段发生了′相粗化，此时，′相的体积分数没有明显变化，但′相间相互结合，使得′相数目减小，平均尺寸逐步升高；第四阶段，′相数目和平均尺寸基本达到平衡。

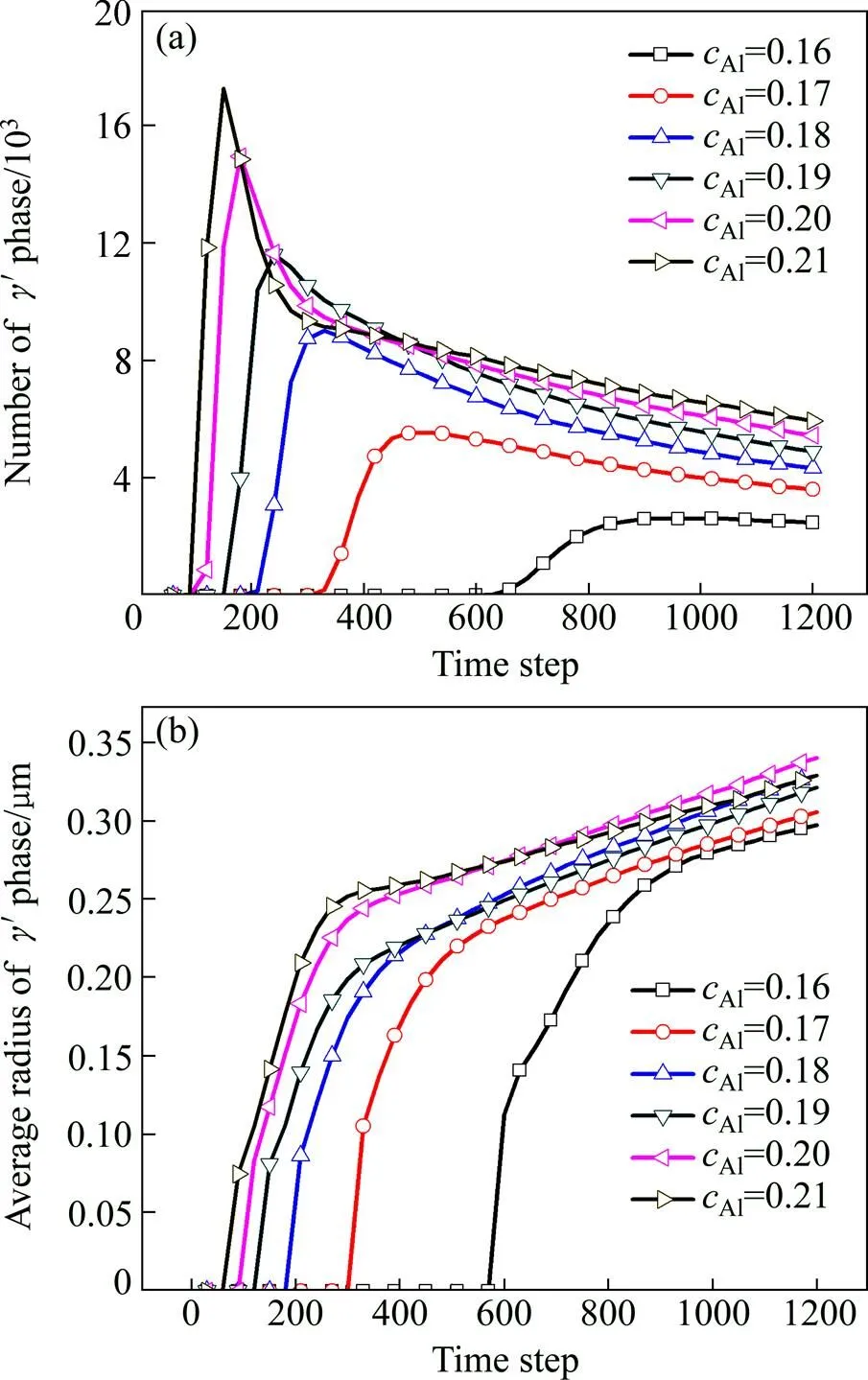
图2 不同成分下γ′相数目与平均半径随时间的演化

根据′相数目演化峰值出现的时刻，可把′相的生长行为划分为形核长大和粗化两个阶段。形核长大阶段，′相的核不断析出并逐步长大使得′相的颗粒数目和尺寸均增加；而粗化阶段，′相的相互合并，导致尺寸虽然继续增大，但由于′相合并，使得′相数目大幅下降。此外，依′相的平均半径的演化显示，形核长大阶段′相的生长速度较快，而粗化阶段的生长速度相对较慢(见图2(b))。

实际合金的′相的生长行为应是′相的形核、长大及粗化同时进行、协同推进、相互重叠的过程，难以进行阶段性划分，但不同时期′相的生长行为，有主要的生长行为控制，且大多数的′相生长行为决定该阶段进入怎样的生长阶段。

2.2 形核长大阶段γ′相的生长动力学机制

2.2.1 形核长大阶段′相的生长动力学

根据LSW理论[21]，相颗粒的生长行为满足Wagner-Lifshitz方程：

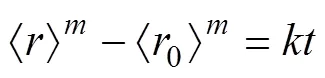
式中：和0分别为时刻和初始时刻的相颗粒平均尺寸；为动力学指数[30]；为相颗粒生长速率相关的常数。一般地，式(11)主要用于描述粗化阶段相颗粒生长后期的动力学行为。最近研究发现，在相颗粒生长前期，也具有相似的动力学行为，如满足动力学标度律等[31]。

根据式(11)，析出相平均尺寸的幂次方与时间满足线性关系。对式(11)进行线性变换，得到以下公式：

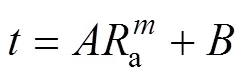
式中：A、B为常数；Ra为析出相平均尺寸；m为动力学指数。由式(12)对形核长大阶段γ′相的平均尺寸演化进行了拟合。图3所示为Ni-Al合金形核长大阶段γ′相的平均半径演化的模拟结果与拟合结果的对比。图3中显示，拟合结果与模拟结果匹配较好，说明通过该方法研究γ′相的生长行为具有一定合理性。

表1对拟合参数值进行了整理。从表1中可看到，随着Al成分增加，值总体上减小，说明′相的长大速度总体较快。但也发现，当Al＞0.19时，该规律失效。由此可知，随Al成分增加，形核长大阶段′相的生长速度并不呈线性关系。究其原因在于：当Al成分较低时，随Al成分增加，基体的过饱和度越大，促使′相的长大速度也越快，而当Al＞0.19时，随Al成分增加，由于形核初期的形核率增加导致，′相的生长过程中基体的过饱和度反而减少，从而增加了′相的生长速度的不确定性。

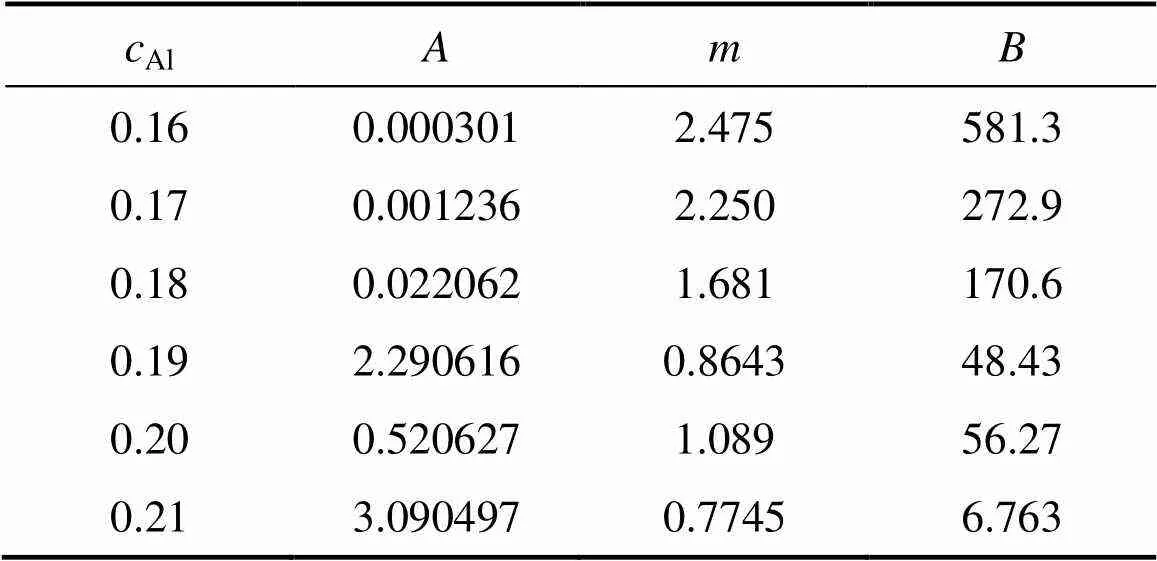
表1 形核长大阶段t=ARam+B公式对γ′相的平均半径演化非线性拟合得到的参数值

2.2.2 形核长大阶段′相的尺寸分布

为定性描述Ni-Al合金早期的形核长大行为，选择UDIMET720Li合金的实验结果与本文的模拟结果进行了对比。图4所示为不同冷却速率时UDIMET720Li合金′相的尺寸与析出数量的关系[32]。在该过冷条件下，′相的发生了多次析出，生成了多次′相，特别注意到，在0.0167K/s的冷速下，三次′相与四次′相的尺寸分布并没有完全分开，而已经分开的′相的尺寸分布呈正态分布特征。这意味着四次′相仍处于形核长大阶段，此时四次′相的尺寸分布的形貌与模拟结果相似(见图5(a))，包络线具有对数函数的曲线特征，间接证明了模拟结果的合理性。

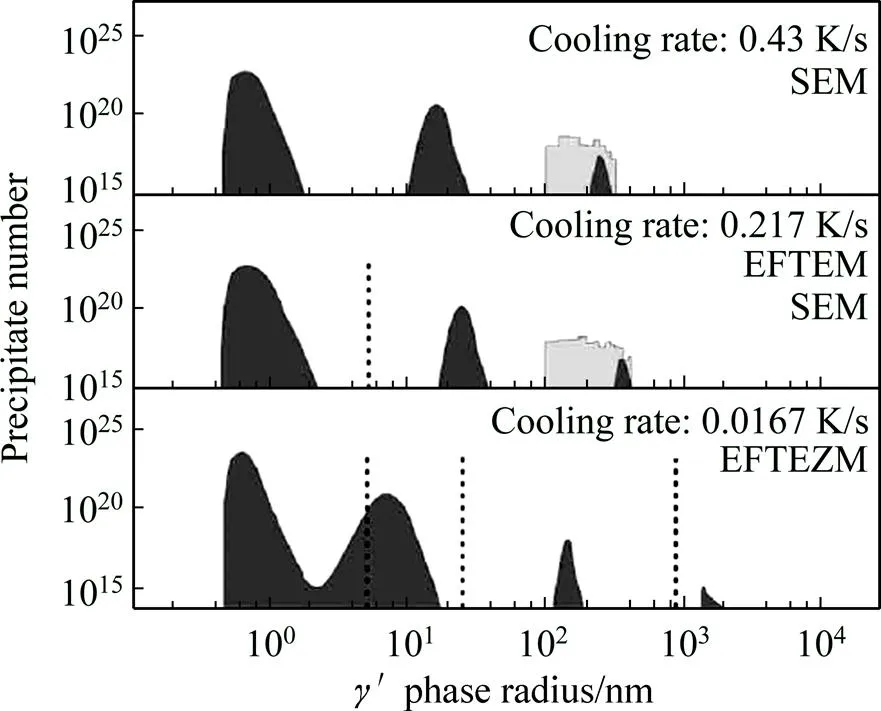
图4 不同冷却速率时UDIMET720Li合金γ′相的尺寸与析出数量的关系[32]

图5所示为形核长大阶段′相的尺寸分布。其中横坐标为′相半径与平均半径áñ的比值，说明′析出相的相对大小；纵坐标为′相尺寸的分布密度。从图5中看到，此时′相的尺寸分布不再服从正态分布，而具有对数函数分布的特征。

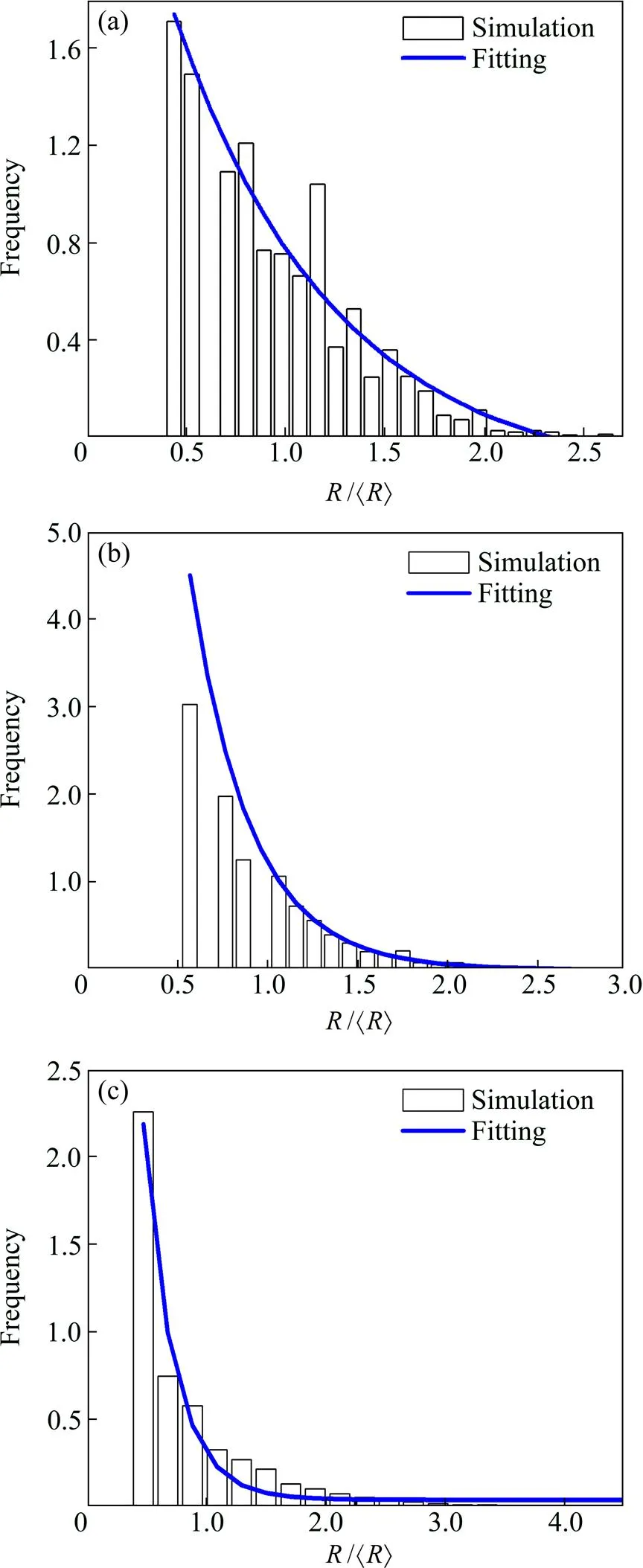
图5 通过函数f(ρ)=A×C−Dρ+B拟合的不同成分Ni-Al合金形核长大阶段γ′相尺寸的分布对比

根据尺寸分布的情况，本文作者建立了拟合′相的尺寸分布的拟合函数，形式为()=×−Dρ+。其中、、、为拟合参数；=/áñ。其拟合结果在图5中进行了显示，从拟合结果看，拟合函数与模拟结果匹配较好，此外，从拟合结果看到，随Al成分增加，′相的尺寸分布曲线的弯曲度增大，这说明在形核长大阶段，大尺寸′相的比例随Al成分增加而逐渐减小，小尺寸′相的比例随Al成分增加而进一步增大。Al成分增大更有利于促进′相的核生成。

2.3 粗化阶段γ′相的生长动力学机制

2.3.1 粗化阶段′相的生长动力学

图6同样借助相颗粒生长动力学公式=a+对粗化阶段′相的生长行为进行了拟合。由图6可看出，模拟结果与拟合结果也具有较好的一致性。

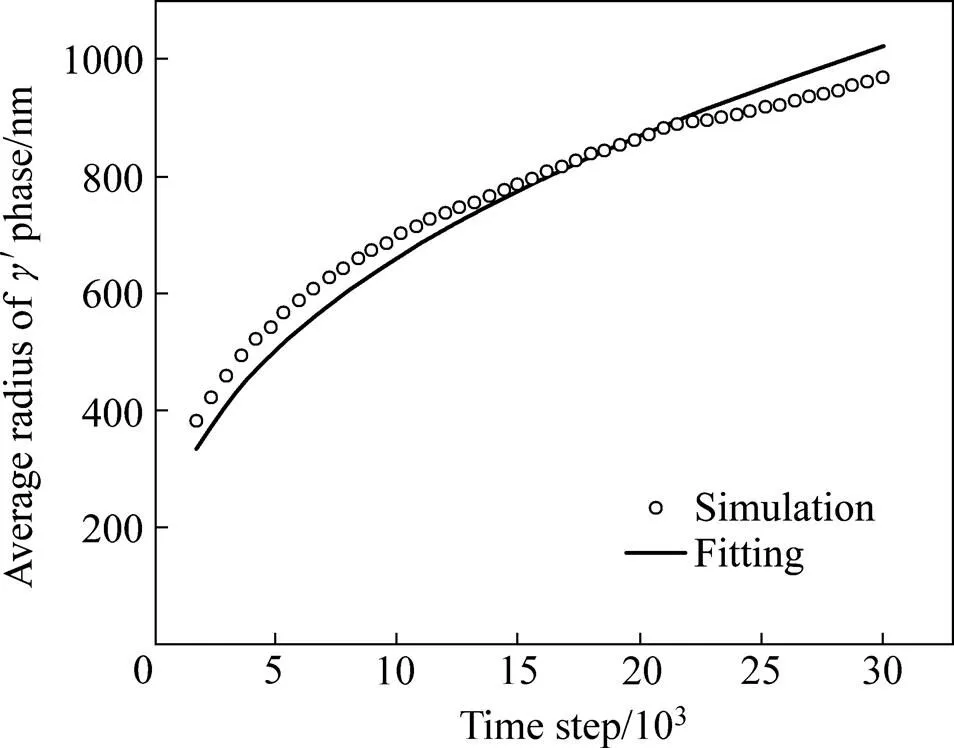
图6 Ni-Al合金粗化阶段γ′相半径Ra随时间演化的模拟结果与t=ARam+B非线性拟合的结果对比

通过对Al为0.16~ 0.21这6种成分下′相的生长行为的拟合，得到如表2的拟合参数值。从表2中看到，′相生长动力学指数的取值在2~3之间，较形核长大阶段′相的生长动力学指数值要高，说明该阶段′相的生长速度明显减慢。根据相颗粒生长一般结果，溶质扩散型相颗粒生长的动力学指数的取值为3[33]，而界面迁移型相颗粒生长的动力学指数的取值为2[34]，从所得到的模拟结果发现，粗化阶段的′相的生长动力学指数值刚好介于两种粗化机制之间，即说明′相的粗化行为同时受到溶质扩散和界面迁移的作用。由于弹性应变能的作用，使得′相的生长具有各向异性特征，在′相粗化阶段，受生长方向限制，溶质原子的扩散及′相的界面的迁移主要沿á100ñ方向进行，导致两种机制发生交叉，因此其生长动力学指数在2~3之间。VAITHYANATHAN等[35]曾对=3时′相的生长行为进行了线性表示，线性拟合结果与′相的生长行为有较好的一致性，但本研究显示的取值并非等于3，而是介于2~3之间才更精确，说明粗化阶段′相的生长机制是溶质扩散和界面迁移的混合机制。

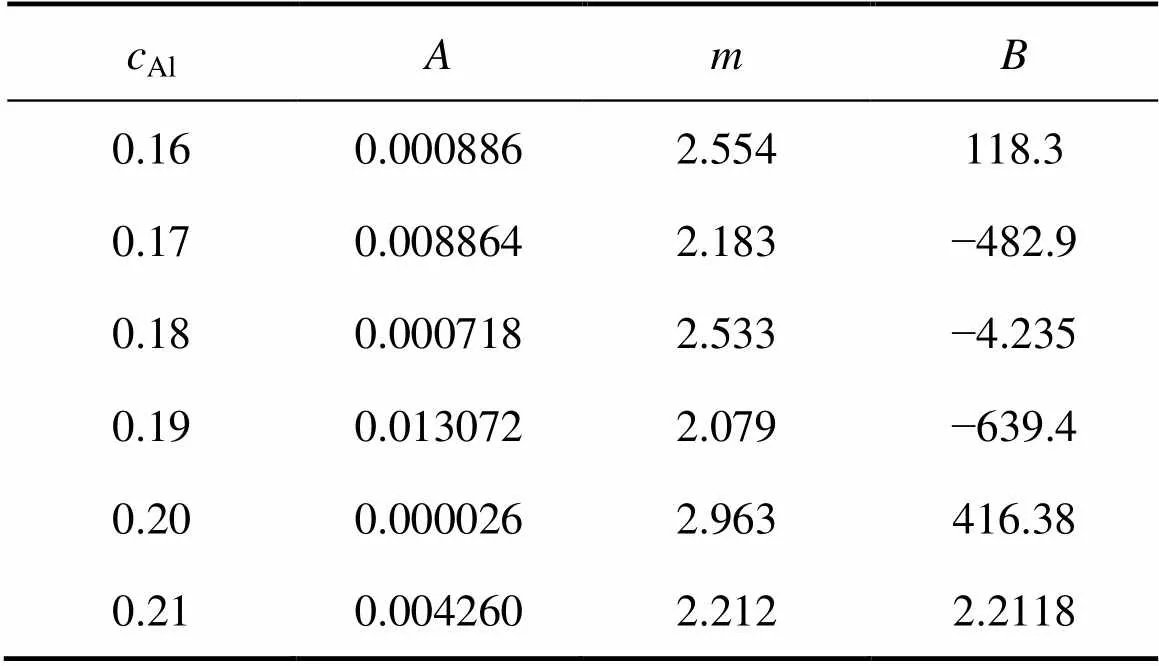
表2 粗化阶段t=ARam+B公式对γ′相的平均半径演化非线性拟合的参数值

2.3.2 粗化阶段′相的尺寸分布

通过7种分布函数[36]对粗化阶段的′相尺寸分布进行拟合，从而进一步研究′相的粗化机制，并探究了Al成分对′相的尺寸分布的影响。

7种分布函数在表3中进行了显示，公式中=/áñ，、、为拟合参数。

2.3.2.1 分布函数与′相的尺寸分布的对比

图7所示为7种分布函数拟合粗化阶段′相尺寸分布的结果对比。图7(a)中显示了Hillert、Wagner(1) 及Wagner(2)分布函数拟合结果与′相的尺寸分布的对比。从结果看，3种分布函数峰所对应的值偏向=1的右侧，而′相的尺寸分布的峰偏向=1的左侧，两者的偏差很大，这从侧面反映′相的粗化行为并不满足理想相颗粒粗化动力学行为，难以用扩散控制或界面迁移控制颗粒生长机制表征′相的粗化行为。

图7(b)显示了Lorgnormal、Weibull、Gamma、Rayleigh函数分布的拟合结果。从图中看到，Lorgnormal和Weibull函数拟合的结果仍存在较大偏差，但可准确定位曲线峰的值位置。Gamma函数和Rayleigh函数的拟合结果与′相的尺寸分布有较好的对应关系，其原因在于两种函数的拟合参数相对较多，因而函数能有更多的变化。

表3 拟合粗化阶段′相的尺寸分布函数

Table 3 Distribution functions of′ phase size distribution at fitting coarsening stage

2.3.2.2 分布函数随时间和Al成分的变化

经多种Al成分下′相的尺寸分布拟合结果比较发现，Gamma函数有更好的拟合结果，故使用Gamma函数拟合′相的尺寸分布曲线。

图8所示为Ni-Al合金1073K时效时′相的粗化阶段几个不同时刻的′相的尺寸分布与不同Al成分下′相的尺寸分布。从图8(a)中看到，粗化阶段′相数目的峰值出现在0.7左右，反映出′相尺寸的差异性较大，这使得较大的′相虽然数目较少，但尺寸相对较大。

从图8中也观察到，随时间演化′相的尺寸分布的峰值所对应的值有升高的趋势，说明在粗化过程中′相尺寸逐渐均匀化。而12000步后，′相的尺寸分布几乎重合在一起。粗化阶段′相的半径虽然增长，但其尺寸分布则没有变化，这意味着′相的粗化后期符合标度生长法则，′相的后期生长仅仅是尺寸大小发生了变化，而′相的相对尺寸并未受到影响，其生长行为具有自相似性，即满足标度律。

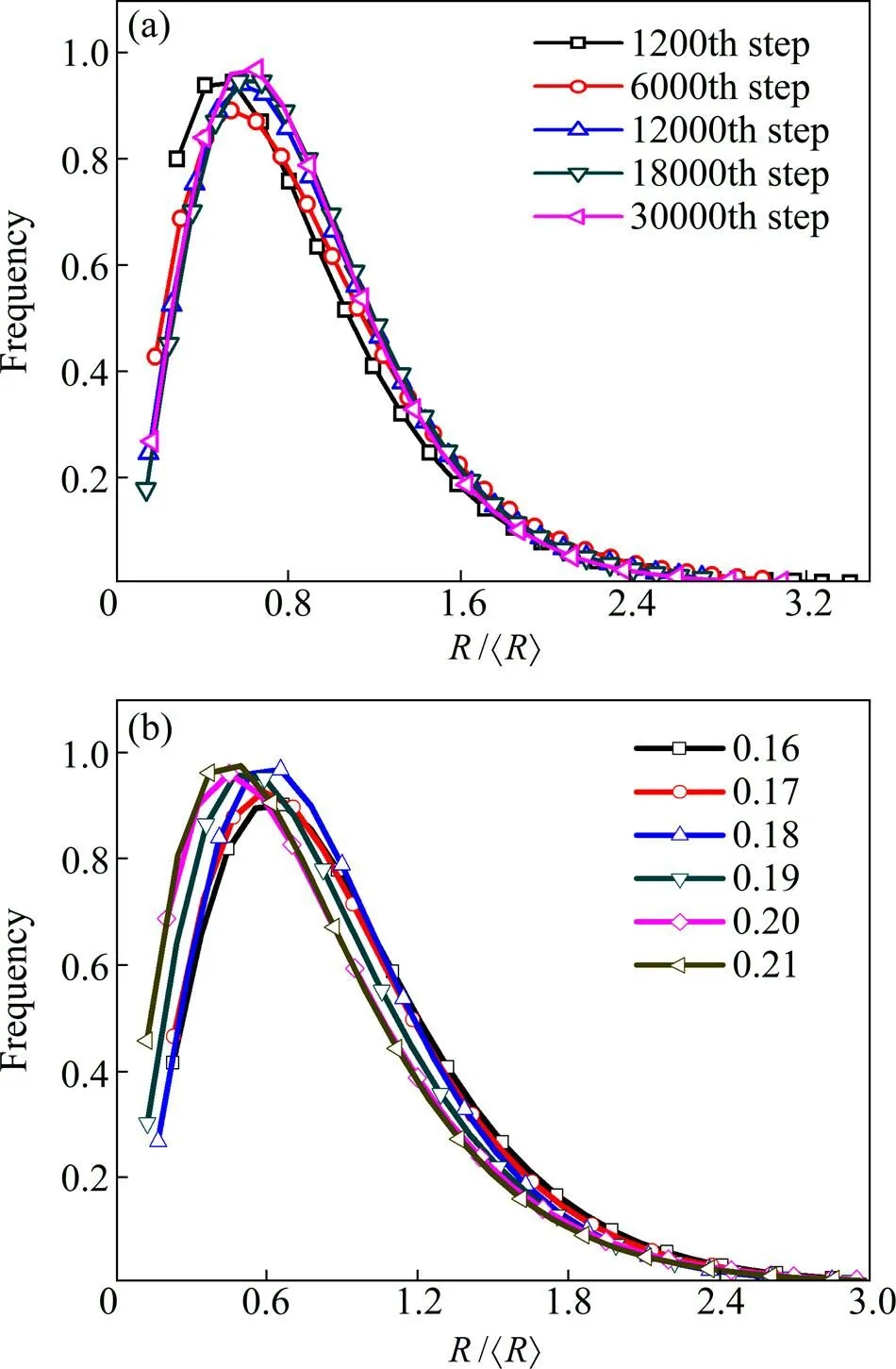
图8 Ni-Al合金1073K时效过程γ′相的尺寸分布随时间的演化与不同Al成分下γ′相的尺寸分布

图7(b)显示了不同成分′相的尺寸分布。从图8(b) 中看到：随Al成分增加，′相的尺寸分布曲线的峰值逐步升高，且曲线峰逐步向较小值方向过渡。曲线峰值升高的结果说明，在峰所对应的值区间有较多′相存在，而对于曲线峰逐步向小值方向过渡，意味着′相的粗化阶段，较小尺寸的′相数目相对较多。该现象的原因在于：在较小Al成分时，′相的粗化行为主要通过Oswald粗化方式进行，体扩散起了较大作用，而界面迁移导致′相的粗化的因素相对较弱，这使得′相的均匀性相对较高。随着Al成分增加，形核长大过程中有较多的′相析出，′相间的距离减小，体扩散导致′相的粗化的因素逐渐减弱，而界面迁移导致′相的粗化的因素逐渐增强，从而使得界面迁移导致从形核长大阶段过渡到粗化阶段，′相的数目快速减少的同时，也使得′相的尺寸的差异性增大。此外，从模拟结果同时看到，不论Ni-Al合金中Al成分大小如何，大于3倍平均尺寸的′相几乎不存在，这与形核阶段的′相的尺寸分布相似，存在一个阈值把′相的尺寸划分为两部分，超越阈值范围内的′相的几乎不存在。

3 结论

1) 在形核长大阶段，随Al成分增加，′相的生长动力学指数值总体呈下降趋势，从′相的生长行为难以判定该阶段′相的生长机制，根据该阶段′相的尺寸分布可知，当=0.5左右时，′相的数目达到最大，小于该尺寸的′相几乎不存在。

2) 在′相的粗化阶段，′相的生长动力学指数值介于2~3之间，′相的生长机制为溶质扩散与界面迁移共同作用的混合机制。粗化阶段的′相的尺寸分布符合Gamma分布，且粗化后期满足标度律。

3) 在′相的粗化后期，随时间演化′相的尺寸均匀性变好，当Al成分增加，′相的粗化机制有从溶质扩散机制向界面迁移机制的过渡。

[1] 于兴福, 杜洪强, 田素贵, 宁 英, 王铁军, 崔树森. 无铼二代镍基单晶高温合金中温高应力蠕变机制[J]. 中国有色金属学报, 2012, 22(7): 1921−1928. YU Fu-xing, DU Hong-qiang, TIAN Su-gui, NING Ying, WANG Tie-jun, CUI Shu-sen. Creep deformation mechanism in Re free second generation nickel-base single crystal superalloy during medium temperature and high stress[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 1921−1928.

[2] 苏 勇, 田素贵, 于莉丽, 于慧臣, 张 姝, 钱本江. [111]取向镍基单晶合金的组织结构与蠕变行为[J]. 中国有色金属学报, 2012, 22(6): 1624−1631. SU Yong, TIAN Su-gui, YU Li-li, YU Hui-chen, ZHANG Shu, QIAN Ben-jiang. Microstructure and creep behavior of [111] orientation single crystal nickel-based superalloy[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(6): 1624−1631.

[3] SHI Zhen-xue, LI Jia-rong, LIU Shi-zhong, WANG Xiao-guang, YUE Xiao-dai. Effect of Ru on stress rupture properties of nickel-based single crystal superalloy at high temperature[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2106−2111.

[4] YU Jin-jiang, SUN Xiao-feng, ZHAO Nai-ren, JIN Tao, GUAN Heng-rong, HU Zhuang-qi. Effect of heat treatment on microstructure and stress rupture life of DD32 single crystal Ni-base superalloy[J]. Materials Science and Engineering A, 2007, 460: 420−427.

[5] 田素贵, 陈昌荣. 单晶 Ni 基合金高温蠕变期间′相定向粗化驱动力的有限元分析[J]. 金属学报, 2000, 36(5): 465−471. TIAN Su-gui, CHEN Chang-rong. Finite element analysis of driving force of′ phase directional coarsening for a single crystal Nickel-base superalloy during high temperature creep[J]. Acta Metall Sin, 2000, 36(5): 465−471.

[6] 周广钊, 王永欣, 陈铮. 三维相场法模拟弹性能作用下 Ni 基合金′相颗粒的粗化动力学[J].稀有金属材料与工程, 2014, 43(4): 916. ZHOU Guang-zhao, WANG Yong-xin, CHEN Zheng. Three-dimensional phase-field method simulation of coarsening kinetics of′ particles under elastic energy in Ni base alloys[J].Rare Metal Material And Engineering, 2014, 43(4): 916.

[7] 彭志方, 任遥遥, 张 伟, 燕 平, 赵京晨, 王延庆. Ni 基单晶高温合金原树枝状晶结构典型区域和′相成分的测算[J]. 金属学报, 2001, 37(4): 345−352. PENG Zhi-fang, REN Yao-yao, ZHANG Wei, YAN Ping, ZHAO Jing-chen, WANG Yan-qing. Estimation ofand′ phase compositions in typical regions of original dendrite structure of Nickel-base single crystal superalloy CMSX-2[J]. Acta Metall Sin, 2001, 37(4): 345−352.

[8] 石宇野, 焦少阳, 董建新, 张麦仓. 镍基高温合金′相析出的经典动态模型及应用[J]. 金属学报, 2012, 48(6): 661−670.SHI Yu-ye, JIAO Shao-yang, DONG Jian-xin, ZHANG Mai-cang.Classical precipitation dynamic model of′ phase of nickel-based super alloys and applications[J]. Acta Metall Sin, 2012, 48(6): 661−670.

[9] 李 奇, 秦鹤勇, 郭翠萍, 孟 晔, 郑 磊. 镍基高温合金GH4706析出相的热力学计算与分析[J]. 钢铁研究学报, 2017, 29(3): 208−215. LI Qi, QIN He-yong, GUO Cui-ping, MENG Ye, ZHENG Lei.Thermodynamic calculation and theoretical analysis of equilibrium precipitation phases in Ni-based superalloy GH4706[J]. Journal of Iron and Steel Research, 2017, 29(3): 208−215.

[10] 郭 岩, 侯淑芳, 王博涵, 林 琳. 固溶强化型镍基合金的时效析出行为[J]. 中国电力, 2013, 46(9): 34−38. GUO Yan, HOU Shu-fang, WANG Bo-han, LIN lin. Aging precipitation behavior of solid-solution strengthened nickel-base alloys[J]. Electric Power, 2013, 46(9): 34−38.

[11] HIRATA T, KIRKWOOD D H. The prediction and measurement of precipitate number densities in a nickel-6.05 wt.% aluminium alloy[J]. Acta Metallurgica, 1977, 25(12): 1425−1434.

[12] WENDT H, HAASEN P. Atom probe field ion microscopy of the decomposition of Cu-2.7at%[J]. Scripta Metallurgica, 1985, 19(9): 1053−1058.

[13] XIAO S Q, HAASEN P. HREM investigation of homogeneous decomposition in a Ni-12 at.% A1 Alloy[J]. Acta Metallurgica et Materialia, 1991, 39(4): 651−659.

[14] 郭 岩, 周荣灿, 侯淑芳, 张红军, 林 琳. 镍基合金的析出相及强化机制[J]. 金属热处理, 2011, 36(7): 46−50. GUO Yan, ZHOU Rong-can, HOU Shu-fang, ZHANG Hong-jun, LIN lin. Precipitates and strengthening mechanism in Ni-based alloys[J]. Heat Treatment of Metals, 2011, 36(7): 46−50.

[15] 杨 旭. 一种单晶高温合金中′相的析出行为[J]. 科学技术与工程, 2011, 11(15): 3523−3526. YANG Xu. The precipitation of′-phase in a single crystal superalloy[J]. Science Technology and Engineering, 2011, 11(15): 3523−3526.

[16] SIMMONS J P, WEN Y, SHEN C, WANG Y. Microstructural development involving nucleation and growth phenomena simulated with the phase field method[J]. Materials Science and Engineering A, 2004, 365(1): 136−143.

[17] WEN Y H, SIMMONS J P, SHEN C, WOODWARD C, WANG Y. Phase-field modeling of bimodal particle size distributions during continuous cooling[J]. Acta Materialia, 2003, 51(4): 1123−1132.

[18] ZHU J Z, WANG T, ARDELL A J, ZHOU S H, LIU Z K, CHEN L Q. Three-dimensional phase-field simulations of coarsening kinetics of′ particles in binary Ni-Al alloys[J]. Acta Materialia, 2004, 52(9): 2837−2845.

[19] DUHL M G D N, GIAMEI A. The development of single crystal superalloy turbine blades[J]. Superalloys, 1980, 41:205−214.

[20] 陈荣章. 单晶高温合金发展现状[J]. 材料工程, 1995(8): 3−12. CHEN Rong-zhang. Development status of single crystal superalloy[J]. Journal of Materials Engineering, 1995(8): 3−12.

[21] LIFSHITZ I M, SLYOZOV V V. The kinetics of precipitation from supersaturated solid solutions[J]. Journal of Physics and Chemistry of Solids, 1961, 19(1/2): 35−50.

[22] ZHANG S W, STEVENS R N, DAVIES C K L.′ particle coarsening in nickel-based alloys[J]. J Mater Eng, 1992(3): 17−19.

[23] XIA P C, YU J J, SUN X F, GUAN H R, HU Z Q. Influence of thermal exposure on′ precipitation and tensile properties of DZ951 alloy[J]. Materials Characterization, 2007, 58(7): 645−651.

[24] SAFARI J, NATEGH S, MCLEAN M. Evolution of microstructure of nickel base superalloy at high temperatures[J]. Materials Science and Technology, 2006, 22(8): 888−898.

[25] KIM D M, ARDELL A J. The volume-fraction dependence of Ni3Ti coarsening kinetics—New evidence of anomalous behavior[J]. Scripta materialia, 2000, 43(4): 381−384.

[26] 刘俊明, 吴状春, 刘治国. 非晶态Cu12.5Ni10Zr41Ti14Be22.5合金相分离的动力学标度[J]. 物理学报, 1997, 46(6): 1146−1152. LIU Jun-ming, WU Zhuang-chun, LIU Zhi-guo. Dynamic scaling of phase separation in amorphous Cu12.5Ni10Zr41Ti14Be22.5Alloy[J]. Acta Physica Sinica, 1997, 46(6): 1146−1152.

[27] KHACHATURYAN A G. Theory of structural transformations in solids Wiley[M]. New York: Wiley, 1983.

[28] WANG Y, BANERJEE D, SU C C, KHACHATURYAN A G. Field kinetic model and computer simulation of precipitation of L12 ordered intermetallics from FCC solid solution[J]. Acta materialia, 1998, 46(9): 2983−3001.

[29] LI D Y, CHEN L Q. Shape evolution and splitting of coherent particles under applied stresses[J]. Acta Materialia, 1998, 47(1): 247−257.

[30] LEBOWITZ J L, MARRO J, KALOS M H. Dynamical scaling of structure function in quenched binary alloys[J]. Acta Metallurgica, 1982, 30(1): 297−310.

[31] OHNOGI H, SHIWA Y. Nucleation, growth, and coarsening of crystalline domains in order-order transitions between lamellar and hexagonal phases[J]. Physical Review E, 2011, 84(1): 011611.

[32] RADIS R, SCHAFFER M, ALBU M, KOTHLEITNER G, PÖLT P, KOZESCHNIK E. Multimodal size distributions of γ′ precipitates during continuous cooling of UDIMET 720 Li[J]. Acta Materialia, 2009, 57(19): 5739−5747.

[33] ROGERS T M, ELDER K R, DESAI R C. Numerical study of the late stages of spinodal decomposition[J]. Physical Review B, 1988, 37(16): 9638.

[34] ALLEN S M, CAHN J W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening[J]. Acta Metallurgica, 1979, 27(6): 1085−1095.

[35] VAITHYANATHAN V, CHEN L Q. Coarsening of ordered intermetallic precipitates with coherency stress[J]. Acta Materialia, 2002, 50(16): 4061−4073.

[36] ROHRER G S. Influence of interface anisotropy on grain growth and coarsening[J]. Annu Rev Mater Res, 2005, 35: 99−126.

Precipitation kinetics of′ phase investigated by phase-field method

SUN Xiang-shang-yang1, 2, ZHAO Yan1, 2, 4, LU Xiao-gang1, 2, 4, SUN Xiao-feng3, ZHOU Lian4

(1. State Key Laboratory of Advanced Special Steel, Shanghai University, Shanghai 200444, China; 2. School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China; 3. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China; 4. Institute of Material Genome, Shanghai University, Shanghai 200444, China)

The kinetics of the′ phase precipitation for Ni-Al superalloys at 1073K was studied by the coherent phase-field method. The results shows that, at the nucleation and growth stages, as the Al composition increases, the kinetic exponentof′ phase growth shows an overall declining trend. It is difficult to determine the growth mechanism of the′ phase. According to the′ phase size distribution at the nucleation and growth stages, it is known that the number of′ phase particles reaches the maximum near=0.5 (is the ratio of′ phase radius to its average radius). The particles with size smaller than=0.5 are much less. During the coarsening stage, the range ofvalue is between 2 and 3. The growth mechanism of the′ phase is hybrid comprised of the solute diffusion mechanism and the boundary migration mechanism. The size distribution of′ phase at the coarsening stage approaches the Gamma distribution and satisfies the scaling rule at the late period of coarsening. Besides, as the Al composition increases,′ phase size becomes more uniform and′ phase coarsening mechanism changes from the solute diffusion mechanism to boundary migration mechanism.

Ni-based superalloy; phase-field method; precipitation kinetics;growth mechanism; kinetic exponent

(编辑 李艳红)

Project(51401118) supported by National Natural Science Fund of China; Project supported by Funding Program for Young Teachers in Universities of Shanghai, China

2016-12-08;

2017-05-08

ZHAO Yan; Tel: +86-15900915176; E-mail: zhaoyan8626@shu.edu.cn

国家自然科学基金资助项目(51401118)；上海高校青年教师培养资助计划

2016-12-08；

2017-05-08

赵彦，讲师，博士；电话：15900915176；E-mail：zhaoyan8626@shu.edu.cn

10.19476/j.ysxb.1004.0609.2018.01.14

1004-0609(2018)-01-0116-10

TG146.1

A