软刚臂单点系泊系统系泊力计算两种方法对比

，，

(武汉第二船舶设计研究所，武汉 430064)

浮式生产储油船(FPSO)以其投产快、投资低、适应水深范围广、储油能力大以及应用灵活等优势被广泛应用于浅海、深海及边际油田的开采[1]。在船舶系泊方面，目前国外系泊产品大部分采用单点系泊系统。国内共有单点系泊系统20多套，主要与FPSO配套使用。软刚臂式单点系泊系统由于结构简单，工作安全可靠，维修工作量少，环境适应性较强，便于解脱等优点，在渤海海域FPSO系泊系统中得到了广泛应用。渤海油田FPSO软刚臂单点系泊系统共计7套，其中3套是由SBM公司制造，均采用水上软刚臂结构形式[2]。

此前，有不少关于软刚臂单点系泊系统系泊力计算的研究。早期系泊力的计算都是采用CCS规范中介绍的准静态方法，即计算定常力、一阶波浪力、二阶波浪力，线性叠加得到总的系泊力。准静态系泊力计算的局限性较大，后来发展成采用单根弹簧(锚链)模拟软刚臂，保证系统刚度与实际刚度相同，计算FPSO的运动和受力[4]。单根弹簧简化模型不考虑三维结构，同样不够准确。现在一般都是建立软刚臂三维模型模拟实际系泊结构，采用时域耦合方法计算系统的受力和运动情况[5- 6]。目前还没有人比较过准静态方法和时域方法的优缺点及误差情况。

软刚臂单点系泊系统系泊性能的计算极为关键，直接影响到系泊支架、系泊刚臂以及导管架等结构件的设计，是单点系泊系统设计的基础。传统计算方法是基于准静态的频域计算，具有一定的局限性。在此情况下很有必要研究准静态方法与动态时域方法的差别、精度及适用情况等。

1 理论概述

1.1 系泊船运动

单点系泊FPSO在迎浪不规则波中的运动主要包括一阶波频运动和二阶低频纵荡运动。对于一阶波浪力，其谱密度函数可直接根据波浪谱密度函数S(ω)和波频运动传递函数|Hx(ω)|计算得到[3]

Sx(ω)=|Hx(ω)|2S(ω)

(1)

对于二阶波浪力，其谱密度函数计算公式为

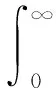
(2)

式中：SF(μ)为波漂力谱；μ为差频；S(ω)为波浪谱密度函数；T(ω+μ,ω)为波漂力幅的二次传递函数(QTF)。

平均波漂力可由波浪谱密度函数S(ω)和平均波漂力二次传递函数T(ω,ω)计算得到：

(3)

系泊船低频纵荡运动的最大值可按下式计算。

(4)

(5)

式中：σxl为低频纵荡运动标准差；C11为系统平均刚度；b为总线性化阻尼；SF(μc)为波漂力谱；Xmax,lf为低频纵荡最大偏移；N为振荡次数。

1.2 多体耦合时域运动方程

综合考虑风、浪、流以及单点系泊系统回复力的联合作用，FPSO的时域运动方程为[5- 6]

(6)

式中：M为FPSO的质量矩阵；A(∞)为最大计算频率对应的附连水质量矩阵；r(t)为辐射阻尼的脉冲响应函数矩阵，附连水质量、辐射阻尼系数均采用三维势流理论应用源汇分布方法计算得到；D为FPSO慢漂阻尼矩阵；K为FPSO静水回复力刚度矩阵；F(1,2)(t)为一阶、二阶波浪载荷；Fw(t)、Fc(t)分别为风流载荷；FSPM(t)为单点系泊系统提供的回复力。

在不规则波浪下，作用于结构物上的瞬时波浪力可以写为

F(1,2)(t)=F(1)(t)+F(2)(t)

(7)

(8)

[(ωj-ωk)t-εj-εk]}

(9)

式中：F(1)(t)为作用在FPSO上的一阶波浪力；η(τ)为海浪的随机波面升高的时域历程；h(t)为脉冲响应函数，由一阶波浪力传递函数通过傅里叶变换得到，即

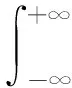
(10)

(11)

若已知整个频率范围内的fω(ω)，即可按上式求得h(t)，然后按波浪时历η(τ)，根据式(10)求得一阶波浪力。

FPSO与系泊刚臂通过位于船艏的系泊支架和系泊腿进行连接，系泊腿与系泊刚臂通过两个万向节和一个旋转接头进行连接。系泊腿作为中间结构，由于受风面积小，风载荷可以忽略，其时域运动方程为

(12)

式中：mp为系泊腿质量矩阵；Kp为考虑结构之间相互影响的12×12的耦合刚度矩阵。

1.3 风、流载荷计算

风流载荷可以根据OCIMF(Oil Company International Marine Forum)规范给出的VLCC所受风、流载荷经验公式及其模型试验所得系数进行计算[9- 10]。

风载荷计算公式为

(13)

式中：CXW、CYW、CXYW分别表示纵向风力系数、横向风力系数以及首摇风力矩系数；ρW为空气密度；VW为海平面10 m处风速；AT为艏向受风面积；AL为侧向受风面积；LBP为垂线间长。

流载荷计算公式为：

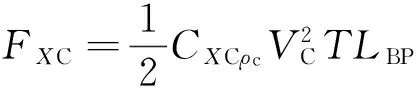
(14)

式中：CXC、CYC、CXYC分别表示纵向流力系数、横向流力系数以及艏摇流力矩系数；ρC为海水密度；VC为吃水范围内的平均流速；T为平均吃水；LBP为垂线间长。

由于三维势流理论不考虑粘性作用，只能得到附体的势流阻尼，低频运动阻尼对于单点系泊FPSO低频纵荡运动而言，至关重要[11]。本文根据BV船级社的经验公式计算低频运动阻尼[12]。

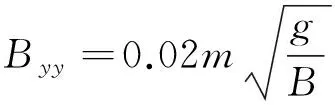
(15)

式中：Bxx为低频纵荡阻尼；Byy为低频横荡阻尼；Bφφ为低频艏摇阻尼；L为船长；B为船宽。

2 环境条件与耦合模型建立

2.1 FPSO主尺度及海洋环境条件参数

计算模型主要参数如表1所示。

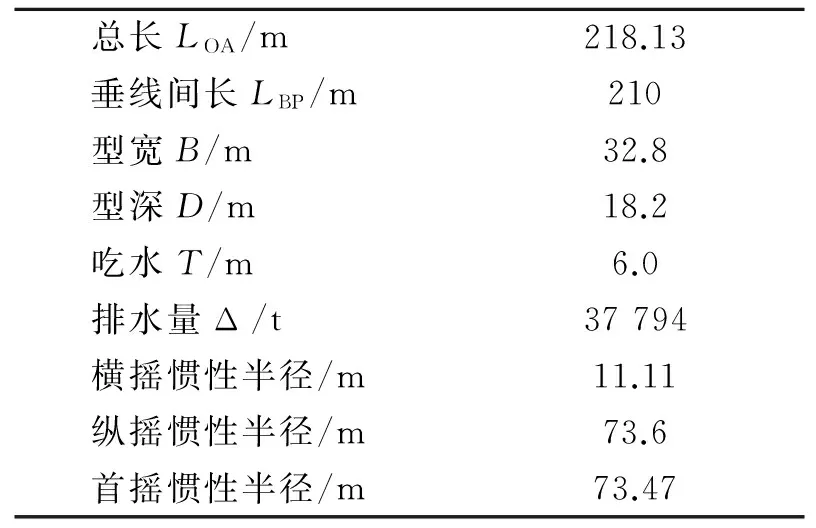
表1 FPSO主要参数

选择JONSWAP海浪谱，公式如下。

(16)

按照算例中选取的海洋环境条件(见表2)，计算可得γ=4.05。

表2 环境条件

2.2 全耦合模型建立

用Maxsurf建立FPSO三维模型，导入Workbench，在Workbench中建立软刚臂系统模型并做相关处理，把系泊支架与船艏固结在一起。系泊支架与系泊腿通过万向节连接，具有2个自由度；系泊腿与系泊刚臂通过球铰接连接，具有3个自由度；用立柱表示固定塔架，系泊刚臂与固定塔架利用球铰接连接，具有3个自由度。在划分网格时，定义船体网格尺寸为3 m，系泊腿网格尺寸为1.0 m，软刚臂网格尺寸为1.5 m，模型总网格数为9 549。FPSO及软刚臂网格模型如图1所示。坐标原点取在FPSO艉部水线面处。

图1 软刚臂单点系泊FPSO全耦合模型网格

3 系泊运动计算及结果分析

3.1 系泊运动计算方法

频域计算中，首先计算风、流载荷、平均波浪漂移力，根据这3个定常力，结合刚度曲线，计算出平均位移以及对应的平均刚度。然后计算波频位移、低频位移，根据API推荐的算法，得到FPSO总的位移；根据总位移和系统刚度曲线，计算出总的系泊力。

时域方法是通过建立多体时域耦合运动方程，迭代计算，从而得到FPSO的各自由度运动响应，与实际系泊系统比较接近，因此该方法基本可以模拟实际工况下FPSO的运动响应及单点系统的受力。

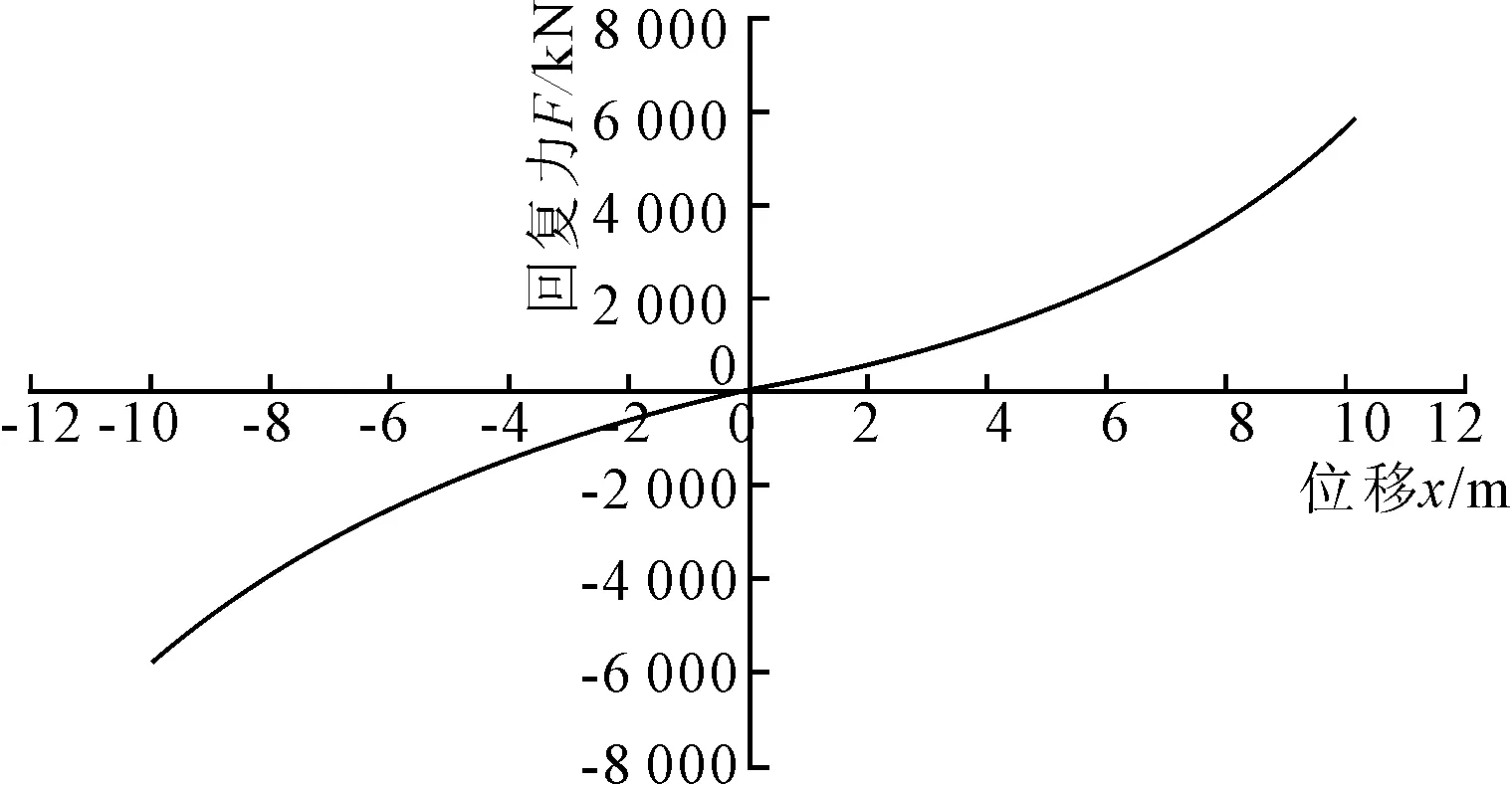
图2 系统刚度曲线

3.2 计算结果及分析

表3 频域计算结果

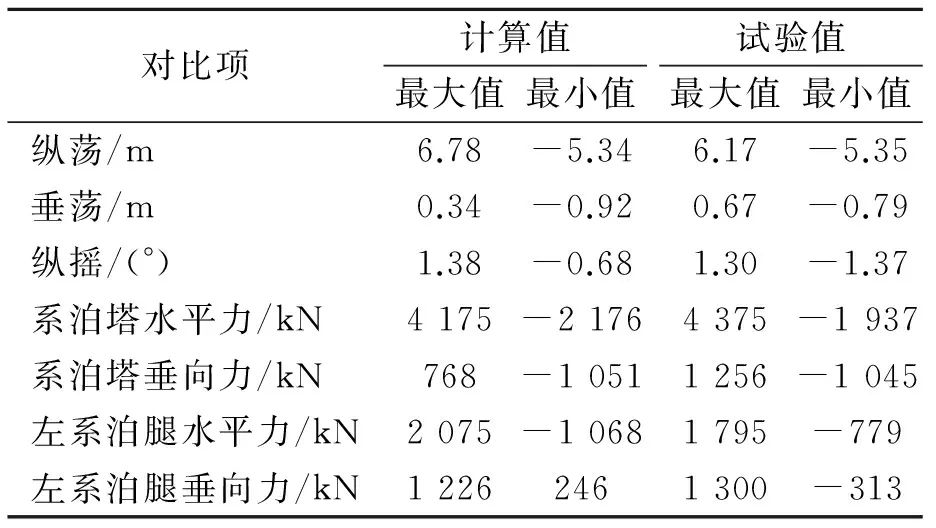
表4 时域计算结果及试验值

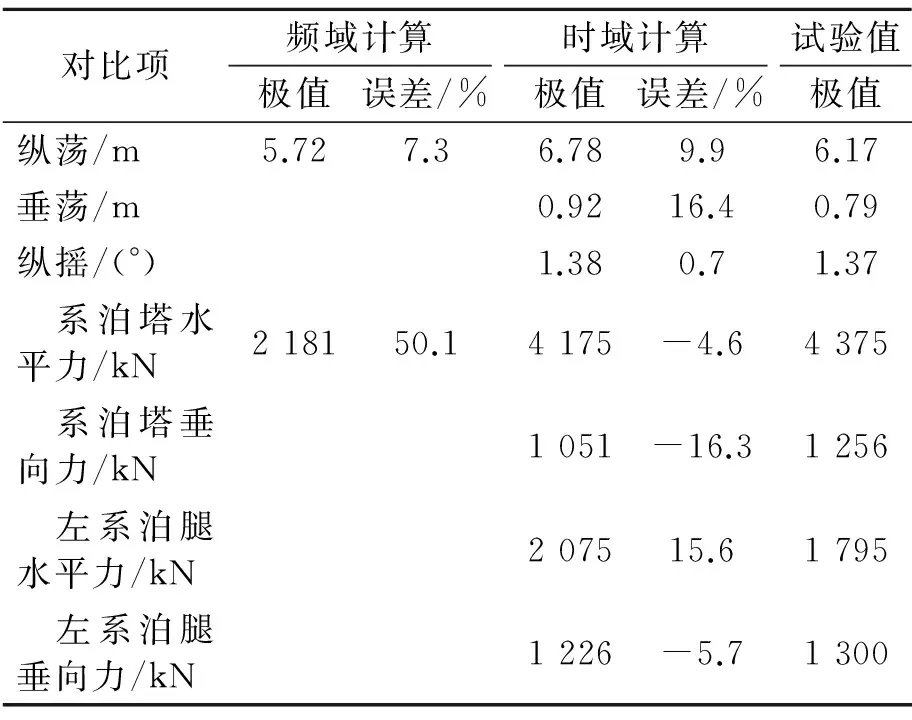
表5 计算结果误差对比

注：误差计算以实验值为基准，只关心极值大小，忽略方向。

从计算的内容来看，频域方法一般只计算风浪流同向的工况，且只能估算系统的水平系泊力，不能预报船体的六自由度运动和各关节上的受力；时域方法可以计算各种风浪流组合工况，除了系统的水平系泊力以外，还可以计算垂向系泊力及其他关节上的受力，能预报船体的六自由度运动。从计算的精度来看，频域计算的误差相对较大，时域计算的结果比较接近试验值，说明时域方法在预报软刚臂单点系泊系统系泊性能时是可行的。

从两种方法理论基础来看，频域方法是基于准静态，风、浪、流各不干扰，三者进行线性叠加，而且认为软刚臂系统对于船体的运动也几乎没有影响，采用裸船运动的频响来计算船体的运动。对于系统刚度曲线的使用，先计算定常力，再计算其对应的平均位移和平均刚度，用平均刚度来代替系统的实际刚度，显然也是有一定误差的。另外，这种方法把系统看成了二维空间的运动，没有考虑软刚臂其他自由度运动的影响，各结构惯性力的影响也被忽略了，种种原因导致了频域计算的较大误差。

时域方法建立FPSO与系泊系统的全耦合模型没有以上缺点，能更好地反应真实情况。万向节、球铰接的使用，使运动和载荷可以方便的传递，各结构之间的相互作用可以很好地模拟，最终的计算结果也表明了该方法确实可行。

系泊力计算需要与软刚臂系统设计迭代进行，首先参考母型主尺度及压载重量，得到刚度曲线，计算系泊力；根据计算结果修改软刚臂尺寸及重量，重新进行系泊力计算，不断迭代直到FPSO的位移和系统受力均满足要求。在迭代过程中，需要进行大量计算，频域方法虽然误差较大，但是使用简单，可以很快地得出结果，而时域计算则比较费时。李淑一、夏华波、刘成义等人采用时域方法进行计算，其前提是软刚臂的主尺度已经确定，才能方便地使用，如果是初次设计，软刚臂系统的主尺度没有确定时，准静态方法的优势就显示出来了。所以说准静态方法在单点系泊系统设计的初级阶段仍然具有一定的指导意义，而且计算的结果可以作为软刚臂时域耦合计算的参考。在单点系泊系统详细设计阶段，采用软刚臂时域耦合计算，可以较为准确地提供船体运动及各关节受力，为结构件设计提供输入。

通过本文的比较，不仅可以明确两种方法的差别和适用情况，还可以知道二者大概的误差范围，今后在计算过程中，考虑这部分误差，可以得到更为准确的结果，为软刚臂单点系泊系统系泊性能计算提供参考。

[1] 袁中立,李春.FPSO的现状与关键技术[J].石油工程建设,2005,31(6):24- 29.

[2] 刘斌,张晓.水上软刚臂系泊系统YOKE失效分析[J].天津科技,2014,41(1):47- 50.

[3] 刘应中,廖国平.船舶在波浪上的运动理论[M].上海：上海交通大学出版社,1987.

[4] 李欣,杨建民,范模.渤海油田浅水软刚臂系泊FPSO触底分析[J].海洋工程,2004,22(2):51- 53.

[5] 刘成义,唐友刚,李焱,等.浅水单点系泊FPSO软刚臂参数敏感性分析[J].中国舰船研究,2014,9(5):69- 76.

[6] 李淑一,王树青.基于多体分析的浅水FPSO和水下软刚臂系泊系统运动特性研究[J].中国海洋大学学报,2011,41(9):95- 102.

[7] 林青山,廖国平,李谊乐，等.潜体在不同浪向的双色波中受到的二阶慢漂力[J].上海交通大学学报,2003,34(1):1- 5.

[8] 刘滋源,廖国平,刘应中.有限水深对二阶定常波浪力的影响[J].上海交通大学学报,1996,30(10):149- 153.

[9] Oil Companies International Marine Forum.Prediction of wind and current loads onVLCC [M]. London:Wiserby&Co.Ltd.1994.

[10] 李兰霖.单点系泊系统低频运动响应研究[D].大连：大连理工大学,2013.

[11] 肖龙飞,杨建民,胡志强.极浅水单点系泊FPSO低频响应分析[J].船舶力学,2010,14(4):372- 377.

[12] 夏华波.水下软刚臂单点系泊研究[J].船海工程,2014,43(3):166- 170.