改进的基于隐马尔可夫模型的自适应IMM算法
2018-03-01张杨
张 杨
(海军航空大学,山东烟台264001)
机动目标跟踪应用广泛,且一直是目标跟踪领域的研究难点和重点。迄今为止,学者们已经提出了许多机动目标跟踪算法[1-2]。其中,交互式多模型算法(Interacting Multiple Model,IMM)[3-4]使用多个模型进行并行滤波,并将模型转移视为马尔可夫过程,通过马尔可夫概率转移矩阵和更新后的模型概率来实现模型切换,解决了单一机动模型难以准确描述目标复杂机动形式和应对未知机动的问题。这是一种具有较低费效比、次优的、结构简单的算法,因而得到了广泛的研究和应用[5-8]。
IMM算法采用固定的马尔可夫参数来描述模型的转换过程,这样存在2个限制:一是实际情况中机动目标的机动情况信息很难提前获得,当先验信息不足或不完全准确时会导致马尔可夫矩阵的设置不符合当前跟踪环境,使得跟踪精度降低;二是在经典的IMM算法中,其马尔可夫转移概率矩阵在整个跟踪过程中是固定不变的,这样使得模型转换概率在目标稳定运动和机动转换阶段是一致的,不能根据目标的状态实时调整,进而降低了跟踪精度[9-10]。
许多学者针对IMM算法的这种缺点,利用算法的各种后验信息提出了自适应马尔可夫参数的IMM算法。例如,采用构造误差压缩率的方法[11-12]、模型概率或模型似然概率对马尔可夫转移概率矩阵进行修正[13-14],取得了一定的效果。但此类方法均是利用后验信息经过简单地处理后直接对马尔可夫转移概率矩阵进行调节,容易出现算法不稳定的情况。
文献[15]采用隐马尔可夫模型(Hidden Markov Model,HMM)[16-17]替代IMM算法的马尔可夫模型,并结合Baum-Welch算法[18]实现了马尔可夫转移概率矩阵的实时估计,提高了跟踪精度。但是该文献中只对HMM链的长度和Baum-Welch算法的递推次数2个参数进行了简单设置,并未探讨其对跟踪效果的影响和明确具体的参数设置依据,从而算法存在一定的局限性。
本文在文献[15]的基础上,提出了改进的基于隐马尔可夫模型的自适应IMM算法(Improved Adaptive Imm Algorithm Based on Hidden Markov Model,IHIMM),详细分析了隐马尔科夫链长度和Baum-Welch算法迭代次数对算法性能的影响,进一步明确了其设置依据;并针对IMM模型切换误差增大问题采用2种方法进行修正。通过仿真对比分析了参数的设置和修正方法对该算法性能的影响,并与经典IMM算法对比证明了算法的有效性。
1 IMM算法中的HMM模型
本文所讨论的跟踪问题均建立在以下的混合估计系统[19]:
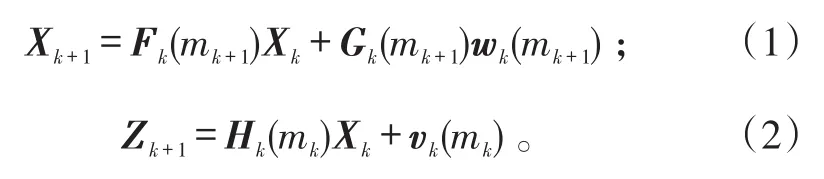
式(1)、(2)中:X和Z分别是目标的状态和量测向量;F、G、H是已知的系统的系数矩阵,根据所处的模型m而定;w、v是与系统模型相对应的、相互独立的过程和量测噪声矩阵,其噪声为加性高斯白噪声,其协方差矩阵分别为Q、R。
隐马尔可夫模型(HMM)是关于时序的概率模型,如图1所示。其主要由2个过程组成:第1个为马尔可夫链生成的不可观测的状态随机序列的过程,该过程是隐藏的;第2个为由各个状态产生可观测随机序列的过程。一个HMM模型可以用λ=(π,P,B)来进行描述,π为初始状态概率向量;P为马尔可夫转移概率矩阵,π和P一起描述了第一个过程的马尔可夫链。B=(bj(k))为观测概率矩阵,bj(k)为由状态j观测到k的概率,B描述了产生观测序列的过程。

图1 (IMM算法中的)HMM结构图Fig.1 HMM structure diagram(in the IMM algorithm)
令IMM算法的模型集有N个模型,令k时刻第i个模型表示为mk=i,模型i输出的目标量测估计为。定义3个概率:表示为k-1时刻模型i转移到模型j的概率;为k时刻模型i的概率;为由k时刻模型i输出的量测估计到量测Zk的概率。其表达式分别为:

式(3)~(5)中,Zk=[Z1,Z2,…,Zk],表示直到k时刻的量测序列。
须要指出传统HMM模型和IMM算法中的HMM模型的不同。传统的HMM模型中,每一时刻的状态(隐藏态)仅为状态集中某一状态,其观测概率矩阵B表示的为状态直接到对应观测的概率,且其参数一般是时不变的;而IMM算法中的HMM每一时刻的状态为模型集中全部模型的状态,量测概率矩阵B表示的则为每个模型通过目标量测估计作为“中介”到量测的概率,且其3个参数均是时变的。
2 Markov转移概率矩阵的实时估计
在IMM算法中,目标的量测序列显然是能直接获取的,模型概率和量测概率矩阵也能通过模型的滤波得到的后验信息计算得到(后面将有相关式子和说明)。结合上一节总结的IMM算法中的HMM,该问题可以重新描述为在已知HMMλ的观测序列、μ和B的参数的情况下,估计其马尔可夫转移概率矩阵A。因此,考虑采用HMM相关算法中的Baum-Welch算法来求解上述问题。
Baum-Welch算法是在仅有观测序列的条件下,通过EM算法来求解HMM模型的参数,是一种非监督的学习算法。给定IMM算法中的HMM的量测序列,在描述 Baum-Welch算法的基本过程之前,先定义概率函数:
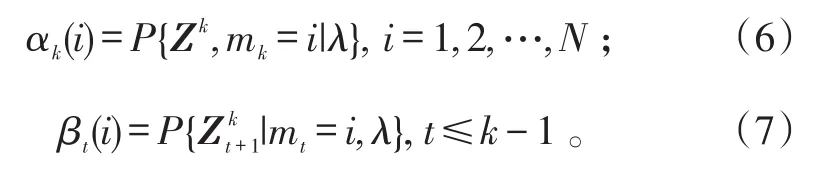
式(6)、(7)中:αk(i)为Zk中k时刻模型为i的前向概率;βt(i)为中t时刻模型为i的后向概率。

在IMM算法中,模型概率μ可以从其迭代过程直接获得。同时,IMM算法中,其模型的似然函数定义为:

由于有
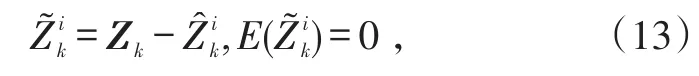
结合式(12),则有:
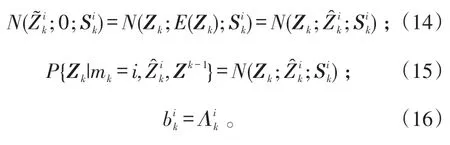

令γt(i)为在Zk中t时刻模型为i的概率;ξt(i,j)为在Zk中t时刻模型为i且下一时刻模型为j的概率,则有:

根据式(6)、(7)有:
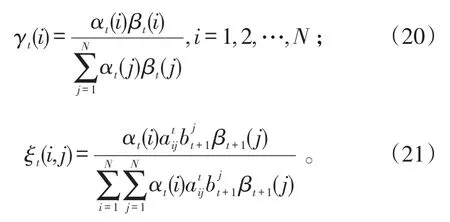
根据文献[18]中对Baum-Welch算法过程的描述,令初始状态的HMM为λ(0)=(μ(0),A(0),B(0)),迭代的步数为n=1,2,…,量测序列为Zk,则马尔可夫转移概率矩阵的迭代式为:
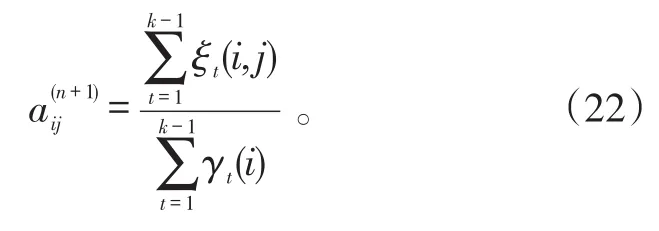
须要强调的是,在Baum-Welch算法中μ和B都是须要迭代计算的,而在IMM算法中的HMM,其μ和B都能通过后验信息计算而来,故不通过迭代计算。

根据Baum-Welch算法的原理,在迭代过程会使得算法最终收敛,学习出最接近所给量测序列的真实HMM参数的估计值。
在这里,将上述估计马尔可夫转移概率矩阵的过程,即式(6)~(23),结合到文献[20]中的IMM算法的迭代过程中,构成了基于HMM的自适应IMM算法(HIMM),使得算法能根据目标的历史量测和后验信息,实时更新得到适合于当前目标状态的马尔可夫转移概率矩阵,从而提高跟踪精度。
3 HIMM的参数设置及算法修正
上一节中,对HIMM算法中的马尔可夫转移概率矩阵的实时估计过程进行了详细的描述。而其中HIMM的参数:HMM中的隐马尔可夫链的长度、Baum-Welch算法的迭代次数等的设置对算法的性能是存在影响的。同时,HIMM算法的局限性也需要分析,使其能更好地应用于实际。下面就这2个方面进行详细分析与说明。
3.1 HIMM的参数设置问题
首先是隐马尔可夫链的长度问题。通常,HMM是从t=1 s时刻进行建立,且经历时间越长(链越长),其积累的历史信息越多,学习估计得到的HMM参数越准确。但是在目标的跟踪过程中,一般情况下目标的非相邻的机动过程相关程度很小,如果建立的HMM链过长,包含了几段不同的机动过程,会导致目标在估计当前时刻的马尔可夫转移概率矩阵时,受无关的历史信息干扰,影响估计效果,且计算量会随链的长度增加;而建立的隐马尔可夫链太短时,虽然计算量小,则会因为舍弃了部分有用历史信息使得HMM对目标后验信息的变化过于敏感,影响估计效果。因此,HMM链的长度是影响A的参数之一,须要根据实际设定,像文献[15]那样将整个轨迹作为一条隐马尔可夫显然是不合理的。令HMM链的长度为l,考虑采用时间窗的方式直接提取相应长度的量测序列:则当前时刻为k,长度为l的量测序列为

则每个时刻估计A时,都在时间窗提取的量测序列Zl,k内重新构建HMM链。
其次是关于Baum-Welch算法的迭代次数的问题。根据式(22)可以看到,其迭代的次数代表了调节的程度,迭代次数越多,马尔可夫转移概率矩阵受调节的程度越大。虽然这样会使得匹配或优势模型的概率提高而提高跟踪精度,但是也会增大计算负担。同时当模型稳定时,A中转移到匹配或优势模型的概率会不断增大并接近于1,如果迭代次数较大时,会加速这一调节过程,而在计算机中数据的长度是有限的,当概率很接近1或0时,计算机的位数限制会使其进行四舍五入,导致容易出现向匹配或优势模型转移的概率为1,其他的为0的情况,破坏了IMM算法的结构,影响跟踪效果,因此迭代次数不能太大。仿真中发现,迭代次数在小于4~5次为宜。在文献[15]中Baum-Welch算法只进行了一次迭代,显然是不能满足需求的。
3.2 HIMM的局限性及修正
通过分析和仿真总结出了HIMM算法的局限性:降低了在目标发生机动转换时的模型切换速度,增加了峰值误差。结合算法过程及实际仿真数据,分析出以下2个原因:一是由于马尔可夫矩阵的自适应调节,使得向匹配或优势模型的转移概率和模型概率增大,这样使得这(几个)模型的“惯性”增大,从而其需要调节的程度加大、时间增长,误差随之增大;二是由于同一模型稳定时间太长或调节速度过快,使得向非匹配或劣势模型的转移概率和模型概率接近于0,导致机动信息在上述模型的似然函数上体现不明显,影响了模型转换过程。
因此,针对以上分析,提出了如下2个修正措施。
一是机动检测法。前面已经分析过了,Markov转移概率的自适应调节,使得IMM模型的“惯性”增大。通过机动检测,强制使算法在目标进行机动变化时初始化Markov转移概率矩阵,一定程度上减少模型“惯性”带来的机动切换期间的峰值误差。
由于IMM算法中模型的似然函数从一定程度上反映了滤波误差的大小,所以定义以下似然函数比和检测式:

式(25)成立时,即认为目标发生了机动。κ的设置根据具体跟踪环境和噪声水平而定,过大或过小则会造成漏警或虚警,实验中得到的经验值为15~2.5。当检测到目标正在进行机动时,由于HMM调节能力很强,因而直接将当前马尔可夫转移矩阵设置为初始值A0,然后根据IMM的模型概率计算方法直接计算当前初始化的模型概率。令,则k模型的概率初始化为:

这样,在机动检测正确的前提下,就能将调节增大的惯性减小,从而减小切换时间和跟踪误差。当机动检测不正确时,会使得算法的Markov转移概率矩阵初始化的时机错误,从而影响跟踪效果,因此机动检测的门限需要实际中多次实验确定,保证机动检测的正确。
二是概率钳制法。根据第2种原因的分析,直接将马尔可夫转移概率矩阵的元素和模型概率的取值“钳制”在某一范围,使得非匹配或劣势模型的概率不至于过小而影响似然函数对误差的传递。当转移概率或模型概率到达某一上限时,这2种概率不更新,等于上一时刻的值。
根据上述分析,将新的隐马尔可夫链的长度和Baum-Welch算法的迭代次数的2个参数设置依据和2种修正方法应用于HIMM中,即得到IHIMM算法。
4 实验仿真与分析
为了检验并分析IHIMM算法的性能,下面对该算法进行仿真分析,并设置不同参数进行对比。

根据上述设定的仿真环境,采用Matlab R2014a进行编程仿真,做100次蒙特卡洛仿真,采用均方根误差(Root-mean Square Error,RMSE)[23]作为评价标准,仿真分为2部分,分别为HIMM算法参数设置对性能的影响和与经典IMM算法的跟踪效果对比。
4.1 参数对IHIMM算法的影响
定义以下IHIMM的默认设置:采用的IHIMM算法的时间窗长度设置为8 s,迭代次数设置为2次,并进行机动检测和概率钳制修正,机动检测的门限设置为2,马尔可夫转移概率和模型概率的上限分别钳制在0.098 5、0.95。在后续的仿真中,除了特殊说明的参数外,其余参数均按照以上默认的进行设置。
将未修正的IHIMM、只进行机动检测修正、进行机动检测和概率钳制的IHIMM跟踪效果仿真对比如图2所示。

图2 不同修正情况下的IHIMM性能对比Fig.2 Comparison of IHIMM performance under different correction
将IHIMM修正时的机动检测门限κ分别设置为1.5、2、6进行仿真,其结果对比如图3所示。
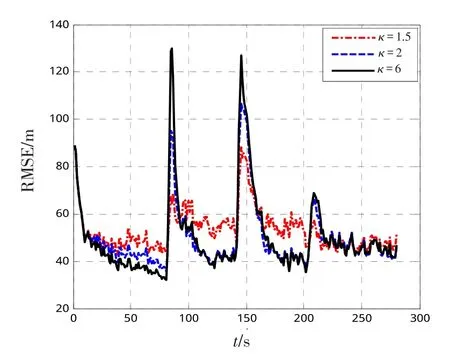
图3 不同机动检测门限的IHIMM性能对比Fig.3 Comparison of IHIMM performance of different maneuver detection thresholds
将IHIMM的Baum-Welch算法的迭代次数n分别设置为1、2、4,将仿真结果对比如图4所示。
将IHIMM的时间窗长度l分别设置为3 s、8 s、16 s,仿真结果对比如图5所示。

图4 不同迭代次数下的IHIMM性能对比Fig.4 Comparison of IHIMM performance under different number of iterations
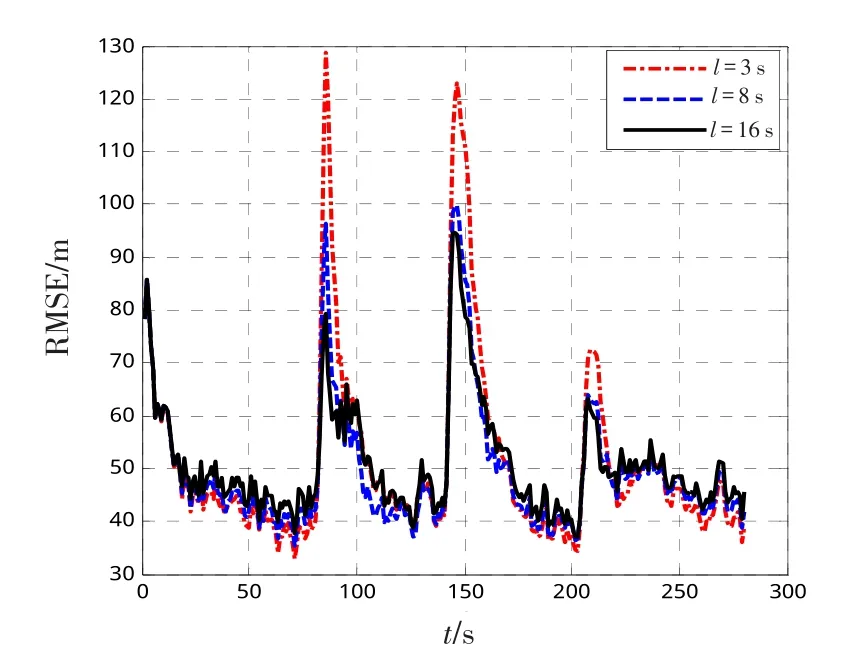
图5 不同时间窗长度下的IHIMM性能对比Fig.5 Comparison of IHIMM performance under different time window lengths
根据图2~5,结合目标的真实轨迹,和IHIMM算法的原理,可以分析得出:
图2的3条曲线的3处峰值误差可看出,经机动检测和概率钳制后的IHIMM算法在模型转换时的跟踪误差能得到大幅度减小。同时,算法稳定的时间大幅度减小。因此,这2种修正方法能有效减少IHIMM在目标机动转换时的跟踪误差,加快模型切换速度。同时,可以看到在算法稳定的时候,修正后的IHIMM算法牺牲了少量的跟踪精度(200~250 s处较为明显)。
图3中可以看出,机动检测门限得适度,过小会造成虚警,使得在非机动转换时刻启动初始化机制,降低模型稳定时跟踪精度,如图中κ=1.5的曲线的100~140 s部分;而门限过大会导致漏警,使得调节机制无法及时启动,增大了模型切换时刻的跟踪误差,如κ=2和κ=6的曲线在90 s和145 s处的RMSE对比。
从图4中可以看到,迭代次数变少,模型切换处的峰值误差会变小,模型稳定处的跟踪误差会变大。这是由于迭代次数越多,调节深度越深,但模型切换时惯性越大,切换所需要调节的程度越大造成的,一般不超过4~5次。
从图5中看到,HMM采用的时间窗增长时,其模型切换时的峰值误差减小,而模型稳定时的误差增大。这是由于时间窗越短,则HMM获取的信息越少,对IMM的后验信息变化越敏感造成的。
4.2 IHIMM与经典IMM算法对比
为了验证IHIMM的算法的有效性,将其与经典的IMM算法进行跟踪效果的对比。关于IMM的模型等设置前面已说明,IHIMM的参数按照上一节定义的默认参数进行设置。仿真场景及参数采用第4节刚开始描述的场景。进行仿真,可以得到真实轨迹、量测轨迹、IMM算法估计轨迹和IHIMM算法估计轨迹对比结果如图6所示。

图6 IMM和IHIMM估计轨迹对比Fig.6 Estimated trajectory comparison of IMM and HIMM
由于目标轨迹的原因,图6的仿真结果不太明显,将其跟踪较为关键的部分进行放大显示,如图7所示。

图7 IMM和IHIMM估计轨迹对比(放大后)Fig.7 Estimated trajectorycomparison(enlarged)of IMM and HIMM
然后,进行100次蒙特卡罗仿真,得到了IMM和IHIMM的跟踪RMSE对比图如图8所示。
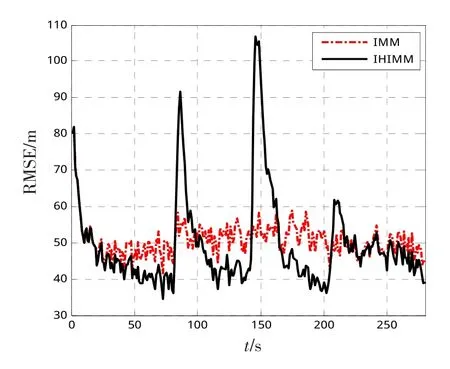
图8 IMM和IHIMM跟踪性能对比Fig.8 Tracking performance comparison of IMM and HIMM
为了更好地对比2种算法的性能和充分反映算法的性能,提取某次的仿真,将2种算法的模型概率变化在图9进行对比,同时将IHIMM的马尔可夫转移概率矩阵的对角线的值的变化如图10所示。

图9 IMM和IHIMM概率变化Fig.9 Probability changes between IMM and IHIMM
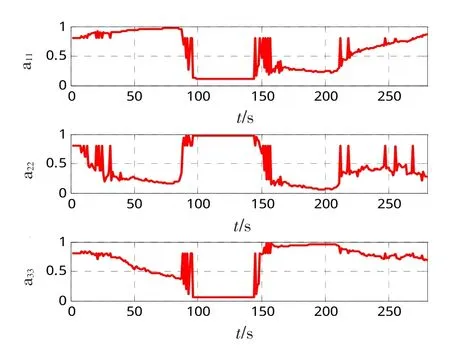
图10 IHIMM的Markov转移概率变化情况Fig.10 Markov transition probability change of IHIMM
其中,模型1为匀速模型,模型2和3分别为转弯率分别为 9(°)/s和 -3(°)/s的匀速转弯模型。a11,a22,a33分别为马尔可夫转移概率矩阵对角线的第1、2、3行值。
根据图7、8,结合目标的真实运动情况,可以看到,IHIMM算法较之IMM算法,能够在目标稳定的时候,提高目标的跟踪精度,在本文采用的仿真场景下,IHIMM较之IMM的跟踪RMSE提高了约10 m。但是,由于调节,使得目标在概率稳定期间优势模式概率增大,从而增加了该模型的“惯性”,使得IHIMM算法在机动转换期间峰值误差较大,最大的峰值RMSE误差为108 m。因此,IHIMM算法能有效提高目标在非机动切换期间的跟踪精度。
从图9的2种算法模型概率对比以及图10的IHIMM算法的Markov转移概率矩阵的对角线值的变化,能够看到,IHIMM算法能够在目标模型稳定的时候,自适应调节其马尔可夫转移概率矩阵,提高向匹配或优势模型转移的概率,进而提高相应模型的概率,使模型概率得到了“平滑”,进而增加了模型概率的稳定性(如图9、10的100~140 s的时段),减少了非匹配或劣势模型的竞争,从而提高了跟踪精度。IHIMM跟踪的RMSE在模型稳定的时段,较之IMM平均减小了约10 m。在目标进行机动转换时,IHIMM算法要进行模型转换,但由于模型稳定时的调节,使得模型的概率对比更加明显,从而提高了模型滤波的惯性,使得转换的幅度需求变大,时间变长,从而使得误差增大。从图9中可以看出,IHIMM算法在本次仿真中模型切换需要约10~15 s的时间。
综上,IHIMM算法能显著提高IMM算法在模型稳定时的跟踪精度和稳定性,但会增加目标机动切换时的模型切换时间,并提高峰值误差。因此,本文提出的IHIMM算法适合机动较少,运动较为稳定的目标,如运输机、民航客机、水面舰艇等。
5 结论
本文提出了基于HMM的自适应IMM算法,并进行了修正,分析了不同参数设置对该算法的跟踪效果的影响,并进行了仿真验证。同时,通过将该算法与经典的IMM算法进行仿真对比,证明了本文提出的IHIMM算法能显著提高目标在机动切换时的跟踪精度和稳定性。但存在机动切换时需要时间增长和误差增大的问题,计划在后续的工作中进行改进完善。
