平面近场测试中探头位置误差的分析

刘 镝

（91404部队，河北秦皇岛066001）

平面近场测量中，探头沿着在z=d的平面上沿着水平和垂直方向进行栅格采样[1-3]。理想情况下，即探头没有位置误差时，所有采样点都在一个平面上，且所有扫描线是完全垂直和水平的[4-6]。但实际中，因为机械精度的限制，无法做到在严格的栅格点上进行采样，那么在计算远场方向图[7]时，位置误差会破坏近远场变换中的傅里叶变换等间距取点的规则，从而引入远场方向图的误差[8-11]。所以，对探头位置误差的分析对了解平面近场测试中的误差是十分重要的。

文献[12-13]对探头位置误差进行了一定的分析。但是，文献[12]主要给出了位置误差对远场参数影响的公式，未具体分析位置误差对远场方向图影响的量级；文献[13]对位置误差进行了仿真分析，但在进行误差分析时基于单个副瓣进行分析，考虑的因素有限，会导致分析结果的精度不高。本文则从论证和仿真2个角度对位置误差进行了分析，并且在仿真分析中采用全角度分析方法[14-15]，详细评估了位置误差对-50dB副瓣影响的不确定度，因为考虑了所有角域内副瓣的影响，结果更加精确，为平面近场测试中误差的分析提供了一定的依据。

1 探头位置误差引入的远场误差上界

根据平面近场测量的基本理论，在有位置误差的情况下，探头输出的是位置(p+Δp,d+Δd)处的电场，所以横向电场在(p,d)处的近场测量误差ΔEt(p,d)可用下式表示[16]：

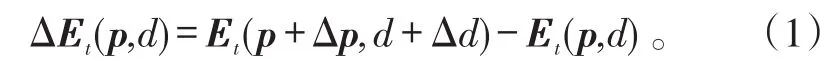
式（1）中：Et为扫描面位置(p+Δp,d+Δd)的横向电场近场分布；Et为扫描面位置(p,d)的横向电场近场分布。

在和模式工作状态下，待测天线轴向附近区域R≈0，θ≈0，且取样面上近似等于天线口径面部分的近场相位分布变化不剧烈，继续推导，可得到z位置误差造成的远场误差公式为[17]：

式（2）中：k是波数；f是频率；Δz是z向位置误差。

从式（2）中可以看出：

1）在平面近场无横向误差的情况下，z向位置误差ε0(Δz)与z向采样位置误差Δz的2次方成正比；

2）在Δz一定的情况下，测量频率f越高，ε0(Δz)越大。

同样的推导过程，得到横向位置误差造成的远场误差公式为：

式（3）中：α为锥削因子；A为待测天线口径面的几何尺寸；ΔPmax为横向x位置误差；δmax为纵向z位置误差；L0max为天线的最大尺寸。

2 探头位置误差的仿真分析

上面给出了位置误差对远场的误差表达式，下面利用计算机仿真的方式对其进行分析。

2.1 计算机模型的建立

如图1所示，在坐标系xoz中，x轴上排列着n个无限长电流丝，电流丝之间的间隔为Δs，近场采样面到电流丝之间距离为d，采样点数为m，采样间隔为Δx。假设直线阵上电流分布为-50dB副瓣切比雪夫分布。计算机仿真过程如下：

1）计算得到距离d处的近场，由近场数据通过近远场变换得到理论远场方向图；

2）引入不同类型的位置误差，由近场数据通过近远场变换得到引入位置误差后的远场方向图；

3）将理论远场方向图与引入位置误差后的远场方向图进行比较，得到误差曲线，对误差曲线进行分析计算，得到位置误差对方向图副瓣影响的量级。

图1 仿真示意图Fig.1 Schematic diagram of simulation

值得一提的是，目前国内在误差的具体分析中一般只考虑单个副瓣的影响。而实际中，误差对方向图的影响是全角域的，只对单个副瓣进行分析，必定有一定的局限性，从而影响评估结果的可靠性与准确性。

在这里采用全域分析方法对方向图所有点的ESS/SIG（即误差信号比）来取均方根（RMS）。然后根据RMS算出副瓣的不确定度[18]：

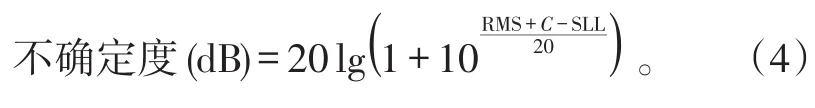
式（4）中：SLL为所要分析的副瓣电平（dB）；C=0。

2.2 计算结果及讨论

下面假定3种位置误差的分布类型。

1）假定x方向位置误差和z方向位置误差为正态分布，且均值为零、方差为σx，且有σx=σz=0.01λ。图2给出了引入位置误差后的远场方向图与理论远场方向图的对比及误差曲线。通过对误差曲线的计算，得到RMS值为-43.12dB，其对-50dB副瓣的不确定度为10.13dB。

2）假定x方向位置误差和z方向位置误差均为随机误差，且大小Δx0=Δz0=0.01λ。图3给出了引入位置误差后的远场方向图与理论远场方向图的对比及误差曲线。通过对误差曲线的计算，得到RMS值为-42.63dB，其对-50dB副瓣的不确定度为10.47dB。

图3 远场方向图的比较2Fig.3 Comparison 2 of far-fieldpattern

3）为模拟实际测试中的情况，依据某大型微波暗室实测的位置误差精度，在这里假定x方向位置误差服从均值为零、均方差为σx的正态分布；z方向位置误差服从均值为0、均方差为σz的正态分布，且σx=0.57mm=0.006λ，σz=0.22mm=0.003λ。图4给出了引入位置误差后的远场方向图与理论远场方向图的对比，通过对误差曲线的计算，得到RMS值为-57.46dB，其对-50dB副瓣的不确定度为3.07dB。

图4 远场方向图的比较3Fig.4 Comparison 3 of far-fieldpattern3

3 结论

文章首先对平面近场测试中探头位置误差对远场方向图影响的公式进行了论证分析；然后，通过计算机建模的方式对不同分布类型位置误差对副瓣的影响进行了分析。研究结果表明，位置误差对副瓣的影响很大，必须控制在零点几个毫米以内。所以在暗室的建造中，严格控制采样架探头的位置精度是十分必要的。本文对误差的分析首次使用全域分析的方式，且模拟了实际中位置误差的情况，这为后续暗室误差分析、误差补偿方法的研究提供了一定的理论依据。