基于边界速度的城市路网承载力估计方法

张 彭，孙建平，雷方舒，全宇翔，朱广宇

（1.交通运输部规划研究院 信息所，北京100028；2.北京交通发展研究院 智能交通所，北京 100073；3.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京 100044）

0 引言

路网承载力指城市道路网所能提供的最大的运输服务能力，是城市发展的约束性条件。对于拥堵日益严重的大城市，路网承载力是政策制定、城市规划调整的基本依据，越来越受到关注。目前不同的应用领域对路网承载力有不同的定义。

第一种定义为单位时间内路网所能支持的最大机动车出行量或网络流量（单位：辆/h），主要用于衡量区域土地可开发强度，优化城市空间布局及调整交通规划[1]。现有求解方法包括：①时空消耗法，用路网总的时空资源除以单次出行占用的资源量获得所能容纳的出行数[2]，又可分为一维模型[3]和二维模型[4-5]；②线性规划法，将路段容量作为约束条件，用凸优化的方法求出路网最大流量[6]，又可分为给定弧容量求解最大流[7]、固定路由求解最大流[8]、二次规划法[9-10]、过饱和模型等[11]；③割集法，寻找网络图上从起点到终点的最短路径，用最大流等于最小割容量定理求解[12]；④交通分配模拟法，通过不断增加出行量使部分路段流量达到饱和，删去饱和路段直至路网不再保持联通时获得对应的流量[13]，在其基础上又发展出启发式搜索法[14]；⑤双层优化法，从交通需求生成的角度，通过求取路段通行能力与过境交通量之差，再进行OD反推剩余交通生成量获得[15]。最新的研究成果引入了基于路由选择动态分配的模型[16]，从混合智能的角度考虑了出行可靠性因素[17]以及需求分布特征变化不确定性因素对估计结果的影响[18-19]。

第二种定义为单位时间路网所能完成的最大行驶量（单位：辆·km/h），根据饱和交通流条件下车头间距、车速计算获得[20-21]，主要用于路网运行状态、效率及效益评价。

第三种定义为城市所能支持的最大机动车保有量（单位：辆），通过将其与出行空间及时间分布特征、日出车比例等参数共同代入宏观路网模型，仿真路网运行逼近临界状态时的对应值获得[22]，主要用于需求管理及交通节能减排。

第四种定义为路网所能承载的最大在途车辆数或同时共存的出行数量（单位：辆），主要用于动静态交通一体化及排放监测等领域。宏观基本图法（Macroscopic Fundamental Diagram,MFD）[23]有助于该问题的求解，但在严重拥堵情况下，车辆密度与流量、速度的关系丧失鲁棒性[24]，影响了MFD在车辆数逼近极限情况下的适用性。

前两种定义主要是从出行量和运行效率的角度估计路网运行的极限状态，后两种更侧重于静态的承载力。针对第四种定义中求解遇到的困难，本文利用来自于社会车辆的浮动车大数据，建立能够描述路网不同状态下车辆统计特征的宏观动态仿真模型，推算极限状态下路网中行驶车辆速度的概率分布，进而在道路里程约束下对路网承载力进行求解。本文所提出的方法使用大数据标定模型参数，仿真效率高，适用范围广，更符合实际情况，有效地解决了不同规模及类型路网的承载力估计问题。

1 路网边界速度

图1为根据车辆出行时间计算在途车辆数的示意图。其中，每条实线代表一次机动车出行（Trip），实线两端分别对应行程的起止时间。

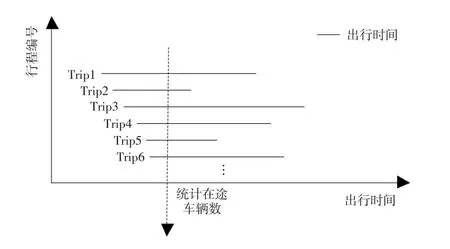
图1 在途车辆数计算示意图

在纵轴方向进行统计可得任意时刻同时在网行驶的车辆数。周期性统计在途车辆数及对应的路网均速，并将其分别作为横纵坐标可得二者关系的散点图。以2016年5月30日北京市私人小汽车的浮动车数据为例，在途车辆数与路网均速关系如图2所示，其中计算周期为5min。

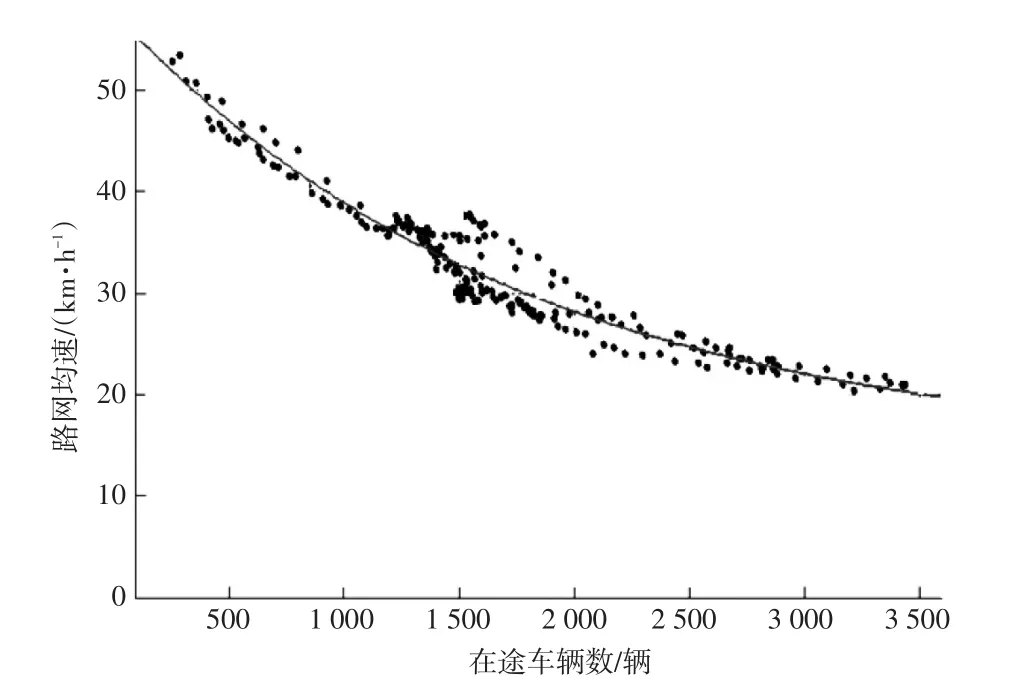
图2 在途车辆数与路网均速关系图

对图2中的散点进行拟合，拟合曲线的函数设为h(r)，即：

式中：̂为路网均速；r为在途车辆数。

采用指数函数对h(r)进行拟合，得：

式中：a,b,c为待求参数。

由式（2）可看出，当x→∞时，h(x)→c。c代表随着在途车辆数增加路网均速逐渐降低所逼近的理论边界值。城市路网由大量相互关联的路段组成，拥堵以点段的形态出现。拥堵越严重、堵点越多，则堵点上下游的状态差异越大。堵点下游始终有一部分车辆处于快速行驶的状态，从而决定了随着车辆增加，路网均速降低但不趋于零，而将收敛于某一边界速度，其对应于最大路网容量。路网处于最大容量状态时，绝大部分新入网车辆将在出发地附近遭遇严重拥堵，难以进入路网。边界速度的存在也是城市拥堵区别于城际公路拥堵的典型特征。

2 边界速度对应的路网车辆速度分布

2.1 路网中车辆速度分布

路网中车辆的行驶速度呈一定的概率分布。以北京市为例，图3给出了2016年5月30日全天不同时刻在途车辆的速度分布，分别对应于早上05：00自由流、08：00早高峰、12：00午平峰及17：30晚高峰等四种情况。从图中可以看出，自由流条件下速度—密度丧失单调对应关系，早上05：00的车速分布较不规则。除此之外，拥堵和平峰状态下车速分布均服从偏高斯分布，不失一般性假设其服从对数正态分布v～ln(μ,σ2)。以5min为周期，对连续一周工作日早晚高峰4h共49个时刻对应的分布参数分别进行最大似然估计，然后做χ2检验，自由度为10，显著性水平为0.05，接受假设比例为89.8%。在途车辆数逼近路网容量时对应的交通状态比日常拥堵状态更严重，车头间距更小，速度—密度将保持更强的单调性，故网络边界速度下车速将更加严格服从假设分布。

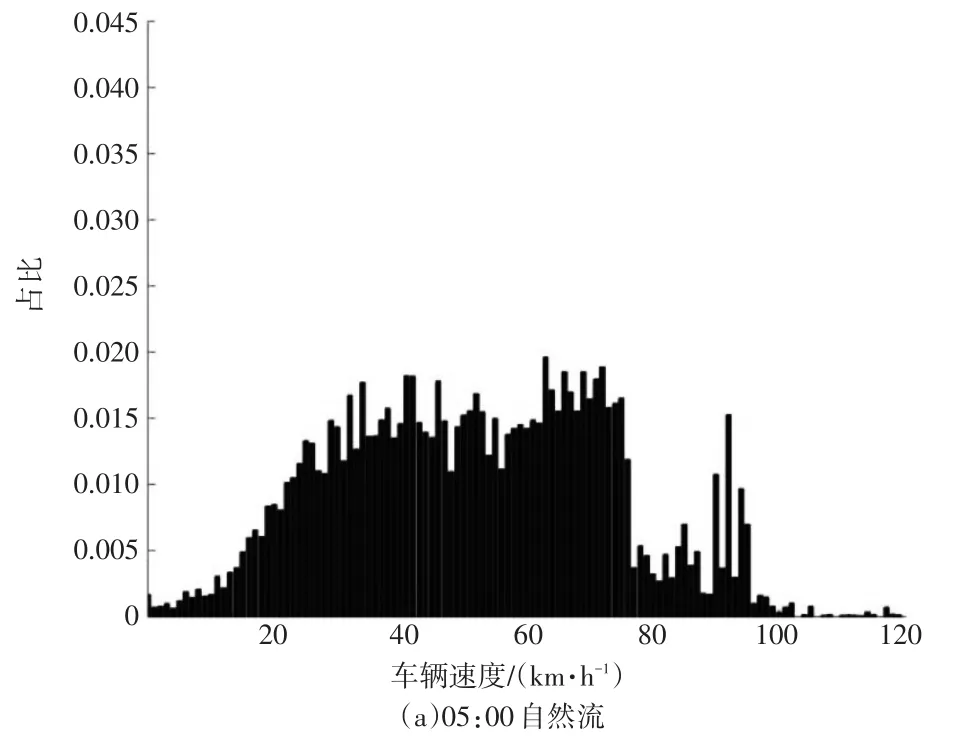
速度连续变化，将路网均速从小到大离散化为多个连续等间隔且互不重叠的速度区间，每个区间对应一个样本集，同一样本集中的样本对应相同的路网均速v̂。周期性计算路网均速，当其处于某一区间时，将此时路网中车辆速度样本放入该区间对应的样本集。如此，将所有历史样本数据放入不同速度区间对应的样本集。设定速度统计周期为15min，速度区间为2km/h，范围从4km/h到路网自由流速度。认为每个样本集中的车速样本服从对数正态分布ln(μ,σ2)，对参数μ和σ2进行最大似然估计，得：

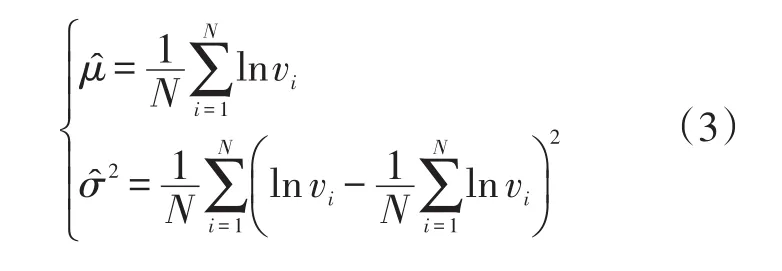
式中：μ为服从正态分布的随机变量的均值；σ2为服从正态分布的随机变量的方差；N为样本集中的样本数；vi为第i个速度样本。

2.2 车速分布参数随路网均速变化的模型

根据实际观测数据绘制散点图及拟合曲线图，如图4所示。

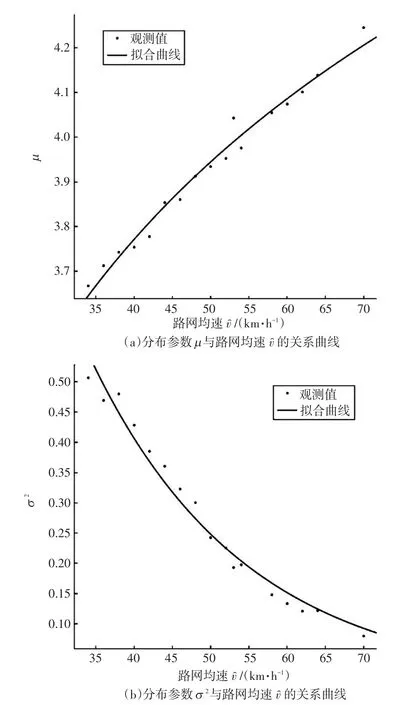
图4 车速分布参数随路网均速变化的曲线

从图4可以看出，μ与̂呈单调递增关系，σ2与̂呈单调递减关系，分别对其进行最小二乘拟合。

（1）μ与

当̂→0 时，̂=E(l nv) →-∞ ；当̂=1时，；当时，。

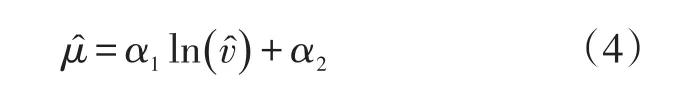
式中：α1,α2为待求参数。

（2）σ2与

当̂→ 0 时 ，=var(lnv)→∞ ；当̂→1时，=var(lnv)趋于某一正常数；当̂→∞时，

选取指数函数进行拟合，得：

式中：α3,α4为待求参数。

根据图4及式（4）、式（5）可得：α1=0.776,α2=0.910,α3=2.921,α4=-0.049。

将向量u=(α1,α2,α3,α4)定义为路网车速分布

选取对数函数进行拟合，得：特征向量，其反映了车速分布随路网均速变化的规律。表1给出了北京市中心城区快速路，主干路，次干路、支路三个不同等级路网的u值。

表1 北京市不同等级道路路网车速分布特征向量

2.3 路网边界速度对应的车辆速度分布

根据特征向量u可建立路网均速v̂与速度分布参数μ和σ2的连续函数。将式（2）中的边界速度c代入式（4）及式（5）可得对应的车辆速度分布参数，进而获得对应的车辆速度分布。

以北京市为例，按上述方法计算得出中心城区各等级路网边界速度对应的车辆速度分布参数，如表2所示。

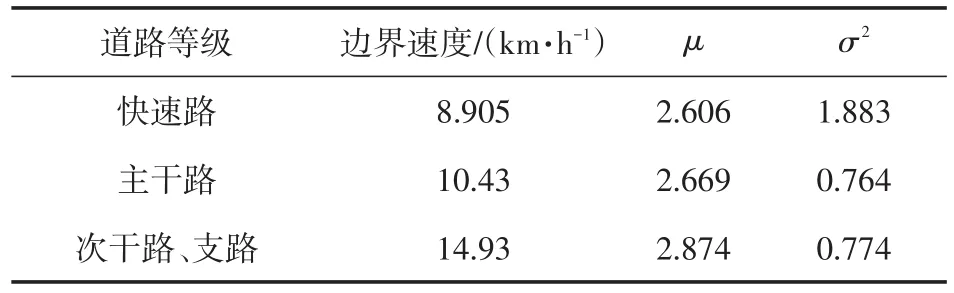
表2 北京市中心城区各等级路网边界速度对应的车速分布参数

3 路网承载力估计

3.1 车速分布与车流密度的匹配

令v̂=c，将式（2）获得的c值代入式（4）及式（5），计算路网边界速度条件下的车速分布参数，进而获得对应的车速分布。车速分布中不同速度的车辆对应不同的车头间距，具有相同车头间距车辆的数量与车头间距的乘积等于具有相同速度的车辆占用道路长度之和，边界条件下各种速度车辆占用道路长度之和等于车道数加权的道路里程。将速度从零到自由流离散化为M个区间，认为每个区间内的车辆保持近似的速度—密度关系，则车辆数与路网总长度满足以下约束条件：

式中：L为车道数加权后的道路总长度；q为待求路网可容纳的最大车辆数，即路网承载力；pi为车速处于第i个区间的车辆数在车辆总数中的占比，由车速分布在各区间积分获得；li为车速处于第i个区间时的车头间距，li=1ri，ri为对应的车辆密度，由速度—密度关系获得。

路网承载力可由式（7）获得：

用式（7）计算各等级路网的承载力qj（j=1,2,…,K，K为道路等级数），则路网总承载力等于各等级路网承载力之和，即：

式中：qc为路网总承载力。

3.2 计算流程

城市路网承载力的计算流程如图5所示。

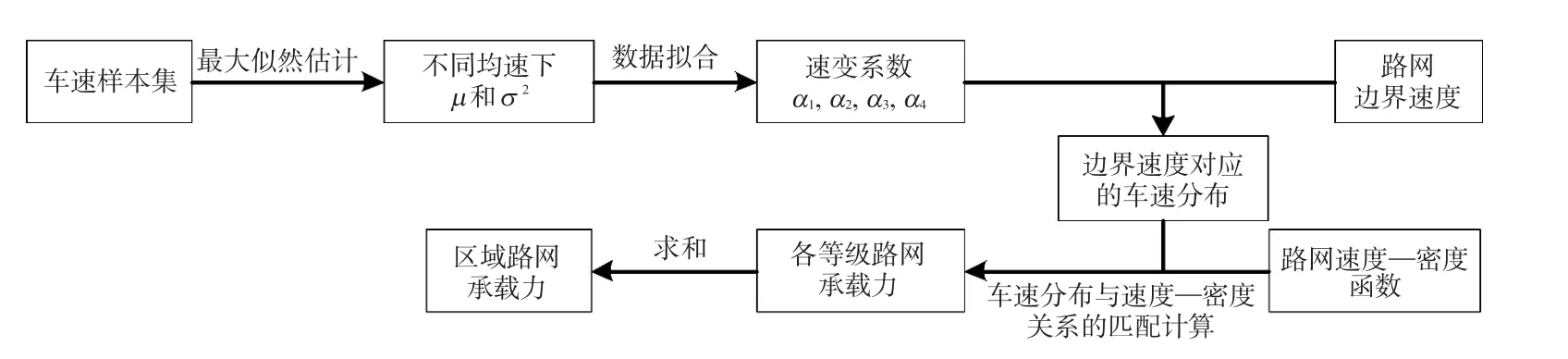
图5 城市路网承载力计算流程图

4 计算结果

本文中的数据来自北京市1.2万辆私人小汽车，通过将无线传输设备与车辆的CAN总线连接，对车辆点火熄火时间、GPS位置、油耗等数据进行实时采集。数据空间范围为北京市中心城区1 368km2，路段数40 419；时间范围为2016年5月；仿真工具为SQL和Matlab。

本文采用以实际数据标定的北京市各等级道路的速度—密度关系[25]，如式（9）所示：

式中：ρ为车流密度；ρm为流量最大时对应的车流密度；vf为自由流速度。

各等级道路速度—密度模型参数如表3所示。车道加权里程如表4所示。其中，pcu为标准车当量数。

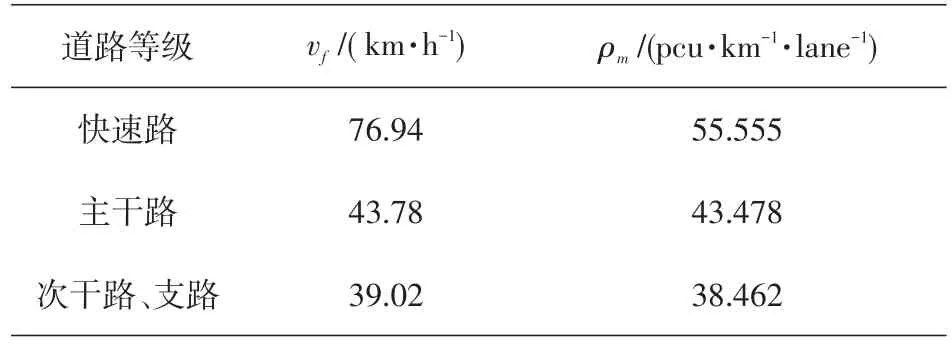
表3 北京市中心城区各等级道路速度—密度模型参数

表4 北京市中心城区各等级道路车道加权里程

北京市中心城区各等级路网承载力估计结果如表5所示。

表5 北京市路网承载力估计结果

结果显示，与低等级路网相比，高等级路网公路里程少、边界速度低、承载力强，将吸引更多的机动车出行需求，成为路网中供需矛盾突出的部分。高等级路网的自由流速度与边界速度差距大，运行动态范围大，宏观层面对需求变化更为敏感，拥堵的形成将更为迅速；同时由于边界速度低，拥堵一旦形成将更加严重，并且更难以消除，是监测与管理的重点。

5 结语

本文首次通过建立动态模型推算了城市路网瞬时所能承载的最大车辆数。由于使用路网运行大数据直接标定模型参数，推算结果与实际情况更为吻合。本文同时对比了不同等级道路网的承载力特性，为深入分析城市路网运行特性提供了新的研究思路。本文给出的方法可应用于多个领域。高等级道路更加快捷，低等级道路可达性更好，承载力估计结果有助于解决给定出行规模及出行特征条件下路网级配结构的评估及优化问题。将估计结果与机动车规模、出行特征、停车位数量相结合，有助于实现动静态交通一体化规划。将最大在途车辆数及对应的速度分别代入排放估计模型可估算瞬时机动车最大排放量。该方法只需根据社会浮动车数据即可完成建模，速度快，仿真效率高，适用于各类从整体路网中提取的子路网，具有较强的实用价值。

天气、路网规模、出行结构、出行空间及时间分布等条件的变化均会影响模型参数，进而影响估计结果。因此，建议在应用本文的计算方法时，可逐天分别标定模型参数，采用Monte Carlo法回归以获得长期性估计结果。