微分求积法在工程结构动力学中的应用研究

王冬梅，张 伟，刘寅立

(1. 天津科技大学理学院，天津 300457；2. 北京工业大学机电学院，北京 100124)

随着科学技术的发展，现代工程结构，无论是航空航天还是动力工程都向大型、高速、大功率、高性能、高精度和轻结构的方向发展，使得结构动力学问题尤为突出和重要．在结构系统中存在的材料弹塑性、构建大变形等非线性因素，在产品的设计、结构的控制中都需要考虑．对这些问题进行分析的第一步就是建立一个与实际结构基本相似的理想分析模型．任何一个实际结构是一个连续系统，用偏微分方程才能够精确地描述动力学问题．如果能求得偏微分方程的解析解，也就得到了问题的精确解；但是只有极少数的偏微分方程能够得到精确解．客观事物是多种多样的，尤其工程技术中的问题更是如此．由于实际需要，必须寻求各种数值方法以获得问题的近似解．动力学偏微分方程(组)含有空间变量和时间变量．数值求解含有空间变量和时间变量的偏微分方程(组)的近似解一般有空间离散和时间离散两个步骤．对方程空间离散后，产生一组关于时间变量的常微分方程，然后利用时间离散方法求解常微分方程组．常用的空间离散方法有有限差分法、加权残值法、伽辽金(Galerkin)法、有限元法、谱方法等[1–4]．

有限差分法是发展最早、比较成熟且应用最为广泛的求解偏微分方程的一种数值计算方法．有限差分法的数学基本原理是泰勒展开．任何差分格式都可以利用泰勒展开得到[5]．必须注意的是，对于内部点和边界点、均匀网格和不均匀网格，差分格式的表达是不一样的．比如，对于内部点，可以用中心差分格式，而边界点只能用向前差分或向后差分格式；对于非均匀网格点，差分格式的表达式非常复杂，尤其是高阶差分格式．由于以上特点，差分格式在实际应用中仅限于低阶的和均匀网格点．然而，对实际应用中许多问题的模拟常常需要非均匀网格和高阶差分格式．另外，低阶差分格式在求解问题时为达到所需精度，需要大量的网格点，这无疑会增大计算量．

20世纪 70年代初发展起来的微分求积法(differential quadure method，简称 DQ 法)则是一种高精度、易于实施的求解偏微分方程(组)的数值方法．微分求积法是于 1971年由美国学者 Bellman和Casti[6]作为对积分求积思想的推广而提出来的，其本质是将函数在求解区域内的每个网格处的导数值用域内全部网格点上的函数值的加权线性和近似表示．由于微分求积法相对于传统的数值计算方法具有原理简单(不依赖于变分原理)、计算量小、精度高、易于编程等优点，Bert等[7]于1987年首先将该法用于结构元件的分析，从而掀起了对微分求积法及其在工程应用中的研究热潮．2008年，Malekzadeh等[8]用微分求积法研究了叠层厚圆拱的面内自由振动．2009年，Matbuly等[9]用微分求积法对功能梯度裂缝梁的自由振动进行分析，计算了其固有频率．同年，刘金堂等[10]利用微分求积法对受面内载荷轴向运动板的横向振动进行分析，研究了轴向运动速度、板材料刚度及长宽比对板横向振动固有频率及临界速度的影响．2010年，Alibeigloo等[11]利用微分求积法对功能梯度圆柱壳进行了静力分析；2011年，Setoodeh等[12]利用微分求积法对功能梯度轴对称圆柱壳的瞬态动力学性质进行了分析．2012年，Jam等[13]对中等厚度的功能梯度板进行了非线性弯曲分析．2013年，Wang等[14]利用微分求积法研究了自由边界条件下的菱形板的自由振动．2015年，Tornabene等[15]利用微分求积法研究了复合椭圆及椭圆柱的自由振动．2017年，Arani等[16]利用微分求积法对碳纳米管电流变的夹层板的自由振动进行了分析．

截至目前，国内外学者将微分求积法用于动力学问题的研究还很少．以上微分求积法的发展和应用都是针对各种工程结构的静力、稳定性和自由振动分析，求解的方程是只含有空间变量的偏微分方程．本文将从理论上证明微分求积法是具有最高精度的高阶差分法，是低阶差分法的推广，精度高，计算量小，并且其权系数可以求出显示表达式，容易编制程序．从理论上把微分求积法推广到动力学偏微分方程的求解，为动力学问题的研究提供一种简单有效的分析方法．

1 微分求积法基本原理及其权系数的确定

1.1 微分求积法的基本原理

微分求积法的基本原理是将函数在求解区域内的每个网格点处的导数值用域内全部网格点上的函数值的加权线性和近似表示．简单起见，以一维函数为例说明DQ法的基本思想．

设函数 ()f x在区间[,]a b上有m阶导数．将区间[,]a b用N个点分成 1N−个区间，如图1所示．

图1 一维问题节点分布Fig. 1 One dimensional problem node distribution

则函数 ()f x在各节点处的各阶导数值表示为

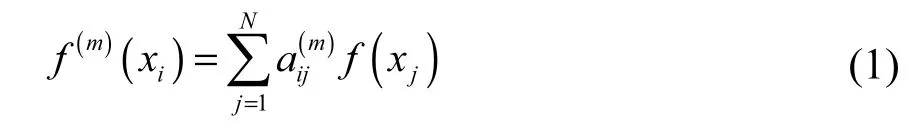
即

1.2 权系数的确定

在微分求积法发展的初期，其权系数矩阵均采用范德蒙矩阵求逆得到[6–7]．实践表明，在节点数大于15时对应的范德蒙矩阵是病态的，难以精确求出其逆矩阵，所以在运用中一般节点数小于15．为了克服DQ法在计算权系数时的困难，Shu等[17]提出广义微分求积法(generalized differential quadrature)，即通过对多项式线性向量空间的分析，利用拉格朗日插值多项式求导得出微分求积法权系数的显式表达式．微分求积法权系数的确定方法如下：

首先假定一个偏微分方程的解函数可以用高次多项式来近似．可以选用不同的多项式的基来表达函数 f( x)，比如选用基可以近似

表示为

若选用拉格朗日插值多项式基

其中

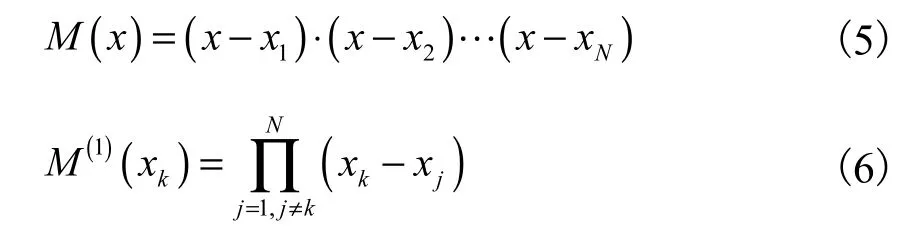
f( x)还可以用牛顿插值多项式、勒让德多项式近似．

则有

将式(9)代入式(8)得

下面采用拉格朗日插值多项式基或式(7)确定权系数．为了叙述的简明，令

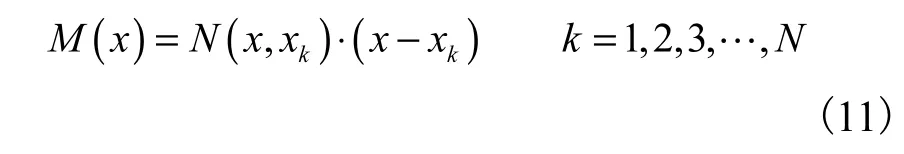
从表达式(13)中可以看出，如果给定 xi，由式(8)就很容易计算出，进而计算出，i≠j．但是，计算需要先求出二阶导数．这是一项非常复杂的工作．根据线性向量空间理论：多项式的一组基可以唯一地由另外一组基来表达．因此，如果一组基满足一个线性约束关系，比如式(1)，则另外一组基也满足此关系．因此，由拉格朗日插值多项式确定的与多项式基确定的是相等的．因此满足由多项式基时得到的关系式

式(7)两端分别对 x求二阶及高阶导数，并利用式(13)就得到高阶导数的权系数显式的表达式

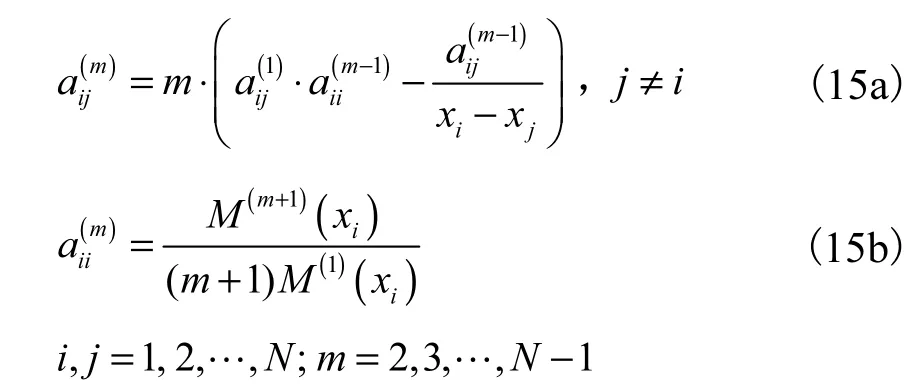
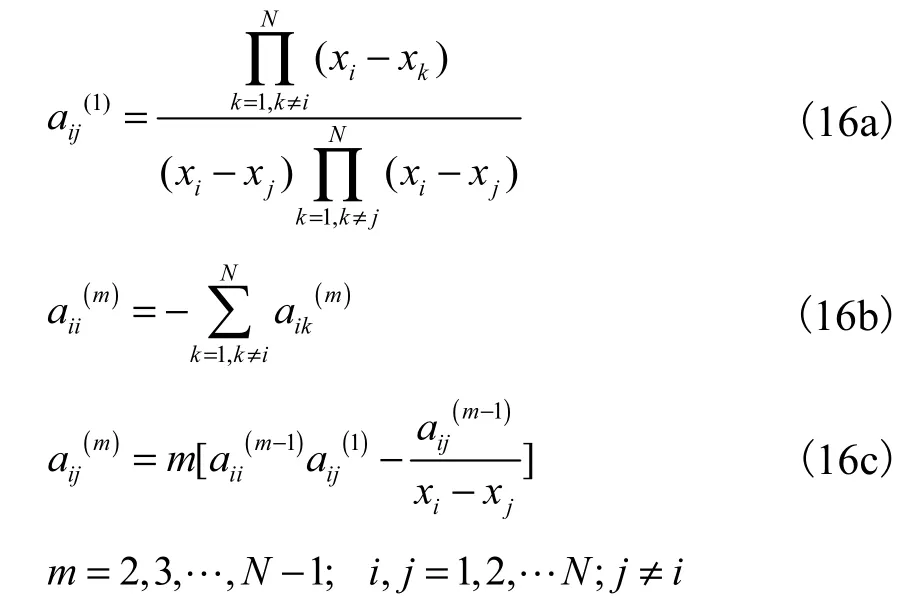
2 有限差分法的基本思想及差分格式的推导

一般使用的差分格式都是低阶的[5]，即给定网格点的各阶导数用一些邻近点的函数值的加权和来表示，其系数由泰勒展式得到．以一维函数为例，对于m阶导数，N个网格点可以产生−Nm阶精度的差分近似，如果在整个求解区域上只有N个网格点，那么对于m阶导数，−Nm阶差分格式应是最高精度的差分近似．1−N阶差分格式是最高精度的差分近似，比如，设

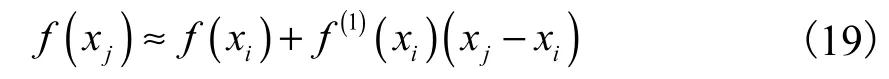
将式(18)代入式(17)得到

将式(18)代入式(1)可得到高阶导数的最高精度的高阶差分格式权系数满足的代数方程组

要得出高精度的高阶差分格式，需要求解式(22)代数方程组，当阶数较高时，其求解是非常困难的．

3 微分求积法和最高精度有限差分法的等价性

为说明微分求积法和最高精度有限差分法的等价性．首先需满足式(10)和式(21)方程组是等价的．显然它们的第一个方程是等价的，即

第二个方程也是等价的，即

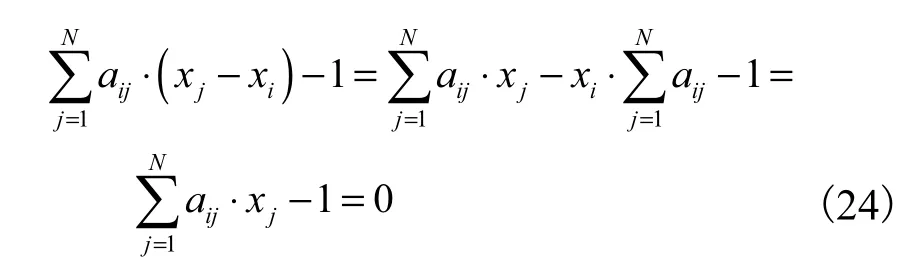
假设这两个系统的前1p+个方程都是等价的，即

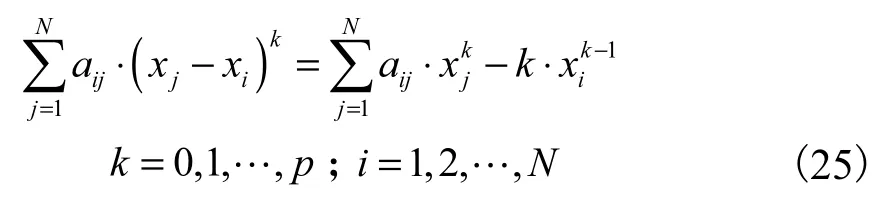
利用二项展开式

令1==ab，可以得到

利用式(26)，方程组(21)的前2p+ 个方程可以写为

将式(25)、式(27)代入式(28)得

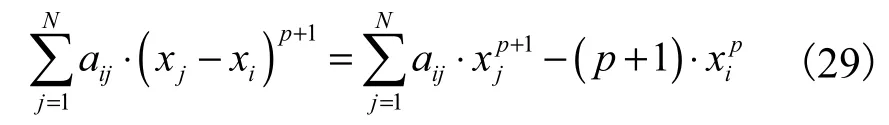
式(29)说明两个系统的第2+p个方程也是等价的．因此，式(10)系统和式(21)系统是等价的．

下面证明式(16b)和式(16c)与式(22)方程组是等价的．显然，式(16b)与式(22)的第一个方程是完全一样的．下面证明满足式(22)方程组．假设满足式(22)，即

将式(31)代入式(22)得

由此证明了式(16b)和式(16c)与式(22)方程组的等价性．

综上所述，微分求积法实质上是最高精度的有限差分法．

4 微分求积法应用于动力学偏微分方程

由前面讨论可知微分求积法(DQ)与最高精度的高阶差分法是等价的．高阶差分格式具有高阶截断误差，用高阶差分格式求解问题时只需要较少的网格点就能达到所需精度，而且无论是求解区域的内部点还是边界点，其差分格式的表达形式是一样的，因而高阶差分法的实施要比低阶差分法的实施容易．然而，用泰勒展开确定高阶差分格式的权系数需要求解代数方程组，这一工作非常复杂，而微分求积法的权系数已给出显式表达式，因此，解决实际问题时微分求积法则更易于实施．本节将微分求积法推广到动力学偏微分方程的求解．

4.1 求解原理

设某一动力学问题的控制方程及边界条件为

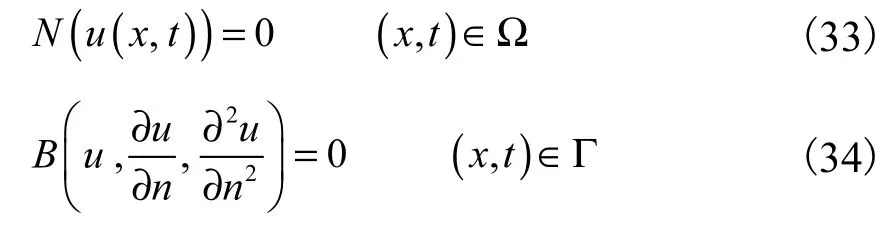
式中：N是一线性或非线性微分算子；u( x, t)是未知函数；B是一边界算子；Γ是区域Ω的边界；x和t分别是独立的空间变量和时间变量．考虑用微分求积法对其进行空间离散，以一维函数为例，设式(33)方程的解函数的空间变量x的变化范围是[a, b]，取N个互异节点

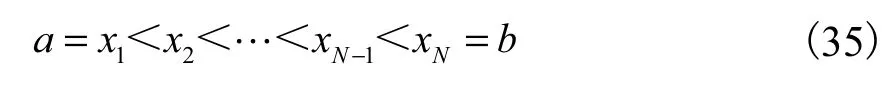
用矩阵形式表示为

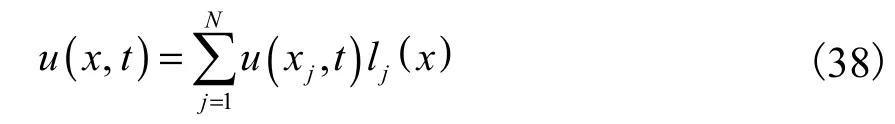
4.2 具体步骤

工程结构中的动力学方程大都是四阶及四阶以上的高阶偏微分方程．一个端点不止一个边界条件，因此边界条件的处理不能简单进行．下面用示例进一步说明微分求积法求解动力学方程的步骤、边界条件的处理方法以及微分求积法的计算量小、易于实施、高精度等特点．

例1 一受简谐作用力的简支梁的控制方程为

式中：EI是抗弯刚度；ρ是梁的密度；A为截面积；l为梁的长度；sinωPt为简谐激励．边界条件为

例 2 由 Wickert等[18]给出的一线性轴向移动梁的控制方程为

式中：u( x, t)为梁振动的横向位移；v为轴向移动速度；P为轴向紧力．边界条件同例1．

(1)数值离散

假设梁的长度为 1,m，则上述问题的求解区间为[0,1]．在区间[0,1]取N个互异节点实例中N=11，微分求积法常取切比雪夫多项式的根作为节点坐标

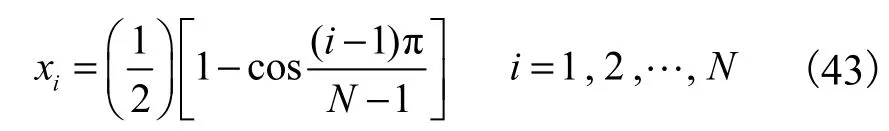
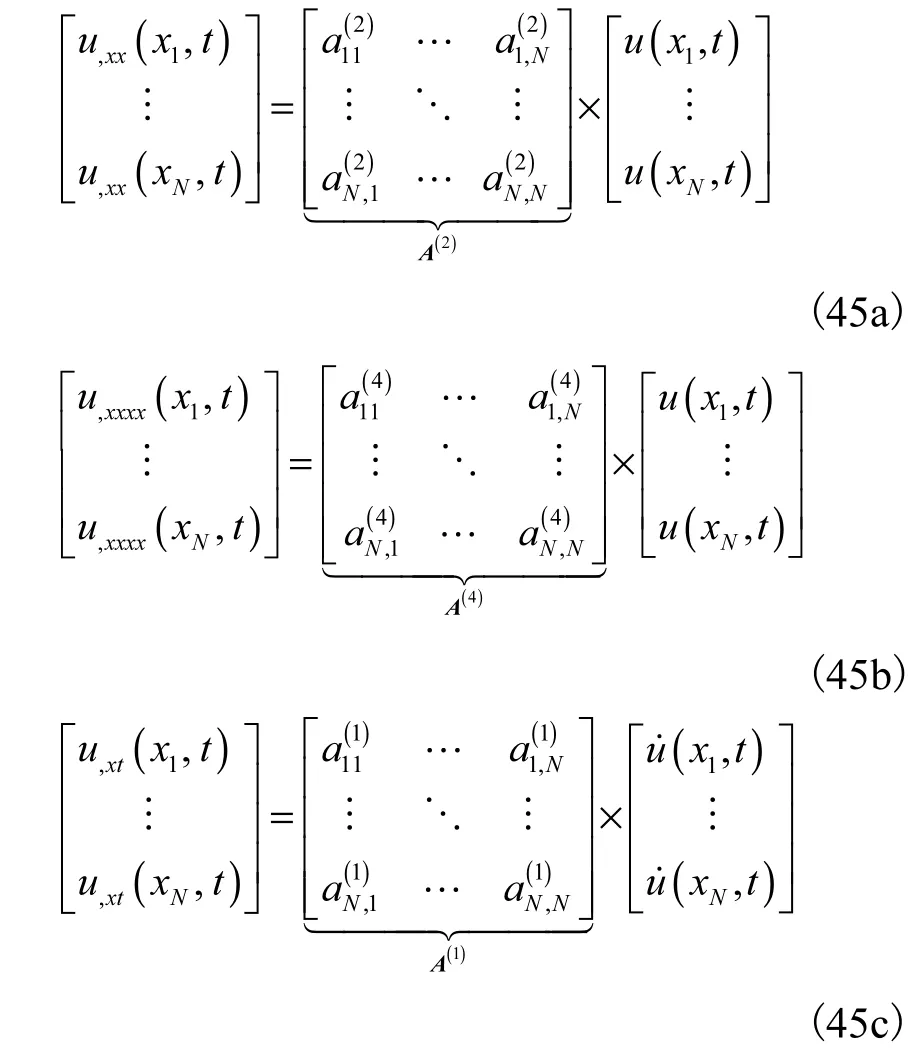
利用微分求积法则，方程中的未知函数在各节点处的各阶导数值表示为

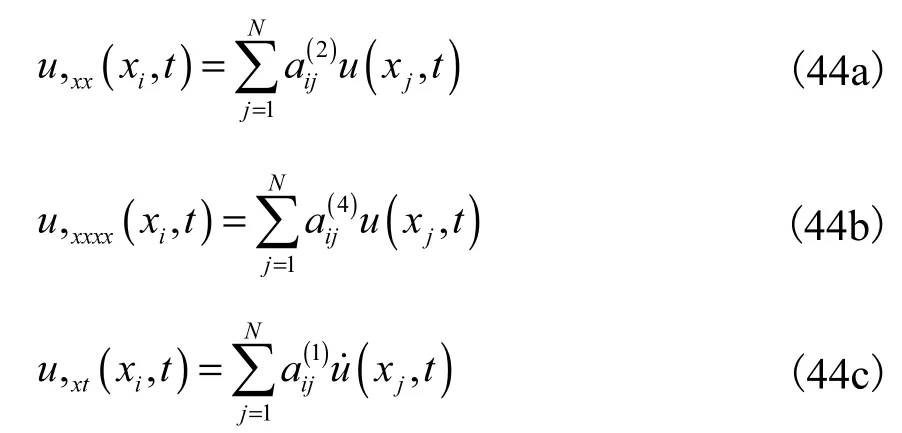
(2)处理边界条件

在计算四阶权系数矩阵时，应用矩阵乘积得

将式(48)分别代入控制方程(40)和(42)得

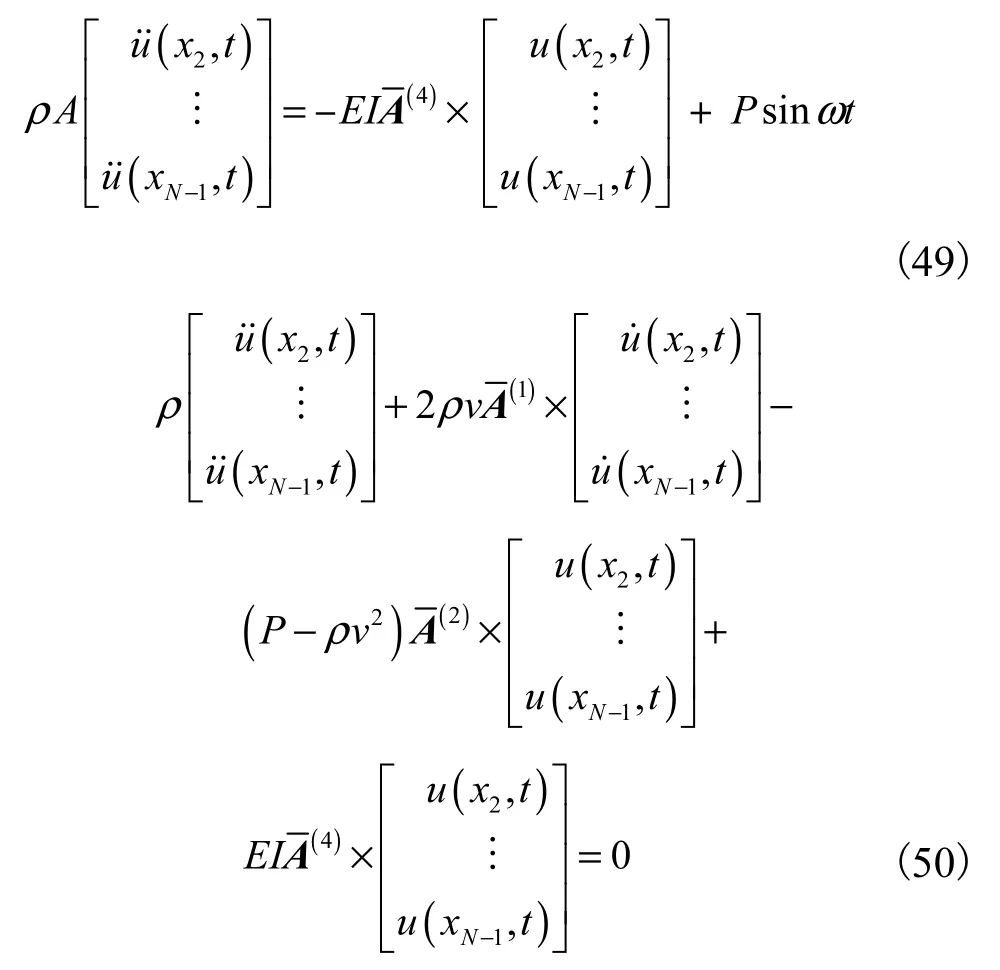
式(49)和式(50)都是二阶常微分方程组．

(3)求解常微分方程组

用时间离散方法如差分法、龙格库塔法求解式(49)和式(50)，即得梁横向振动的响应．如果是非线性的动力学方程，可以结合非线性动力学理论对工程结构进行周期、混沌、分叉等非线性动力学性质进行分析．

为了验证上述微分求积法的正确性和精确性，分别将上述两个示例的振动响应曲线的微分求积解和解析解作了比较，第一个例子的解析解可以用分离变量法[19]得到，第二个例子的解析解见文献[20]．图 2和 3分别描绘了系统(40)和(42)的梁横向振动的时间历程曲线．图 2中的参数取值为：图 3中的参数取值为：由图2和图3可以看出，微分求积解曲线和解析解曲线几乎是重合的，因而表明微分求积法是有效的，且只用 11个节点就达到较高的精度．

这两个示例中的边界条件是简支边界条件，用权系数矩阵修正法处理的边界条件，即在形成高阶权系数矩阵时就引入了边界条件．当然也可以用文献所述的δ法来处理，相比较就不如权系数矩阵修正法方便．只要边界条件中有低阶导数为 0，那么就可用权系数矩阵修正法处理，让此边界条件精确满足．

图2 式(40)系统的时间历程曲线Fig. 2 Time history curve of system(40)

图3 式(42)系统的时间历程曲线Fig. 3 Time history curve of system(42)

5 结 语

本文从理论上证明了微分求积法和最高精度的高阶有限差分法的等价性．高阶差分格式具有高阶截断误差，用高阶差分格式求解问题时只需要较少的网格点就能达到所需精度，而且无论是求解区域的内部点还是边界点，其差分格式的表达形式是一样的，因而高阶差分法的实施要比低阶差分法的实施容易．然而，用泰勒展开确定高阶差分格式的权系数，需要求解代数方程组，非常复杂，而微分求积法的权系数已给出显式表达式，因此，实际应用时利用微分求积法更易于实施．进一步地将微分求积法推广到动力学偏微分方程的求解，用数值算例阐明了微分求积法求解工程结构动力学偏微分方程的方法步骤，并将微分求积解与解析解进行比较，证明了微分求积法的有效性．以上研究结果表明了微分求积法具有高精度、易于实施、计算量小等优点，为工程结构的动力学分析提供了一种简单有效的方法．

［1］ 李荣华，冯国忱. 微分方程数值解法[M]. 北京：高等教育出版社，2002.

［2］ Morton K W，Mayer D F. 偏微分方程数值解法[M].李治平，门大力，许现民，等译. 北京：人民邮电出版社，2006.

［3］ 邱吉宝. 加权残值法的理论与应用[M]. 北京：宇航出版社，1991.

［4］ 向新民. 谱方法的数值分析[M]. 北京：科学出版社，2000.

［5］ 张文生. 科学计算中的偏微分方程有限差分法[M].北京：高等教育出版社，2006：40–55.

［6］ Bellman R E，Casti J. Differential quadrature and longterm integration[J]. Journal of Mathematical Analysis and Applications，1971，34(2)：235–238.

［7］ Bert C W，Jang S K，Striz A J. New methods for analyzing vibration of structural components[C]//Proceedings of the 28th Structures，Structural Dynamics and Materials Conference. Reston，VA：AIAA，1987：936–943.

［8］ Malekzadeh P，Setoodeh A R，Barmshouri E. A hybrid layerwise and differential quadrature method for in-plane free vibration of laminated thick circular arches[J]. Journal of Sound and Vibration，2008，315(1)：212–225.

［9］ Matbuly M S，Ragb O，Nassar M. Natural frequencies of a functionally graded cracked beam using the differential quadrature method[J]. Applied Mathematics and Computation，2009，215(6)：2307–2316.

［10］ 刘金堂，杨晓东，闻邦椿. 基于微分求积法的轴向运动板的横向振动分析[J]. 振动与冲击，2009，28(3)：178–181.

［11］ Alibeigloo A，Nouri V. Static analysis of functionally graded cylindrical shell with piezoelectric layers using differential quadrature method[J]. Composite Structures，2010，92(8)：1775–1785.

［12］ Setoodeh A R，Tahani M，Selahi E. Hybrid layerwisedifferential quadrature transient dynamic analysis of functionally graded axisymmetric cylindrical shells subjected to dynamic pressure[J]. Composite Structures，2011，93(11)：2663–2670.

［13］ Jam J E，Maleki S，Andakhshideh A. Non-linear bending analysis of moderately thick functionally graded plates using generalized differential quadrature method[J]. International Journal of Aerospace Sciences，2012，1(3)：49–56.

［14］ Wang X W，Wu Z. Differential quadrature analysis of free vibration of rhombic plates with free edges[J]. Applied Mathematics and Computation，2013，225：171–183.

［15］ Tornabene F，Fantuzzi N，Bacciocchi M，et al. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method[J]. Thin-Walled Structures，2015，97：114–129.

［16］ Arani A G，Jamali S A，Zarei H B A. Differential quadrature method for vibration analysis of electro-rheological sandwich plate with CNT reinforced nanocomposite facesheets subjected to electric field[J]. Composite Structures，2017，180：211–220.

［17］ Shu C，Richards B E. Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations[J]. International Journal for Numerical Methods in Fluids，1992，15(7)：791–798.

［18］ Wickert J A，Mote C D. Response and discretization methods for axially moving materials[J]. Applied Mechanics Reviews，1991，44(11S)：279–284.

［19］ 郑兆昌. 机械振动[M]. 北京：机械工业出版社，1980.

［20］ Kong L，Parker R G. Approximate eigensolutions of axially moving beams with small flexural stiffness[J]. Journal of Sound and Vibration，2004，276(1)：459–469.