液浮惯性仪表温度场的仿真分析

刘毕炎，严小军，王 昕

（北京航天控制仪器研究所，北京100039）

0 引言

液浮惯性仪表的温度梯度及温度波动直接影响浮子的重浮力残差、浮油扰动力矩波动以及浮油参数的稳定性，从而产生附加力矩或剪切应力，影响仪表精度。由于三浮陀螺加速度计内部结构复杂，传热途径、边界条件等关键参数难以精确确定，一般都是通过初步的理论分析和简单的试验方法来对仪表进行热设计，这种方法缺乏对仪表详细的温度分析，无法获取仪表内部温度场的分布状态［1-2］。本文使用有限元方法，对液浮惯性仪表的温度场进行分析，得到了仪表内部的温度场分布，为仪表的热设计提供基础参数，从而为降低仪表内部温度梯度和仪表的温度系数打下基础［3］。

1 液浮惯性仪表的结构组成与传热途径

液浮惯性仪表主要由壳体、变磁阻传感器、无刷力矩电机、陀螺摆组件、输电装置5部分组成，具体结构如图1所示［1-2］。马达是内部热源，其输入功率大部分转化为热量，通过对流和传导的方式传递到浮筒内壁，浮筒再将这些热量传给浮油。3个加热片采用带状薄膜加热片，分别缠绕在液浮惯性仪表的内壳体和大端盖上，它的热量通过热传导传到内壳体上，内壳体再将这些热量传到浮油。陀螺摆组件的热量一部分通过壳体内的空气以对流换热的方式传导到壳体上，另外一部分通过下轴和输电装置以热传导的方式向外传热，液浮惯性仪表的主要传热途径如图2所示。

2 温度对液浮惯性仪表精度影响的分析

仪表内部温度变化和温度分布不均匀会对高精度惯性仪表性能造成极不利的影响，从而直接影响惯性仪表的精度［4-5］。对于液浮惯性仪表而言，浮子内部发热和传热不均匀能使浮油温度不同而发生密度不均匀现象。浮油密度的变化会使浮力大小改变，破坏浮子正常的平衡状态，产生的干扰力矩将直接影响液浮惯性仪表的精度，下面对浮油径向温度梯度对仪表精度的影响进行分析。

假设浮子为规则的圆柱体，浮子径向截面图如图3所示。理想情况下，浮子的质心调整在OY轴上，假设浮子的长度为L，半径为R，体积为V0，X轴方向上所受比力为aX，M为浮油径向温度梯度引起的干扰力矩，ml为内框架的摆性值。设浮子左端对应的浮油的温度和密度为T1、ρ1，浮子右端对应的浮油的温度和密度为T2、ρ2，设浮油的密度随温度增大而减小，且密度反比于温度，T1＜T2，ρ1＞ρ2。 这样形成浮子左半边的浮力大于右半边，使质心从O点向-Z方向移动［1-2］。

设平行于OXY平面切割浮子一薄片，如图3所示，该薄片位置的液体密度为：

该薄片体积为：

浮油对该薄片浮力为：

作用在Y轴的力矩为：

假设浮油密度与温度值成反比，浮油密度与Z坐标之间的函数关系为：

浮子整体受到的干扰力矩为：

引起角速度误差：

折合成相对误差：

3 温度场有限元仿真分析

3.1 有限元理论基础

根据Laplace方程，在一般的三维问题中，瞬态温度场的场变量T（x，y，z，t）在直角坐标中应满足的微分方程为［7］：

T（x，y，z，t）是不同时间和不同坐标轴对应的温度值；ρ是材料密度；c是材料比热容；λx、λy、λz是材料沿物体 3 个方向（x，y，z）的导热系数；Q＝Q（x，y，z，t）是物体内部热源密度；nx、ny、nz是边界外法线的方向余弦；T＝T0是在Γ1边界上给定的温度；q＝q0是在Γ2边界上给定的热流密度，h是对流换热系数；对于Γ3的边界，在自然对流条件下Tw是外界环境温度。

由泛函变分原理求式（13），即可以求得所有节点温度，这就是有限元求解温度场的基本思想。

3.2 三维模型的建立

对液浮惯性仪表进行有限元仿真，首先要建立三维模型，通过设置合理的边界条件，才能进行仿真分析。液浮惯性仪表结构复杂，简化计算模型是必要的［7］。既要保证计算模型与真实模型在结构、尺寸上的一致性，又要保证模型的计算效率，简化后的液浮惯性仪表共有44个零件，简化后的三维几何模型如图4所示。

3.3 边界条件的确定

液浮惯性仪表正常工作情况下主要发热元件有6个：马达、大加热片、小加热片（2个）、变磁阻传感器和力矩电机。具体分布位置和稳态热载荷如表1所示。

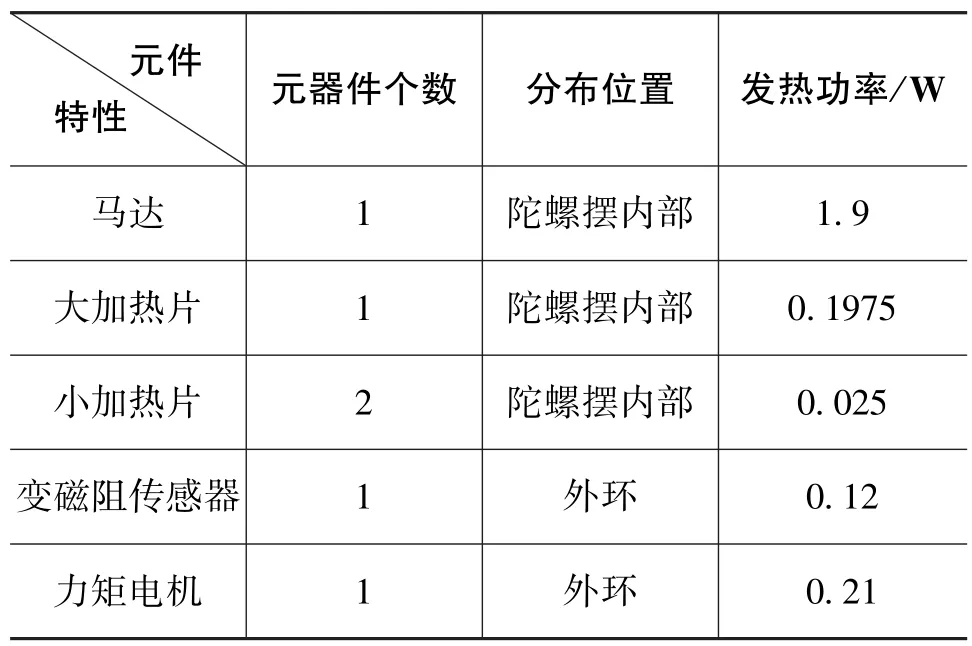
表1 液浮惯性仪表稳态热载荷Table 1 Power dissipation of LFII

液浮惯性仪表有两级温控：外温控为仪表提供55℃的环境温度，减小外界温度对仪表的影响，提高控温精度；在仪表启动阶段，内温控给仪表加热到工作温度点66℃±2℃，实现高精度温度补偿、平衡。为了模拟真实的传热情况，环境温度温度取55℃；对流换热系数取10W／（m2·℃）。

液浮惯性仪表正常工作并稳定后，内部陀螺的马达转子高速旋转，相对于氦气具有较高的相对速度，使马达转子和氦气之间产生强迫对流换热。当液浮惯性仪表沿输入轴有加速度时，陀螺摆组件会绕外环轴产生进动，壳体内部的空气会发生流动，空气会在陀螺摆组件和壳体之间产生对流换热。由于氦气和空气都分别密封于浮筒内部和壳体内部，能量散失很少。本文将这类气体的对流换热当作气体的热传导来计算，导热系数采用当量导热系数［6］。主要材料的热物理特性如表 2 所示［7］。

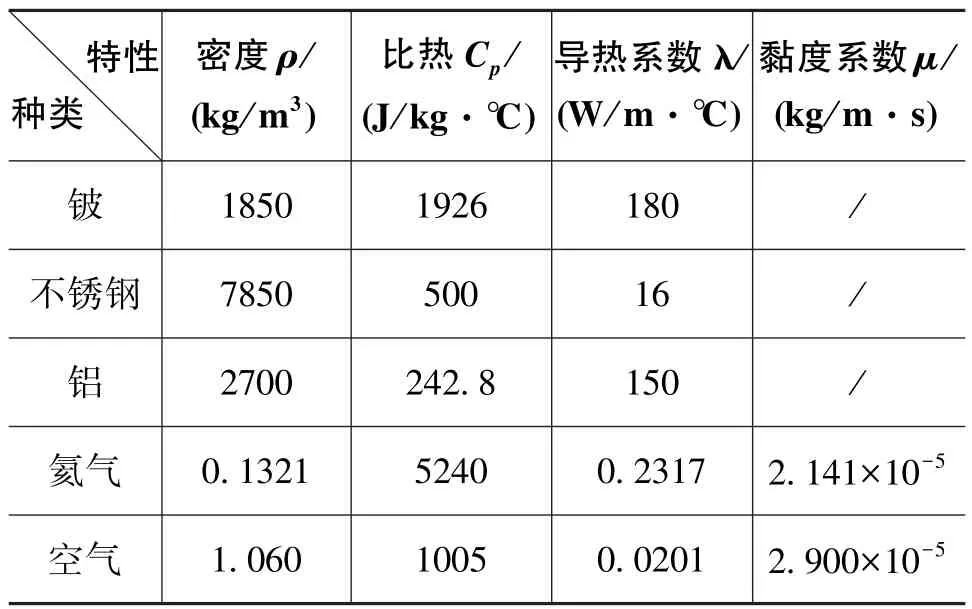
表2 主要材料的热物理特性Table 2 Heat physical properties of main material

根据经验公式计算氦气和空气的当量导热系数。

Nusselt数为：

Reynolds数为：

Prandtl数为：

经计算：氦气的特征速度u1＝26.37m／s，外环空气的特征速度u2＝0.03768m／s。

根据式（14）～式（16）， 可求得：

氦气当量系数λe＝Nμλ＝4.47W／（m·°C）

空气当量系数λe＝Nμλ＝0.10W／（m·°C）

3.4 仿真结果的分析

对模型进行网格划分，划分单元采用四面体单元为主，六面体单元为辅的方法，划分后的网格单元数为4.4×105，划分结果如图5所示。

除给予适当的镇静治疗外，还要有一个舒适的睡眠环境。不要反复搬动宝宝，避免惊吓，防止因宝宝抵抗力差而继发细菌感染。安置在阳光充足的房间，保持室内整洁，室温保持在18～22℃，湿度50%～60%，空气要新鲜，定时开窗通风换气，使空气流动和清洁，保持房间安静。房间内不放置花草，尽可能避免加重喘息发作。

对模型施加边界条件进行仿真，仿真结果如图6所示。

从图6可以看出，液浮惯性仪表的最高温度为73.52℃，位于马达处；最低温度为57.84℃，位于上罩外侧。氦气的温度分布为67.22℃～73.47℃，温度梯度为6.25℃，因为氦气主要靠强制对流进行换热，所以热阻较大。浮油整体的温度分布为66.62℃～68.06℃，温度梯度为1.44℃。靠近轴向磁悬浮磁片位置浮油的温度最高为68.06℃，马达的热量主要通过马达支架散出，磁悬浮磁片直接粘接在支架上距离马达最近的位置，使此处浮油的温度最高。波纹管处浮油温度最低为66.62℃，这是因为波纹管与空气直接接触，加快了散热，使此处浮油温度最低。如果只考虑浮筒周向的浮油，浮油的温度分布为66.95℃～67.17℃，仿真结果显示浮油最大径向温度梯度为0.07℃，造成的误差小于1.4×10-7，能够满足当前仪表的精度要求。

4 试验验证

要得到仪表内部温度场真实的分布情况，应尽可能选择较多的测温点。由于液浮惯性仪表体积小、结构复杂，采用热敏电阻测温法采集仪表内部温度信息，如图7所示。整个液浮惯性仪表共选取9个测温点，外环4个，陀螺摆组件5个。为了避免正常工作时热敏电阻引线对陀螺摆组件进动产生影响，陀螺摆处的热敏电阻（R1～R5）和下轴的热敏电阻（R6）都通过输电装置引出，然后连接到测试设备上，其他热敏电阻直接连接到测试设备上。热敏电阻具体分布位置如图7所示，大护线板1个（R1）， 内壳体 4 个（R2～R5）， 下轴 1 个（R6）， 壳体 2个（R7、R8）， 电机壳体 1 个（R9）。

按照正常工艺流程对试验表进行两次试验，用多通道数据采集系统KEITHLEY 2700同时监测9个热敏电阻阻值的变化。待仪表温度稳定，提取热敏电阻的阻值并换算成温度值，各特征点的温度值数据如表3所示。

表3 试验数据表Table 3 Experimental data

由表3可以看出：

1）R1为测温电阻，分布在大护线板外侧，直接显示大护线板端的浮油温度。试验结果显示R1温度为66.51℃，这与试验表温度点66.5℃是吻合的。

3）R7、R8、R9受外温控影响较大，外温控使液浮惯性仪表的环境温度保持在55℃左右，液浮惯性仪表外表面的温度比外温控温度高3.5℃左右。

提取特征点仿真结果，与试验数据对比，仿真试验对比如表4和图8所示。

表4 仿真试验数据对比表Table 4 Contrast data of experiment compared with simulation

对比仿真和试验的结果可知：

1）仿真的结果与试验的结果趋势基本吻合，证明了仿真结果的正确性；

2）仿真值比试验值偏高，主要是模型的简化、材料的选取、热阻的设置等原因造成的，需要进一步修正仿真的参数。

5 结论

针对仿真和试验结果，可以得到如下结论：

1）浮油最大径向温度梯度为0.07℃，造成的误差小于1.4×10-7，当前仪表的精度为1×10-6，能够满足精度要求。但如果需要进一步提高仪表精度，则需要减小浮油径向温度梯度。可以选择密度、黏度对温度曲线相对平稳的浮油，当出现温度梯度时，密度和黏度的变化不大，对仪表精度影响也会小些。

2）大护线板端（R2）浮油温度比小护线板端（R4）浮油温度低0.2℃左右，主要是因为大护线板端散热面积较大引起两端散热不均。两端温差会造成浮油流动，从而产生附加力矩或剪切应力，可以通过提高大护线板端加热片的功率来减小两端温差。

3）氦气主要通过强制对流换热使马达与外界进行热交换，马达内部氦气的温度梯度为6℃左右，增大氦气压力、提高马达转速可以减小氦气热阻，加快氦气的散热。

本文首先说明了液浮惯性仪表温度场研究的必要性，通过建立液浮惯性仪表的数值模型，用有限元软件进行仿真计算，得到了整表的温度场分布，并通过试验验证了仿真结果的正确性，为降低仪表内部温度梯度和提升仪表的精度等级提供了参考。

［1］ 陆元九.惯性器件 （上） ［M］.北京:中国宇航出版社，1990.LU Yuan-jiu.Inertial devices （1st） ［M］.Beijing:China Aerospace Press，1990.

［2］ 陆元九.惯性器件 （下） ［M］.北京:中国宇航出版社，1990.LU Yuan-jiu.Inertial devices （2nd） ［M］.Beijing:China Aerospace Press，1990.

［3］陈贵明，刘小方，刘鲭洁，等.液浮陀螺仪性能改进技术［M］.北京:科学出版社，2014.CHEN Gui-min，LIU Xiao-fang，LIU Qing-jie，et al.Property improvement of bearing gyroscope ［M］.Beijing:Science Press，2014.

［4］ 张沛勇，邓忠武.三浮陀螺温度场数值分析［J］.导航与控制，2008，7（4）:20-24.ZHANG Pei-yong，DENG Zhong-wu.Temperature field analysis on the threefold floated gyro ［J］.Navigation and Control，2008，7（4）:20-24.

［5］卜石，刘娜.利用AWE分析三浮陀螺浮子结构温度场［J］.弹箭与制导学报，2005，25（4）:966-968+977.BU Shi，LIU Na.Temperature field analysis on a type of floated gyro floater structure by using AWE software ［J］.Journal of Projectiles，Rocket Missiles and Guidance，2005，25（4）:966-968+977.

［6］郑云霞，陈东生，唐文林.单自由度静压液浮陀螺仪温度场的分析与研究［J］.导航与控制，2005，4（2）:29-35.ZHENG Yun-xia， CHEN Dong-sheng， TANG Wenling.The analysis and study on node temperature of the single freedom hydro-static bearing gyroscope ［J］.Navigation and Control，2005，4（2）:29-35.

［7］ 杨世铭，陶文铨 .传热学［M］.北京:高等教育出版社，2006.YANG Shi-ming，TAO Wen-quan.Heat transfer theory［M］.Beijing:Higher Education Press ，2006.